考慮縱向滑移的組合梁隨機有限元可靠度分析

賈布裕, 余曉琳, 顏全勝

(華南理工大學 土木與交通學院, 廣東 廣州 510640)

考慮縱向滑移的組合梁隨機有限元可靠度分析

賈布裕, 余曉琳, 顏全勝

(華南理工大學 土木與交通學院, 廣東 廣州 510640)

摘要：針對鋼-混組合梁構造復雜、材料多樣、不確定性強的特點,從隨機不確定性的角度來研究鋼-混組合梁，基于Newmark幾何模型,將鋼-混組合梁的混凝土板、鋼梁以及剪力連接件作為整體單元考慮,通過采用T.L列式增量法,提出并推導了考慮縱向滑移效應的非線性組合梁單元模型。結合直接微分法,對組合梁的結構響應梯度進行了計算分析；并由FORM法計算得到可靠度指標,對鋼-混組合梁算例進行了隨機有限元可靠度分析。計算結果表明：在實際工程中,并不需要完全剛性連接來保證結構的可靠性；在保證安全方面,考慮幾何非線性來計算結構的可靠度是有必要的。

關鍵詞：鋼-混組合梁；縱向滑移；非線性組合梁單元；直接微分法；隨機有限元；可靠度分析；幾何非線性

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20151104.1629.002.html

網絡出版日期：2015-11-04.

余曉琳(1978-), 女, 副教授.

近二三十年來,隨著鋼-混組合結構在工程領域的廣泛應用,學者們開展了各種關于鋼-混組合梁的研究工作,取得了豐富的成果,主要集中在以下幾個方面：非線性分析[1-2]、縱向滑移效應[3-7]、橋面板長期時變效應[8]、剪力連接件抗剪[9]以及有限元單元模擬[3 ,10]等。但以上的研究都局限于確定性的結構分析,對鋼-混組合結構的不確定性分析,如結構隨機性分析則鮮有人涉及。結構隨機性包括結構材料本身物理性質以及幾何特性的隨機不確定性和外界對其施加作用的隨機不確定性。鋼-混組合梁涉及多種材料,單元構造復雜,隨機不確定性因素較多,如何將鋼-混組合梁確定性結構的計算分析手段和用于分析隨機性的可靠度分析方法結合起來,對將鋼-混組合梁進行隨機有限元可靠度分析,是目前研究的難點之一。本文以推導的考慮縱向滑移效應的非線性組合梁單元模型為基礎,采用直接微分法,對鋼-混組合梁進行隨機有限元可靠度分析,并對數值算例進行了計算分析。

1有限元模型

1.1　幾何位移模式

如圖1所示的典型的鋼-混組合梁截面,頂板是混凝土橋面板,下托梁是工字鋼梁,兩者通過剪力連接件相連。圖中坐標x軸為順橋向,z軸為橫橋向,y軸為豎向。計算采用如下基本假定：

1) 橫截面對稱于yox平面；2) 不考慮組合梁的豎向掀起(即橋面板和鋼主梁的豎向撓度一致)；3) 忽略剪切變形影響；4) 剪力連接件沿梁均勻分布。

由于不考慮組合梁的豎向掀起影響,鋼主梁和橋面板的豎向撓度可用同一個豎向位移表示。

圖1　幾何模型以及單元位移示意圖Fig.1　Geometric model and element displacements

組合單元t時刻橋面板和鋼主梁截面上任一點的位移和位移增量可表示為

(1)

組合梁t時刻縱向滑移位移以及增量的表達式為

(2)

其中,h=ys-yc,值得注意的是,式(2)適合于描述幾何線性問題,但從工程實踐運用角度來看,橋面板和鋼主梁之間的滑移變形(比如轉動)被看作為是有限的,所以式(2)也適合用于描述組合梁幾何非線性的縱向滑移位移[5]。

1.2　單元模式

將組合梁沿軸向進行一維離散,單元模式并沒有采用常規的8自由度法(兩端節點各4自由度),因為若采取8自由度法,則u的形函數的插值為一次多項式,而v的形函數的插值為三次多項式(v′為二次), 就會發生“滑移鎖定”問題[3]。為避免此類問題的發生, 可采用增加內置自由度的方法。采取在單元內部u位移量增置2自由度的方法,最后得到了10自由度的單元模式(如圖2所示)。t時刻單元節點位移向量以及節點位移增量向量為

組合梁的位移場為{uc,us,v},則t時刻單元內的位移和增量通過形函數可表示為

其中,形函數N為

各個構件格林應變增量可表示為

(3)

由虛功原理結合基于T.L列式增量法得到平衡方程：

(4)

圖2　單元節點自由度示意圖Fig.2　Element nodal degrees of freedom

2組合梁結構隨機有限元分析

在有限元分析過程中,首先由控制方程中得到主要反應量,如單元節點位移反應量,在得到主要反應量后,單元應變或應力即可從主要反應量通過顯式的表達式得到,而主要反應量也是基本隨機變量的函數,所以可將基于隨機有限元的極限狀態方程G寫為主要反應量d和基本隨機變量θ的函數：

(5)

(6)

(7)

式中:K為切線剛度矩陣。由式(5)可得極限狀態方程函數G對基本變量θ的梯度計算公式：

(8)

接著計算標準正態空間極限狀態函數G(u)的梯度向量：

式中:Jθ,u表示Nataf分布對獨立標準正態分布的Jacobi矩陣,θg則由求得,其中的和可直接通過功能函數形式獲得,而可通過式(7)計算得到的結構主要反應量d對任一隨機參數θ的梯度值集合向量獲得。最后求得uG后,采用改進HL-RF迭代法,由FORM法計算得到一次可靠度指標β和設計試驗點u*。

為了避免“滑移鎖定”的發生,本文在單元內部增置了內部節點自由度,而在有限元求解過程中,需要通過靜力凝聚法將內部節點的抵抗內力集合到結構抵抗力。靜力凝聚法通常用于有內部節點的單元有限元求解,其目的是為了縮減有限元系統方程求解規模,根據靜力凝聚法,可知結構的控制平衡方程為

(9)

進行靜力凝聚法后式(9)可等效寫為

通過成功救治的案例，我們回顧本例的治療經過，復習相關文獻資料，我們認為，急性化膿性中耳炎A族鏈球菌感染合并顱內感染，需要多學科合作，由于患者多伴有基礎病，基礎病的治療應給以足夠重視；一旦出現顱內并發癥，應當及時行中耳乳突病灶的清除及術腔引流；抗感染治療聯合用藥，根據藥敏試驗，選擇敏感的，能透過血腦屏障及的抗生素，靜脈給藥，療程足夠。

(10)

(11)

式(11)兩邊對di求偏導 (固定隨機變量θ)：

(12)

將式(12)對隨機變量θ進行偏導,可得

(13)

同樣式(11)兩邊對隨機變量θ求偏導有

(14)

(15)

結合式(13)～(15),整理可得

(16)

假設整個單元處于彈性,而Pint為上文推導的單元內力,其表達式為

(17)

式中：BLc、BLs為格林應變增量的線性表示,BN為格林應變增量的非線性表示,Nf為滑移增量,式(17) 左右兩邊對隨機變量θ進行求偏導,最后整理可得

在此暫不考慮節點坐標的隨機性,只先考慮隨機變量θ為材料參數,按類似前節的推導方法,可得

式中：F(x,θ)為根據上文所推導的組合梁單元節點截面力,即

式中：fc(x,θ)為上層混凝土軸向力,fs(x,θ)為下層鋼主梁軸向力,Mcs(x,θ)為整個組合截面的彎矩,ω(x,θ)為連接件單位長度剪力,而以上各項需要通過截面積分得到,由于d固定條件等價于ε固定條件,則最后可以得到基于截面層次的梯度表達式：

上述兩式右邊項的條件求導以及連接件單位長度剪力ω(x,θ)的條件求導的計算需要借助于材料層次的梯度分析。材料應力對任一隨機變量θ進行偏導,可得

3數值算例分析

根據上述方法,采用C++語言以及Matlab程序,結合自編的組合梁確定性有限元程序編制了適用于組合結構的隨機有限元分析程序,并對2個組合梁算例進行了隨機有限元的可靠度計算分析。

3.1　簡支組合梁算例

如圖3所示的簡支組合梁,在上層構件上作用著均布荷載,并在上下2層中心沿縱向方向分別作用一對大小相等方向相反的集中力。上下2種材料均為線彈性,上層構件的彈模為12 GPa,下層構件的彈模為8 GPa,連接件的剛度通過定義一個無量綱剛度系數αL來表示：

式中：L為結構長度,k為連接件剛度,E1和E2、A1和A2、I1和I2分別為上下2種構件的彈模,面積以及截面慣性矩、h為沿截面高度上下2個構件質心之間的距離。選取上下2個構件的面積、慣性矩、彈模和連接件的連接剛度以及作用在上層結構的均布荷載作為隨機變量,隨機變量的特征如表1所示。

表1　隨機變量特征表Table 1　Characteristics of structural random variables

為了分析幾何非線性以及連接件剛度對可靠度的影響,對幾何線性、幾何非線性以及5種連接件剛度工況下的結構可靠度進行了計算分析,計算結果見表2和圖4。

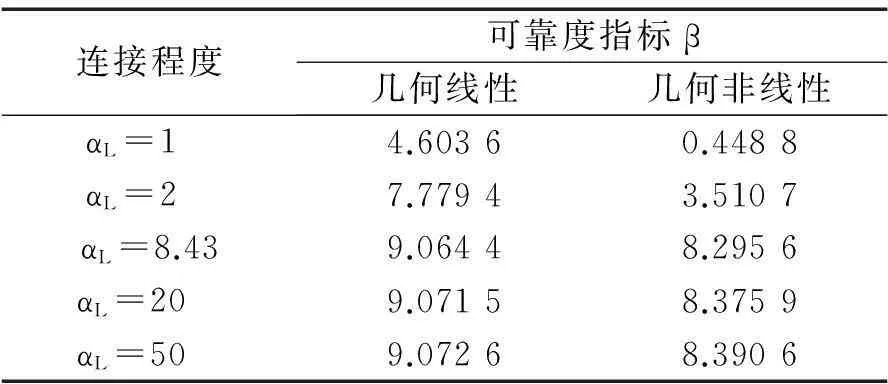
表2　多種工況下的可靠度結果.Table 2　Reliability results of different conditions

圖4　考慮幾何線性、非線性及不同連接剛度的可靠度結果Fig.4　Reliability results of geometric linear, non-linear and different connection stiffness

從表2以及圖4中可知：幾何線性工況下的可靠度明顯比幾何非線性工況下的可靠度高,所以在保證安全方面,考慮結構的幾何非線性來計算結構的可靠度是有必要的；無論是幾何線性還是幾何非線性,結構的可靠度隨著連接件剛度的變大而迅速增大,但當連接件的剛度達到一定數值時,連接件剛度的增加對結構可靠度的增加影響甚小,換言之,只要連接件的剛度達到一定程度,就可以保證達到和完全剛性連接組合結構基本一致的可靠度。所以在實際工程,并不需要完全剛性連接來保證結構的可靠性,相反可以通過計算得出一定的連接剛度來設計連接件,這樣可有效減少材料費用。

3.2　連續組合梁算例

如圖5所示,該結構為一根兩跨組合連續梁,組合梁上部構件為一塊混凝土板,下部構件為一塊工字鋼,兩者通過連接件聯結在一起,各跨的跨中各作用豎向集中力P。材料為非線性,各構件的材料本構關系見圖5。考慮材料本構參數以及單跨跨中豎向集中荷載P的隨機性,對結構進行了可靠度分析,隨機變量特征見表3。單元劃分數為14,設所有單元的fc1、εc1、fc2、εc2、fc4、εc4、fs、εsh、fmax、δh分別完全相關。功能函數定為：g=0.012-Δ (Δ為單跨跨中撓度)。

圖5　集中荷載作用下連續組合梁及材料本構關系Fig.5　The continuous composite beam with concentrated force, and material constitutive relationships of components

表3　隨機變量特征表Table 3　Characteristics of structural random variables

首先考慮無軸向壓力的工況,采用所提方法計算得到的可靠度指標為β= 3.890 6,失效概率為Pf=5.00×10-5。為了驗證結果的正確性,采用MC法,抽樣106次進行可靠度計算,MC法所得到的失效概率為Pf=1.00×10-5,可靠度指標β=4.264 9,其結果和所提方法結果比較吻合。對有軸向壓力的工況同樣進行了可靠度計算分析,軸向壓力P1仍然分別取為0、500、1 000、1 500 kN,其分別對應的可靠度結果如圖6所示。正如圖6所示,由于軸向壓力的作用,結構的撓度將增大,其對應的可靠度將隨之減小。

圖6　不同軸向壓力的可靠度結果Fig.6　Reliability results of different axial forces

4結論

1)組合梁結構構造復雜,不確定性程度高,因此采用隨機可靠度思想進行分析是非常有必要的；

2)首先建立了確定性的組合梁單元模型,能考慮縱向滑移效應和非線性影響,更加真實、準確地反映了組合梁的受力性能；

3)將基于直接微分法的隨機有限元法直接應用于所推導的非線性組合梁單元,得出了考慮縱向滑移效應的組合梁結構響應梯度表達式。在其基礎上編制的組合梁隨機有限元程序能有效完成對組合梁斜拉橋的隨機有限元分析；

4)所提的隨機有限元法直接以確定性有限元為基礎,相比目前較為流行的響應面法,在精度和穩定性方面具有獨特優勢(尤其是復雜或非線性程度較高的結構)；

5)算例結果表明：連接件的剛度對提升組合梁結構的可靠度具有重要影響,其隨著連接件的剛度變大而增大,但連接件的剛度達到一定界限值時,可靠度不再增大,因此設計時需注意到此點,無需過于保守,避免浪費；計算組合梁的可靠度時,應考慮幾何非線性的影響,考慮幾何非線性得到的結果和考慮幾何線性得到的結果存在明顯差異。幾何非線性降低了組合梁結構的可靠度值,這點在實際工程中需引起重視；

6)組合梁結構是一個復雜的組合體,其失效模式眾多,如還有抗彎極限、豎向抗剪極限等問題，今后還需完善這些方面的可靠度研究。

參考文獻：

[1]BATTINI J M, NGUYEN Q H, HJIAJ M. Non-linear finite element analysis of composite beams with interlayer slips[J]. Computers and Structures, 2009, 87(13/14): 904-912.

[2]DALL′ASTA A, ZONA A. Non-linear analysis of composite beams by a displacement approach[J]. Computers and Structures, 2002, 80(27-30): 2217-2228.

[3]DALL′ASTA A, ZONA A. Slip locking in finite elements for composite beams with deformable shear connection[J]. Finite Elements in Analysis and Design, 2004, 40(13/14): 1907-1930.

[4]DALL′ASTA A, ZONA A. Three-field mixed formulation for the non-linear analysis of composite beams with deformable shear connection[J]. Finite Elements in Analysis and Design, 2004, 40(4): 425-448.

[5]GIRHAMMAR U A, PAN D H. Exact static analysis of partially composite beams and beam-columns[J]. International Journal of Mechanical Sciences, 2007, 49(2): 239-255.

[6]SOUSA JR J B M, OLIVEIRA C E M, DA SILVA A R. Displacement-based nonlinear finite element analysis of composite beam-columns with partial interaction[J]. Journal of Constructional Steel Research, 2010, 66(6): 772-779.

[7]RANZI G, DALL′ASTA A, RAGNI L, et al. A geometric nonlinear model for composite beams with partial interaction[J]. Engineering Structures, 2010, 32(5): 1384-1396.

[8]FRAGIACOMO M, AMADIO C, MACORINI L. Finite-element model for collapse and long-term analysis of steel-concrete composite beams[J]. Journal of Structural Engineering, 2004, 130(3): 489-497.

[9]KIM B, WRIGHT H D, CAIRNS R. The behaviour of through-deck welded shear connectors: an experimental and numerical study[J]. Journal of Constructional Steel Research, 2001, 57(12): 1359-1380.

[10]ZONA A, RAGNI L, DALL′ASTA A. Finite element formulation for geometric and material nonlinear analysis of beams prestressed with external slipping tendons[J]. Finite Elements in Analysis and Design, 2008, 44(15): 910-919.

[11]李偉. 大跨度斜拉橋靜動力可靠度分析[D]. 廣州: 華南理工大學, 2010: 53-55.LI Wei. Structural static and seismic reliability analysis of long-span cable-stayed bridges[D]. Guangzhou: South China University of Technology, 2010: 53-55.

Stochastic finite element reliability analysis of

composite beams considering longitudinal slip

JIA Buyu, YU Xiaolin, YAN Quansheng

(School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China)

Abstract：Steel-concrete composite beams are characterized by complex structure, material variety, and strong uncertainty, thus it is necessary to analyze them from the view of randomness. Based on the Newmark geometric model, considering the concrete slab, steel beams, and shear connectors as a whole element,and making use of the T.L. column incremental method, a nonlinear composite beam element model was developed by taking the longitudinal slip effect into consideration. Then, based on the model, and the characteristics of composite beams, structural response gradients of composite beams were obtained by the direct differentiation method (DDM), while the reliability index was achieved using the FORM method. For proof of reliability, an example steel-concrete composite beam was analyzed by the stochastic finite element program. The results show that, for practical engineering, it does not need a completely rigid connection to ensure structural reliability. However for security, it is necessary to consider geometric nonlinearity in the calculation of structure reliability.

Keywords：steel-concrete composite beam; longitudinal slip; nonlinear composite beam element; direct differentiation method; stochastic finite element; reliability analysis; geometric nonlinearity

通信作者：余曉琳,E-mail:xlyul@scut.edu.cn.

作者簡介：賈布裕(1983-), 男, 博士后;

基金項目：國家自然科學基金資助項目(51208208)；中國博士后科學基金資助項目(2013M542174)；中央高校基本科研業務費專項資金資助項目(2014ZZ0019,,2015ZM114).

收稿日期：2014-04-07.

中圖分類號：U448.27

文獻標志碼：A

文章編號：1006-7043(2015)12-1554-06

doi:10.11990/jheu.201404024