光刻機工件臺宏微電機的非線性復合控制

孫永倩 ，陳德運，劉川

(1.哈爾濱理工大學 計算機科學與技術學院，黑龍江 哈爾濱 150080; 2.哈爾濱工業大學 航天學院, 黑龍江 哈爾濱 150001)

光刻機工件臺宏微電機的非線性復合控制

孫永倩1，陳德運1，劉川2

(1.哈爾濱理工大學 計算機科學與技術學院，黑龍江 哈爾濱 150080; 2.哈爾濱工業大學 航天學院, 黑龍江 哈爾濱 150001)

摘要：針對光刻機工件臺長行程直線電機宏動和平面電機高精密微動的耦合運動特點，提出一種宏動跟蹤微動的變增益非線性復合控制方法，實現系統高動態納米級精度的跟蹤定位。宏動長行程直線電機采用零相位跟蹤前饋控制和雙環控制，實現系統無靜差跟蹤加速度指令；利用擴張狀態觀測器觀測宏動系統的動態變化，補償系統中的耦合推力和其他擾動；微動平面電機采用變增益非線性控制，根據系統誤差幅值的大小，動態的改變控制器增益，以大增益抑制系統加減速時的低頻大幅值誤差，以小增益避免系統勻速運動時高頻噪聲的引入。實現系統穩定時間小于30 ms，跟蹤誤差小于20 nm的跟蹤，實驗結果表明：該方法可改善系統的動態性能和抗干擾能力，減小系統穩定時間，提高系統的跟蹤精度。

關鍵詞：光刻機；直線電機；平面電機；推力耦合；非線性復合控制

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20151104.1708.014.html

陳德運(1962-)，男，教授，博士生導師.

光刻機工件臺是高動態超精密伺服運動平臺，是光刻機的最重要部件之一。它要求在高速運動的情況下，采用長行程直線電機宏動和平面電機高精密微動的驅動方式，在較大行程內實現平臺高動態納米級的跟蹤定位。以ASML已經商用的最先進光刻機TWINSCAN NXT:1970Ci機型為例，掃描時工件臺最高速度大于0.5 m/s，加速度大于30 m/s2，套刻精度小于2 nm，穩定時間小于10 ms[1]。因此，選擇一種提高系統動態性能，減小系統穩定時間，準確控制平臺運動的控制算法顯得尤為重要。

在光刻機的直線電機宏動伺服系統中，系統中的擾動會造成伺服性能的下降，如：微動臺耦合推力、齒槽效應、端部效應力、摩擦力、紋波推力等非線性因素[2-3]，而在平面電機微動伺服系統中，同樣也存在一些因素造成伺服性能的下降，如：宏動臺耦合推力、氣浮軸軸承氣隙不均勻引起的振動、線纜臺擾動、測量噪聲等因素[4-8],而且宏動直線電機和微動都存在電機名義模型與真實模型之間的建模誤差。X.S.Deng[9]研究了掩模臺的宏動直線電機，采用PID加干擾觀測器的方法提供宏動控制系統的干擾抑制能力。楊一博[10]著重分析了工件臺單自由度宏-微系統的耦合關系，結合執行電機的電磁特性給出了頻域的耦合模型并進行了分析，控制方法依然以PID為主。迭代學習控制(iterative learning control,ILC)方法可以有效處理掩模臺微動電機控制的前饋問題[11]，但對于掃描軌跡變化的工件臺，ILC方法每掃描一個硅片都需要重新進行學習，降低了工作效率。

本文針對光刻機工件臺宏動臺和微動臺的耦合運動特點，建立其單自由度動力學方程，提出一種宏動跟蹤微動的變增益非線性復合控制的方法，分別給出宏動直線電機和微動平面電機的控制策略，最后通過實驗驗證方法的有效性。

1宏微運動系統模型

在光刻機工件臺曝光掃描過程中，對y向要求最為苛刻，因此本文選擇工件臺的y向運動作為研究對象，首先建立光刻機工件臺宏微控制的等效模型，如圖1所示。宏動臺由直線電機驅動，氣浮導軌導向；微動臺由平面電機驅動，由固定在宏動臺上的氣浮軸承支撐；平衡質量塊也是由氣浮導軌導向，用于克服宏微電機運動相對基礎框架的沖擊。用光柵尺測量宏動臺相對基礎框架的位移yL，用激光干涉儀測量微動臺相對基礎框架的位移yS，用霍爾傳感器測量宏動臺和微動臺之間的相對位移yV，用光柵尺測量平衡質量塊相對基礎框架的位移yB，其中，yS≥yL；宏動臺的質量為M，微動臺的質量為m；宏動直線電機力輸入為FL，微動音圈電機力輸入為FS，宏動臺與平衡質量塊之間的阻尼與剛度分別為cL、kL，微動臺與宏動臺之間的阻尼與剛度分別為cS、kS，宏動和微動中的推力擾動分別為dM和dm。

圖1　宏微控制等效模型Fig.1　Equivalent of a macro-micro-control model

考慮最后的實驗驗證中，存在宏動和微動之間力的耦合作用。模型的動力學方程為

(1)

(2)

系統的狀態方程為

(3)

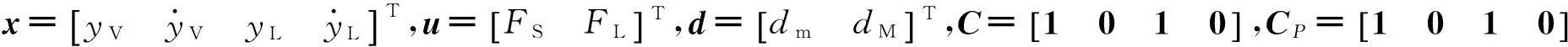
A=

因為整個系統是氣浮結構，宏動臺與平衡質量塊之間的阻尼與剛度cL、kL分別為零，微動臺與宏動臺之間的阻尼與剛度cS、kS也均為零。

2宏微電機控制器設計

2.1　控制器結構圖

在宏觀視覺上，光刻機宏動臺與微動臺的運動方式為宏動臺“背著”微動臺運動，宏動直線電機驅動宏動臺進行高速大行程微米級精度運動，微動平面電機驅動微動臺進行低速小行程納米級精度運動。針對光刻機工件臺高動態超精密納米級定位的宏微運動特點，提出以微動臺為主，宏動臺為輔，宏動臺跟蹤微動的控制策略，以宏動臺與微動臺之間的相對運動位移之差作為宏動臺的控制輸入，在拓寬微動臺運動行程的同時，實現納米級精度的跟蹤定位，控制器具體設計如圖2所示。

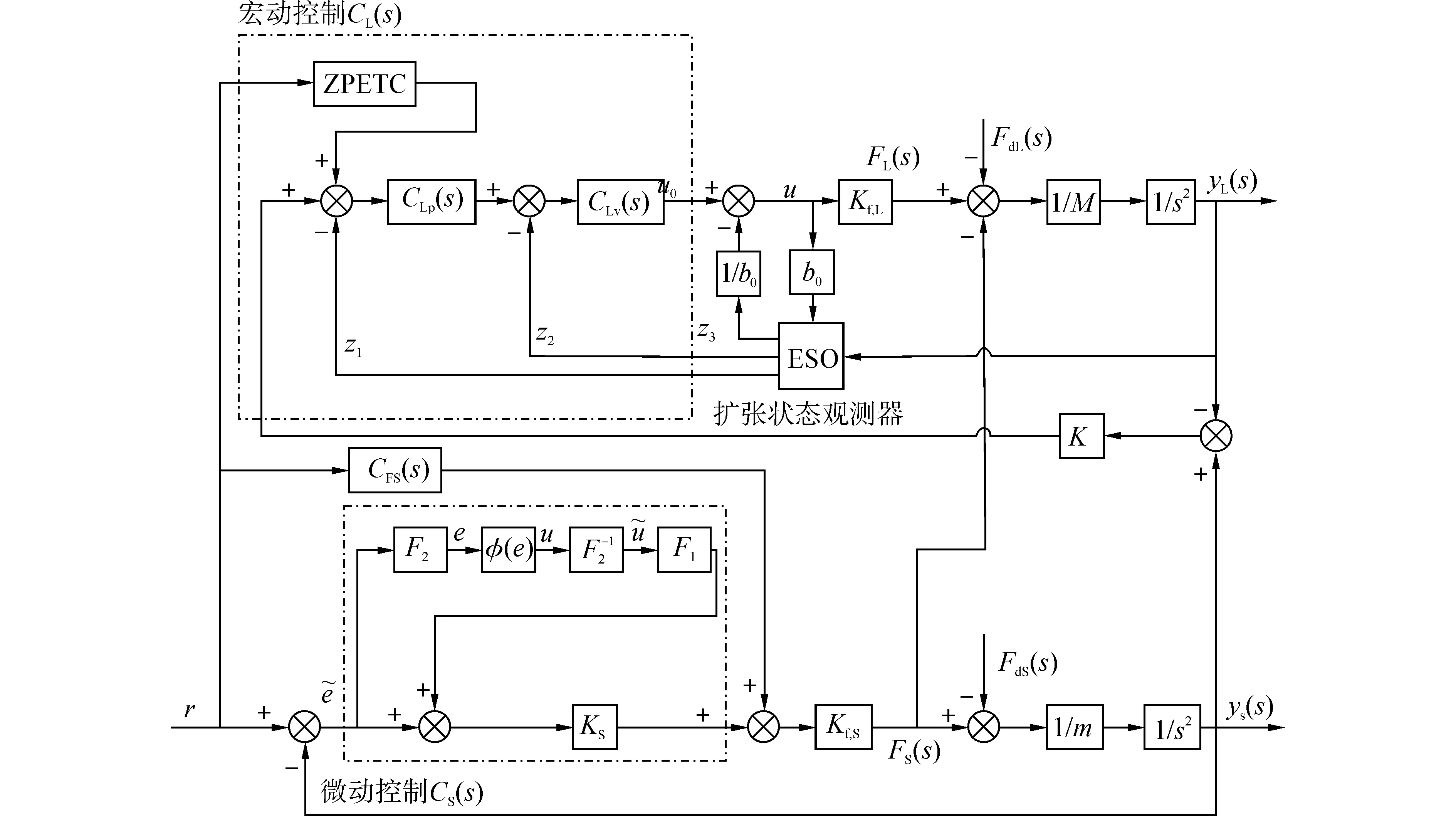
圖2　工件臺雙回路主從式宏微控制器結構Fig.2　Double loop master-slave macro-micro-motion controller structure of wafer stage

宏動直線電機控制器包括控制器CL(s)和狀態觀測器ESO[12]，設計控制帶寬為40Hz；微動平面電機控制器包括反饋控制器CS(s)和前饋控制器CF(s)，設計控制帶寬為200Hz。系統的控制跟蹤精度主要使用移動平均差(MA)和移動標準差(MSD)[13]來衡量，MA和MSD定義為

(4)

(5)

式中：Tsc為曝光時間，數值上等于狹縫長度除以掃描速度；ti為曝光點i處于狹縫中間對應的時刻，以所有曝光點的最大值作為MA和MSD的衡量指標。

2.2　宏動電機控制器設計

宏動電機控制器CL(s)采用雙環PID控制器，在保證系統穩定性及抗干擾能力的同時，通過配置系統零極點，提高系統的動態響應能力。速度環控制器CLv(s)采用比例和積分控制，以提高系統剛度、抑制干擾、減小電機力矩波動等不利因素帶來的影響。位置環控制器CLp(s)采用比例和微分控制，確定宏動系統帶寬，保證宏動臺位置的動態跟蹤精度和定位精度。速度環和位置環控制器可以表示為

(6)

在文獻[12]中，詳細論述了如何采用ZPETC提高系統動態性能和如何采用ESO觀測系統狀態以及補償系統擾動，本文就不再詳述。

2.3　微動電機控制器設計

微動電機控制器由前饋控制器與反饋控制器組成，前饋控制器主要作用是根據軌跡變化，實時增減電機推力，減小加減速時的誤差；反饋控制器則主要用以提高系統魯棒性并確保勻速運動時跟蹤精度。

2.3.1微動臺平面電機結構分析

微動臺要在空間內實現X、Y、Z、Rx、Ry、RZ6個自由度方向的跟蹤與定位，因此其電機設計為6個：3個洛倫茲電機F1、F2和F3組成的平面電機負責水平方向的運動與旋轉，運動行程為±2mm；3個洛倫茲電機Fz1、Fz2和Fz3負責垂直方向的運動與旋轉，電機布局如圖3(a)所示。微動臺電機為六自由度模型，將其分解為6個單自由度模型，以實現對電機的控制，圖3(b)為水平方向微動臺本體和平面電機動子的單自由度結構模型，圖3(c)為微動臺本體和平面電機動子單自由度力學模型。c12為電機動子與微動臺本體之間的阻尼系數，k12為電機動子與微動臺本體之間的剛度系數，m1為平面電機動子的質量，m2為微動臺本體的質量，微動臺的總質量為m=m1+m2，由此可得模型的動力學方程為

圖3　電機布局與力學分析Fig.3　Electrical and mechanical layout analysis

(7)

式中：q4=m1m2，q3=(m1+m2)c12，q2=(m1+m2)k12，c12=9Ns·m-1，k12=1.3×108N·m-1，m1=4.95kg，m2=17.55kg，m=m1+m2=22.5kg。

2.3.2微動電機前饋控制器設計

光刻機工件臺的軌跡規劃為4階S曲線，包括：位移x、速度v、加速度a、加加速度j和加加速度的斜率d，前者為后者的積分，以使規劃的軌跡平滑。如果期望系統無靜差的跟蹤4階S曲線r，則要求前饋控制器CF(s)滿足：

(8)

又因為c12=9 (N·s)·m-1，相比m1、m2和k12的值，c12的值偏小，為方便前饋的實現，將其省略，則有

(9)

2.3.3微動電機反饋控制器設計

在硅片的曝光掃描過程中，臺體沿y方向掃描，軌跡規劃為4階S曲線，而速度分為4段：加速段，調整時間段、勻速段和減速段。質量m=22.5kg的微動臺，在以amax=15m/s2進行加、減速時，位置誤差的特點為低頻大幅值；而在勻速掃描段，位置誤差的特點為高頻小幅值，誤差包括系統穩態誤差和高頻噪聲。針對微動臺的這一運動誤差特點，提出微動控制器采用N-PID反饋控制器[14]的控制方法，在以高動態加、減速時，微動控制器設計為高增益，快速抑制低頻大幅值誤差，減少系統穩定時間；在勻速掃描時，控制器設計為低增益，對高頻小幅值誤差進行抑制的同時，也不會放大噪聲；再采用二階低通濾波器抑制系統控制信號中的高頻噪聲，對于2.3.1節中未建模動態的諧振，用陷波器將系統控制信號中的諧振頻率有效衰減。

微動臺控制器Cs(s)包括：非線性函數φ(e)和控制器Ks、濾波器F1(s)和濾波器F2(s)，結構如圖2所示。非線性函數φ(e)定義為

(10)

式中：非線性增益系數a>0，閾值因子δ≥0，φ-(δ)=φ+(δ)，系統的控制量隨時間變化為連續。

控制器Ks定義為

(11)

(12)

(13)

其中，PID控制器Cpid(s)定義為

(14)

二階低通濾波器Flp,i(s)定義為

(15)

陷波器Fn,i(s)定義為

(16)

3實驗分析

實驗臺為自主研制的光刻機工件臺，宏動采用直線電機氣浮及其驅動裝置，位置測量采用光柵尺；微動采用平面電機氣浮及其驅動裝置，位置測量采用激光干涉儀。其中，上位機負責控制指令的發送，包括運動軌跡的規劃；下位機采用德國ELMA21槽VME64X機箱，內嵌VxWorks操作系統及其板級驅動包BSP，版本為6.4；運動控制卡為自制版卡，采用TI公司的TMS320C6416型DSP芯片，主頻1GHz，負責微動平面電機的解耦和宏微電機的實時控制；宏動臺質量M=148kg，微動臺質量m=22.5kg。實驗時，工件臺的運動軌跡采用4階S曲線，曲線參數分別為：y=0.056m,vmax=0.25m/s, amax=15m/s2, jmax=5×103m/s3,dmax=1×106。

在實驗中，狹縫長度為10mm，掃描速度為0.25m/s，加速時間為0.024s，加速時間之后為系統穩定時間、勻速掃描時間和減速時間。

圖4所示為宏動臺跟蹤微動臺的相對位移誤差曲線，此時微動臺為小增益控制(a=0,δ=0)。可見：在加減速時，最大誤差為300μm；在勻速運行時，誤差逐步減小；在0.05s時系統誤差趨于穩定，但誤差始終保持在一定范圍內，最大誤差為6μm。可以看出，在高動態的情況下，系統的跟蹤誤差受到低頻的干擾力作用而呈現出周期性波動。

圖4　宏微相對位移誤差Fig.4　Macro and micro relative displacement error

圖5~7分別為在小增益控制(a=0,δ=0)、非線性控制(a=3,δ=20)和大增益控制下(a=3,δ=0)微動臺跟蹤4階S曲線的誤差曲線。從圖5中可以看出，小增益控制因為系統增益偏小，動態性能不足，在加減速時，最大誤差為200nm，但這并不影響系統的收斂性，經過0.024s的加速段，再經過0.058s的調整時間后，達到系統誤差小于20nm的精度。

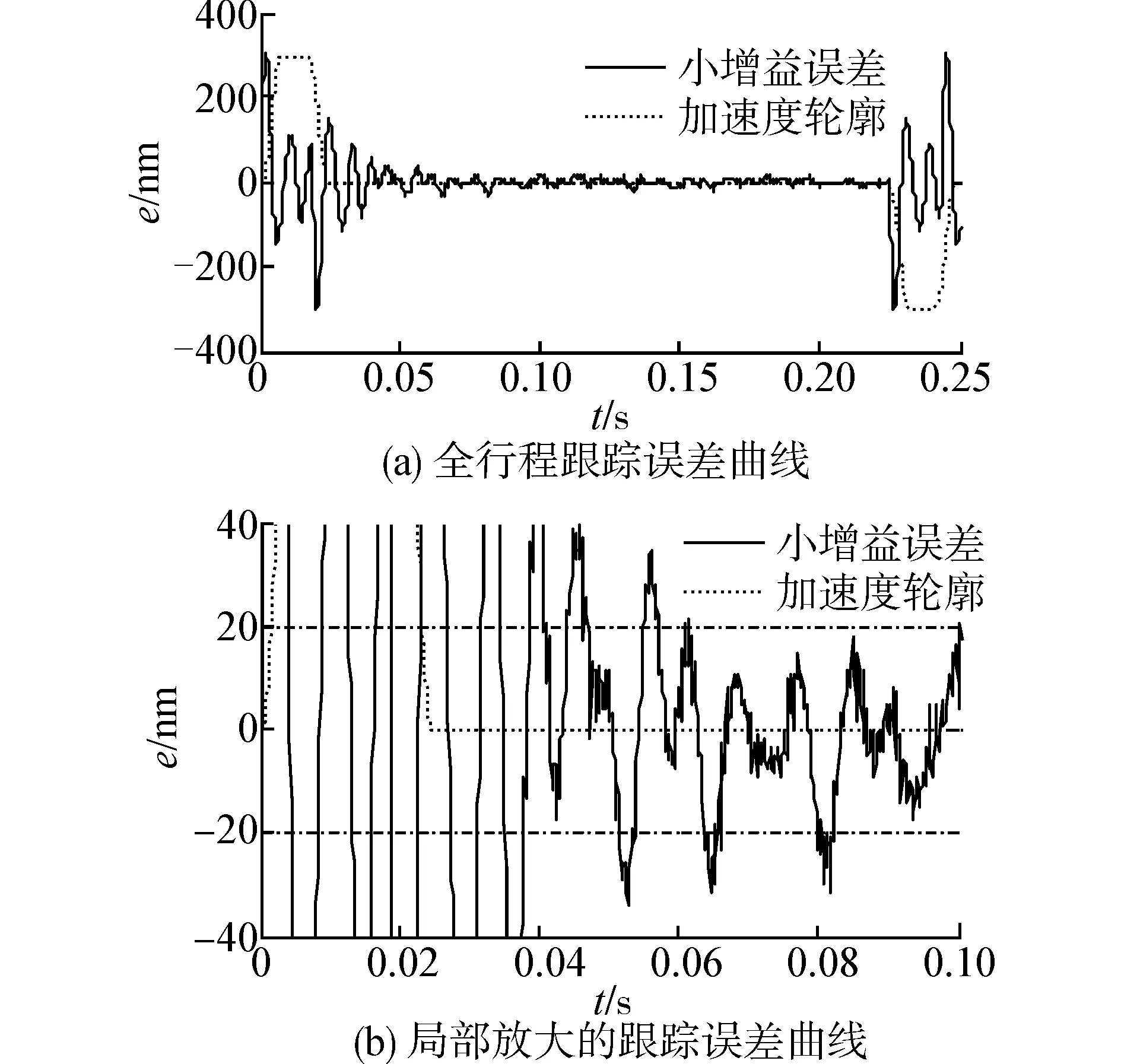
圖5　小增益控制下的跟蹤誤差Fig.5　Tracking error of small gain control

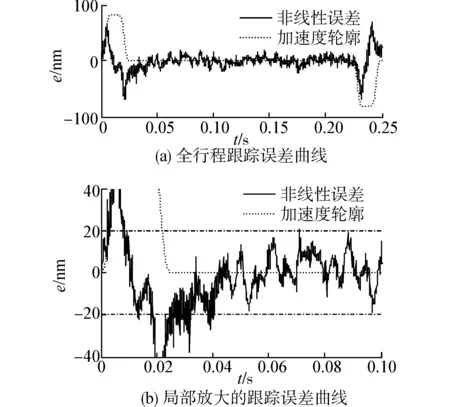
圖6　非線性控制下的跟蹤誤差Fig.6　Tracking error of nonlinear control

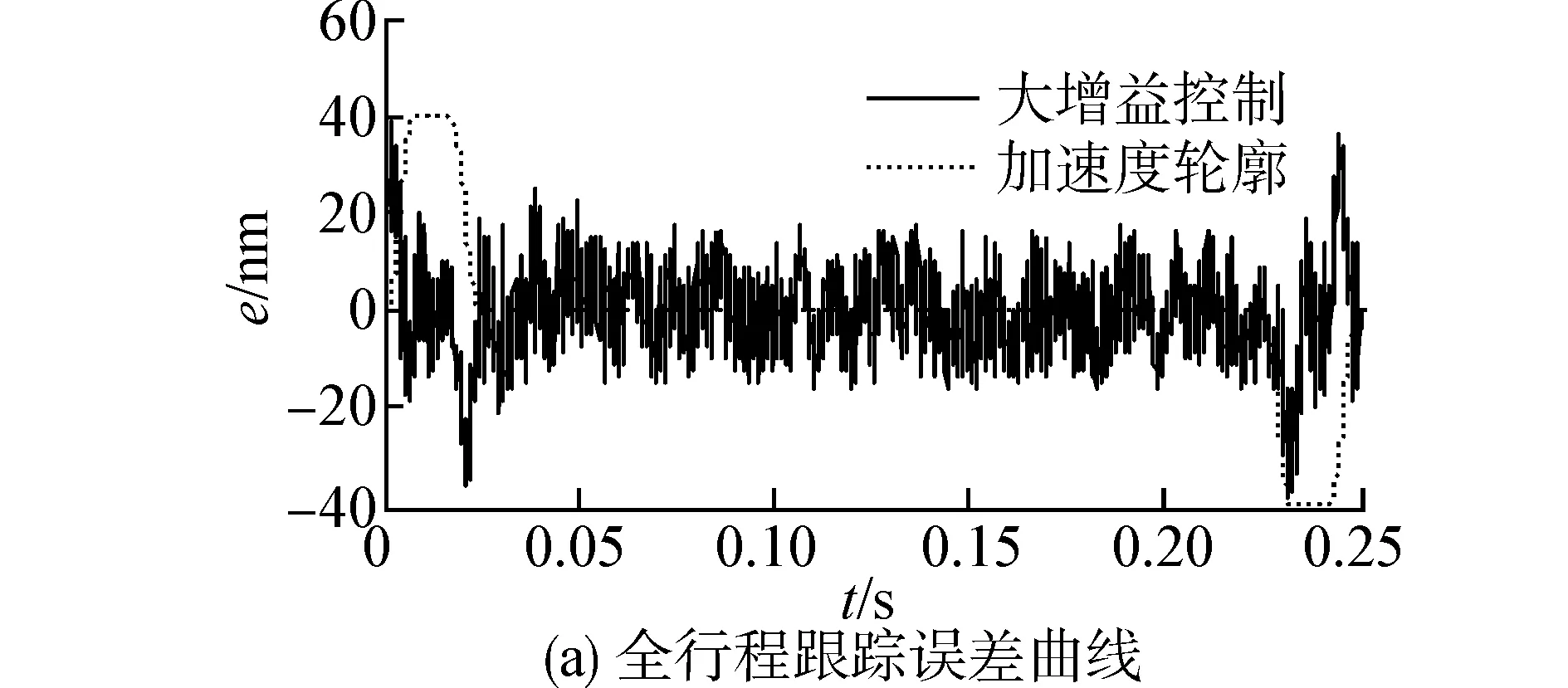
圖7　大增益控制下的跟蹤誤差Fig.7　Tracking error of large gain control

圖6為系統非線性控制下的誤差曲線，和小增益控制下的誤差曲線相比，系統動態性能得到增強，在加減速部分，系統最大誤差為80nm，經過0.024s的加速段，再經過0.018s的調整時間后，達到系統誤差小于20nm的精度。圖7為系統大增益控制下的誤差曲線，和前面2種控制方法的誤差曲線相比，系統動態性能更強，在加減速部分，系統最大誤差為50nm，經過0.024s的加速段，再經過0.014s的調整時間后，達到系統誤差小于20nm的精度。但是，將圖7和圖5、圖6對比可以看出，大增益控制下的跟蹤誤差曲線毛刺明顯增多，系統誤差中的高頻成分和前面2種方法相比，高頻成分明顯增多，這主要是因為系統增益加大，系統帶寬增大，激勵出機械諧振模態和引入了高頻噪聲。

圖8和圖9分別為3種控制方法的MA和MSD指標對比。從圖8中可以看出，小增益控制在經過0.046s的調整時間之后，達到MA指標小于3nm條件，主要原因是受系統動態性能的影響，所以調整時間較長；非線性控制和大增益控制在MA指標上，幾乎沒有差別，在經過0.026s的調整時間之后，都達到MA指標小于3nm的情況，2種算法在這個指標上相差無幾主要因為和MA指標統計的是低頻干擾有關。

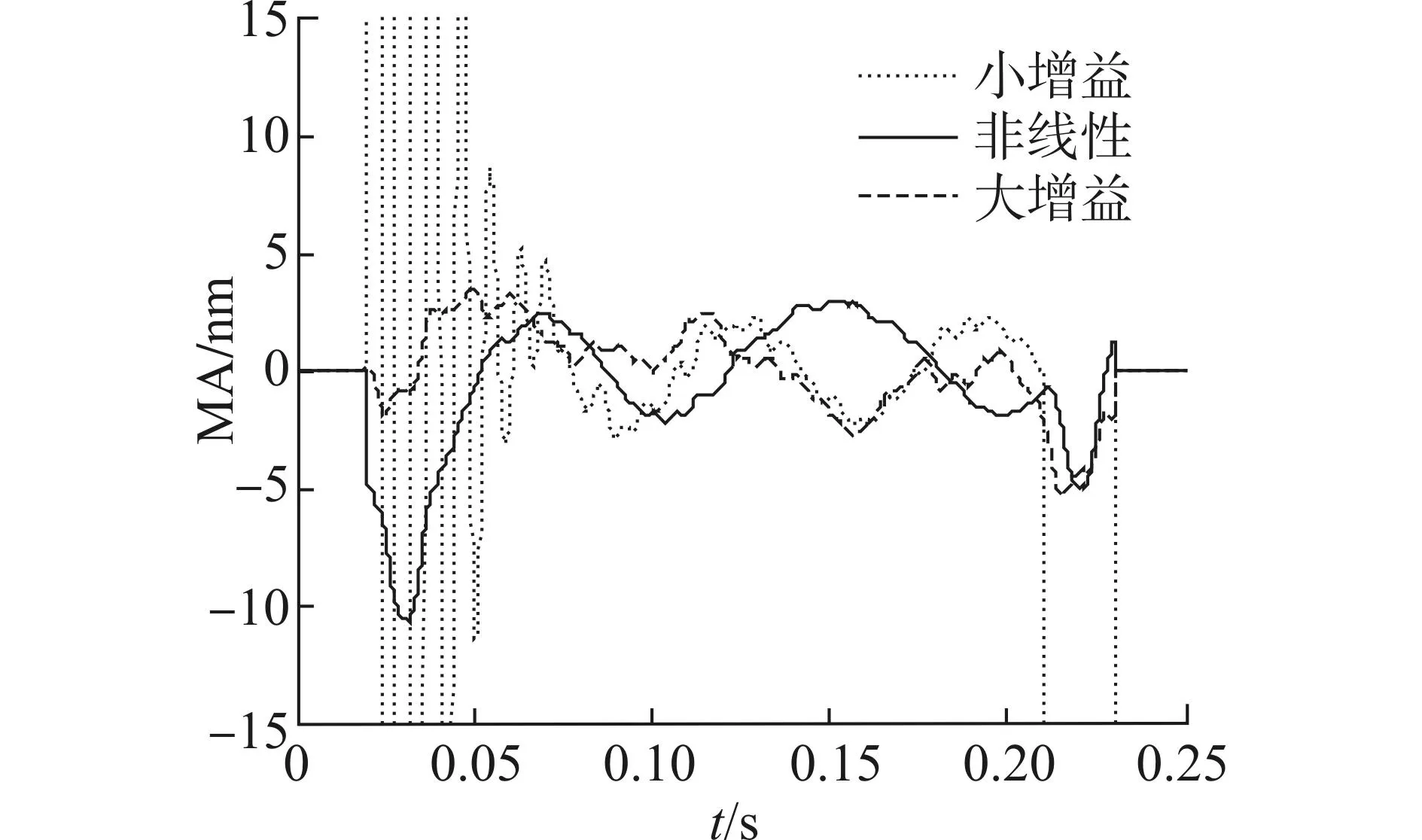
圖8　3種控制方法的MA指標Fig.8　The MA of the three control methods

圖9　3種控制方法的MSD指標Fig.9　The MSD of the three control methods

圖9為3種控制方法的MSD指標對比圖，可以看出，小增益控制和非線性控制的MSD指標隨著時間的推移，MSD指標逐漸減小，小增益控制下的MSD在第0.21s時取得最小值6nm；非線性控制下的MSD在第0.16s時取得最小值5nm；但是大增益控制由于受系統噪聲和模態的影響，MSD指標沒有隨時間的推移而逐漸減小，始終大于8nm，這對光刻機的曝光掃描是非常不利的。

表1為3種控制方法性能對比，表中所有時間，均為減去加速0.024s時間之后的調整時間。綜合各種指標，非線性控制和小增益控制相比，在指標相同的情況下，調整時間更短；非線性控制和大增益控制相比，在經過必須的調整時間后，各項指標更優。非線性控制相比其他2種方法，更適合應用于光刻機工件臺掃描曝光。

表1　3種控制方法性能對比Table 1　Performance comparison in the three controllers

在圖4中，宏動臺加、減速時，宏動臺與微動臺的相對位移誤差出現較大的誤差峰值，其原因在于：1)微動臺在加減速時，平面電機的作用力直接作用在宏動臺上，施加了一個與運動方向完全相反的作用力，從而使宏動臺誤差較大。2)宏動臺Y向電機驅動質量為148 kg，使電機動子產生較大的慣性時滯。

在圖5~7中，微動臺在加、減速時，系統誤差都出現較大的誤差峰值，且峰值的幅值隨著加速度的增大而增大，其原因在于：1)微動臺質量為22.5 kg，平面電機在加、減速時的系統沖擊較大，使得電機動子產生較大的慣性時滯；2)臺體的運動軌跡為4階S曲線，即系統有4階輸入指令，在前饋沒有完全實現的情況下，低階系統不能夠完全跟蹤4階輸入指令，系統將存在靜差，從而在加、減速時產生比勻速時更大的位置偏差；3)平面電機加減速時，控制指令的加減速變化較大，引起了繞組電流和磁阻推力的變化，從而造成較大的位置誤差。

在圖8中，MA指標隨著時間的推移而產生波動，其原因在于：1)宏動電機推力的波動引起微動臺的推力波動，在高速情況下，微動臺平面電機推力的反作用力直接作用在宏動臺上，盡管微動臺平面電機的帶寬比宏動電機的帶寬高，不像宏動臺波動那么明顯，這在指標上，也能得到反映。2)氣膜的干擾，宏動臺和微動臺都采用氣浮結構，氣膜的擾動引起臺體的波動。3)地基的振動，實驗臺暫時還未安裝在三級隔振臺之上，這也會引起臺體的振動。

4結論

1)宏動臺采用ZPETC和雙環PID控制，有效提高宏動系統跟蹤加速度信號的能力。

2)分析微動臺結構機理，建立微動臺本體和電機動子力學模型，引入4階前饋控制，提高微動系統動態性能。

3)運用非線性控制方法，根據微動臺誤差大小，動態改變微動系統增益，增強系統動態性能，減小系統穩定時間，提高系統跟蹤精度。

參考文獻：

[1]SCHMIDT R H M. Ultra-precision engineering in lithographic exposure equipment for the semiconductor industry[J]. Philosophical Transactions: Mathematical, Physical and Engineering Sciences, 2012, 370(1973): 3950-3972.

[2]BASCETTA L, ROCCO P, MAGNANI G. Force ripple compensation in linear motors based on closed-loop position-dependent identification[J]. IEEE/ASME Transactions on Mechatronics, 2010, 15(3): 349-359.

[3]楊俊友, 馬航, 關麗榮, 等. 永磁直線電機二維分段復合迭代學習控制[J]. 中國電機工程學報, 2010, 30(30): 74-80.YANG Junyou, MA Hang, GUAN Lirong, et al. Two-dimensional segmented synthesis iterative learning control of permanent magnet linear motor[J]. Proceedings of the CSEE, 2010, 30(30): 74-80.

[4]MIN Wei, ZHANG Ming, ZHU Yu, et al. Analysis and optimization of a new 2-D magnet array for planar motor[J]. IEEE Transactions on Magnetics, 2010, 46(5): 1167-1171.

[5]HU Tiejun, KIM W J. Extended range six-DOF high-precision positioner for wafer processing[J]. IEEE/ASME Transactions on Mechatronics, 2006, 11(6): 682-689.

[6]DE BOEIJ J, LOMONOVA E, VANDENPUT A. Modeling ironless permanent-magnet planar actuator structures[J]. IEEE Transactions on Magnetics, 2006, 42(8): 2009-2016.

[7]JANSEN J W, VAN LIEROP C M M, LOMONOVA E A, et al. Magnetically levitated planar actuator with moving magnets[J]. IEEE Transactions on Industry Applications, 2008, 44(4): 1108-1115.

[8]JANSEN J W, VAN LIEROP C M M, LOMONOVA E A, et al. Modeling of magnetically levitated planar actuators with moving magnets[J]. IEEE Transactions on Magnetics, 2007, 43(1): 15-18.

[9]DENG Xishu, WU Yunxin. Design of the macro-motion table control system for lithography stencil stage based on disturbance observer[C]//Proceedings of the 7th International Conference on Electronic Packaging Technology. Shanghai, China, 2006: 1-5.

[10]楊一博, 尹文生, 朱煜, 等. 粗精動超精密運動平臺系統建模與分析研究[J]. 中國機械工程, 2008, 19(23): 2773-2776.YANG Yibo, YIN Wensheng, ZHU Yu, et al. Modeling and analyzing for ultra-precision coarse-fine stage[J]. China Mechanical Engineering, 2008, 19(23): 2773-2776.

[11]OUYANG P R, ZHANG W J, GUPTA M M. An adaptive switching learning control method for trajectory tracking of robot manipulators[J]. Mechatronics, 2006, 16(1): 51-61.

[12]陳興林, 劉川, 周乃新, 等. 基于ZPET-FF和ESO的直線伺服魯棒跟蹤控制[J]. 上海交通大學學報, 2014, 48(5): 679-684.CHEN Xinglin, LIU Chuan, ZHOU Naixing, et al. Linear servo robust tracking control based on ZPET-FF and extended state observer[J]. Journal of Shanghai Jiaotong University, 2014, 48(5): 679-684.

[13]BUTLER H. Position control in lithographic equipment[J]. IEEE Control Systems Magazine, 2011, 31(5): 28-47.

[14]SU Y X, SUN Dong, DUAN B Y. Design of an enhanced nonlinear PID controller[J]. Mechatronics, 2005, 15(8): 1005-1024.

Nonlinear complex controller for macro and

micro movement of motors in the wafer stage

SUN Yongqian1, CHEN Deyun1, LIU Chuan2

(1. School of Computer Science and Technology, Harbin University of Science and Technology, Harbin 150001, China; 2. School of

Astronautics, Harbin Institute of Technology, Harbin 150001, China)

Abstract：For high-speed positioning with nm-level precision is required by using macro movement of long stroke linear motor and high-precision micro movement of planar motor in the wafer stage of lithography, a variable-gain nonlinear complex controller is proposed, in which the macro-motion tracks the micro-motion. The macro movement long stroke linear motor uses a double-loop direct velocity feed forward controller to eliminate static error when tracking acceleration. An extended state observer (ESO) observes the dynamic changes and compensates for coupling thrust and other disturbances in the macro system. The micro movement planar motor uses a variable-gain nonlinear controller, which changes the gain of the controller dynamically depending on the error magnitude. Using this method the gain of the controller is adjusted dynamically according to the magnitude of the system error. So that low frequency error is reduced by a large gain as the system accelerates or decelerates, and high frequency noise is rejected by a small gain as the system moves at constant speed. The experiment results show that system dynamic performance and disturbance resistance is improved, stabilizing time is reduced, and tracking precision is enhanced. The system settling time is less than 30ms with tracking error under 20nm.

Keywords：lithography; linear motor; planar motor; force coupling; nonlinear complex control

通信作者：孫永倩，E-mail:sunyongqian2003@163.com.

作者簡介：孫永倩(1979-)，女，副研究員；

收稿日期：2014-07-31.網絡出版日期：2015-11-04.

中圖分類號：V448.2

文獻標志碼：A

文章編號：1006-7043(2015)12-1620-06

doi:10.11990/jheu.201407075