城市公共交通網(wǎng)絡容量研究

劉 巖，邵 巖，王利杰，鄭明明，金曉瓊

(大連交通大學 交通運輸工程學院，遼寧 大連 116028)*

0 引言

隨著城市化進程的加速，人們出行日益增加，城市的交通擁堵問題越來越嚴重.公共交通是解決城市擁堵問題最為有效的途徑，而城市公共交通網(wǎng)絡容量是城市公共交通的一項重要研究［1-2］.這項研究中包含:如何定義城市公共交通網(wǎng)絡容量;如何確定影響因素以及計算容量的大小.本文就城市公共交通網(wǎng)絡容量的相關內(nèi)容進行深入的研究.

1 城市公共交通網(wǎng)絡容量定義及影響因素

1.1 城市公共交通網(wǎng)絡容量定義

公共交通網(wǎng)絡容量的定義源于“容量”一詞［3］，也就是在既有的公共交通路網(wǎng)的條件下，車輛數(shù)目確定，發(fā)車頻率不變的情況下，為乘客提供服務的能力.

可以把公共交通網(wǎng)絡容量分為理想狀態(tài)網(wǎng)絡容量和實際狀態(tài)網(wǎng)絡容量.

(1)理想狀態(tài)網(wǎng)絡容量

在道路、設施及交通狀態(tài)理想的狀態(tài)下，單位時間內(nèi)，公共交通能夠提供的最大服務能力，即車輛數(shù).

(2)實際狀態(tài)網(wǎng)絡容量

以理想狀態(tài)網(wǎng)絡容量為基礎，對其進行實際的路網(wǎng)拓撲、線路等修正，得出實際狀態(tài)下的網(wǎng)絡容量.

1.2 城市公共交通網(wǎng)絡容量影響因素

(1)公共交通的發(fā)車頻率

公共交通符合排隊系統(tǒng)的特點，公共交通車輛的行駛車速一定時，降低發(fā)車頻率將會增加每輛車的乘客數(shù)量，但是會相應增加乘客等待的時間，公共交通的服務水平變低;如果提高發(fā)車頻率就意味著需要更多的公共交通車輛，會提高公共交通運營的成本，需要在兩者間找到一個能兼顧兩者利益的平衡點.

(2)公共交通網(wǎng)絡性能

公共交通線路具有網(wǎng)絡拓撲結構，而設計的公共交通網(wǎng)絡應該保證居民最大出行時耗不能超過相關規(guī)定的標準［4］.而且也必須滿足公共交通線路路網(wǎng)密度指標，即在市中心規(guī)劃的公共交通線路的路網(wǎng)密度應達到3～4 km/km2;在城市郊區(qū)應達到 2 ～2.5 km/km2.

(3)公共交通的車輛保有量

在現(xiàn)有的公交網(wǎng)絡之中安排一定量的公共交通車輛為乘客提供空間位移的服務.從供需上來看，乘客的需求與所提供的車輛兩者之間有一個平衡狀態(tài)，可以根據(jù)《城市道路交通規(guī)劃設計規(guī)范》規(guī)定的多少人擁有一輛標準公交車，也可以根據(jù)《城市道路交通管理評價指標體系》規(guī)定的萬人公交車輛擁有量，來確定公共交通的車輛保有量.

(4)滿載率

公交車輛滿載率是指公共汽車運營車輛運載乘客的平均滿載程度，是衡量車輛利用程度的重要指標.

滿載率，來源于美國對城市公共交通問題的研究，由于美國公共交通在居民出行中所占比例不大，在通常情況下，美國公共交通使用乘載率(即實際乘載人數(shù)與公交車輛座位數(shù)的比值)作為評價指標;在中國，乘客數(shù)遠遠多于公交上的座位數(shù)，所以不能用乘載率來研究，只能用滿載率，即:額定座位數(shù)加上允許站立的乘客數(shù)［5-6］.

(5)公交行駛車道的類型

公交車輛行駛車道共分為三類:與社會車輛混合行駛，無任何優(yōu)先行使權;公交車可優(yōu)先行駛的車道，但是未采用隔離設施或限制;物理隔離的專業(yè)公交行駛車道.隨著公交車輛在時間和空間上占有的資源越來越多，公共交通的運行時間會越來越少，速度會越來越快，有助于提高公交的網(wǎng)絡容量［7-8］.

2 城市公共交通網(wǎng)絡容量模型

2.1 一維時空消耗法模型

一維模型是以有效運營長度與運營時間的乘積作為時空總資源［9-11］，在此約束下計算公共交通的路網(wǎng)容量，即:

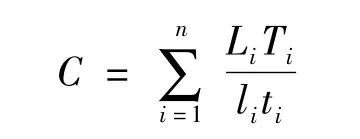
式中:l反為反應時間車輛行駛的距離，m;l制為車輛的制動距離，m;l安為車輛間的安全距離，根據(jù)國內(nèi)外實際使用的經(jīng)驗和理論分析，l安一般取用2 m;l車根據(jù)《城市道路設計規(guī)范(CJJ37-1990)》

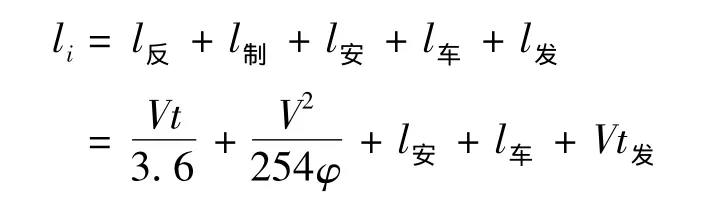
式中:C為城市公共交通路網(wǎng)容量;Li為第i輛公交車的運營線路長度，km;Ti為第i輛公交車每天的運營時間，h;ti為第i輛公交車按其規(guī)定線路運營一趟所需的時間，h;li為第i輛公交車兩車實際的車頭間距，km.安全車頭間距規(guī)定的設計車輛外廓尺寸取值，一般公交車的車身長度為12 m，即l車為12 m;l發(fā)為發(fā)車間隔時間內(nèi)車輛行駛的距離，m;V為行車速度，km/h;為駕駛員反應時間，t可取1 s;t發(fā)為車的發(fā)車間隔時間，h;φ與輪胎花紋、路面粗糙度、平整度、表面濕度、行車速度等因素有關.

這個模型中需要確定的參數(shù)有城市公交運營線路長度，運營總時間，和公交車按規(guī)定線路運行一趟的時間，公交車的發(fā)車間隔，行車速度及其對應的φ值.

2.2 時空消耗法的二維模型

二維模型是把有效運營面積乘以有效運營時間的作為時空總資源［9-11］，在此約束下計算公共交通路網(wǎng)容量，即:

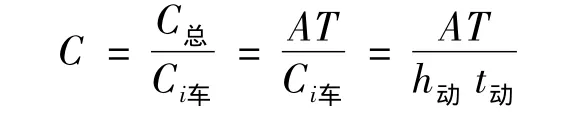
式中:C為公共交通路網(wǎng)容量，輛/單位時間;A為公共交通有效運營面積，m2;T為公共交通總有效運營時間，h;h動為公交車行駛過程中的平均車頭間距，km;t動為公交車在1 h內(nèi)平均出行時間，h.

該模型中有3個參數(shù)需要確定:公共交通有效運營面積A、公共交通有效運營時間和單輛公共車輛的平均時空消耗.公共交通有效運營面積是在城市道路面積的基礎上的一個修正值.

A=S交通× α公×R1×R2×R3×R4

式中:S交通為城市的道路面積，m2;α公為公交車道在城市道路中的比例;R1為道路等級修正系數(shù);R2為所處車道修正系數(shù);R3為路線使用頻率系數(shù);R4為其他干擾因素.

二維模型從面積入手考慮網(wǎng)絡容量，相對與一維模型更準確，更符合實際;加入多種修正系數(shù)更具有操作性和實用性.

2.3 基于排隊論的城市公共交通路網(wǎng)容量模型

排隊系統(tǒng)模型的參數(shù)共有六個，分別是X/Y/Z/A/B/C，X表示公交車輛到達公交停靠站的時間間隔分布;Y表示公交車輛在公交停靠站點停靠時間的分布;Z表示公交車站最多可提供的停車泊位數(shù);A表示公交車停靠站可停靠的總公交車輛數(shù);B表示在該公交車站需要再次公交車站停車的公交車輛數(shù);C表示服務規(guī)則(FCFS).

由于公交車輛一定會到達公交車站并且一定會離開公交車站，而且每輛公交車之間到達與否互不影響，并且考慮到計算等因素可以暫時將公交車輛到達公交車站的過程看作是泊松(Poisson)輸入過程.

由于公交車在公交車停靠站的服務時間與公交車上下乘客人數(shù)成正比，而公交車的乘客上下車是隨機事件，互不影響，所以公交車在公交車站的服務時間也可看作是一個負指數(shù)分布的服務模型.

因為一個公交站點可以提供的停車泊位數(shù)是有限的，文章中暫時將公交站點的平均停車泊位數(shù)定位5輛.考慮到計算等因素，文章中排隊系統(tǒng)的容量和顧客源數(shù)均視為∞.本文中的服務規(guī)則采用先到先服務原則(FCFS).

其中最關鍵的參數(shù)便是公交車輛的平均到達率λ和公交車停靠站的平均服務率μ.因為系統(tǒng)中所有數(shù)值的計算都離不開服務強度ρ，但是ρ=λ/μ.并且在泊松流和負指數(shù)分布之中λ和μ都是唯一的參數(shù).

首先需要測量所研究的公交站點所有線路公交車輛的到達頻率，則

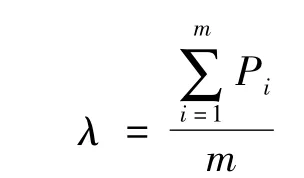
式中:λ為研究站點公交車輛的到達率，輛/h;Pi為研究站點第i路公交車的到達頻率，輛/h;m為研究站點的公交車線路數(shù)量.

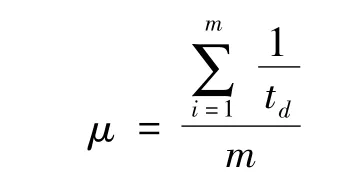
式中:μ為研究站點的服務率，輛/h;td為研究站點的公交車停留時間，h;m為研究站點的公交車線路總數(shù).

在排隊論系統(tǒng)之中一般ρ＜1時所研究的模型有意義.由于公交車站都會出現(xiàn)閑期(無公交車輛停靠)，所以1-ρ＞0，故ρ＜1.

則公交車停靠站系統(tǒng)可以看作是一個M/M/5/∞/∞/FCFS的排隊論系統(tǒng)模型.

所以此模型的平均排隊長度就是所研究的公交站點的平均達到公交車輛數(shù).則L=λ/(μ-λ)=ρ/(1- ρ).

按照前一節(jié)的結論可知某一個公交站點的平均公交車停靠數(shù)，并且所有公交車一定會走向某一個公交車停靠站，所以一個城市所有公交車停靠站的平均達到公交車輛數(shù)之和便是該城市的公共交通網(wǎng)絡容量.即

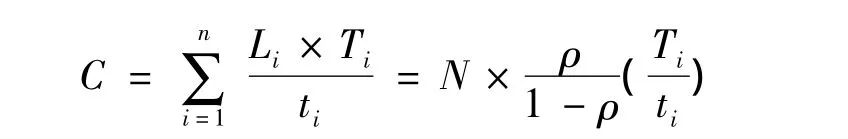
式中:C為城市公共交通網(wǎng)絡容量(輛);Li為第i個公交車站的平均達到公交車輛數(shù)(輛);N為公交車站的總數(shù);ρ為系統(tǒng)的服務強度(0＜ρ＜1);Ti為i路公交車的一天內(nèi)的總運營時間(h);ti為i路公交車的一次運營所需的時間，h.

對于一輛公交車，運營總時間與一次運營時間均相對固定，則可以擬合出公交路網(wǎng)容量與公交系統(tǒng)服務強度(0＜ρ＜1)的函數(shù)圖像如圖1所示.

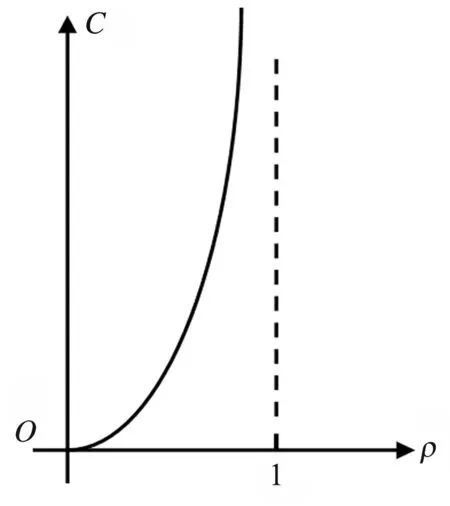
圖1 路網(wǎng)容量(C)與服務強度(ρ)函數(shù)關系圖

3 應用實例與分析

本文以大連市最具代表性的無軌電車101路、39路和有軌電車202路公交車為例，分別用時空消耗法與排隊論模型法計算公交車網(wǎng)絡容量.

3.1 一維時空消耗法模型計算路網(wǎng)容量

(1)101路公交車的運營時間是04∶25～23∶50，運營總時間T約為19.4 h.其線路運營總長度為 L=7.9 km，平均運營時間 t為0.67 h，101 路公交車的在高峰期間最小的發(fā)車間隔時間約為1.0min，行程速度為 11.85 km/h，則其對應的 φ 值為0.44.得出101路公交車的路網(wǎng)容量為1164輛.故由時空消耗法一維模型所得的C=1164輛.

(2)39路公交車的運營時間是06∶10～22∶40，運營總時間為16.5 h.其線路運營總長度為L=12.3 km，平均運營時間 t為1.0 h，39 路公交車的在高峰期間最小的發(fā)車間隔時間約為4.0 min，行程速度為12.3 km/h，則其對應的φ值為0.44.得出39路公交車的路網(wǎng)容量為248輛.

(3)202路公交車的運營時間是05∶30～22∶40，運營總時間T約為17.2 h.其線路運營總長度為 L=12.6 km，平均運營時間 t為1.0 h，202路公交車的在高峰期間最小的發(fā)車間隔時間約為4.0 min，行程速度為12.6 km/h，則其對應的 φ 值為0.44.得出202路公交車的路網(wǎng)容量為258輛.

3.2 二維時空消耗法模型計算路網(wǎng)容量

(1)由運營總長度為L=7.9 km，黃河路與長江路均為雙向六車道，假設每車道寬為3 m，則可知 S交通為165.9 ×103 m2，假設 α公為10%，等級修正系數(shù) R1為0.75，車道修正系數(shù) R2為0.95，車道平均使用頻率R3為0.80，路旁車輛干擾系數(shù)R4為0.85.則可知城市道路設施有效運營面積A為 8 573.7 m2，運營總時間 T=19.4 h，平均運營時間t為0.67 h.得出101路公交車的路網(wǎng)容量為1 184輛.

(2)根據(jù)以上步驟同理可以計算出39路公交車的路網(wǎng)容量為249輛(α公為15%、R1為0.80、R2為0.95、R3和R4為0.70).

(3)202路公交車的路網(wǎng)容量為260輛(α公為11.5%、R1為0.80、R2為0.95、R3為0.80、R4為0.85).

時空消耗法一維模型與二維模型所得的101路(1164和1184)、39路(248和249)和202路(258和260)公交車路網(wǎng)容量近似相等.

3.3 利用排隊論模型計算路網(wǎng)容量

由之前的排隊論模型可知計算平均排隊長度需要知道公交車的到達率λ與公交車停靠站的服務率μ.由101路公交車的發(fā)車間隔為1.5 min可知λ為40輛/h，由實際測量得到一輛101路公交車在車站平均停靠67 s，則μ為53.73輛/h.因此系統(tǒng)的服務強度ρ=λ/μ=0.744，則每個公交站101路平均排隊長度為2.91輛.則11個站點的總排隊數(shù)量為32輛.得出101路公交車路網(wǎng)容量C約為931輛.同理可知39路公交車的到達率λ=15輛/h，公交車停靠站的服務率μ=59輛/h，則服務強度ρ=0.254，可知39路公交車路網(wǎng)容量C約為113輛.同理可知202路公交車系統(tǒng)的服務強度為0.446 8，可求得202路公交車路網(wǎng)容量C約為264輛.

4 結論

從表1中可以看出時空消耗法一維與二維模型所計算的數(shù)值基本相等，但是利用排隊理論計算的數(shù)值出現(xiàn)一定的偏差.

排隊論模型計算公交車路網(wǎng)容量時由于模型敏感度很高，服務強度ρ有很小的波動也會引起路網(wǎng)容量值的較大變化.因此在利用排隊理論計算時一定要多記錄關于發(fā)車間隔與停靠時間的數(shù)據(jù)以便使數(shù)據(jù)誤差更小.

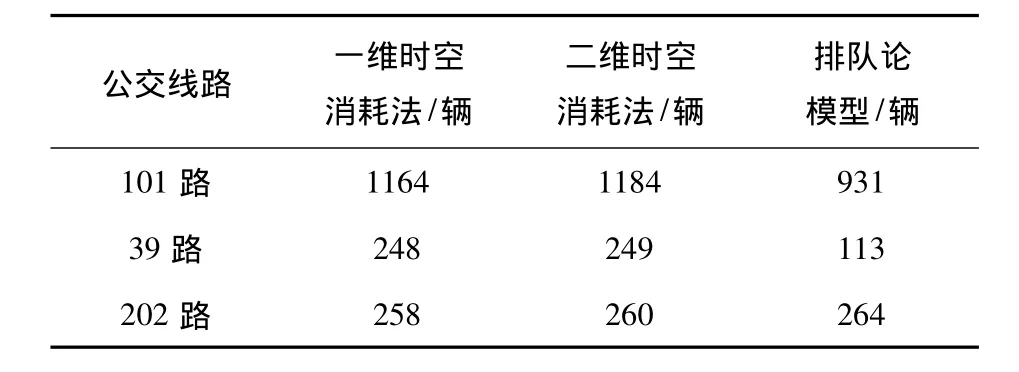
表1 不同模型的路網(wǎng)容量對比表

因此，在計算城市公共交通網(wǎng)絡容量時若對調(diào)查的數(shù)據(jù)精確度沒有保證時最好使用時空消耗法的一維模型與二維模型計算城市公共交通路網(wǎng)容量，但是計算過程較復雜.如果對于調(diào)查的數(shù)據(jù)比較有信心且系統(tǒng)的服務強度在0.43～0.48范圍內(nèi)時則可使用計算過程較簡便的排隊論模型計算城市公共交通路網(wǎng)容量.

［1］陳春妹，任福田，榮建.路網(wǎng)容量研究綜述［J］.公路交通科技，2002(3):97-101.

［2］徐吉謙.交通工程總論［M］.北京:人們交通出版社，2002.

［3］楊濤，陳建凱，於昊.城市中心區(qū)交通容量研究［J］.城市交通，2003(1):13-18.

［4］中華人民共和國交通部.JTJ01297 公路工程技術標準［S］.北京:人民交通出版社，1997.

［5］王貴明.綜合治理改善我國城市交通狀況的措施［J］.汽車工業(yè)研究，2010(2):36-41.

［6］王凌峰.改進公共交通設施和服務水平的建議［J］.交通標準化，2008(6):25-28.

［7］宋秀蓮，孫黎明，劉佳.大城市交通規(guī)劃研究［J］.天津市政工程，2009(4):34-36.

［8］曲大義，莊勁松，蔡國良，等.基于“服務水平”概念的路網(wǎng)總體容量計算模型［J］.青島理工大學學報，2008(5):23-27.

［9］YANG HAI，MOCHAEL G H.The capacity and level of service of urban transportation network［J］.Transportation Research Part，2000，B34:255-275.

［10］萬霞，陳峻，王煒.我國私人小汽車的使用和城市經(jīng)濟相關性研究［J］.城市規(guī)劃，2009(1):74-79.

［11］王煒，陳學武.城市交通系統(tǒng)可持續(xù)發(fā)展理論與體系研究［M］.北京:科學出版社，2004.