信息不對稱條件下拆遷糾紛動態議價模型的構建與分析

秦中伏，張明濤

（浙江大學 建筑工程學院，杭州310058）

一 引言

近年來，由城市房屋拆遷引發的利益沖突、矛盾激化，乃至惡性事件屢見不鮮，被國內媒體稱為“史上最牛釘子戶”的重慶楊家坪拆遷案、被稱為“最貴釘子戶”的深圳蔡珠祥案等，都說明了房屋拆遷糾紛的妥善調解是保障并推動拆遷工作的重要內容。

在這樣的背景下，對拆遷糾紛的研究已經成為近些年的熱點之一，研究的切入點也各有不同，其中以博弈分析為主要手段的研究較為廣泛。運用博弈論思想對拆遷糾紛進行定性分析方面，戶邑等從糾紛參與人的角度出發，以拆遷管理為切入點，分析了政府部門與拆遷人之間的博弈行為，指出政府既是拆遷的管理者、協調者，也是糾紛中有關爭議的仲裁者，并強調了政府在拆遷糾紛中角色的多重性［1］；Matthew S．Erie針對我國房屋拆遷糾紛中的“釘子戶”現象，分析了媒體的介入對拆遷問題的解決產生的影響［2］；彭小兵、李鐘書等借助博弈的基本思想，從糾紛當事人的角色定位、策略制定與調整、利益相互影響等方面提出了建議［3］［4］。在博弈論的分析方法的運用方面，鐘蔚借助囚徒困境模型，對拆遷中強征、抗征、行賄、上訪等行為對糾紛當事人的利益影響進行分析，從而為解決征地沖突提出了合理化建議［5］；朱念劬利用博弈矩陣和效用函數，對不同局勢下拆遷糾紛當事人的收益進行了比較，并基于多階段博弈模型提高了其研究成果與現實案例的吻合度，為當事人如何制定報價提供了指導［6］。從上述研究可知，利用博弈論基本思想對拆遷糾紛問題的研究需要建立符合現實狀況的博弈模型。

在拆遷糾紛中，當事人在拆遷補償額度上的爭奪往往成為糾紛的焦點，這一補償額度的爭議過程可被視作討價還價的過程。在這個過程中，當事者的還價受其保留價、時間壓力、對手類型、對手讓步模式與讓步多少、預期的對手將來的出價等諸多因素影響，同時，還會受局中人可能產生的互惠心理、公平心理、自我滿足感等主觀情緒的影響［7］。為此，一些學者運用討價還價理論探討拆遷糾紛產生的原因、影響要素以及解決方法。討價還價博弈的概念最早由納什（John Nash）提出，通過分析效用測度的無關性、帕累托有效、無關選擇的獨立性和對稱性，進而推導出納什討價還價解［8］。隨后，馬克·魯賓斯坦（Mar k Rubinstein）建立了完全信息輪流出價條件下的魯賓斯坦討價還價模型［9］。結合工程建設糾紛的特點，Toshihiko Omoto等利用討價還價模型對當事人如何在達成協議和申請仲裁之間做出選擇給出了建議［10］。考慮到當事人的議價能力對議價結果也會產生的重要影響，鄭鴻運用討價還價模型和糾紛當事人的收益比較，闡述了議價能力對討價還價的影響［11］46－50。考慮到拆遷糾紛問題中當事者之間往往是信息不對稱性的，向鋼華等對不完全信息相互威懾的討價還價模型進行了設計和研究，分析了不完全信息條件下相互威懾討價還價中的威懾可信性或沖突可能性［12］。從上述研究可以看出，基于議價過程的分析往往受到諸多主觀因素影響，與此同時，傳統分析的方式往往忽略了現實糾紛問題的主要特點，即信息的動態性和不對稱性，所以需要構建更加符合現實要求的議價分析模型。

本研究旨在基于拆遷糾紛問題復雜多變的實際特征，在魯賓斯坦討價還價模型中將信息不對稱性與動態性納入分析中來，通過構建信息不對稱條件下拆遷糾紛動態議價模型，對拆遷糾紛當事人給出補償議價的過程做出解釋，并對未來拆遷工作中拆遷補償的合理制定以及對有可能發生的議價糾紛進行預測，這對實現拆遷工作中糾紛的規避和將糾紛造成的損失最小化具有現實意義。

二 魯賓斯坦討價還價模型在拆遷糾紛問題中應用的局限性

在拆遷糾紛案例中較為常見的是糾紛當事人（一般為被拆遷方）對拆遷補償不能接受，并通過討價還價行為使雙方達成一個新的并被雙方共同接受的補償值。拆遷糾紛中的議價行為也屬于討價還價行為的一種。討價還價的概念最早由John Nash于1950年提出。隨著研究的不斷深入，直至1982年，美國學者魯賓斯坦（Ariel Rubinstein）建立了完全信息條件下輪流出價的討價還價模型。這一模型在經濟學界得到了廣泛認可，同時也為本研究提供了分析思路，但這一模型在拆遷糾紛問題中的應用仍有一定局限性。

（一）魯賓斯坦討價還價模型簡介

魯賓斯坦基于“分蛋糕”問題對基本的、無限期的完全信息討價還價過程進行了模擬，給出了完全信息條件下的輪流出價討價還價模型，即魯賓斯坦討價還價模型。

在該模型中，參與人1與參與人2分割大小為π（π＞0）的蛋糕，由參與人1首先提出分配方案，在輪流出價的過程中，若參與人一方接受對方分配方案，則雙方達成協議。魯賓斯坦的分析思路是根據最后被接受的報價提出者的不同，為該參與人提出最“合理”的報價值，這一報價是根據兩人議價能力（即貼現因子δ）而得出的一次性最優報價值。

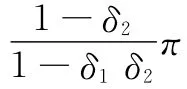
（二）魯賓斯坦討價還價模型在拆遷糾紛問題中應用的局限性

首先，在拆遷糾紛中的信息不是完全被局中人已知的。信息不對稱現象對現實問題的影響已經在市場投資［13］與交易糾紛［14］等眾多領域得到體現。而在拆遷糾紛問題中，信息不對稱性主要表現在兩個方面：一是局中人無法確定對方接受閾值是多少，所以“蛋糕”的大小理論上應該是未知的；二是局中人不能確定對方局中人的議價能力，任一局中人的真實議價能力都可能被故意掩飾［15］。

其次，拆遷糾紛議價過程中局中人的相關信息是動態變化的。從上述不同情況下的最優報價可知，當貼現因子與“蛋糕”大小已知的前提下，該最優報價是固定不變的，但是在現實的拆遷糾紛案例中，討價還價是一個反復進行的過程，局中人在每一輪討價還價過程中，自己的接受閾值和自信程度都可能發生改變，同時，局中人還會隨著議價的進程不斷更新對對方局中人相關信息的判斷。

因此，需要在借鑒既往研究成果的基礎上結合拆遷糾紛問題信息不對稱性和動態性的實際特點，對議價過程的要素進行重新設定，并構建出符合現實特征的議價模型。

三 信息不對稱條件下拆遷糾紛動態議價模型的構建

博弈論又稱對策論，其理論早于1944年便已提出，而對其研究也不斷深入，其中尤以美國數學家John Nash在20世紀50年代提出著名的“Nash均衡”這一概念為代表，不僅證明了非合作博弈及均衡解，也證明了均衡解的存在性。根據研究切入點的不同，逐漸有亞對策、軟對策、誤對策等理論的建立，而博弈類型也逐漸豐富，有合作博弈和非合作博弈、靜態博弈與動態博弈、完全信息博弈與不完全信息博弈等不同分類。討價還價行為屬于博弈的一種，但由前文可知魯賓斯坦討價還價模型僅適用于無限期的完全信息討價還價過程，所以需根據博弈分析的基本思想對上述模型進行完善。

（一）拆遷糾紛博弈的基本要素設定

從局中人的角度來看，雖然在現實的拆遷糾紛案例中常有政府、開發商、拆遷實施者和拆遷戶等多個主體共同參與，但是由于本研究重點關注的是拆遷糾紛中當事者之間的議價過程，所以本研究將拆遷糾紛博弈中的局中人分為拆遷方和被拆遷方。

從局中人策略的角度來看，在現實的拆遷糾紛案例中，雖然局中人常見的行為一般有議價（即討價還價，這其實是一個妥協或讓步的行為）、勸說、威脅（或恐嚇）、獎勵（或許諾）等，但是由于本研究的側重點在于拆遷糾紛中的議價過程。從拆遷糾紛的議價進程的角度來看，局中人的策略則可分為接受議價和不接受議價兩類。如果局中人的任何一方接受當前對方提出的議價，則議價終止，拆遷得以實現。如果局中人的任何一方不接受當前對方提出的議價，則要么提出新的議價，議價過程繼續進行，要么不再提出新的議價，等待對方接受自己的最后還價，如果對方接受自己的最后還價，則議價終止，拆遷得以實現，如果對方不接受自己的最后還價，則談判破裂，議價終止。

（二）信息不對稱條件下拆遷糾紛動態議價模型的要素設定

本研究對拆遷糾紛的議價環節做如下假定：局中人i（拆遷方）率先出價，此后雙方在信息不對稱條件下輪流出價，直到一方接受對方提議，或者談判最終破裂，議價過程結束。在議價開始時以及議價過程中，雙方都對自己的接受閾值（Plim）有所設定，且對對方的接受閾值有所預測；在議價過程中，雙方根據自己在當前情況下通過議價行為奪得利益的能力（自信度δ）和對對方的自信度的評判，交替報出在當前情況下對自己最為有利的議價（P）。綜上所述，可將信息不對稱條件下拆遷糾紛議價模型記述為：G＝｛N，Plim，δ，P｝。其中，N ＝｛i，j｝，Plim＝ ｛Pmaxii，Pminjj，Pmaxij，Pminji｝，δ＝ ｛δii，δjj，δij，δji｝，P ＝｛Pi，Pj｝。各要素的定義如下：

N＝｛i，j｝表示拆遷糾紛中的局中人，其中i表示拆遷方，j表示被拆遷方；

Plim表示局中人的接受閾值，其中Piimax和Pimjax分別表示i（拆遷方）可以給出的拆遷補償的最高價以及j（被拆遷方）對這一最高補償價的估計，Pjmjin和Pjmiin分別表示j（被拆遷方）所能接受的拆遷補償的最低價以及i（拆遷方）對這一最低補償價的估計；

δ表示局中人的自信度，其中δii和δij分別表示i（拆遷方）自己的自信度的大小以及j（被拆遷方）對i的自信度的估計，δjj和δji分別表示j（被拆遷方）自己的自信度的大小以及i（拆遷方）對j的自信度的估計；

P＝｛Pi，Pj｝表示拆遷糾紛中的局中人所給出的各自的議價值。

而在不同的議價階段（t），各方的接受閾值（包括對對方接受閾值的預測值）、各方自信度（包括對對方自信度的評判）以及在議價過程中的實際報價都會有所不同。因此，該模型還可以記述為：G（t）＝｛N，Plim（t），δ（t），P（t）｝，模型中各要素的具體形式與含義與上述表達類似。

（三）信息不對稱條件下拆遷糾紛動態議價模型的構建

根據魯賓斯坦討價還價模型在拆遷糾紛中的適用性分析可知，在推導拆遷糾紛議價值P（t）的過程中必須要考慮信息不對稱性和動態性。

首先要確定“蛋糕”的大小。在任何一輪議價時，局中人議價的起點都是自己上次的報價，而對于局中人來說能得到最多的利益就是對方局中人的接受閾值，但受信息不對稱性的影響，這一接受閾值的大小僅能靠局中人估測。因此，在第t次議價時，對i（拆遷方）而言，其上一次報價值是Pi（t－1），此時i根據j已經給出的Pj（t－1）推測出其新的接受閾值為Pjmiin（t－1），所以，對于i來說，“蛋糕”大小為Pjmiin（t－1）－Pi（t－1）。同理，對j（被拆遷方）而言，其上一次報價值是Pj（t－1），j根據i已經給出的Pi（t）推測出其新的接受閾值為（t），所以對于j來說，“蛋糕”大小為Pj（t－1）－Pimjax（t）。

其次，自信度δ是影響局中人議價報價的重要因素之一，引入自信度的概念用以表示糾紛當事人通過議價行為贏得目標報價的信心與能力，自信度隨時受到雙方議價情況的影響，也進一步影響雙方進一步議價值的確定。己方自信度越高，越不容易對“蛋糕”做出讓步；與此同時，對方自信度越高，越容易從己方爭得更多的“蛋糕”。與魯賓斯坦討價還價模型中貼現因子類似，自信度δ∈［0，1］，當δ＝0時，表示局中人完全失去了議價的能力，協議的最終報價將由對方主導；當δ＝1時，表示局中人有足夠的能力主導協議的議價值的最終確定。在信息不對稱條件下，影響局中人做出報價的是己方自信度和對對方局中人自信度的估計值。

綜上所述，可將信息不對稱條件下拆遷糾紛動態議價模型表達如下：

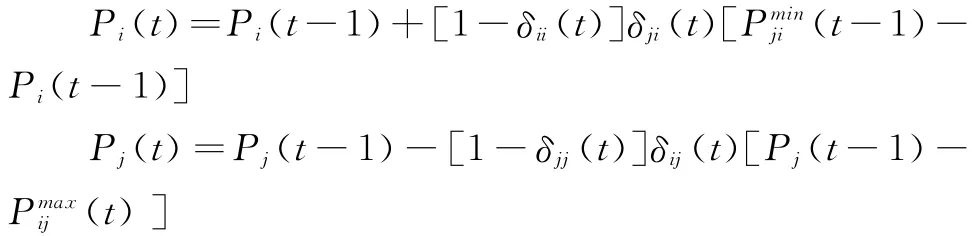
其中t≥1。

（四）自信度的影響因素與計算方法

在拆遷糾紛議價過程中，對對方當事人自信度的判斷，主要受到對方當事人報價、對對方當事人接受閾值的預測值的影響，同時也與對對方信息表述的真實性判斷有關。

首先，對方連續報價的變化幅度可以體現對方自信度的高低，兩次報價變化幅度越小說明其自信度越高，反之亦反。以拆遷方預測被拆遷房自信度為例，可表示如下式：

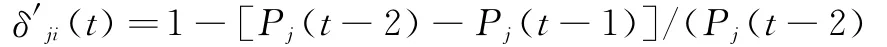
式中t≥2

其次，對方報價與對對方當事人接受閾值的預測值的差距也是己方當事人判斷對方自信度的主要依據，兩者差距越小，說明對方自信度較高，反之亦反，可表示如下式：

式中t≥1

上述兩式，前者是僅依據對方提供的信息進行判斷，后者則是己方當事人根據自己的預測進行判斷，定義真實性判斷系數τ（t），令0≤τ（t）≤1，其中τ（t）越趨近1，表示越相信，反之則表述不相信，則基于上述兩式可以得出對對方當事人的自信度預測值表達式如下：

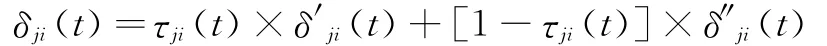
式中t≥2，而當t＝1時，被拆遷方還沒有連續報價，所以只能通過δ″ji（1）進行評價。

同理，被拆遷方對拆遷方的自信度預測的公式可以用如下公式表示：

上式中均有t≥1，當己方當事人對對方當事人自信度有了預測之后，則自身自信度會受到影響、發生變化。基于當事人的非理性特征，當雙方當事人自信度出現差異時，當事人會出現非理性情緒，如嫉妒、憤怒、攻擊等對抗情緒，或者如同情、謙讓、互利等合作情緒。分別用α和β表示當事人的對抗情緒敏感系數和合作情緒敏感系數，令α∈［0，1］且β∈［0，1］，當α（或β）越大，說明當事人容易被對方當事人的自信度所影響，相反地，當α（或β）越小，說明當事人越堅持自己的自信、不受對方影響。根據前文的分析，可將己方當事人自信度表達式表示如下：

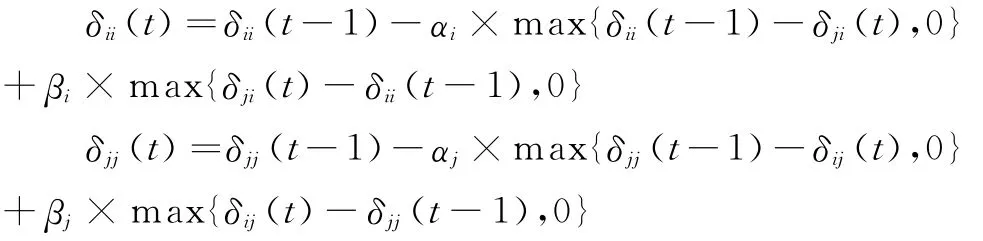
此處有t≥1。

四 基于信息不對稱條件下拆遷糾紛動態議價模型的案例分析

基于信息不對稱條件下拆遷糾紛動態議價模型，我們以被稱為“溫嶺最牛釘子戶”的羅保根拆遷案為例，通過模型構建與不同條件下的議價演算驗證該模型的適用性，并為如何在現實拆遷糾紛中規避、化解議價糾紛提供解釋。

（一）案例簡介與模型構建

溫嶺市火車站建設過程中，被征地農戶羅保根一家因不能接受拆遷補償方案而拒絕搬遷，其5層樓房屹立在新修建的馬路中間，經過該路段的車輛行人都得繞行而過，后經媒體報道后，被網民稱為“最牛釘子戶”。2008年，初次測量評估時，羅保根了解到自家粗略的評估價在28萬元左右，羅覺得“再商量下應該可以更高些，加個一兩萬總還是可以的，那就還可以接受”，但按照相關規定給出的最高補償額僅為26萬元，羅表示不能接受并拒絕該補償協議。2009年，溫嶺站落成，站前大道的建設于2011年春天動工，2012年夏季拆遷作業開始實施，由于羅家房屋在鄰居拆遷中受損，家中矮房也在家中無人時被拆遷方私自拆除，雙方關系日漸緊張。事件經報道后，政府相關部門開始介入，而此時羅家提出至少80萬拆遷補償才能同意拆遷，雙方僵持不下后，各級政府部門加強了與羅家的溝通協商，11月30日羅保根接受原補償標準，12月1日羅家原有住宅完成拆遷。

在此案例中，僅僅8天之內，羅保根一家的態度就從之前的“堅決不能接受”變成了“接受原拆遷補償方案”。針對該過程的猜想與分析，也成為了該事件結束后的話題熱點。為了更好地驗證該模型對拆遷糾紛議價的解釋作用，可根據已知信息將基于本案例的信息不對稱條件下拆遷糾紛動態議價模型構建如下：

局中人，即拆遷糾紛當事人N＝｛i，j│其中i為政府，j為被拆遷方羅保根｝；

策略，雙方策略均設定為接受協議并拆遷、不接受協議并繼續談判；

糾紛起點，即t＝0，設定為羅保根要求80萬元補償；

當任何一方的報價都超出了對方的接受閾值時，議價繼續進行，當有一方的報價被對方接受，則議價終止。

（二）基于不同條件設定下的演算分析與解釋

在上述案例的詢價階段中，t＝0，政府給出其在相關政策規定下所能給出的最高補償26萬元，而羅保根提出要求補償80萬元方可接受拆遷，但是其接受閾值是在28萬元的基礎上再多補一兩萬，設其為30萬元，故有如下表達：（單位：萬元）

此時由于有 Pi（0）＜ Pminjj（0），且 有 Pj（0）＞Pminii（0），所以雙方都不會接受對方報價，并進入議價階段。

為了驗證在不同自信度水平下雙方在議價過程中將給出不同程度的議價變化幅度，可對糾紛當事人雙方的自信度水平做（強，強）、（強，弱）、（弱，強）、（弱，弱）四種假設，根據議價模型公式可得出如下運算結果：

基于雙方自信度的情境假設（強，強） （強，弱） （弱，強） （弱，弱）i對j的接受閾值P min ji （1）的預測值70 40 70 40 i對j的自信度δji（1）的預測值0．875 0．5 0．875 0．5設定i的初始自信度δii（0） 0．95 0．95 0．7 0．7非理性情緒系數的設定 αi（1）＝0．2 αi（1）＝0．2 βi（1）＝0．2 αi（1）＝0．2 i的修正自信度δii（1） 0．935 0．86 0．735 0．66 i的議價值Pi（1） 28．5025 26．98 36．2025 28．38

從上表可知，當局中人j認為局中人有較高自信度時，會認為其接受閾值較為接近其報價，則設Pminji（1）＝70，否則設為Pminji（1）＝40；當局中人i自信度較高時，設其初始自信度為δii（0）＝0．95，否則設為δii（0）＝0．7；當局中人i認為其自身與局中人j自信度水平相當或者自身自信度高于對方自信度時，表現出對抗情緒，即此時僅有αi（1）存在，設αi＝0．2，而當局中人i認為自身自信度低于對方時，表現出合作情緒，即此時僅有βi（1）存在，并設βi（1）＝0．2。根據上述假設可運算得出i的議價值Pi（1），從結果中可得出，當局中人i認為其自身自信度高于對方自信度時，即（強，弱）組合，其報價讓步幅度是最小的；當局中人i認為雙方自信度水平相當時，報價讓步幅度水平相近；而當局中人i認為其自身自信度低于對方自信度時，即（弱，強）組合，其報價讓步幅度是最大的，這一結果基本符合實際糾紛案例。

同理可知，局中人j將在不同情境下給出自己的議價值，直到一方報價在自己的接受閾值范圍之內，議價過程結束。

而在本案例中，由于拆遷方有著相關制度政策的支持，其自信度極高，可視為δii＝1，所以在任何一次議價過程中都不會做出任何讓步，最終羅保根一家不得不將自身的接受閾值調整至26萬元，方達成一致，糾紛結束。這一案例雖具有一定特殊性，但也驗證了該模型的合理性。

五 結論

信息不對稱條件下拆遷糾紛動態議價模型針對現實拆遷糾紛問題中的普遍特點，在原有魯賓斯坦討價還價模型的基礎上做出了一定的完善，案例的演算與分析也驗證了該模型中相關因素對當事人議價的設定有直接影響。然而，該模型的構建不僅僅是用于解釋既有拆遷糾紛問題，而是試圖利用該模型預測在未來開展拆遷工作中可能會遇到的議價糾紛。在拆遷工作開展的過程中，制度政策、經濟利益以及當事人之間的信任程度等因素都直接影響議價模型中的各個因素。這也就意味著在開展拆遷工作的過程中，可以通過對上述因素的調整與修正來實現影響議價糾紛的目的，這也便是構建信息不對稱條件下拆遷糾紛動態議價模型的現實意義。而如何構建各個因素定制的指標體系，進一步強化定量計算的準確性，也是本研究有待進一步完善的方向。

［1］戶邑，劉貴文，彭小兵．城市拆遷管理的博弈分析［J］．重慶建筑大學學報，2005，（5）．

［2］ERIE M S．Property Rights，Legal Consciousness and t he New Media in China：The Har d Case of t he“Toughest Nailhouse in History”［J］．China Infor mation，2012，（1）．

［3］彭小兵，譚蓉，戶邑．城市拆遷糾紛的博弈分析及對策建議［J］．重慶大學學報（社會科學版），2005，（5）．

［4］李鐘書，翁里．論城市拆遷中社會利益和經濟利益的博弈［J］．安徽大學學報，2004，（4）．

［5］鐘蔚．城市化進程中征地利益博弈的沖突行為分析與公共治理思路［J］．現代經濟探討，2013，（4）．

［6］朱念劬．拆遷補償中的多階段博弈模型研究［J］．中國房地產，2013，（6）．

［7］紀淑娟，張純金，梁永全，劉寶華．一次性雙邊討價還價中參與者讓步動機的理性分析與驗證［J］．中國管理科學，2013，（S2）．

［8］NASH J F，Jr．The Bar gaining Proble m［J］．Econo metrica，1950，（2）．

［9］Ariel Rubinstein．Perfect Equilibriu m in a Bargaining Model［J］．Econo metrica，1982，（1）：97－109．

［10］OMOTOT，KOBAYASHI K，ONISHI M．Bargaining Model of Construction Dispute Resolution［C］／／Systems，Man and Cyber netics．IEEE Inter national Conference，2002．

［11］鄭鴻．征地補償安置討價還價博弈分析［D］．福州：福建農林大學，2012．

［12］向鋼華，王永縣．一種不完全信息相互威懾討價還價模型［J］．運籌與管理，2008，（6）．

［13］LA MBERT R A，LEUZ C，VERRECCHIA R E．Inf or mation Asy mmetr y，Infor mation Precision，and the Cost of Capital［J］．Review of Finance，2012，（1）．

［14］LAUERMANN S．Dynamic Matching and Bargaining Games：A general Approach［J］．American Econo mic Review，2013，（2）．

［15］周筱蓮，莊貴軍．討價還價的博弈模型及其現實補充［J］．西安財經學院學報，2011，（3）．