基于有限元方法高壓開關柜電場的優化設計

代佳佳，苗紅霞

(1. 河海大學 能源與電氣學院, 江蘇 南京 210098； 2. 河海大學 物聯網工程學院, 江蘇 常州 213022)

?

基于有限元方法高壓開關柜電場的優化設計

代佳佳1，苗紅霞2

(1. 河海大學 能源與電氣學院, 江蘇 南京 210098； 2. 河海大學 物聯網工程學院, 江蘇 常州 213022)

摘要：高壓開關柜的電場分布會影響其絕緣性能，研究和改善高壓開關柜中的電場分布是當今高電壓技術的重要任務之一。基于有限元軟件ANSOFT-MAXWELL對40.5 kv的高壓開關柜內部電場進行3D建模仿真，并分析其靜電場分布情況，采用MAXWELL自帶的參數化和目標優化設計功能，對高壓開關柜內的結構進行優化設計，得到了使高壓開關柜內部結構表面電場強度分布最均勻的結構值。

關鍵詞：高壓開關柜；電場強度；優化設計

0引言

隨著國家電網的快速發展和高壓開關柜的廣泛使用，高壓開關柜事故也屢見不鮮。事故主要表現在絕緣事故、載流故障、機械事故、誤動事故和拒動事故等[1-4]，其中絕緣事故尤為突出。由于氣體絕緣開關柜采用金屬封閉結構，斷路器、開關等元器件均密封在SF6氣室內，因為SF6氣體絕緣性能對電場均勻性的敏感性要遠大于空氣，所以，在開關柜設計時，必須充分考慮電場的均勻性，使極間及整個場域的電場分布盡可能均勻。本文采用比較簡便實用的有限元分析軟件Ansoft-Maxwell自帶的參數化和目標優化設計功能。Ansoft公司的Maxwell是一個功能強大、結果精確、易于使用的電磁場有限元分析軟件[5]。運用其強大的電場分析功能,對絕緣子的高低壓端的口徑、穿墻套管絕緣管體中部徑向安裝面板以及內六角螺絲沉頭直徑進行定性分析，進而實現對開關柜內部結構的優化設計，旨在使其內部電場分布盡可能均勻[6]。

1高壓開關柜電場計算理論基礎

高壓開關柜的電場計算是以有限元為理論基礎的。所謂的有限單元法(Finite-Element Method)，簡稱有限元法，是求解數值邊值問題以變分原理和剖分插值為基礎的一種數值計算方法[7，8]。在電磁場問題中，由于微分方程已知并且其微分方程可以通過對某個泛函的變分而得到。對于有多個自變量的函數φ(x,y,z)的泛函T(φ)來說，具有如下一般形式：

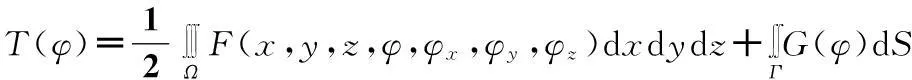
(1)

其數學依據是電場的拉普拉斯方程：

2φ=0,φ∈Ω

(2)

則在泛函極小的條件下，令δF=0,可得如下尤拉方程。

(3)

(4)

將由靜電場電位φ(x,y,z)構成的函數F及G，即：

(5)

G=-gφ

(6)

帶入式(2)式(3)可得：

(7)

Γ1φ=U0

(8)

上述三個式子分別是電磁場的泊松公式及第一類邊界條件和第二類邊界條件。可見它們與下面式(10)的泛函極值等價，即求電磁場的微分方程問題可化為求下述泛函求極小值的問題：

(9)

式中：φ為求解區域的電位。

用有限元技術，將式(10)由整體坐標轉換到局部坐標，從而得到有限元方程：

(10)

求解式(10)，即可得到區域中的電位分布。

2基于Maxwell高壓開關柜的優化

2.1　高壓開關柜電場仿真及優化設計步驟

a) Ansoft-Maxwell 3D的電場仿真操作流程如圖1 。

圖1　Ansoft仿真流程圖

b) Ansoft-Maxwell 3D的參數化和目標優化

Ansoft- Maxwell的優化設計由參數化分析(Parametric Analysis)和優化分析(Optimization)兩部分構成。使用優化器Optimetrics，用戶可以從眾多可行方案中找出一個最優解。

1) 參數化分析(Parametric Analysis)：定義一個或多個掃描變量，并給每個掃描變量定義取值范圍。優化器會在所有變量取值點進行計算，得到一系列的計算結果，這樣用戶就可以對結果進行比較，從而確定每個設計變量對最終設計性能的影響。流程如圖2所示。

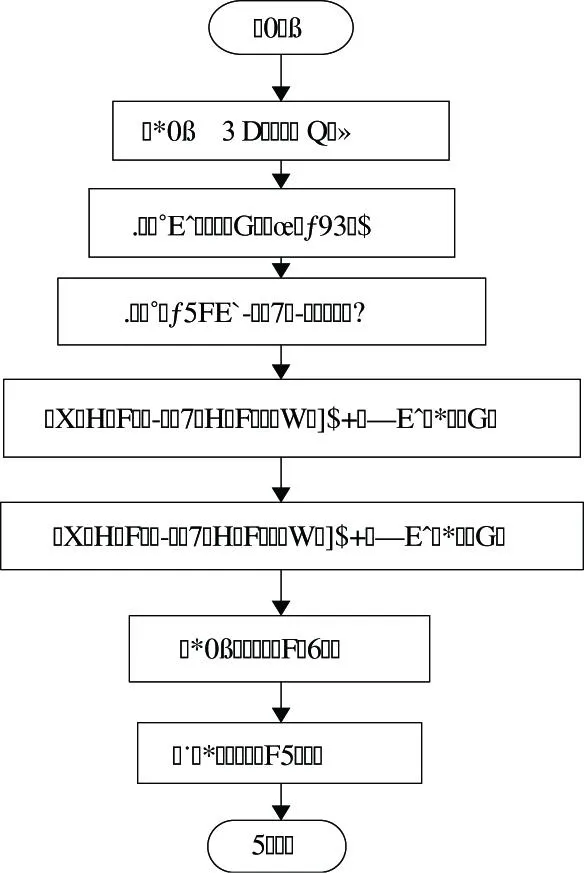
圖2　目標優化流程圖

2) 目標優化(Target Optimization)：先確定優化目標和成本函數，優化器通過優化設計參數值來滿足優化目標要求。采用連續非線性規劃的方法來進行優化。流程如圖3所示。

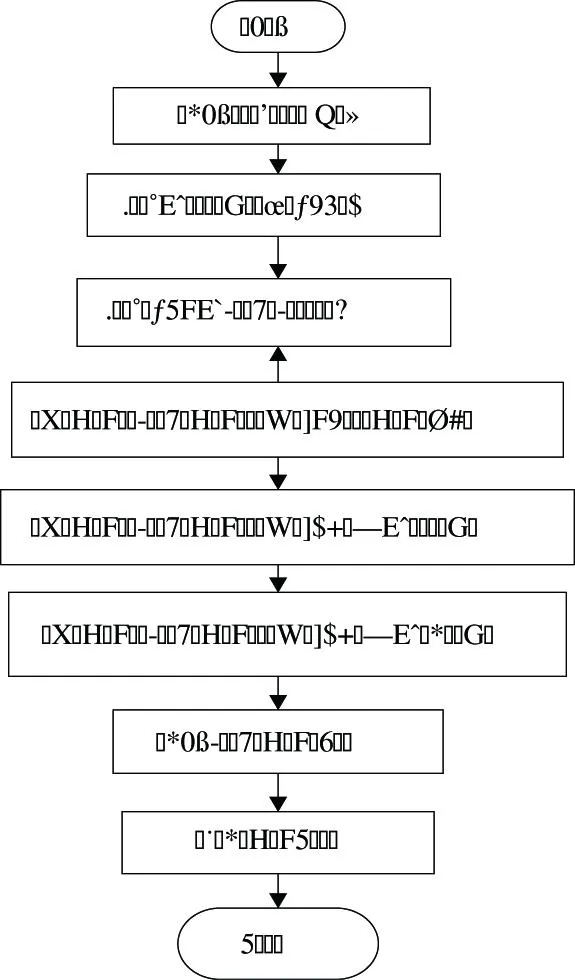
圖3　目標優化流程圖

2.2　絕緣子電場仿真及優化設計結果

絕緣子作為斷路器重要的支撐絕緣件，若沿面電場過大很容易發生沿面閃絡[9]。由于均勻電場作用主要通過外表面來實現，故可簡化其內部結構，將其簡化為近似圓柱狀，這樣不會對周圍裝置的電場強度造成影響，對其自身外表面的電場強度影響也很小，適合作為電場分析模型，絕緣子實際結構如圖4所示，簡化模型如圖5所示。高壓端和低壓端的直徑范圍均為30mm~80mm，材料屬性如表1所示，電場仿真結果如圖6所示。

圖4　實際結構

圖5　簡化結構

圖6　絕緣子電場仿真結果圖

表1　絕緣子材料屬性

絕緣子經參數化分析在低壓端為40mm時，電場值E隨高壓端直徑變化圖中獲得最優結果，如圖7所示。

圖7　絕緣子參數化最優結果

分析：經參數化分析，絕緣子在低壓端直徑為40mm時，當高壓端直徑為60mm，獲得最小的電場值1569.619V/m。

絕緣子目標優化的最優結果如圖8所示，在迭代至第30代得到最優值。

圖8　絕緣子優化結果折線圖

分析：在非線性規劃迭代第30代，絕緣子的低壓端直徑為40.01mm、高壓端直徑為63.44mm時，獲得最小的電

場值1549.6V/m。對比參數化結果和優化設計結果，兩者優化數據相近。

2.3　穿墻套管電場仿真及優化設計結果

穿墻套管也是非常重要的支撐絕緣件，其結構如圖9所示，內部需要穿過高壓銅導體，外邊緣的電位為0。因此其電場分布情況比較惡劣，穿墻套管具有近似軸對稱結構，工作條件也近似軸對稱。忽略螺絲孔和導體弧度，將模型簡化為4個圓柱嵌套，上下兩端是長方體，外圍為正六面體，簡化如圖10所示。穿墻套管中部徑向導體的安裝直徑范圍130mm~180mm。電場仿真結果如圖11所示，材料屬性如表2所示。

圖9　穿墻套管實圖

圖10　穿墻套管簡化圖

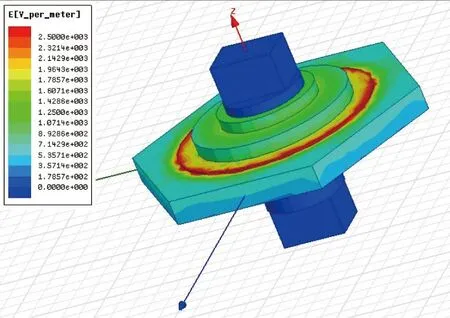
圖11　穿墻套管電場仿真圖

中部導體材料其余材料邊界材料銅環氧樹脂SF6

參數化分析的最優結果如圖12所示。

圖12　穿墻套管參數化結果折線圖

分析：經參數化分析，在穿墻套管的中部徑向直徑為175mm時，取得最優值，此時最小電場值5585.343V/m。

目標優化的最優結果如圖13所示，在第42代得到最優值。

圖13　穿墻套管優化結果折線圖

分析：在非線性規劃迭代第30代，穿墻套管的中部徑向直徑為177.41mm時，取得最優值，此時最小電場值5533.4V/m。對比參數化結果和優化設計結果，兩者優化數據相近。

2.4　螺絲電場仿真及優化設計結果

螺絲的分布非常廣泛，絕緣子附近所使用的內六角螺絲圓角較小，本節將對其電場強度進行分析。絕緣子附近的螺絲結構如圖14所示。因屏蔽作用，故螺絲內部將不再進行分析，主要分析表面電場強度。螺絲的材料為銅合金，根據內六角螺絲的規格表，將螺絲型號M3-M6簡化為模型1如15圖所示。內六角直徑范圍為2.5mm~5.2mm，將螺絲型號M8-M30簡化為模型2如圖16所示, 內六角直徑范圍為6mm~23mm。電場仿真模型如圖17和圖18所示。

圖14　螺絲實圖

圖15　簡化模型1

圖16　簡化模型2

圖17　簡化模型1電場仿真模型

圖18　簡化模型2電場仿真模型

螺絲型號M3-M6的簡化模型1經參數化分析的最優結果如圖19所示：

圖19　螺絲M3-M6參數化結果表格

分析：經參數化分析，對于簡化模型1來說，在螺絲內部直徑為3.75mm時取得最優值，此時最小的電場值3.11 e-9V/m。

螺絲型號M3-M6的簡化模型1目標優化的最優結果如圖20所示，在第20代得到最優值。

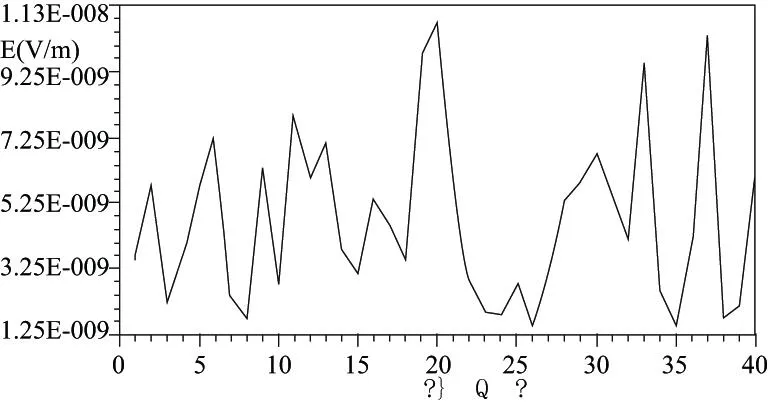
圖20　螺絲M3-M6參數化結果折線圖

分析：在非線性規劃迭代第20代，對于簡化模型1來說，螺絲內部直徑為3.04mm時，取得最優值，此時最小電場值1.72e-9V/m。對比參數化結果和優化設計結果，兩者優化數據相近。

螺絲型號M8-M36的簡化模型2經參數化分析的最優結果如圖21所示：

圖21　螺絲M8-M36參數化結果折線圖

分析：經參數化分析，對于簡化模型2來說，在螺絲內部直徑為22.5mm時取得最優值，此時最小的電場值3.13e-10V/m。

螺絲型號M8-M36的簡化模型2目標優化的最優結果如圖22所示，在第6代得到最優值。

圖22　螺絲M8-M36目標優化結果折線圖

分析：在非線性規劃迭代第6代，對于簡化模型2來說，螺絲內部直徑為22.79mm時，取得最優值，此時最小電場值2.31e-10V/m。對比參數化結果和優化設計結果，兩者優化數據相近。

3結語

通過分析高壓開關柜內部結構的電場分布，利用Ansoft-Maxwel自帶的兩種優化方法對其結構進行優化旨在得其使電場分布最均勻，經過分析，得出以下結論：

利用Maxwell 軟件自帶的參數化分析(Parametric Analysis)和目標優化分析(Optimization)兩種方法對絕緣子，穿墻套管和螺絲的結構進行優化分析，所得的優化結果相近。在軟件建模的基礎上進行變量的確定和與目標值的連接，使得結果更加直接準確。兩種優化功能互相補充和參考，為實際生產提供全面準確的信息。

參考文獻:

[1] 潘長明，劉剛，熊炬，等. 高壓開關柜絕緣事故的分析及防范措施[J]. 高壓電器，2011，47(7): 90-93.

[2] 張秀麗，賀勃，李擁軍，等. 高壓開關柜隔離觸頭壓力檢測值研究[J]. 高壓電器, 2009, 45(2): 94-96.

[3] 王宇. 10kV高壓開關柜事故分析及設計上的改進[J]. 科技信息2010,(21):994,1011.

[4] 陳健卯. 高壓開關柜絕緣事故原因及絕緣性能的優化措施[J]. 硅谷,2009,(12):19.

[5] 張洪信. 有限元基礎理論與ANSOFT應用[M]. 北京:機械工業出版社. 2005.

[6] Liu Xiaoming, Cao Yunong, Wang Erzhi. Optimization design of the contact and shield in vacuum interrupter based on the genetic algorithm. 19th ISDEIV,2000,463-466.

[7] 倪光正. 工程電磁場數值工程[M]. 北京.機械工業出版社，2004.2.

[8] 何紅雨. 電磁場數值計算法與MATLAB實現[M]. 武漢.華中科技大學出版社，2003.

[9] 于開坤，張冠軍，鄭楠，等. 真空中絕緣子閃絡前表面電荷分布的二維仿真[J]. 西安交通大學學報,2008,42(4):476-480.

Optimization of Electric Field in High Voltage Switchgear Based on Finite Element Method

DAI Jia-jia1, MIAO Hong-xia2

(1. College of Energy and Electrical Engineering, Hohai University, Nanjing 210098, China;

2. College of the Internet of Things Engineering, Hohai University, Changzhou 213022, China)

Abstract:Because the electric field intensity distribution of high voltage switchgear has an important influence on the insulating property, the research on its distribution is one of the most important tasks in high voltage technology. This paper simulates and models the electric field of 40.5 kv switchgear based on finite element method with ANSOFT-MAXWELL 3D and analyzes the distribution of the electrostatic field. The functions of parametric analysis and target optimization in MAXWELL are used to optimize the structure design of the high voltage switchgear and obtain the best average value of the electric field intensity distribution.

Keywords:high voltage switchgear； electric field intensity； optimization design

中圖分類號：TM591

文獻標志碼：B

文章編號：1671-5276(2015)02-0172-05

作者簡介：代佳佳(1990-)，女，山東泰安人，碩士研究生，主要研究方向為運動控制方向。

收稿日期：2014-11-15