分數階混沌系統的修正投影同步

孫振武

(上海電機學院 數理教學部, 上海 201306)

?

分數階混沌系統的修正投影同步

孫振武

(上海電機學院 數理教學部, 上海 201306)

摘要：介紹了分數階微分系統的微分變換數值解法；根據修正投影同步的原理以及分數階微分系統的穩定性特點，設計了分數階混沌系統的同步控制器；利用設計的控制器，實現了2個不同階超混沌系統之間的同步；用微分變換法對系統進行了數值仿真，仿真結果顯示兩系統已實現了投影同步，驗證了理論結果的有效性。

關鍵詞：修正投影同步; 分數階混沌; 微分變換法

由于混沌具有復雜的動力學結構，多年來一直是電子工程、信息處理和保密通信等多個領域的交叉研究熱點之一。20世紀90年代，Pecora等[1]首次實現了混沌的同步，打破了混沌不可控的傳統觀念，此后混沌同步問題得到了深入研究，取得了一系列成果。到目前為止，人們已經提出了多種混沌同步方案，如反同步[2]、廣義同步[3]、相同步[4]等。其中，投影同步指驅動與響應混沌系統軌道的振幅成某種比例關系[5]。如果兩者振幅的縮放比例因子為1，則為完全同步；若為-1，則為反同步。修正投影同步方法是讓驅動與響應混沌系統軌道的振幅保持為某一常數比例矩陣[6]。在混沌保密通信中，這種同步方法可以把數的二進制擴展到M進制，從而實現快速數字通信。

近年來，人們已將對混沌的研究延伸至對分數階混沌的研究[7-9]。分數階混沌不但秉承了整數階混沌的幾乎所有特點，再加上其具有歷史記憶效果、動力學過程與系統階次密切相關等特性，因此，它往往比整數階混沌具有更加復雜的動力學屬性，將其應用于保密通信中具有更高的安全性，在圖像處理、信息加密等領域具有更廣闊的應用前景。眾所周知，分數階微分系統的精確解是很難得到的，因此人們主要通過Adomian分解法[10]、Laplace分解法[11]、Adams-Bashforth-Moulton預報——校正法[12]、Homotopy分析法[13]等數值分析方法來對該類系統進行動力學分析。20世紀80年代，趙家奎[14]提出了對分數階微分方程進行數值分析的一種新方法——微分變換法，雖然它也是通過迭代的方法來求解的，但與傳統的泰勒級數方法不同，它不需要求系統的導數或偏導數，故需要的計算量被大大縮小，有效地提高了計算效率。本文根據分數階微分系統的動力學特性和混沌同步理論，研究兩個具有不同分數階的超混沌系統的修正投影同步，并采用微分變換法對設計的同步方案進行數值模擬仿真，以檢驗理論結果的正確性。

1分數微分變換法

考慮具有整數階初值條件、Caputo含義下的分數階微分系統

Dα(fi(t))=Ni[f(t)],fi(t0)=bi

(1)

式中，Ni[f(t)]為系統的線性和非線性部分，i=1,2,…,n；f(t)=(f1(t),f2(t),…,fn(t))；Dα(fi(t))為Caputo分數階微分算子，0<α≤1；t0為初始時刻；bi為fi(t)的初始值。人們常將式(1)寫成矢量形式

Dα(f(t))=N[f(t)],f(t0)=b

(2)

式中，b=(b1,b2,…,bn)。

文獻[14]中指出，

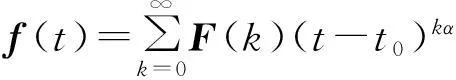
(3)

式中，F(k)為f(t)的分數階微分變換，

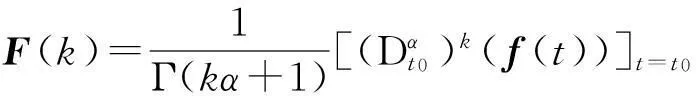
(4)

而

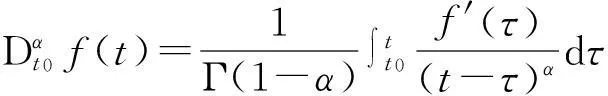
(5)

實際運算中，系統(1)的數值解常被約等于有限數列的和，即

(6)

部分分數階微分變換如表1所示[15-16]。

表1　分數階微分變換

根據表1中第4條的變換，可得到循環等式

F(k)=

(7)

式中，R為對式(2)中N[f(t)]實施分數階微分變換后得到的非線性算子。式(7)的解即是式(6)中的系數。實際計算中，先根據微分變換得到式(7)的解F(k)，然后代入式(6)中，即得到系統(1)的解。

對于微分變換法而言，計算區間t-t0越小，其解越精確。為此，常把實際計算區間[0,T]分割成M個小區間[tm-1,tm],m=1,2,…,M，每個小區間的寬度h=T/M。根據上述方法，對每個小區間[tm-1,tm]分別求解，即可得到每個小區間對應的解

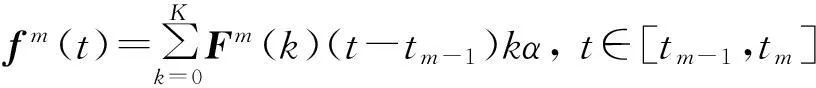
(8)

每一個小區間的初值條件可從前一個小區間的解中得到。

2分數階混沌的修正投影同步

假設驅動系統為

Dαx=f(x)

(9)

響應系統為

Dβy=g(y)+U(x,y)

(10)

式中，x,y∈Rn分別為驅動系統和響應系統的n維態矢量；x=(x1,x2，x3，x4);y=(y1,y2,y3,y4)；f,g： Rn→Rn是連續的非線性矢量函數，α、β為兩個系統的分數階；U(x,y)為本文設計的同步控制器。

定義1對于式(9)和(10)，若存在一個矩陣γ=diag(γ1,γ2,…,γn)，對任意的初始條件x(0)和y(0)，使得

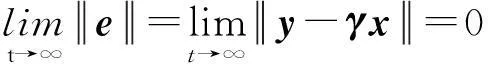
(11)

則兩系統就達到了修正投影同步。式中，γ為比例矩陣；e=(e1(t),e2(t),…,en(t))T為同步誤差；||·||為向量的范數。

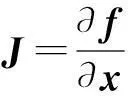
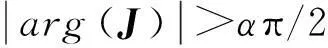
(12)

則該系統在該平衡點處漸近穩定。

為實現式(9)和(10)之間同步，把兩系統分解為

Dαx=Ax+W(x)

(13)

Dαy=By+G(y)+U(x,y)

(14)

式中，A、B∈Rn×n分別為驅動系統和響應系統線性部分的參數矩陣；W,G： Rn→Rn分別為兩系統的非線性部分。

把控制器U(x,y)也分成兩部分，即

U(x,y)=U1(x,y)+U2(x,y)

為實現兩系統之間的修正投影同步，令

(15)

式中，I為單位算子；K∈Rn×n為由常數組成的控制矩陣。

根據式(15)，響應系統式(14)可轉換為

Dαy=D(α-β)[Dβy]=

D(α-β)[g(y)+(D(β-α)-I)g(y)+U2(x,y)]=

g(y)+D(α-β)[U2(x,y)]=

g(y)+γ(A-B)x-G(y)+γW(x)-Ke=

By+γ(A-B)x+γW(x)-Ke

(16)

誤差系統為

Dαe=Dα[y-γx]=

By+γ(A-B)x+γW(x)-Ke-

γ[Ax+W(x)]=(B-K)e

(17)

選擇適當的控制矩陣K，使得(B-K)的本征值滿足不等式(12)，這樣，誤差系統式(17)漸近穩定，收斂于原點。根據定義1，式(9)、(10)實現了修正投影同步。

3兩個分數階四渦卷超混沌系統之間的修正投影同步

最近Dadras等[18]和Cang等[19]分別發現了一個具有復雜結構的四渦卷超混沌，本文中與其對應的分數階混沌分別是驅動系統和響應系統。現根據上文中提出的分數階混沌修正投影同步方案，實現這兩個不同分數階混沌之間的修正投影同步。

α=0.8,β=0.7,則響應系統為

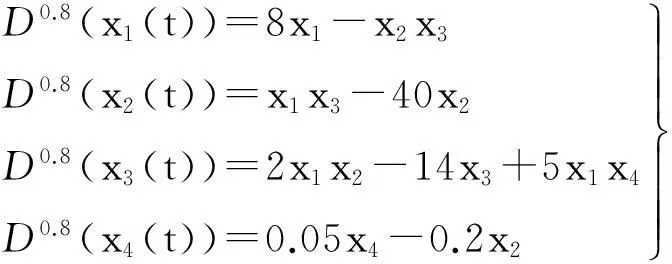
(18)

驅動系統為

(19)

式中，u1、u2、u3、u4為要設計的控制函數。

兩系統的同步誤差為

e1=y1-γ1x1,e2=y2-γ2x2，

e3=y3-γ3x3,e4=y4-γ4x4。

e=(e1,e2,e3,e4)T

其中，γi∈R(i=1,2,3,4)為比例因子。選取控制矩陣K為對角矩陣，K=diag(k1,k2,k3,k4)。根據設計的控制器式(15)，可得：

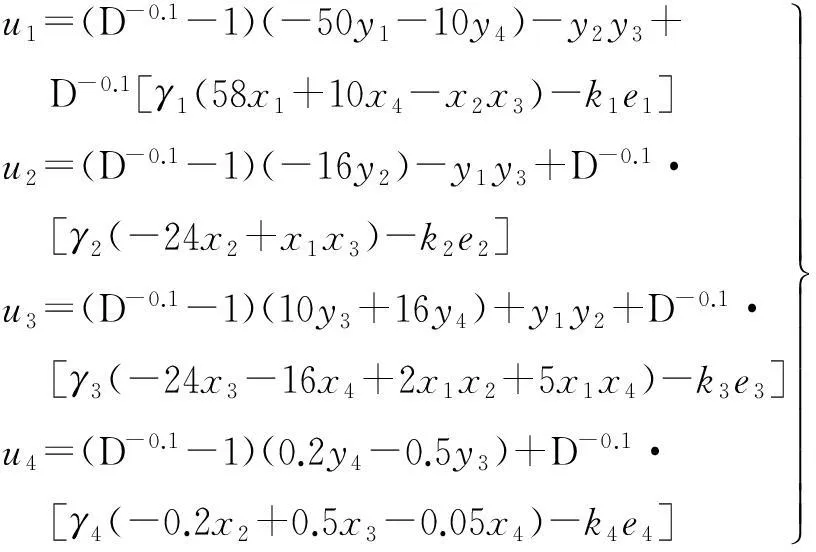
(20)

選擇控制矩陣為K=diag(5,5,15,5)，則可計算出誤差系統為

D0.8e=(B-K)e=

(21)

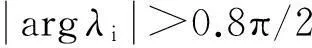
為驗證式(20)的有效性，本文利用分數階微分變換方法對驅動系統和響應系統進行數值模擬。其中，比例矩陣選擇γ=diag(-0.5,-0.5,-0.5,-0.5)，步長為0.001，驅動系統式(18)和響應系統式(19)的初始值x(0)、y(0)均選擇為(5,5,5,0.5)。模擬結果如圖1、2所示。

由圖1可見，驅動系統式(18)和響應系統式

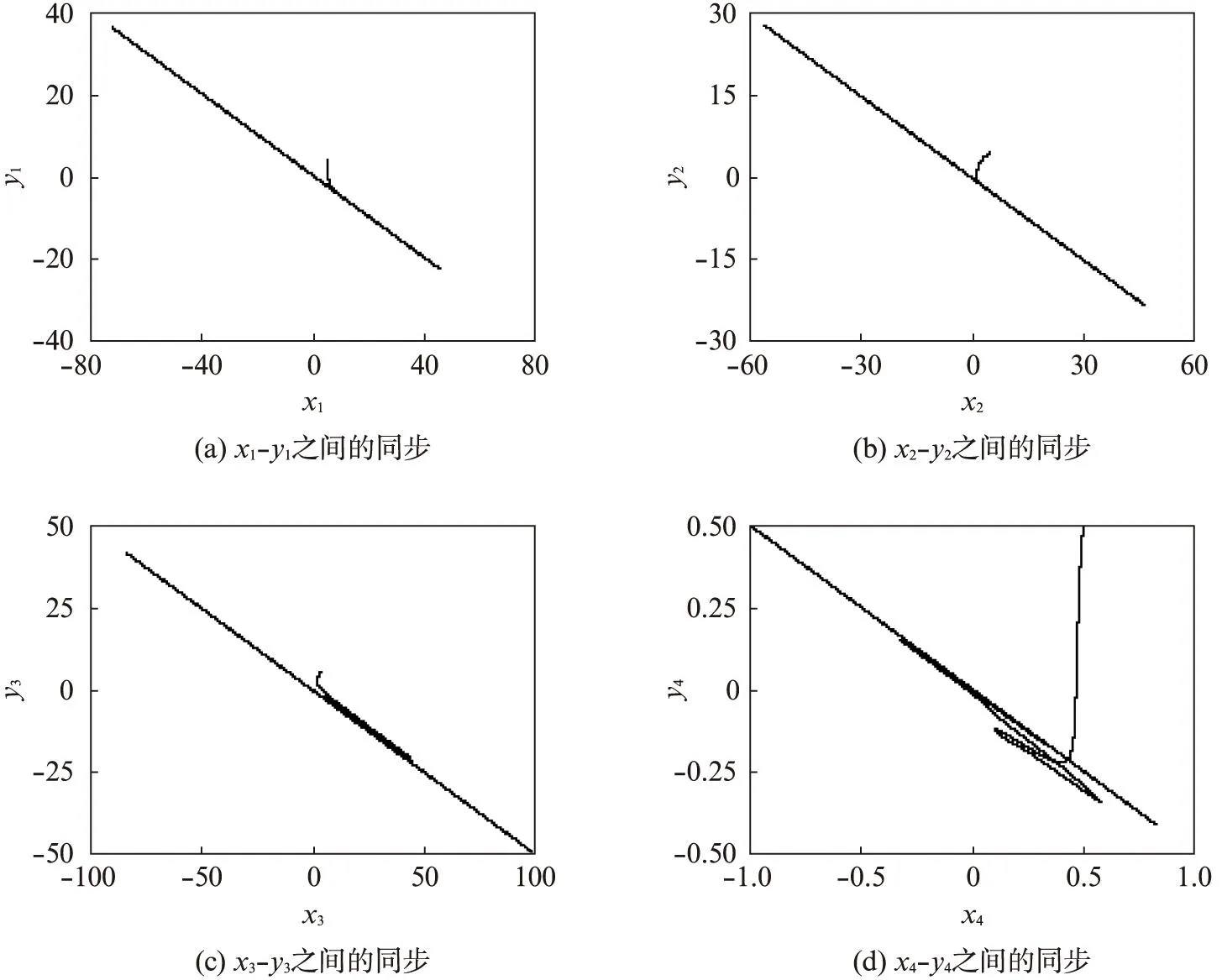
圖1　驅動系統(18)和響應系統(19)狀態量之間的修正投影同步Fig.1　Modified projective synchronization between the state vectors of the drive system (18) and the response system (19)

(19)按照投影系數γ=diag(-0.5，-0.5，-0.5，-0.5)已實現了同步，同步曲線呈反比例曲線，曲線上的“毛絮”為初始階段造成的。由圖2可見，響應系統(19)的吸引子根據驅動系統(18)的吸引子同比例縮小了1/2，這直觀地驗證了兩個分數階混沌確實實現了同步。

圖2　驅動系統(18)和響應系統(19)的混沌吸引子Fig.2　Chaotic attractors of the drive system (18) and the response system (19)

4結語

本文利用混沌的修正投影同步的原理以及分數階微分系統的穩定特點，設計了同步控制器，根據設計原理，實現了兩個不同階分數階超混沌系統之間的修正投影同步；利用分數階微分變換方法，對系統進行了數值仿真。仿真結果顯示，兩個分數階超混沌系統已實現投影同步，驗證了理論結果的有效性。

參考文獻：

[1]Pecora L M,Carroll T L.Synchronization in chaotic systems[J].Physical Review Letter,1990,64(8)： 821-824.

[2]Li G H.Synchronization and anti-synchronization of Colpitts oscillators using active control[J].Chaos,Solitons & Fractals,2005,26(1)： 87-93.

[3]Li S Y, Ge Z M.Generalized synchronization of chaotic systems with different orders by fuzzy logic constant controller[J].Expert Systems with Applications,2011,38： 2302-2310.

[4]Santoboni G,Pogromsky A Y,Nijmeijer H.An observer for phase synchronization of chaos[J].Physics Letters.A,2001,291(4)： 265-273.

[5]Wu Xiangjun,Lu Hongtao.Generalized projective synchronization between two different general complex dynamical networks with delayed coupling[J].Physical Letters.A,2008,374(38)： 3932-3941.

[6]Bai Jing,Yu Yongguang,Wang Sha,et al.Modified projective synchronization of uncertain fractional order hyperchaotic systems[J].Communications in Nonlinear Science Numerical Simulation,2012,17： 1921-1928.

[7]Letellier C,Aguirre L A.Dynamical analysis of fractional-order R?ssler and modified Lorenz systems[J].Physics Letters A,2013,377(28/30)： 1707-1719.

[8]Razminia,Torres D F M.Control of a novel chaotic fractional order system using a state feedback technique[J].Mechatronics,2013,23(7)： 755-763.

[9]Zhou Ping,Huang Kun.A new 4-D non-equilibrium fractional-order chaotic system and its circuit implementation[J].Communications in Nonlinear Science Numerical Simulation,2014,19(6)： 2005-2011.

[10]Momani S,Odibat Z.Analytical solution of a time-fractional Navier-Stokes equation by Adomian decomposition method[J].Applied Mathematics Computation,2006,177(2)： 488-494.

[11]Dyke P.An Introduction to Laplace Transforms and Fourier Series[M].[S.L.]: Springer,1999：1-75.

[12]Diethelm K,Ford N J.Multi-order fractional differential equations and their numerical solution[J].Applied Mathematics and Computation,2004,154(3)： 621-640.

[13]He Jihuan.Homotopy perturbation method： A new nonlinear analytical technique[J].Applied Mathematics and Computation,2003,135(1)： 73-79.

[14]趙家奎.微分變換及其在電路中的應用[M].武漢： 華中理工大學出版社,1986： 1-156.

[15]Odibat Z M,Bertelle C,Aziz-Alaoui M A,et al.A multi-step differential transform method and application to non-chaotic or chaotic systems[J].Computers & Mathematics with Applications,2010,59(4)： 1462-1472.

[16]Caponetto R,Fazzino S.A semi-analytical method for the computation of the Lyapunov exponents of fractional-order systems[J].Communications in Nonlinear Science Numerical Simulation,2013,18： 22-27.

[17]Ahmed E,El-Sayed A M A,El-Saka H A A.Equilibrium points,stability and numerical solutions of fractional-order predator-prey and rabies models[J].Journal of Mathematical Analysis and Applications,2007,325(1)： 542-553.

[18]Dadras S,Momeni H R.Four-scroll hyperchaos and four-scroll chaos evolved from a novel 4D nonlinear smooth autonomous system[J].Physics Letters A,2010,374(11/12)： 1368-1373.

[19]Cang Shijian,Qi Guoyuan,Chen Zengqiang.A four-wing hyper-chaotic attractor and transient chaos generated from a new 4-D quadratic autonomous system[J].Nonlinear Dynamics,2010,59(3)： 515-527.

Modified Projective Synchronization of Fractional-Order Chaotic Systems

SUNZhenwu

(Department of Mathematics and Physics Education, Shanghai Dianji University,

Shanghai 201306, China)

Abstract：Fractional differential transform method is introduced. Based on the principle of modified projective synchronization and the stable property of fractional system, a synchronization control is proposed. Synchronization of two non-identical fractional-order hyper-chaotic systems is realized by the control. The synchronization is simulated with differential transform methods. The results show that projective synchronization between the systems is indeed realized, showing effectiveness of the theoretical results.

Key words：modified projective synchronization; fractional-order chaos; differential transform method

文獻標志碼：A

中圖分類號：TP 391

文章編號2095 - 0020(2015)06 -0325 - 06

作者簡介：孫振武(1967 -)，男，教授，博士，主要研究方向為非線性科學與復雜系統，E-mail： sunzw@sdju.edu.cn

收稿日期：2015 - 06 - 29