Diophantine方程x3+8=397y2的整數(shù)解

李潤琪

(德宏師范高等專科學校數(shù)學系，云南 芒市 678400)

Diophantine方程x3+8=397y2的整數(shù)解

李潤琪

(德宏師范高等專科學校數(shù)學系，云南 芒市 678400)

摘要：利用遞歸序列、同余式、Maple小程序、Pell方程的解的性質證明了Diophantine方程x3+8=397y2僅有整數(shù)解(x,y)=(-2,0)．

關鍵詞：Diophantine方程；整數(shù)解；同余式；遞歸序列; Maple小程序

方程

x3+8=Dy2(x,y∈N,D>0，且無平方因子)

(1)

是一類重要的Diophantine方程，其整數(shù)解已有不少人研究過．1981年文[1]證明了D不能被3或6k+1型素因子整除時，如果D≡0,2,3(mod4)，則方程x3+8=Dy2僅有整數(shù)解；如果D≡11,19(mod20)，則方程x3+8=3Dy2無非平凡整數(shù)解；1991年文[2]給出了D含6k+1型素因子時方程x3+8=Dy2無非平凡整數(shù)解的一些充分條件；1992年文[3]給出了D含6k+1型素因子時，方程x3+8=Dy2無非平凡整數(shù)解的一些充分件．對于具體的D，文[4]-[8]已給出一些結果，但對于D=397時的情況至今沒有解決.本文主要研D=397時方程(1)的解的情況.

引理1[9]設p=3n(n+1)+1≡13(mod24)為奇素數(shù)，則不定方程x3+1=2py2無正整數(shù)解．

引理2[10]方程x4-3y2=1僅有整數(shù)解(x,y)=(±1,0)．

定理Diophantine方程

x3+8=397y2

(2)

僅有整數(shù)解(x,y)=(-2,0)．

證明：因為x3+8=(x+2)(x2-2x+4)，所以gcd(x+2,x2-2x+4)=gcd(x+2,(x+2)2-6(x+2)+12)=

gcd(x+2,12)=gcd(x+2,22×3)．

(3)

又794=2×397，而397=3×11×12+1，且397≡13(mod24)為奇素數(shù)，故由引理1知，方程(3)僅有整數(shù)解(x1,y1)=(-1,0)，故方程(2)在此情形下只有整數(shù)解(x,y)=(-2,0)．

當2?x時有2?(x+2)，因此gcd(x-2,2×3)=1或3，即gcd(x-2,x2+2x+4)=

=1或3，從而方程(2)得出下列4種可能的分解：

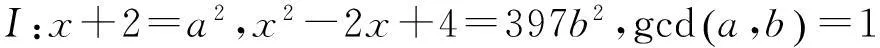
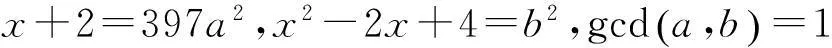
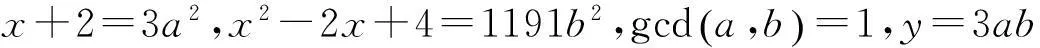
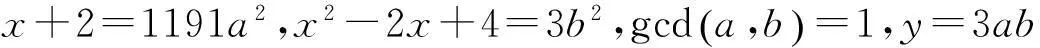
因為2?x，則x+2和x2-2x+4也為奇數(shù)，故a和b也為奇數(shù)，則a2≡1(mod8)，b2≡1(mod8)．

下面分別討論這4種情形下方程(2)的整數(shù)解的情況：

情形Ⅰ 由x+2=a2，得x=a2-2≡7(mod8)，代入x2-2x+4=397b2，得7≡x2

-2x+4=397b2≡5(mod8)，矛盾.故該情形下方程(2)無2?x的正整數(shù)解.

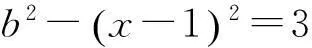
情形Ⅲ由x+2=3a2，得x=3a2-2≡1(mod8)，代入x2-2x+4=1191b2，得3≡x2-2x+4=1191b2≡7(mod8)，矛盾.故該情形下方程(2)無2?x的正整數(shù)解.

情形Ⅳ將x+2=1191a2代入x2-2x+4=3b2，整理得

b2-3(397a2-1)2=1

(4)

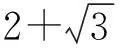
顯然b=±xn，397a2-1=±yn(n∈Z).因此397a2=±yn+1．又y-n=-yn，所以只需考慮：

397a2=yn+1

(5)

由(5)，得yn≡-1(mod397).

容易驗證下式成立：

yn+2=4yn+1-yn，y0=0，y1=1

(6)

下面對n進行討論：

對遞歸序列(6)取模397，得周期為396的剩余類序列，且僅當n≡199,395(mod396)時，yn≡-1(mod397)．所以(5)式要成立，需n≡199,395(mod396)，則需n≡1(mod2)．

對遞歸序列(6)取模2……