基于新型粒子群算法的散貨港口裝載機調度

李作志，王育靜

（天津工業大學 管理學院，天津 300387）

基于新型粒子群算法的散貨港口裝載機調度

李作志，王育靜

（天津工業大學 管理學院，天津 300387）

以散貨港口的裝載機為主要研究對象，在考慮車輛的速度、任務位置和運送路徑的基礎上，建立以最短時間為目標的車輛調度模型，對裝載車輛調度問題進行優化研究。在車輛調度優化方面，采用三維向量的編碼方式在一種新型的粒子群算法下對模型進行求解，證明算法的有效性，并且利用一種浮動的目標函數得以使裝載機的任務量均勻，以求得在實際運行中能幫助散貨港口提高工作效率、降低企業總體成本。

散貨港口；粒子群算法；裝載機調度

1 前言

港口的組成包括進出港口的航道、錨泊設施、通信導航設施、裝卸疏運設施、供應服務設施，其中貨物裝卸是港口最基本的功能，實現運輸方式的轉換，空間位置的有效轉移，從而開始或完成水路運輸的全過程。港口貨物的裝卸要利用港口裝卸機械設備，主要包括：起重機（門座式、高架式、龍門式等）、裝船機、裝載機、汽車吊、輪胎吊、拖車、卡車、叉車等，其中裝載機對于散貨港口來說更是重中之重，港口管理者越來越認識到裝載機調度的重要性，如何提高散貨港口裝載機的高效率和規范化作業，是一個亟待解決的問題。

目前國內外對港口車輛調度的研究大部分是利用遺傳算法進行優化，在粒子群優化算法上的研究并不深入。對于求解車輛調度問題，張維存等人利用主—從級遺傳算法建立以縮短顧客停留時間為目標的數學模型，研究了港口散貨物流鏟車調度的問題[1]；郝志莉等對港口物流中非滿載車輛運輸距離最短進行調度問題的研究，并利用遺傳算法對模型進行求解[2]。在優化粒子群算法方面的研究，姜燕、劉長民等人利用主—從式的粒子群算法在水文模型上進行了參數的優化，并且提出了基于粒子群算法的主從群洗牌演化(MSSE—PSO)的新型算法，提高了計算精度和效率[3]；吳聰等針對標準粒子群優化算法存在的不足，提出一種改進粒子群算法(IPSO)的物流配送車輛調度優化方法，并給出仿真實驗對其測試[4]；近期SabanGülcü,Halife Kodaz又提出了一種基于粒子群優化算法的并行算法（PCLPSO），通過對其他粒子群算法的比較測試，發現多個群的主—從式協同合作方式可以提高解決問題的質量和速度，對全局優化問題更加適用[5]。

綜上所述，對粒子群算法的優化是許多學者一直在努力的方向，在港口車輛調度中多注重所有車輛的研究，用遺傳算法求解也是按照傳統的方式進行。通過本文的研究，以裝載機為例建立可以實際運用到港口車輛調度的優化模型，并利用新型粒子群算法求解模型，通過加強對裝載機的管理，以期提高港口散貨物流的管理水平、運作效率和服務水平。

2 粒子群算法

2.1 標準粒子群算法

粒子群算法(Particle Swarm Optimization，簡稱PSO) 由Kennedy和Eberhart博士于1995年提出，基本概念源于對鳥群捕食行為的研究。群體在D維解空間上搜尋全局最優解，并且每個粒子都有一個適應函數值和速度來調整它自身的飛行方向以保證向食物的位置飛行，在飛行過程中，群體中所有的粒子都具有記憶的能力，能對自身位置、自身經歷過的最佳位置（pbest）和種群中最好的粒子位置（gbest）學習，最終接近食物的位置。圖1給出粒子速度和位置在第t代和第t+1代的調整示意圖，全局最優解在處。

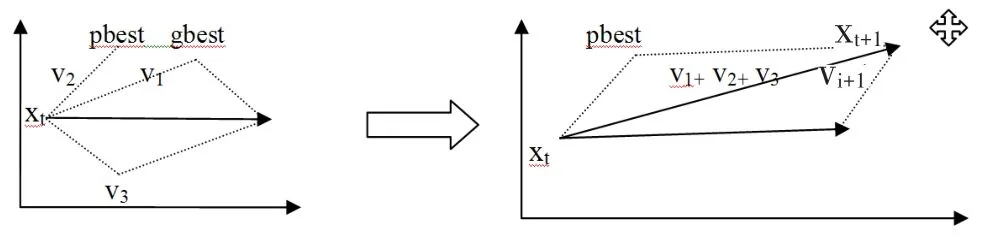
圖1 粒子速度和位置調整示意圖

圖中：t—迭代的時刻；

t+1—下一迭代時刻；

v1—“社會經驗”學習引起粒子向gbest方向飛行的速度；

v2—“自身經驗”學習引起粒子向pbest方向飛行的速度；

v3—粒子自身具有的速度。

標準粒子群算法的數學描述，假設搜索空間為D維，種群規模為N，第i個微粒個體所處位置為Xi=(xi1,xi2,...,xid)，每個個體的飛行速度為Vi=(vi1,vi2,...,viD)，個體經歷過的位置可定義為Si=(si1,si2,...,siD)，第i個粒子截至目前搜索到的最優位置為Pi=(pi1,pi2,...,piD)，整個粒子群迄今為止經過的最優位置為Pg=(pg1,pg2,...,pgD)。所以可以定義為，每個粒子的位置變化可以用如下公式進行表示：

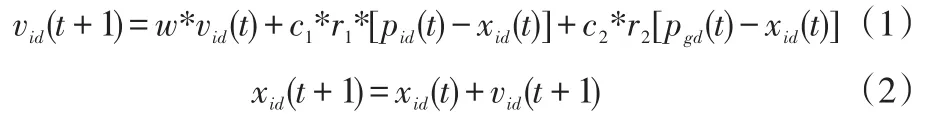
式中：t—當前粒子進化代數；

w—慣性因子，非負數，是控制速度的權重；

c1、c2—加速系數；

r1、r2—介于［0,1］之間的隨機數。

2.2 新型的粒子群算法

標準的粒子群算法雖然應用比較廣泛，但是也存在一些缺陷，比較明顯的有兩點：其一，是收斂速度慢；其二，是容易陷入局部最優化。本文經過對該算法資料的大量收集與研究，對其進行了一定的改善，以達到滿足實際車輛調度的應用。

基于種群互惠共生和共棲的思想，考慮到多群體協同進化，設計出一種新型粒子群算法模型，在該模型中利用一個主（master）—從（slave）式的結構來模擬共生群體之間的關系。整個種群被分為Z個子群（共生群體），其中Zm為主群（master swarm）數，Zs為從群（slave swarm）數，每個子群均包含相同的個體數，在搜索過程中各子群獨立進化負責在解空間中全局廣度搜索，而主群根據其共生群體（從群或其他主群）的經驗負責局部精確搜索，共生群體間的信息傳遞，在一定程度上避免了個體信息誤判造成的陷入局部最優的危險[6]。

根據不同的主、從群數設置，可以表示不同共生模式，本文以Zm∈[1,Z)，ZS=Z-Zm為例，即部分個體參與信息交流的共棲模式，來說明主-從式粒子群算法的計算原理。對種群進行分群后，每一個從群在迭代過程中利用標準的粒子群算法獨立更新速度和位置，在狀態更新之前把它們迄今為止發現的pbest發送給某一主群，此主群根據獲得的所有pbest及其他主群中最好個體信息進行速度和位置的更新，更新方程如下：

式中：M—主群；

以上方程是一種協作型的主—從式粒子群算法，在這種更新機制中，主群中的每個粒子根據自己的經驗，自身群體中其他粒子的經驗，再加上從群中的最好經驗進行速度和位置更新，通過多方考慮在一定程度上避免了陷入局部最優化。

3 裝載機調度的數學模型

3.1 問題描述

經調查得知，港口車輛調度存在以下問題：調度基本處于人工方式，有很多不完善之處；車輛載貨行駛至相應任務目標位置后空載返回；在實際港口裝卸作業中，來港船只所裝卸貨物不可能正好是裝卸車輛滿載的整數倍，可能造成車輛非滿載行駛的資源浪費。本文在以上問題的基礎上，利用新型粒子群算法對港口裝載車輛進行合理的調度，為每個任務選擇最合適的裝載車輛，為裝載車輛選擇最合適的行駛路線，以及滿足車輛最佳的裝載順序，以達到充分的利用資源，提高效率節約成本的目的。

3.2 前提假設

（1）車輛調度剛開始時，所有的裝載機都可使用，所處位置為車庫；

（2）裝載機完成一次任務后就停在任務目標位置，新任務的起始位置就是上一任務目標位置，所有任務完成后車輛返回車庫；

（3）堆場和泊位的位置及相關信息已知；

（4）泊位卸船的貨物優先級相同，無先后之分；

（5）每條路徑均順暢，不會產生交通堵塞和擁擠等情況。

3.3 數學模型

根據散貨港口的實際情況，本文著重以在船舶裝卸過程中每輛裝載機行駛總時間T最小為目標對裝載機進行調度，建立裝載機調度的優化模型如下：

（1）決策變量：Pjkab，Qjkbc

（2）目標函數：

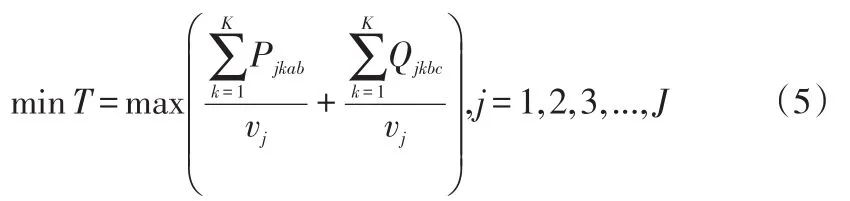
（3）約束條件：

（4）變量描述：j港口裝載機編號(j=1,2,...,J)；k等待裝卸的任務編號(k=1,2,...,K)；a裝載機當前位置(a=1,2,...,A)；b需要裝卸的任務位置(b=1,2,...,B)；c裝卸任務的目標位置(c=1,2,...,C)；vj裝載機j的速度，vj∈(0,45)；Pjkab第k個任務由第j輛裝載機從當前位置a到任務位置b的距離；Qjkbc任務位置b到任務目標位置c的距離。

上述目標函數（5）表示任務過程中裝卸車輛行駛的時間，包括兩部分：一是第k個任務由第j輛裝載機從當前位置a到達任務位置b所用時間；二是任務位置b到任務目標位置c所用時間。關于裝載機、任務位置及任務目標位置的確定，是通過裝載機的車載設備讀取，當位置確定后它們之間的距離也就確定了。調度的目的是求這兩部分行駛時間最短，每次迭代以用時最長的那輛裝載機任務為目標函數，此時目標函數是變動的，即哪個裝載機用時長就優化哪個，從而使任務整體的運輸時間最優。

在上述約束條件中，式（6）表示對裝載機的調度必須滿足完成所有裝卸任務；式（7）表示所有裝卸任務之間的距離不小于零；式（8）表示裝載機新任務的起始位置就是上一任務的目標位置；式（9）表示第j輛裝載機所用時間與第j+1輛差的絕對值小于ξ，目的是讓每個裝載機的任務執行時間均衡。

4 裝載機調度問題的算法實現

4.1 粒子的編碼和解碼

裝載機調度問題模型建立以后，面臨著兩大問題需要解決，一是將裝載機分配到裝卸任務位置，二是各裝載機與裝卸任務的順序安排。根據裝載機調度問題的基本思路，提出了新型粒子群算法即主-從式的粒子群算法來求解該調度問題。假設裝卸任務總數為K，裝載機總數為J，構建一個粒子長度為K的三維粒子，其中第一維表示裝卸任務；第二維表示裝載機任務分配；第三維表示裝載機作業順序。三維粒子的表示方法見表1。

表1 三維粒子的編碼

在上述三維粒子表示中，粒子位置向量xjk被限制在[1，J+ 1）的范圍內，考慮實際情況對于裝載任務k所對應的粒子位置向量xjk進行取整，即操作函數為INT（xjk），INT（xjk）∈[1,J]，可知，裝載任務k就由裝載機INT（xjk）來完成，這樣就得到J輛裝載機在各裝載任務K上的分配方案，對于車輛j的作業順序，解碼時通過yjk的大小對同一裝載機的任務按照編號進行粒子向量從小到大排序，從而確定裝載機的作業順序，通過以上解碼可得到調度問題的一個解。由此可見，通過以上操作就可以在粒子位置與調度問題解之間建立映射關系，如圖2、圖3所示。

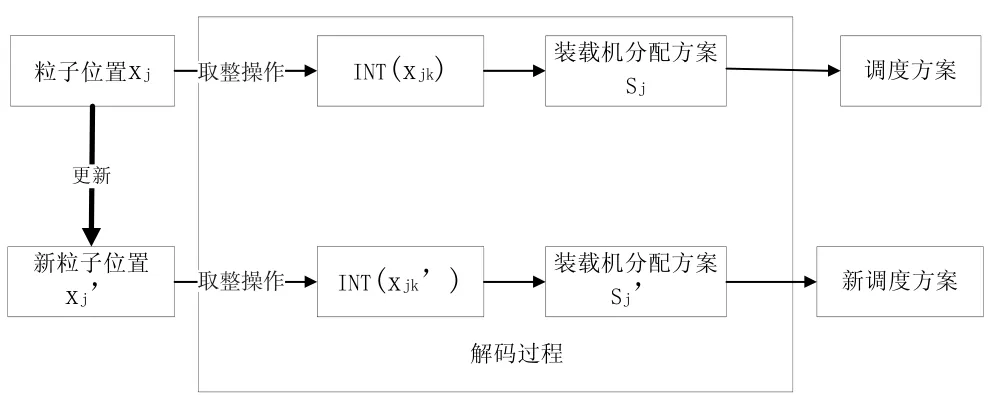
圖2 粒子位置與裝載機任務分配的映射更新關系

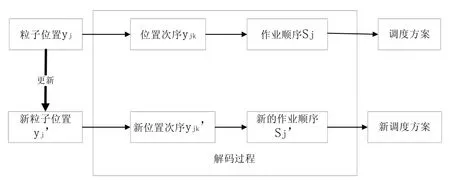
圖3 粒子位置和裝載機作業順序的映射更新關系

從上述表示方法中，可以看出粒子位置與調度解的映射關系解碼過程很簡單，在實際應用中需要在算法的初始階段對生成的初始方案進行判斷，如果有不滿足現實調度情況的粒子就重新初始化該粒子。

4.2 新型粒子群算法的偽代碼

針對前面的新型粒子群算法[6]，利用MATLAB7.14 (R2012a)運行環境進行算法流程的編制，其中新型粒子群算法的偽代碼如下：

5 實例仿真及分析

5.1 數據來源

為更好的驗證新型粒子群算法的有效性和MATLAB編制程序的可行性，下面對散貨港口中的裝載機調度進行動態的仿真實驗。粒子群算法的粒子數為20，為了更好的優化結果，在先前研究者的基礎上，對初始參數進行設置：學習因子c1= c2=2.05，c3=2；慣性權重的設置是線性下降的，隨著迭代次數的增加從0.9下降到0.4；實驗中總子群數Z=4，即其中主群Zm=1，Zs=3，是共生群體的規模；最大迭代次數為200次。仿真對象為：4個裝卸任務，3輛裝載機，裝載機在廠區行駛速度小于50km/h，每個任務的位置、任務的目標位置及裝載機的位置和速度通過車載設備傳輸到港區的數據回傳系統當中，采集數據獲得信息，位置信息用坐標表示，港區在（100，100）范圍內，圖上1cm代表實際50m。在進行車輛的調度中，除了需要考慮裝載機和任務的位置之外，還要考慮裝載機在調度時是否在作業中，以及作業時間。以下表2、表3是仿真所需要提供的數據。

表2 港區裝載機的行駛速度

表3 數據采集獲得的相關數據

表中坐標位置已知，裝載機車庫的位置編號0坐標為（40，54），假設兩個坐標分別為（a，b）和（c，d），可得兩個位置的距離為：D= (a-c)2+(b-d)2。所有裝卸任務和任務目標位置的平面分布如圖4所示。

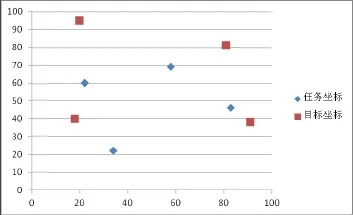
圖4 裝卸任務和目標位置的平面分布圖（單位：cm）

5.2 結果分析

仿真實驗中首先驗證了新型粒子群算法比標準的粒子群算法的優越性，在同一臺計算機上用同一MATLAB版本進行多次計算,發現新型的粒子群算法有著較快的收斂速度和求解精度，這一點從圖5迭代200次的結果可以看出。而從計算結果還可知，最優車輛調度方案為：

裝載機1：0→1→1’→0

裝載機2：0→2→2’→3→3’→0

裝載機3：0→4→4’→0

經過多次計算求得裝載機調度問題的最優方案所用時間是0.76h，最優函數值隨函數迭代次數變化的曲線如圖5所示。從圖5中可以明顯看出，采用本文所提出的新型粒子群算法能夠快速準確的求出三維粒子群編碼的車輛調度問的最優方案，并且搜索到最優值的效率和準確度都優于標準粒子群算法，因此為求解港區裝載機問題提供了一種新的方法。

Study on Loader Deployment in Bulk Harbors Based on Innovative PSO

Li Zuozhi,Wang Yujing
(School of Management,Tianjin Polytechnic University,Tianjin 300387,China)

In this paper,with the loading machines at the bulk harbors as the object,and on the basis of the consideration of the vehicle speed,task location and transport route,we built the vehicle dispatching model aiming at the shortest operation time,solved it using a newly developed PSO,which proved the validity of the algorithm,and at the end,used a floating objective function to spread out the task volume of the loading machines to improve the operational efficiency of the ports and reduce their overall costs.

bulk harbor;PSO;loading machine deployment

U653.923

A

1005-152X(2015)11-0130-04

10.3969/j.issn.1005-152X.2015.11.036

2015-09-28

李作志（1975-），男，天津人，天津工業大學管理學院副教授，主要研究方向：管理科學與工程、資源經濟及管理；王育靜（1991-），女，山東濟南人，天津工業大學管理學院碩士研究生，主要研究方向：物流工程。