關(guān)于“關(guān)于克勞修斯等式證明的再討論”的討論

蔣小勤

(海軍工程大學(xué)應(yīng)用物理系，湖北 武漢　430033)

教學(xué)經(jīng)驗(yàn)交流

關(guān)于“關(guān)于克勞修斯等式證明的再討論”的討論

蔣小勤

(海軍工程大學(xué)應(yīng)用物理系，湖北 武漢430033)

摘要指出“關(guān)于克勞修斯等式證明的再討論”一文論證過程中存在的問題，提出了一種在相鄰卡諾循環(huán)之間過渡的循環(huán)路徑，并證明了用若干個(gè)卡諾循環(huán)逼近任意可逆循環(huán)的可行性及其等價(jià)性。本文的研究支持主流熱學(xué)教材中“用若干個(gè)完整的卡諾循環(huán)去分解任意循環(huán)，相鄰的兩個(gè)卡諾循環(huán)之間的重疊部分在兩次循環(huán)中相互抵消”的論證方法。但現(xiàn)行教材的論述過程確實(shí)存在過于簡略、不夠嚴(yán)謹(jǐn)?shù)膯栴}，本文在闡明用卡諾循環(huán)分解任意循環(huán)的“等效性”內(nèi)涵的基礎(chǔ)上，采用泰勒級數(shù)展開及極限理論等高等數(shù)學(xué)方法，完善了克勞修斯等式的證明過程.

關(guān)鍵詞克勞修斯等式；卡諾循環(huán)；任意可逆循環(huán)；可逆過程

REVIEW “ON THE PROOF OF CLAUSIUS EQUALITY (CONTINUED)”

Jiang Xiaoqin

(Department of Applied Physics, Naval University of Engineering, Wuhan, Hubei 430033)

AbstractSeveral problems occurred in the argumentation process of the paper “On the Proof of Clausius Equality (Continued)” have been pointed out. One kind of cycling path serving as a transition among neighboring Carnot cycles has been proposed. The feasibility and equivalence of approaching arbitrary cycle by several Carnot cycles has been proven. This article stands with the argumentation method for dividing arbitrary cycle by several complete Carnot cycles, where the overlapping part between neighboring Carnot cycles are neutralized due to the opposite loop directions, in main stream thermal physics textbooks. But it is a real fact that the proof procedure in textbooks is too sketchy and rather loosely in mathematics. Using Taylor’s series and limit theorem, a complete proof of Clausius equality with the necessary process have been presented in this paper.

Key wordsClausius equality; Carnot cycle; arbitrary reversible cycle; reversible process

熵是熱力學(xué)系統(tǒng)的一個(gè)重要的態(tài)函數(shù)，熵的概念還被推廣到了現(xiàn)代信息學(xué)等領(lǐng)域中，備受廣大科技工作者的關(guān)注.工科大學(xué)物理課程將熵列入基本教學(xué)內(nèi)容.現(xiàn)行的熱學(xué)教材通常循著先介紹“卡諾循環(huán)”，再介紹“克勞修斯等式不等式”的路徑，自然地引入熵這個(gè)態(tài)函數(shù).然而由于在推導(dǎo)“克勞修斯等式不等式”這個(gè)環(huán)節(jié)，為了重點(diǎn)突出其物理意義，大多教材采用文字論述，沒有給出嚴(yán)格的數(shù)學(xué)證明過程.這就引發(fā)了物理教學(xué)工作者對這個(gè)問題的廣泛討論[1-3]. 最近《物理與工程》雜志上刊出的 “關(guān)于克勞修斯等式證明的再討論”一文[3](以下簡稱為“再討論”)認(rèn)為一些主流熱學(xué)教材中證明克勞修斯等式的做法，即“用若干個(gè)完整的卡諾循環(huán)去分解任意循環(huán)，認(rèn)為相鄰的兩個(gè)卡諾循環(huán)之間的重疊部分在兩次循環(huán)中相互抵消”的論證方法存在問題，并利用簡化的分解圖證明主流熱學(xué)教材中有關(guān)論證的問題在于“工作物質(zhì)無法在兩個(gè)相鄰的卡諾循環(huán)之間過渡”，進(jìn)一步指出“卡諾循環(huán)之間的重疊部分根本未曾被經(jīng)歷，并無‘抵消’之說”. 又一次將克勞修斯等式的證明問題提了出來.本文研討的問題是：

(1) 果然像“再討論”一文的論述那樣，主流的熱學(xué)教材都犯了同樣的錯(cuò)誤嗎？

(2) 如果熱學(xué)教材中有關(guān)論述定性上并沒有錯(cuò)，只是論證不夠嚴(yán)謹(jǐn)?shù)脑挘芊裢晟破湔撟C過程，并避免冗長的數(shù)學(xué)推導(dǎo)，保留清晰直觀的物理圖像，以便于在大學(xué)物理課程教學(xué)中運(yùn)用?

對問題(1)，本文提出了一種在相鄰卡諾循環(huán)之間過渡的循環(huán)路徑，并證明了用若干個(gè)微小卡諾循環(huán)逼近任意循環(huán)的可行性及其等價(jià)性.對問題(2)，本文提出了選取微小卡諾循環(huán)等溫線應(yīng)滿足的“等效性”條件，補(bǔ)充了必要的熱溫比積分計(jì)算過程，完善了克勞修斯等式的證明.

1任意可逆循環(huán)的卡諾循環(huán)分解

為了證明克勞修斯等式，即對于任意的可逆循環(huán)過程有

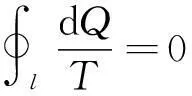
(1-1)

大學(xué)物理教材中常借用卡諾循環(huán)的性質(zhì)：

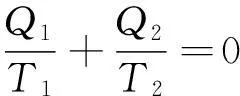
(1-2)

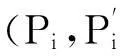
“……任意兩個(gè)相鄰的微小可逆卡諾循環(huán)總有一段絕熱線是共有的，但進(jìn)行的方向相反從而效果完全抵消，因此，這一連串微小的可逆卡諾循環(huán)的總效果就是圖中鋸齒形包絡(luò)線所表示的循環(huán)過程……”.從直觀看“如果使每個(gè)微小卡諾循環(huán)無限小，從而使卡諾循環(huán)的數(shù)目n→∞,則這鋸齒形路徑所表示的循環(huán)過程就將無限趨近于原來考慮的任意可逆循環(huán)過程”，進(jìn)而利用卡諾循環(huán)的性質(zhì)式(1-2)，直接得到克勞修斯等式(1-1)[4,5].對此有文獻(xiàn)[1,2 ]提出疑問，認(rèn)為這樣的論證不夠嚴(yán)謹(jǐn).這些文獻(xiàn)大都是從如何完善證明過程的角度展開分析與討論的.最近《物理與工程》上刊出的“再討論”一文則提出了“工作物質(zhì)無法在兩個(gè)相鄰的卡諾循環(huán)之間過渡”“卡諾循環(huán)之間的重疊部分根本未曾被經(jīng)歷，并無‘抵消’之說”的論斷，從更為基本的角度對主流教材中有關(guān)克勞修斯等式的證明方法提出質(zhì)疑[3].“再討論”一文認(rèn)為：“……這樣的陳述表明每個(gè)微小的循環(huán)都要完整地進(jìn)行(否則不能說它們相鄰的部分抵消)，但這樣立即會使過程陷入死循環(huán)……”, 進(jìn)而用簡圖(“再討論”一文之圖2)說明在完成第一個(gè)卡諾循環(huán)后系統(tǒng)回到了起點(diǎn),“……沒有辦法過渡到第二個(gè)循環(huán)從而走完全部鋸齒形包絡(luò)線”.“再討論”一文斷言“要讓系統(tǒng)無重復(fù)地經(jīng)歷所有鋸齒形包絡(luò)線，圖中的bg段必須不能被經(jīng)歷，……并無‘抵消’之說，……,中間所謂重復(fù)部分，均沒有實(shí)際經(jīng)歷過”.本文認(rèn)為“再討論”一文的這些觀點(diǎn)值得商榷.

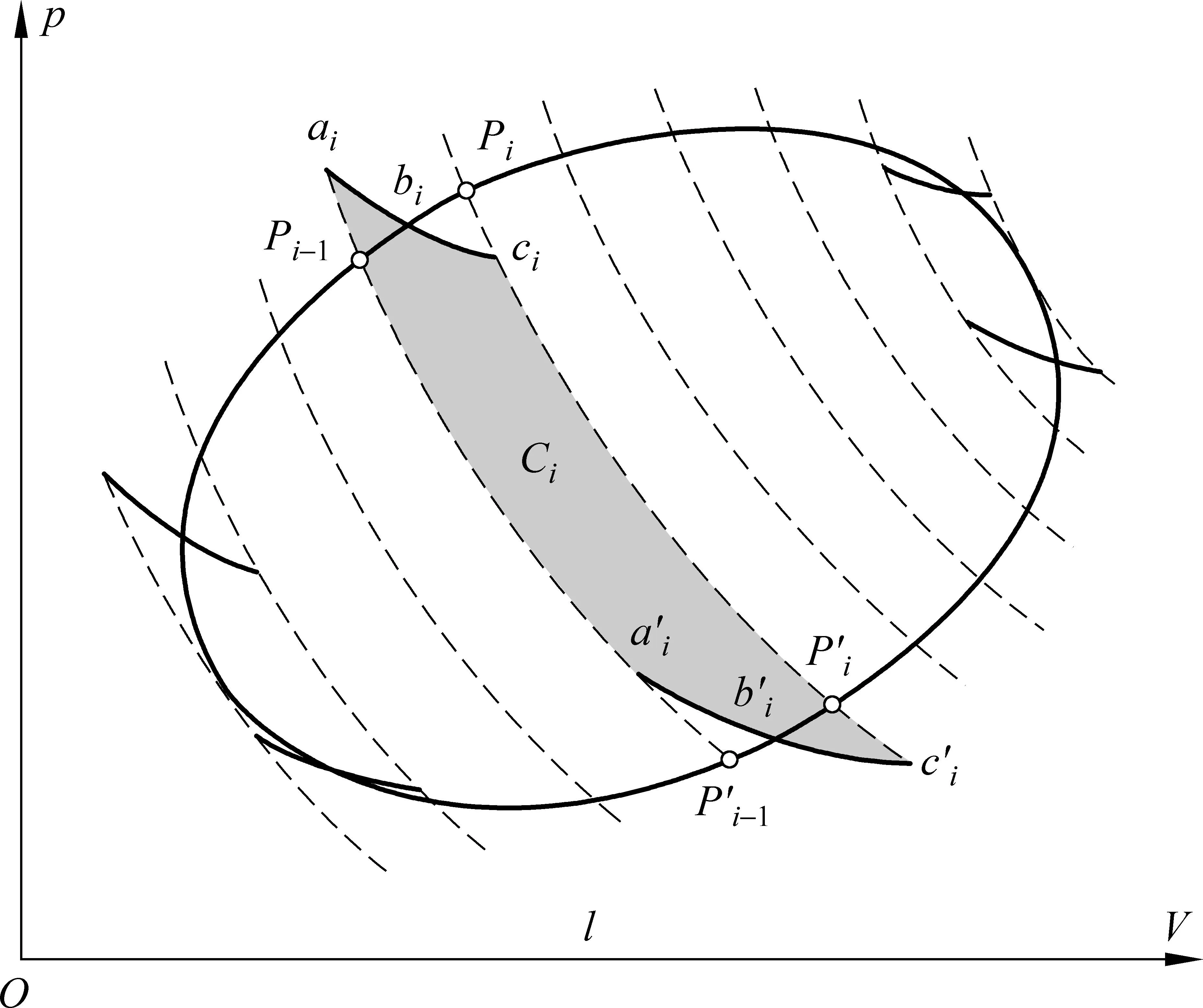
圖1　任意可逆循環(huán)l的卡諾循環(huán)分解示意圖圖中陰影區(qū)域代表第i個(gè)卡諾循環(huán)Ci

2卡諾循環(huán)分解的等效性

本文認(rèn)為教材中將任意可逆循環(huán)l分解為n個(gè)微小的卡諾循環(huán)是一種等效論證方法.這里要明確“等效”這個(gè)概念的含義，重要的是原任意循環(huán)l與n個(gè)微小的卡諾循環(huán)的總效果，而非系統(tǒng)經(jīng)歷循環(huán)路徑的細(xì)節(jié)，尤其對于可逆過程而言，正、逆兩次過程的效果為零.“再討論”一文之所以會得到“……沒有辦法過渡到第二個(gè)循環(huán)從而走完全部鋸齒形包絡(luò)線”的斷言，就源于“要讓系統(tǒng)無重復(fù)地經(jīng)歷所有鋸齒形包絡(luò)線,……”這個(gè)細(xì)節(jié)之上.其實(shí)如果某一段鋸齒形包絡(luò)線被多走了一個(gè)來回，其總的效果是互相抵消的.所以只要不拘泥于系統(tǒng)經(jīng)歷路徑的細(xì)節(jié)，而注重總的效果的話，就可以設(shè)計(jì)由n個(gè)卡諾循環(huán)構(gòu)成的循環(huán)過程來逼近一個(gè)任意可逆循環(huán)過程.本文用一個(gè)只包含4個(gè)卡諾循環(huán)的簡圖說明之(如圖2所示)，當(dāng)系統(tǒng)從P0點(diǎn)出發(fā)沿著第一個(gè)卡諾循環(huán)路徑C1回到起點(diǎn)P0后，繼續(xù)沿鋸齒路徑P0a1b1c1P1到達(dá)P1點(diǎn)，再沿著C2完成第二個(gè)卡諾循環(huán)……, 如此繼續(xù)，直到完成全部卡諾循環(huán)后系統(tǒng)到達(dá)Pn-1(圖2中的P3),再令系統(tǒng)從Pn-1沿鋸齒路徑逆向回到P0，此時(shí)系統(tǒng)經(jīng)歷過程的總效果與n個(gè)獨(dú)立的卡諾循環(huán)等效.進(jìn)一步，由于相鄰的兩個(gè)卡諾循環(huán)之間的重疊部分在兩次循環(huán)中相互抵消，則系統(tǒng)經(jīng)歷過程的總效果也與以這n個(gè)獨(dú)立的卡諾循環(huán)的外緣構(gòu)成的鋸齒路徑循環(huán)等效. 由此可見：“再討論”一文所謂的“陷入死循環(huán)”“……并無‘抵消’之說”“……中間所謂重復(fù)部分，均沒有實(shí)際經(jīng)歷過”，以及“……這樣容易使初學(xué)者產(chǎn)生誤解，……”等論斷都不能成立.

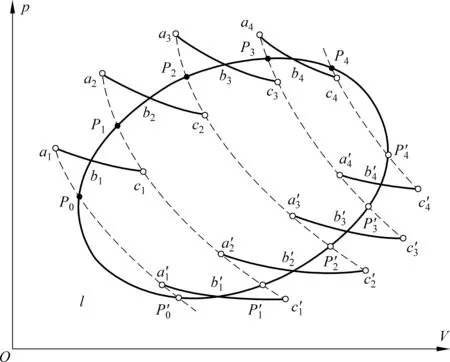
圖2　用4個(gè)卡諾循環(huán)分解任意可逆循環(huán)l的簡圖圖中是等溫線與循環(huán)l的交點(diǎn).

3克勞修斯等式的嚴(yán)格證明

由于教學(xué)對象不同，教材中有關(guān)克勞修斯等式不等式的證明方法也各不相同，例如文獻(xiàn)[6,7]采用費(fèi)米法，文獻(xiàn)[8]則以理想氣體為例，從微觀狀態(tài)數(shù)玻爾茲曼熵公式及熱力學(xué)第一定律推得

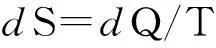
(3-1)

再由熵是狀態(tài)函數(shù)，推得任意可逆循環(huán)過程的克勞修斯等式(1-1).

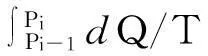
有關(guān)第一個(gè)步驟，對教材[8]中的表述：“當(dāng)小卡諾循環(huán)的數(shù)目趨向無窮大時(shí)，鋸齒形曲線就趨向原可逆循環(huán)……”,以及教材[9,10]中類似的表述，文獻(xiàn)[2]提出了異議，其主要觀點(diǎn)是，鋸齒形曲線的斜率與原循環(huán)回路l的不等、其長度也不同.本文作者認(rèn)為這里的分歧來自于對“趨向”一詞內(nèi)涵的理解上.如果把“趨向”理解為“全同”，就會出現(xiàn)文獻(xiàn)[2]指出的問題.但是，顯然這里的“趨向”一詞不能作“全同”來理解，而應(yīng)當(dāng)理解為數(shù)學(xué)上的“收斂”，物理上理解為循環(huán)效果的“等效”.

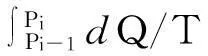
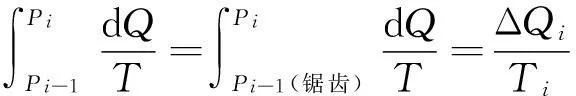
(3-2)

其中，Ti是小卡諾循環(huán)高溫等溫線的溫度，ΔQi是系統(tǒng)工質(zhì)與熱源Ti交換的熱量.同理得

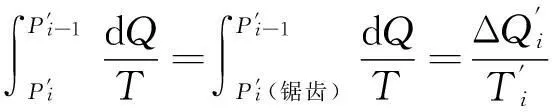
(3-3)

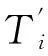
將沿任意可逆循環(huán)路徑l熱溫比的積分式寫成分段積分形式

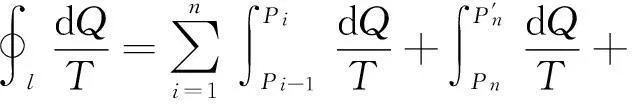
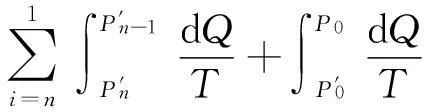
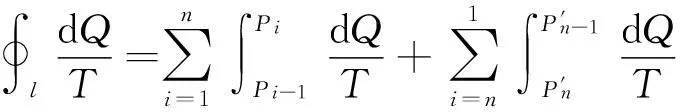
(3-4)

將式(3-1)、式(3-2)代入式(3-4)得

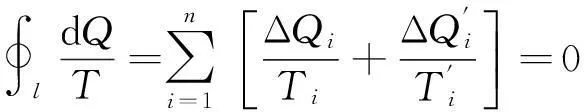
(3-5)

這就證明了克勞修斯等式.這里運(yùn)用了卡諾循環(huán)的性質(zhì)式(1-2)，即

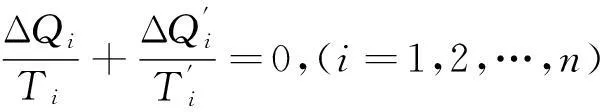
(3-6)

如果不采用“等面積法”選取微小卡諾循環(huán)的等溫線，將熱力學(xué)第一定律ΔQ=ΔU+A運(yùn)用于由l上微元(Pi-1,Pi)與鋸齒路徑(Pi-1aibiciPi)圍成的閉合循環(huán)(ΔU=0),則有

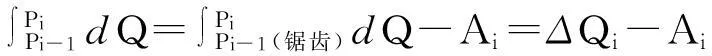
(3-7)

其中，Ai=SΔPi-1aibi-SΔbiciPi是在循環(huán)過程(Pi-1aibiciPibiPi-1)中系統(tǒng)對外輸出的凈功，由于與ΔQi相比Ai是高階無窮小量[11]，所以有

(3-8)

對系統(tǒng)在微元(Pi-1,Pi)范圍內(nèi)的溫度T(p,V)，在等溫線與l的交點(diǎn)bi(pi,Vi)處作泰勒級數(shù)展開，取線性近似為

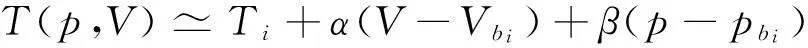
(3-9)

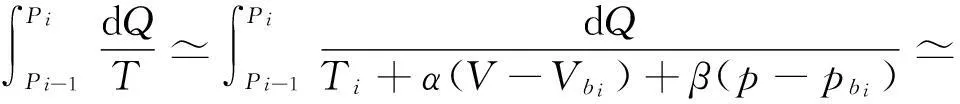
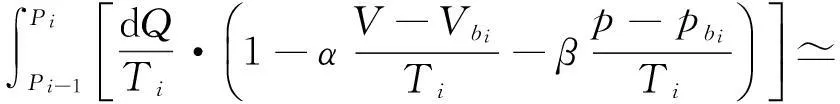
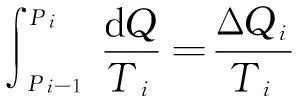
(3-10)

可見，只要微小卡諾循環(huán)的等溫線與原任意循環(huán)l在(Pi-1,Pi)微元上相交于bi,即使曲邊三角形ΔPi-1aibi與ΔbiciPi的面積不相等，式(3-2)與式(3-3)在n→∞的極限意義下仍然嚴(yán)格成立.“等面積法” 是眾多可能的等溫線取法中的一種，并不是必須的.但由于等面積法的物理概念直觀明了，數(shù)學(xué)推導(dǎo)過程形式簡單，因而被廣為采用.

4結(jié)語

綜合以上分析可見：

(1) 主流熱學(xué)教材中“用若干個(gè)完整的卡諾循環(huán)去分解任意可逆循環(huán)，相鄰的兩個(gè)卡諾循環(huán)之間的重疊部分在兩次循環(huán)中相互抵消”的論證方法原則上是可行的，并不存在“再討論”一文列舉的問題.

(2) 現(xiàn)行熱學(xué)教材中有關(guān)克勞修斯等式的證明確實(shí)存在文字論證過于簡單、不夠嚴(yán)謹(jǐn)?shù)膯栴}.有些用語，例如“當(dāng)小卡諾循環(huán)的數(shù)目趨向無窮大時(shí)，鋸齒形曲線就趨向原可逆循環(huán)……”表述上存在歧義.產(chǎn)生歧義的主要原因來自于對卡諾循環(huán)分解與原循環(huán)“等效性”的理解上.這里“鋸齒形曲線就趨向原可逆循環(huán)”應(yīng)當(dāng)理解為：當(dāng)n→∞時(shí)，由n個(gè)卡諾循環(huán)外緣絕熱線與等溫線構(gòu)成的鋸齒循環(huán)曲線上的所有點(diǎn)收斂到l之上；鋸齒循環(huán)曲線所圍面積收斂于原循環(huán)l所圍的面積.

(3) 對于克勞修斯等式證明問題，如果將“等效性”理解為原循環(huán)l上被微小卡諾循絕熱線分割的微元(Pi-1,Pi)上熱溫比的積分值，與沿相應(yīng)的鋸齒形路徑(Pi-1aibiciPi)熱溫比的積分值，在n→∞時(shí)的極限意義下相等，則借助于卡諾循環(huán)分解方法，克勞修斯等式可以從數(shù)學(xué)上加以嚴(yán)格證明.

參考文獻(xiàn)

[1]張錫鈞.任意可逆循環(huán)如何分解為一系列卡諾循環(huán)[J].山東師大學(xué)報(bào)(自然科學(xué)版),1990,5(4):105-107.

[2]賀成緒,張可,談應(yīng)潮,等.在可逆循環(huán)熱溫比之和為零的推導(dǎo)中存在的問題及解決辦法[J].物理與工程, 2005, 15(2):15-17.

[3]李品鈞.關(guān)于克勞修斯等式證明的再討論[J].物理與工程, 2014,24(5):64-65.

[4]李椿,章立源,錢尚武.熱學(xué)[M].北京:高等教育出版社, 2008:169.

[5]秦允豪.熱學(xué)[M].北京:高等教育出版社,2011:271-272.

[6]趙凱華,羅蔚茵.熱學(xué)[M].北京:高等教育出版社,1998: 190-192.

[7]馬春曦,朱元海,桑希勤.克勞修斯不等式證明的一點(diǎn)補(bǔ)充[J].大慶石油學(xué)院學(xué)報(bào),2006,30(5):93-95.

[8]張三慧.大學(xué)物理學(xué)：第二冊,熱學(xué)[M].北京:清華大學(xué)出版社,1999:187-195.

[9]陳守洙,江之永.普通物理學(xué)[M].北京:高等教育出版社, 1998:376-377.

[10]馬文蔚,物理學(xué)[M].北京:高等教育出版社,2000:211-213

[11]李椿,章立源,錢尚武.熱學(xué)[M].北京:人民教育出版社，1978:257.

■

作者簡介:蔣小勤, 男, 教授，主要從事物理教學(xué)科研工作，研究方向?yàn)榱黧w物理學(xué). xqjiang888@qq.com

收稿日期:2015-01-05