織機經紗張力自適應滑模控制器的設計與仿真*
孫 哲,吳震宇,武傳宇,金英子
(浙江理工大學機械與自動控制學院,浙江杭州310018)
0 引 言
織機送經機構除了要按織造需求適時送出相應長度的經紗外,還要使經紗保持一定的張力,因為經紗張力會直接影響到紡織品的產量和質量。如果經紗承受的張力平穩,可以有效抑制開車痕等現象。經紗張力的控制性能將會影響經紗張力的波動,從而影響織機的車速和效率,并最終影響織物的質量[1]。因此,合理的經紗張力控制方法對于提高織機生產效率和紡織品質量具有重大意義。
近年來,越來越多智能化、自動化的控制方法開始走進人們的視野,被應用于織機送經機構以維持經紗張力的恒定。劉官正[2]提出了一種基于Kalman 濾波器的RBF 神經網絡整定PID 控制,在經紗張力控制上取得了良好的控制效果。林坤[3]將單神經元自適應控制應用于織機送經系統,具有良好的跟隨特性,能有效改善系統的動態性能。張榮臻[4]將模糊專家控制和模糊神經網絡控制應用于織機送經卷取機構中經紗張力的控制,保證了控制系統的控制精度和魯棒性。
目前織機經紗張力控制方法中比較普遍的有PID控制、模糊PID 控制和神經網絡控制等,而自適應滑模控制[5]方法在織機上的應用很少。
本研究將針對織機送經卷取系統設計一種自適應滑模控制器,并對其進行研究和分析。
1 被控對象動力學模型的建立
織機的結構簡圖如圖1 所示,主要包括開口機構、引緯機構、打緯機構、送經機構和卷取機構等。綜框在開口機構的作用下將經紗提起或下拉,形成一個菱形的梭口,讓緯紗通過梭口后,綜框回位使梭口閉合,讓經紗夾持住緯紗。隨后,緯紗在鋼筘的前向擺動作用下被打向織口。同時,卷取機構將織物卷入落布輥,送經機構驅動織軸轉動送出一定量的經紗,從而維持經紗張力恒定。
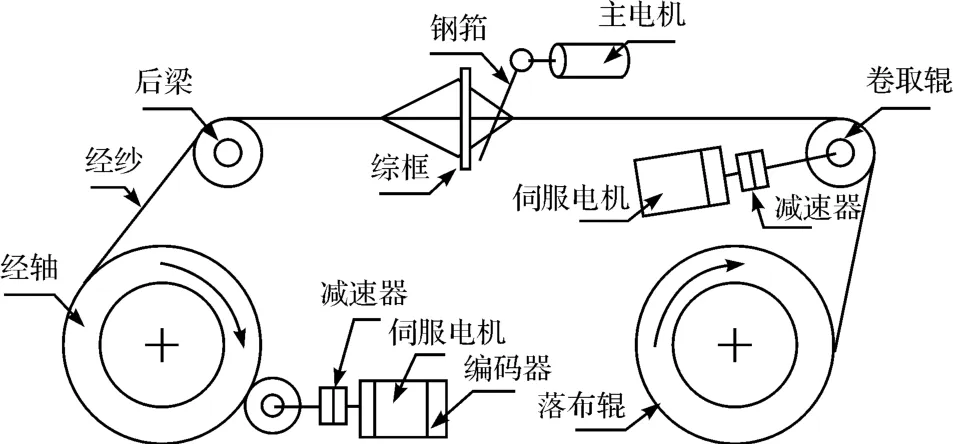
圖1 織機結構
織機中的卷取輥一般是恒速轉動的,所以,為了維持經紗張力恒定,系統主要的控制對象是驅動經軸轉動的伺服電機,通過控制其轉矩而控制經軸轉動速度,從而控制經軸送經量,以維持經紗張力恒定。因為綜框大約是以5 Hz 的頻率在開口機構的帶動下進行啟閉運動,這個啟閉運動是周期性的,加之開口運動對經紗張力改變的模型十分復雜,本研究可以近似地用一個頻率為5 Hz 的正弦信號來模擬綜框啟閉運動對經紗張力的影響,即系統的外界干擾。
后梁上安裝有經紗張力傳感器,檢測到的經紗張力即系統輸出;而除去外界干擾下的線性系統被控對象的傳遞函數的表達式為[6-7]:
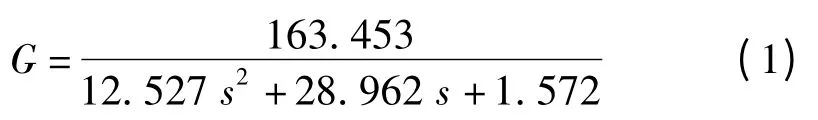
2 自適應滑模控制器的設計
自適應滑模控制系統結構圖如圖2 所示。
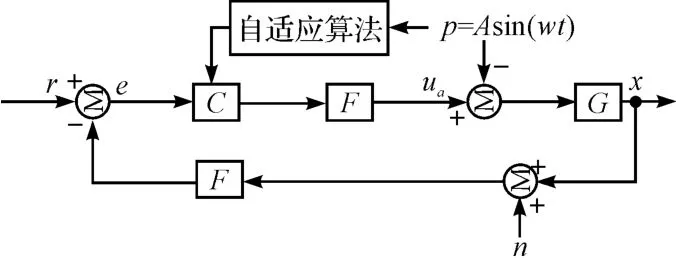
圖2 自適應滑模控制系統結構圖
在圖2 中,其傳遞函數為:
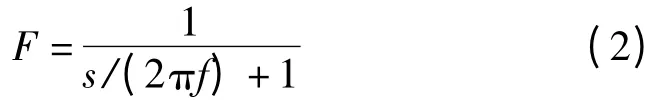
式中:f—截止頻率。
為了方便設計自適應滑模控制器,筆者用字母表示傳遞函數G:
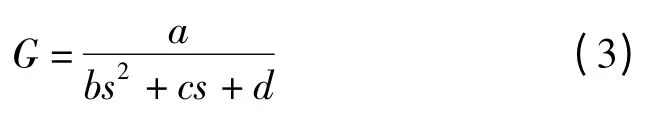
因為參數a 體現的是對控制器輸出信號u 的放大程度,而送經電機減速器的傳動比等參數相對精確,可以認為a 是精確的。
給出參數b,c 和d 的上限:

定義跟蹤誤差e 為:

定義滑動變量S 為:

式中:λ >0。
設計出自適應滑模控制器輸出信號為:
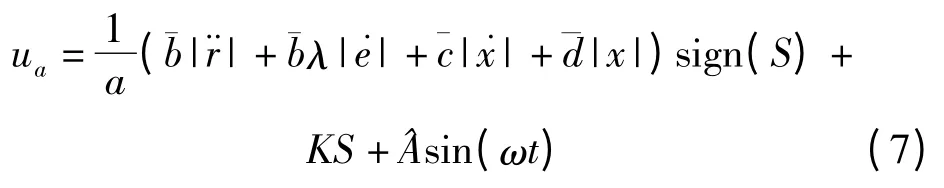
式中:K >0;sign(S)—關于滑動變量S 的符號函數;的估計值,其包含的自適應算法如下:

式中:ρ—自適應增益[8],ρ >0,它的選取將會影響到自適應算法對參數A 估計的速率及準確度,進而影響到能否快速有效地補償外界干擾。
針對同一個被控對象模型,本研究用一個PID 控制器[9]和一個滑模控制器與所設計的自適應滑模控制器進行比較。
PID 控制器輸出信號uP如下[10]:
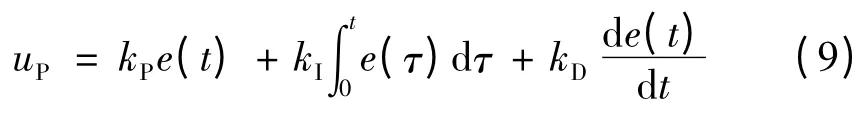
式中:跟蹤誤差e 的定義同式(4);kP,kI,kD—比例增益、積分增益和微分增益。
給滑模控制器輸出信號也引入低通濾波器F,并將滑模控制器輸出信號設計為:
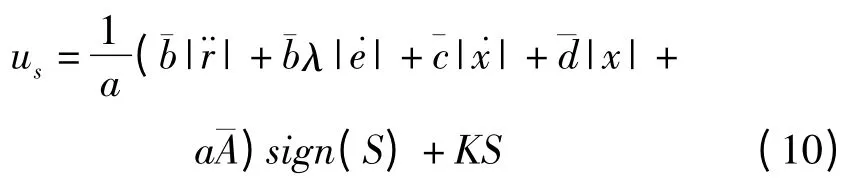

3 系統穩定性證明與仿真結果分析
為了證明自適應滑模控制系統的穩定性,定義李雅普諾夫函數V 為:
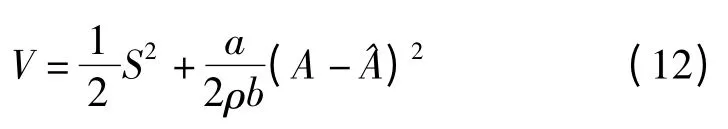
經過式(13)的推導,得到李雅普諾夫函數V 的一階導˙V≤0,證明了控制系統的穩定。本研究經過不斷地調試,對3 種控制器的控制參數賦值如下:
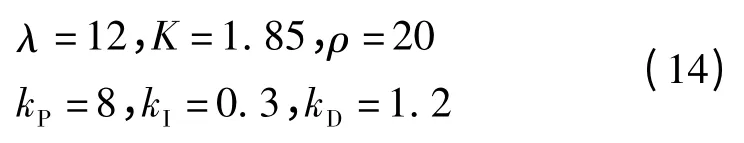
給定經紗張力值r 為:

噪聲n 采用一個均值為0.000 01 N、方差為0.00 01 N2的隨機噪聲信號。濾波器F 的截止頻率f 被設置為10 Hz。為了進一步減小抖振,本研究采用飽和函數sat(S)來替代式(7)和式(10)中的符號函數sign(S)[11],飽和函數的表達式如下:
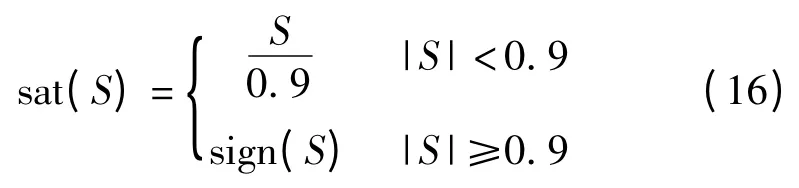
本研究運用Simulink 對這3 種控制器進行仿真,采用固定步長的設置和歐拉-1 型的仿真運算解法,將采樣周期設置為:

得到的仿真對比結果如圖(3~5)所示。
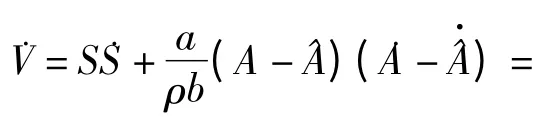
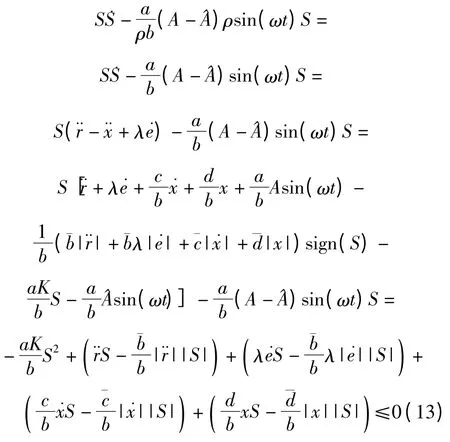
瞬態響應下3 種控制器控制性能的對比結果如圖3 所示。結果顯示,PID 控制器的上升時間最短,但是進入穩態的時間最長,約為0.6 s,且存在較大超調。滑模和自適應滑模控制器的上升時間稍長,但是幾乎沒有超調,進入穩態的時間也較短,僅為0.4 s 左右,意味著跟蹤誤差可以更快地收斂到一個有界區域內。
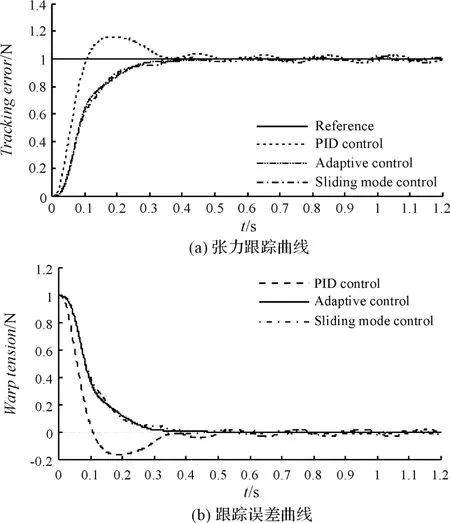
圖3 瞬態響應下3 種控制器性能比較
穩態下3 種控制器控制性能的對比結果如圖4 所示。因為外界干擾p 的存在,3 種控制器作用下的系統輸出信號都會圍繞參考信號上、下波動,但波動幅度有所不同。PID 控制器的穩態誤差最大,其峰值約為0.028 N;其次是滑模控制器,誤差峰值為0.019 N 左右;自適應滑模控制器的穩態誤差最小,其峰值在0.01 N以下。
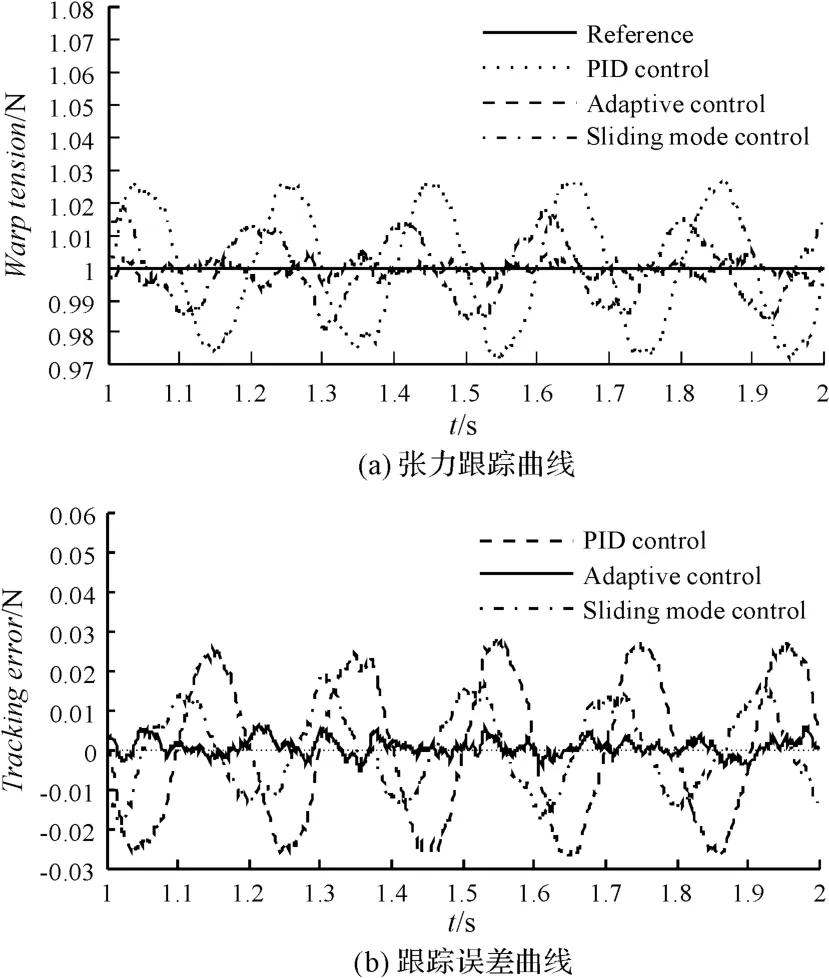
圖4 穩態下3 種控制器性能比較
控制器輸出信號如圖5 所示。
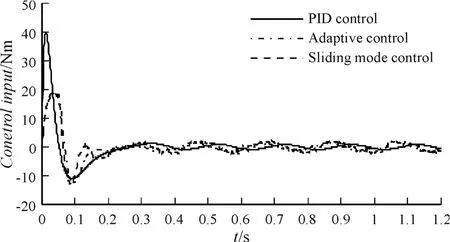
圖5 控制器輸出信號曲線
圖5 顯示,在響應開始時PID 控制器的控制量約為40 N·m,而滑模和自適應滑模控制器的控制量峰值約為20 N·m。雖經濾波,滑模類控制器輸出信號的抖振仍比PID 控制器稍大,這歸因于它們較強的非連續性,但是抖振對控制性能的影響基本可以忽略。可見,自適應滑模控制不僅可以保證控制系統的魯棒性,而且可以通過自適應算法學習出系統的外界干擾并進行有效地補償,其控制性能優于PID 控制和傳統滑模控制。
4 結束語
筆者研究了經紗張力控制的被控對象和控制方法,考慮到被控模型的非線性特性,采用了正弦信號來模擬系統外界干擾,設計了一種自適應滑模控制器,運用李雅普諾夫判據證明了控制系統的穩定,并運用低通濾波器過濾了系統輸出信號中的高頻噪聲。
本研究對自適應滑模控制器和一個PID 控制器、一個傳統滑模控制器進行了仿真對比,結果表明,所設計的自適應滑模控制器具有響應快、無超調、穩態誤差小、魯棒性強等優點,具有廣闊的應用前景。
[1]陳家新,施廣軍,楊立新. 劍桿織機經紗張力數學模型及仿真[J].東華大學學報,2012,38(4):465-470.
[2]劉官正.織機經紗張力控制策略研究[D]. 杭州:浙江大學電氣工程學院,2008.
[3]林 坤.基于自適應算法的電子送經卷取控制系統設計[D].杭州:浙江理工大學機械與自動控制學院,2010.
[4]張榮臻.織機經紗張力智能控制策略研究[D]. 杭州:浙江大學電氣工程學院,2010.
[5]劉金琨.滑模變結構控制Matlab 仿真[M].北京:清華大學出版社,2012.
[6]周其洪.新型高速織機的關鍵控制技術研究[D]. 上海:上海大學機電工程與自動化學院,2008.
[7]劉衛東,常安濤,劉和進,等.基于AT9261 和CAN 總線的高檔織機控制器上位機系統設計[J].輕工機械,2013,31(5):41-44.
[8]TAN K K,HUANG S N,JIANG X. Friction modeling and adaptive compensation using a relay feedback approach[J].IEEE Transactions on Industrial Electronics,2001,48(1):169-176.
[9]薛定宇.控制系統計算機輔助設計[M].北京:清華大學出版社,2006.
[10]王衍平.單神經元PID 算法在包裝機溫控系統中的應用[J].包裝與食品機械,2013(3):69-72.
[11]UTKIN V. Sliding mode control in electro-mechanical systems[M].New York:Taylor & Francis,2009.

