基于馬爾可夫模型的風力發電系統可靠性分析

秦 洋，馬慧民 ，陳玉晶

(上海電機學院電氣學院，上海200240)

0 引 言

近年來，世界風電產業迅速發展，已成為可再生能源發電行業中不可或缺的重要力量，正朝著大容量、高質量的海上風電方向發展。隨著裝機容量的不斷提高，風電機組的結構也越來越復雜，伴隨著機組運行環境的惡劣，致使風電機組的故障率居高不下，風力發電系統作為風機最為關鍵的系統，其性能直接影響到機組運行的可靠性和穩定性，因此，在追求發電容量的同時，必須考慮其可靠性［1］。

目前，國內外學者研究工作主要集中于風電機組的狀態監測與故障診斷上［2-5］，大多是通過神經網絡、支持向量機、小波分析等診斷方法，結合機組的運行狀態，建立相應的風機故障診斷或狀態評估模型，理論上較為成熟，而對風機可靠性及運行維護策略研究尚處于起步階段，國內外都鮮見報道。

馬爾可夫過程是一種基于概率統計的特殊隨機過程，是可靠性工程中極為重要的理論工具，它對系統的可靠性分析已被用于多個領域，但研究對象主要集中于單部件、多部件的串聯、并聯及冗余系統等［6-7］。

筆者在研究風力發電系統關鍵部件故障機制的基礎上，考慮到系統中部件之間的運行是不完全獨立的情況，把馬爾可夫過程理論應用到風機發電機-變流器系統可靠性分析中，建立基于有向網絡的馬爾可夫過程［8］的風機發電系統可靠性模型，為科學制定發電系統維護策略提供理論支持。

1 發電系統故障機制分析

風力發電機組通常安裝在偏遠的郊外，在運行過程中內部疲勞累積與外部環境等多種因素相互作用，致使風機關鍵部件的故障率高居不下，根據瑞典風場2000年～2004年間故障數據的統計表明［9］，發電系統是機組中最常發生故障的系統，也是引起風機停機時間的主要原因，其故障率高達23%，其中故障最為頻繁的是發電機和變流器故障。

現國內采用最多的是雙饋異步風力發電機，其原理如圖1 所示。

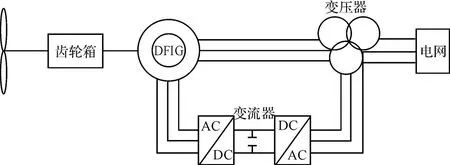
圖1 雙饋異步風力發電機原理圖

風機運行工況復雜、電網負荷持續變化，易使發電機溫度過高、振動過大而損壞發電機的軸承及繞組的絕緣性能，因此雙饋異步發電機的故障率明顯高于其他發電機，據統計異步發電機中最常發生故障的部位是軸承、定子、轉子，三者的故障率分別為40%、38%、10%［10］。

變流器是發電系統中實施能量轉換的關鍵部件，其采用變速恒頻技術，把風力機發出的電能轉換為電壓和頻率都穩定的電能送入電網。變流器工作環境惡劣，高溫發熱、電磁干擾、油液腐蝕等都極易影響變流器的性能而導致變流器發生故障，且故障主要發生在控制驅動單元、直流母線環節、逆變器等組件中［11］，這些組件均是由各類電力電子器件構成的，其中使用較多的是絕緣柵雙極晶體管，當其兩端過壓、過流時都可能使晶體管超過耐受溫度而擊穿或燒毀，造成風機變流器發生故障。

2 發電系統可靠性建模

2．1 馬爾可夫過程

馬爾可夫過程［12］是一種基于概率統計的隨機過程，它能夠描述系統在投入運行后狀態之間相互轉移的過程，該過程具備無后效性。通常只要系統中某個狀態一經決定，則系統下一個狀態的概率即可確定，并且與系統之前的狀態無關，是對可修復系統進行可靠性分析的有力工具。

應用馬爾可夫過程建立風電發電機-變流器系統的可靠性分析模型，需要作出如下假設:

(1)系統中部件只有正常和故障2 種狀態，并且狀態可以相互轉換;

(2)系統中部件處于正常或故障狀態是相互獨立的;

(3)系統中部件失效分布和維修分布均服從指數分布，即各部件的故障率和修復率均為常數;

(4)系統投入運行時是新的且處于工作狀態，發生故障后立刻進入維修狀態。

2．2 部件的可靠性模型

發電系統的故障主要分為電氣故障和機械故障，筆者研究主要針對電氣故障。依據風機發電系統故障機制分析，發電機故障主要包括定子繞組故障、轉子繞組故障、軸承故障，變流器故障主要包括機側及網側變換器故障、控制單元故障、直流環節故障等，這些組件的可靠性參數如表1 所示。

表1 發電機、變流器可靠性參數

在這些相互獨立的組件中，任意組件發生故障都將影響到發電機、變流器的正常工作，因此，可以把這些組件看成串聯系統，根據串聯系統的可靠性分析，發電機子系統1 和變流器的子系統2 的可靠性模型為:

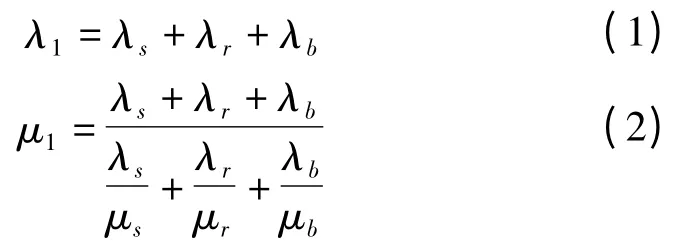
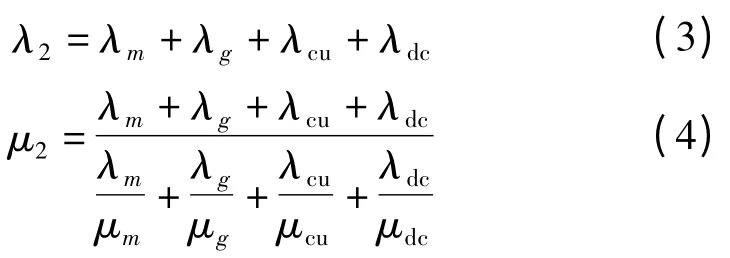
2．3 發電系統的可靠性模型

雙饋異步風力發電機［13］的變流器和發電機的連接方式不是簡單的串聯關系，感應電動機的定子端直接接入電網，而轉子端通過變流器接入電網，只有20%～30%的功率通過變流器經穩壓后傳入電網，所以發電機子系統1 和變流器子系統2 不再是串聯系統，需要通過運用馬爾可夫過程對系統進行可靠性建模。

從發電系統的運行狀態可以看出，系統的狀態集S={0，1，2，3}，系統正常狀態集W={0}，系統的故障狀態集F={1，2，3}，由于分布為指數分布，隨機過程{~X(t)，t≥0}為有限齊次馬爾可夫鏈。

根據發電系統的模型，得出系統在Δt 時間內狀態轉移圖，如圖2 所示:

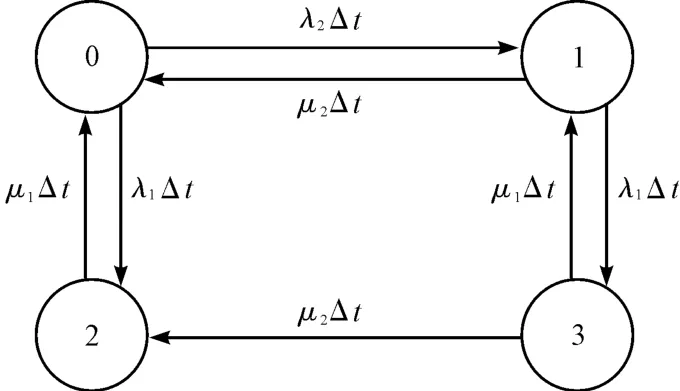
圖2 馬爾可夫發電系統狀態轉移圖

根據圖2 得到轉移概率矩陣為:

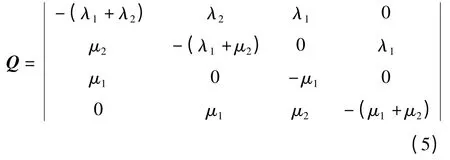
2．3．1 系統的瞬時可用度

系統的瞬時可用度是在t 時刻發電機、變流器都處于正常工作狀態的概率為:

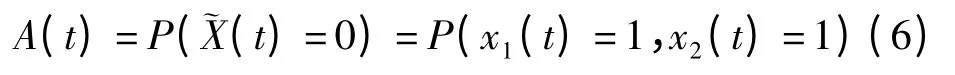
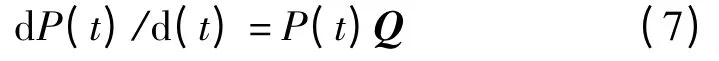
對該式作拉普拉氏變換、再進行拉普拉氏逆變換，得到系統的可用度為:

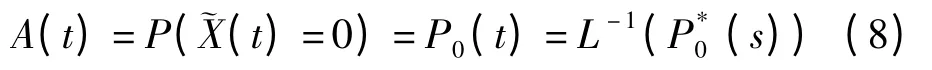
2．3．2 系統可靠性的穩態指標

根據式(5)的狀態轉移矩陣Q，可得到系統的可靠性的穩態指標和平均指標，令系統的穩態概率值分別為π0、π1、π2、π3，得到系統穩態方程組:

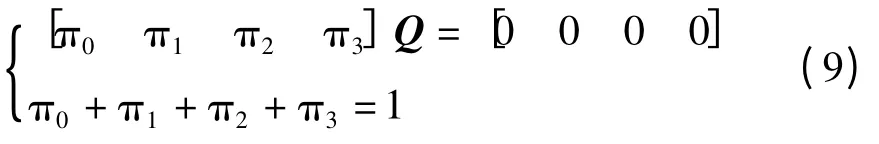
可將矩陣Q 的表達式帶入式(9)，即可求得系統各狀態的穩態概率。系統的穩態可用度、系統的穩態故障頻度、系統平均工作時間、系統平均維修時間分別為:

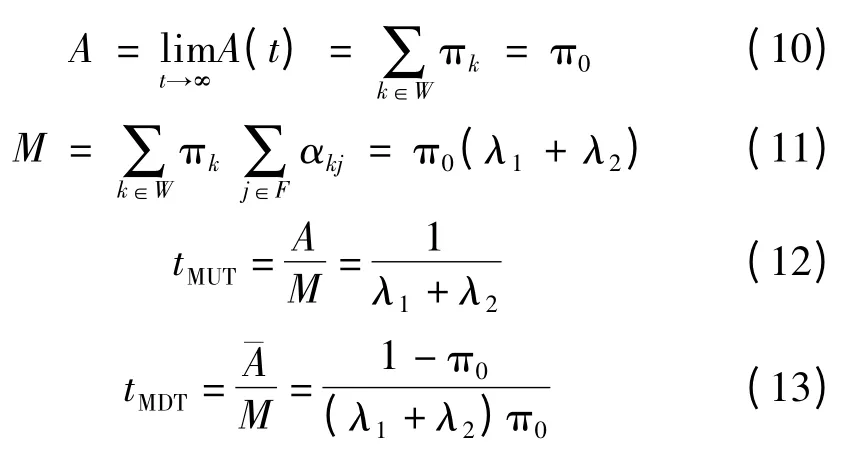
3 實例計算及影響因素分析

3．1 原始數據及計算結果

由于風電機組歷史故障數據資料還比較少，這使得風力發電系統的可靠性參數很難準確獲得，鑒于此，本研究參考有關文獻的可靠性參數對風力發電系統進行可靠性分析［14］。

發電機、變流器各組件的故障率和修復率如表2所示。

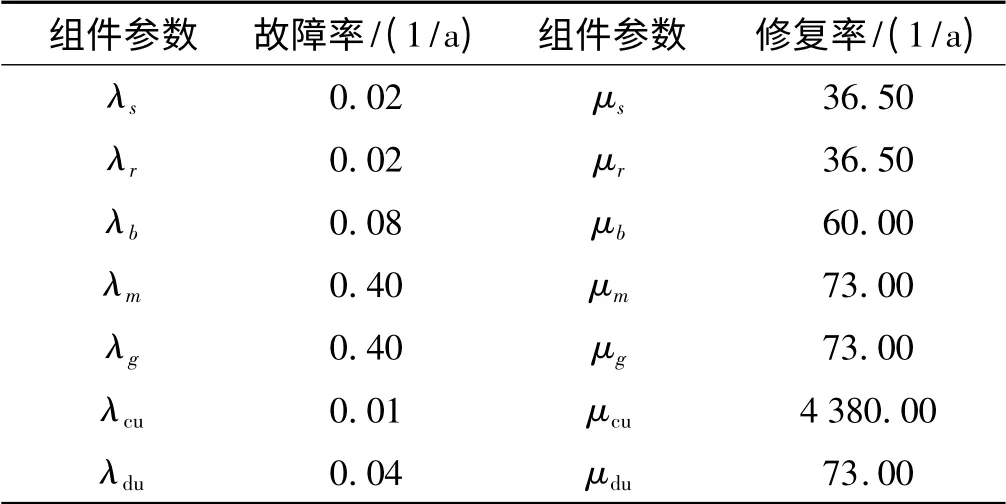
表2 發電機、變流器各組件的故障率和修復率

由表2 可靠性數據，根據式(1～4)計算子系統的模型參數，可得到發電機和變流器的子系統的可靠性參數。

子系統的故障率和修復率如表3 所示。

表3 子系統的故障率和修復率

根據上述表格中可靠性數據，利用Matlab 編程軟件進行編程分析可得到系統的瞬時可用度。

發電系統和子系統的瞬時可用度對比圖如圖3所示。

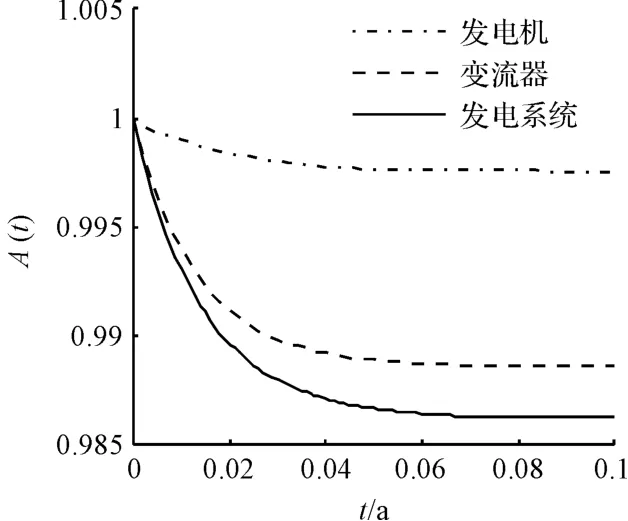
圖3 發電系統和子系統的瞬時可用度對比圖

從圖3 可以看出，如果僅從單部件考慮，發電機子系統、變流器子系統的穩態可用度分別為0． 998、0．989，而整個系統的穩態可用度為0．986，顯然整個系統的穩態可用度要小于單部件的穩態可用度，且系統到達穩態的時間要大于其發電機、變流器子系統到達穩態的時間，驗證了該模型的有效性。整個系統中發電機的運行狀態是獨立，它的可用度與單部件可用度相同，而變流器的運行狀態則要受到系統發電機的影響，因而它的可用度與系統的可用度保持一致。

根據上述公式，筆者計算得到發電系統的穩態可靠性參數，如表4 所示。

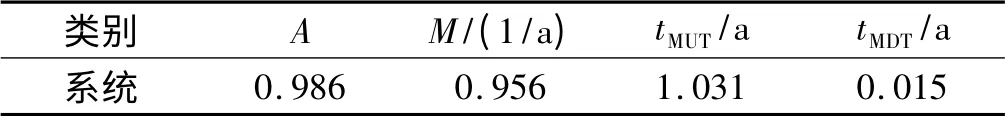
表4 發電系統的穩態可靠性參數

3．2 相關因素分析

風力發電系統上升到穩態所需要的時間與系統部件的故障率及修復率有關系，而系統部件的故障率與部件自身的性能及運行環境有關，因此，本研究探討發電機、變流器的修復率分別取不同數值時，對系統穩態可用度及到達穩態所需時間的影響［15］。

從圖4 與圖5 可以看出，系統達到穩態的時間t與部件的修復率μ 密切相關，系統到達穩態所需要的時間隨μ 的增大而減少，因此，提高部件的修復率是使發電系統盡快到達穩態的有效途徑，并且可以提高系統的穩態可用度。

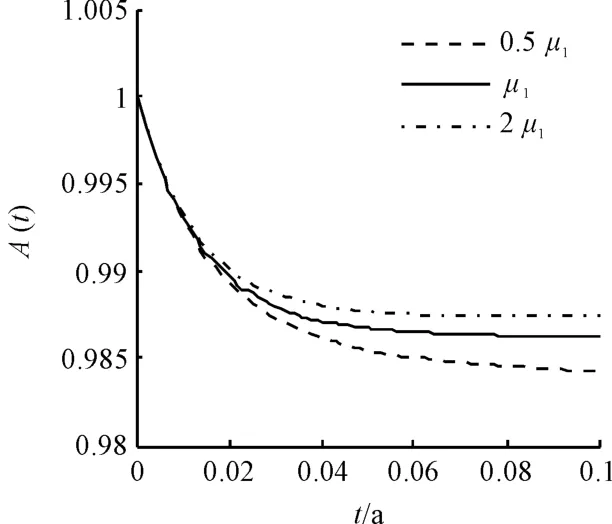
圖4 發電機的修復率與系統可用度的關系

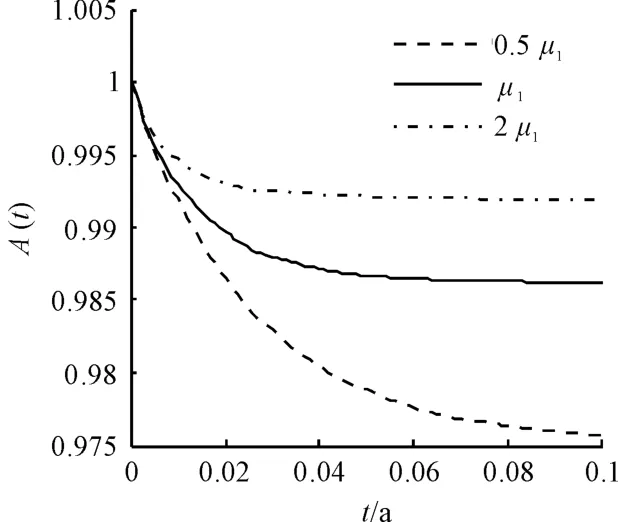
圖5 變流器的修復率與系統可用度的關系

與系統的瞬時可用度相比，工程技術人員往往更加關注系統的穩態可用度［16］，它是系統可靠性評估的重要數據，通過對系統可用度的分析，可以采用最有效、經濟的方式保證設備隨時處于工作狀態，使其充分發揮系統的性能。

發電系統穩態可用度隨部件的故障率與修復率的變化規律如圖6、圖7 所示。

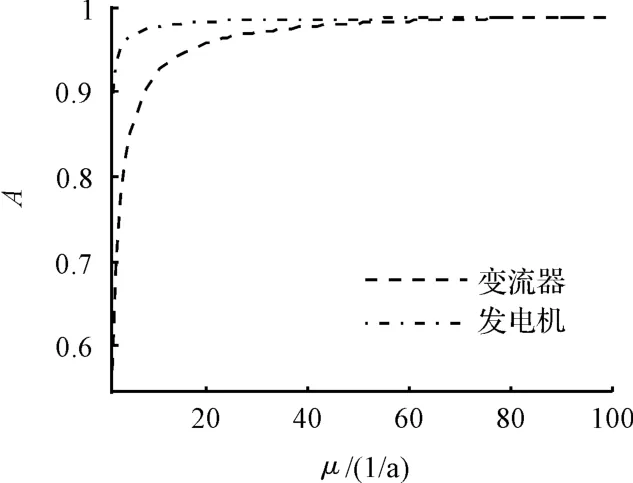
圖6 系統穩態可用度與部件修復率的關系

從圖6 可以看出，發電系統的穩態可用度與發電機、變流器的修復率均密切相關，發電系統的穩態可用度隨部件的修復率增大而提高，當部件的修復率達到30 次以后，系統的穩態可用度上升的比較緩慢，所以單純地提高部件的修復率對提高整個發電系統的可用度效果并不明顯。從圖7 可知，整個發電系統的穩態可用度隨部件的故障率減少而緩慢上升，但上升到一定數值時，系統的可用度將達到定值，即要想提高發電系統的可用度不能僅僅只重視部件的故障率或修復率的大小，而應將兩者綜合起來進行考慮。

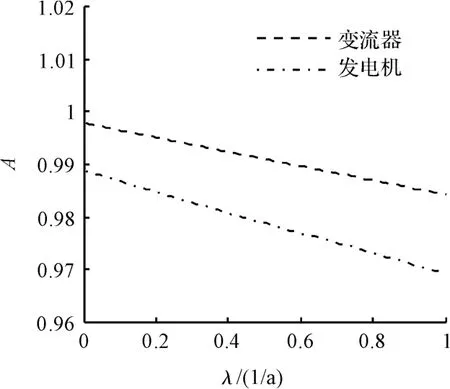
圖7 系統穩態可用度與部件故障率的關系

4 結束語

筆者研究了雙饋異步風力發電系統關鍵部件的故障機制，建立了有向網絡的馬爾可夫可修模型，利用狀態空間法對發電機-變流器系統進行可靠性分析，將復雜的結果用清晰明了的圖形進行分析，達到了很好的效果。分析表明，發電系統的可用度由故障率、修復率共同決定，修復率對系統達到穩態所需時間的貢獻度較大，對開展風機的可靠性研究和評估具有一定的參考價值，同時也為研究多階段有向網絡系統提供了鋪墊作用。

風電機組是集機械、電氣多部件的復雜系統，故障模式及運行狀態復雜多樣，考慮多種失效因子的影響，利用馬爾可夫過程建立涵蓋整個機組綜合狀態的可靠性模型，還有待進一步研究。

［1］TAVNER P J，XIANG J，SPINATO F． Reliability analysis for windturbines［J］．Wind Energy，2007，10(1):1-18．

［2］孟恩隆，郭東杰，王靈梅，等．風力發電機組狀態監測與智能故障診斷系統的設計與實現［J］． 華東電力，2012，40(3):507-510．

［3］梁偉宸，許湘蓮，龐 可，等．風電機組故障診斷實現方法探討［J］．高壓電器，2011，47(8):57-62．

［4］王占霞，張曉波． 基于SOM 網的風電變流器故障診斷［J］．電網與清潔能源，2011，27(4):35-38．

［5］安學利，趙明浩，蔣東翔，等．基于支持向量機和多源信息的直驅風力發電機組故障診斷［J］． 電網技術，2011，35(4):117-122．

［6］吳志良，郭 晨，趙 紅．基于馬爾柯夫過程的可修系統可靠性建模［J］．大連海事大學學報，2007，33(1):13-16．

［7］王賢林，張 華．基于馬爾可夫過程的機電設備有效性模型［J］．機電工程，2008，25(6):5-7．

［8］于明麗，崔利榮．兩階段有向網絡馬爾可夫系統維修模型與分析［J］．北京理工大學學報，2011，31(6):753-756．

［9］RIBRANT J，BERTLING LM，Survey of failures in wind power systems with focus on Swedish wind power plants during 1997-2005［J］． IEEE Transactions on Energy Conversion，2007，22(1):167-173．

［10］POPA L M，JENSEN B-B，RITCHIE E，et al． Condition monitoring of wind generators［J］． IEEE Industry Applications Society Annual Meeting，2003，3:1839-1846．

［11］YANG S，BRYANT A，MAWBY P，et al． An industry –based survey of reliability in power electronic converters［J］．IEEE Transaction on Industry Applications，2011，47(3):1441-1451．

［12］曹晉華，程 侃．可靠性數學引論［M］．2 版，北京:高等教育出版社，2012．

［13］沙 非，馬成廉，劉 闖，等．變速恒頻風力發電系統及其控制技術研究［J］．電網與清潔能源，2009，25(1):44-47．

［14］ARABIAN H H，ORAEE H，TAVNER P J． Wind turbine productivity considering electrical subassembly reliability［J］．Renewable Energy，2010(35):190-197．

［15］于 敏，何正友，錢清泉． 基于Markov 模型的可維修雙機熱備系統可靠性分析［J］． 計算機工程與設計，2009，30(8):2040-2042．

［16］歐 健，李艾華，徐 斌，等．基于Markov 過程的柴油機監控系統可靠性評估［J］． 機電工程，2011，28(11):1319-1323．