基于非圓信號對陣列干擾下的最佳陣元數研究

禹　芳， 司偉建

(哈爾濱工程大學 信息與通信工程學院， 哈爾濱　150001)

?

基于非圓信號對陣列干擾下的最佳陣元數研究

禹芳， 司偉建

(哈爾濱工程大學 信息與通信工程學院， 哈爾濱150001)

摘要：針對理想情況下， 空間譜估計算法的測向性能隨陣元數目增加而提高， 然而實際工程中存在通道不一致和互耦等干擾， 使陣元數目與測向精度不再成正比問題， 提出一種研究最佳陣元數的方法。 在陣列干擾條件下， 利用非圓信號的偽協方差矩陣不為零特性， 基于空間譜估計算法， 以測角精度和測向成功概率為指標， 分別在均勻線陣和均勻圓陣下研究最佳陣元數目。 通過仿真分析得出， 研究不同陣列形式下的不同目標個數的最佳陣元數目， 對抗干擾至關重要。

關鍵詞：陣列干擾; 非圓信號; 最佳陣元數; 波達方向估計

0引言

隨著陣列信號處理技術的不斷提高， 如何利用信號的非圓特性進行相關估計已經成為一個熱點話題。 非圓信號這一概念也已被拓展至信號檢測、 濾波、 參數估計等各個領域。 利用信號的非圓特性來提高波達方向估計的性能， 成為了研究的熱點[1-3]。

由于非圓信號的偽協方差(也叫做橢圓協方差)不為零， 即陣列輸出信號的偽協方差矩陣不為零， 可以多增加利用這一維信息， 提高子空間算法的性能， 可測信源數也加倍[4]。 目前， 常見的非圓信號有幅度調制(amplitude modulation， AM)、 二進制相移鍵控(binary phase shift keying， BPSK)和多進制幅度鍵控(multiple amplitude shifting keying， MASK)等[5]。 這些非圓信號被廣泛的應用于雷達、 衛星通信和現代通信系統領域。 在實際工程中， 常會有各種干擾(陣元方向圖不同、 陣元通道幅相不一致、 陣元位置及陣元間互耦)[6-8]的存在， 陣列流型會有偏差或者擾動， 就會影響空間譜估計各種算法[9-10]的測向性能， 從而直接導致對目標源的測向精度和分辨力急劇下降[11]。 所以， 干擾的存在是空間譜估計亟需解決的難點之一， 使用最佳的陣元數可有效避免這一點。

本文先建立通道不一致與互耦干擾的數學模型， 然后提出基于非圓信號的多重信號分類算法(MUSIC algorithm for noncircular signals， NC-MUSIC)， 最后在存在陣列干擾的條件下， 利用NC-MUSIC算法分析陣列形式為均勻線陣與均勻圓陣時， 給出最佳的陣元個數。

1數學模型

設有q個遠場窄帶非圓信號入射到天線陣列上， 陣元數為M， 天線模型如圖1~2所示。

天線陣列接收的數據矩陣為

X(t)=A(α, β)S(t)+N(t)

(1)

式中： (α,β)分別為信號入射的方位角和俯仰角，A(α,β)=[a(α1,β1),…,a(αq,βq)]為M×q維的導向矢量矩陣；S(t)=[s1(t),…,sq(t)]為q×1維的信號矢量矩陣；N(t)=[n1(t),…,nM(t)]為M×1維的零均值加性復圓高斯白噪聲矩陣。

假設信號源之間互不相關， 則偽協方差矩陣有

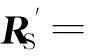
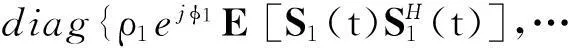
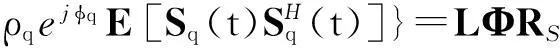
(2)

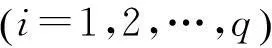
2陣列干擾模型

2.1　通道不一致

通道不一致主要指的是相位不一致， 即在每個陣元通道中加入不同的附加相位。 通道不一致一般是對陣列流型產生擾動， 具體模型如下所示：

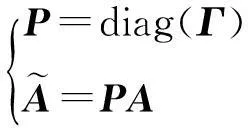
(3)

2.2　互耦

當天線工作的頻率比較高時， 為了避免測向模糊問題， 陣元間的間距要小于等于波長的一半， 這樣使兩陣元之間的間距比較近， 陣元之間的互耦效應會明顯加強。 具體模型如下所示：

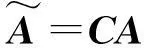
(4)

式中： C為陣元之間的互耦矩陣。

假設自由度為3， 均勻線陣和均勻圓陣的互耦系數矩陣分別為

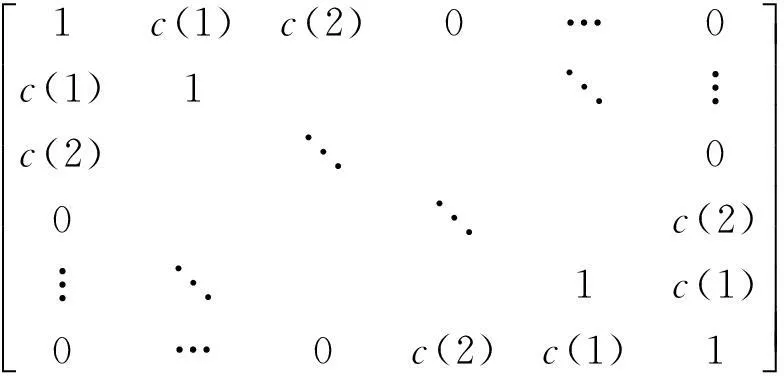
(5)

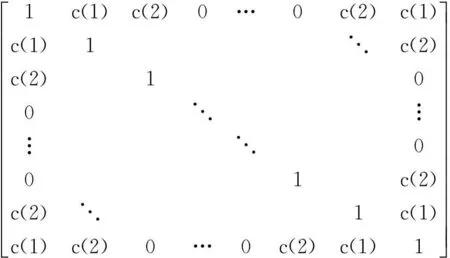
(6)

3基于非圓信號的干擾MUSIC算法

構造的擴展陣列數據矩陣為

(7)

假設信號源與噪聲源之間是相互獨立的， 則擴展的陣列數據矩陣的協方差矩陣為

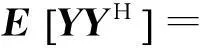
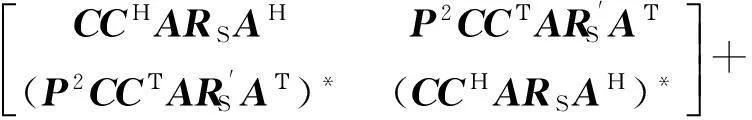
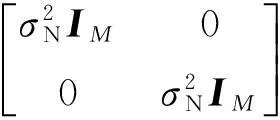
(8)

將上式改寫成如下形式：

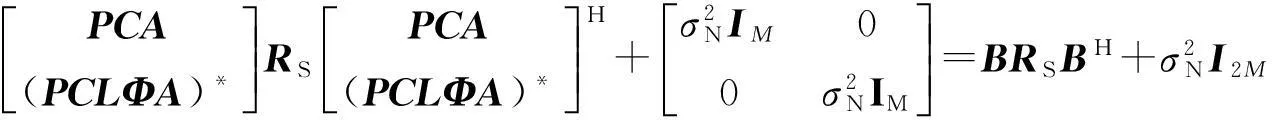
(9)

接下來， 對擴展的協方差矩陣進行特征分解， 可以得到下面的形式：

(10)

其中， 將特征值按由大到小的順序排序， 大特征值∑S=diag(λ1,λ2,…,λq)對應的信號子空間為US=[U1,U2,…,Uq]； 小特征值∑N=diag(λq+1,λq+2,…,λM)對應的噪聲子空間為UN=[Uq+1,Uq+2,…,UM]。

導向矢量與噪聲子空間是正交的， 即

BΗUN=0

(11)

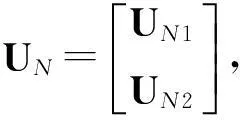
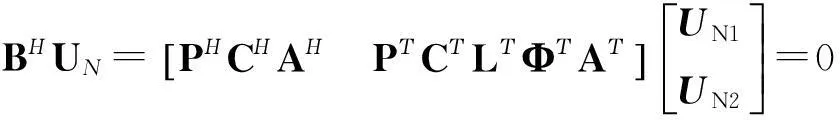
(12)

將式(12)展開成如下形式：

PHCHAHUN1+PΤCΤLΤΦΤAΤUN2=0

(13)

把導向矢量矩陣換成搜索的角度導引矢量， 用F范數來求取譜函數， 即

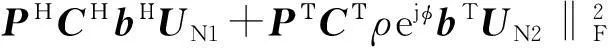
(14)

UN1與UN2存在如下關系[12]：

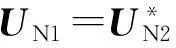
(15)

根據式(15)， 可以推導以下關系式：

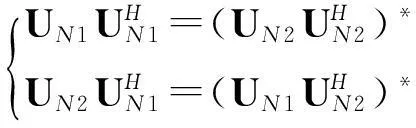
(16)

譜函數可根據式(14)化簡， 得

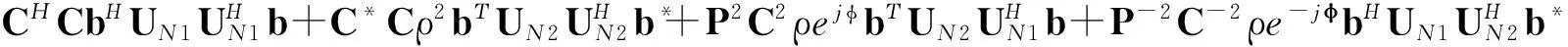
(17)

對式(17)求φ的偏導，并令其為零，可得到如下關系：

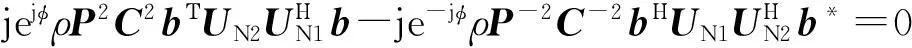
(18)

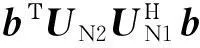
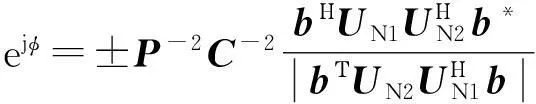
(19)

為使譜函數為最小值， 取ejφ的負值， 將其代入式(17)， 可得

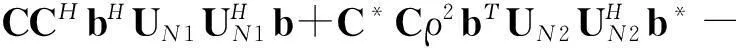
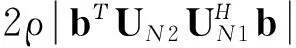
(20)

假設入射信號為最大非圓率信號， 則式(20)可寫成

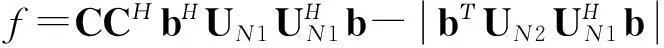
(21)

根據上面的譜函數， 可以估計來波方向。 特征分解得到的噪聲子空間有一定的誤差，導致式(21)不再是零向量， 而是趨近于零， 所以求式(21)的倒數， 找極大值。 根據搜索矢量， 角度的不斷變化， 極大值對應的位置即為來波方向。

4仿真分析

實驗條件： 信號頻率為8 GHz， 信噪比為20 dB,快拍數為100， 噪聲為零均值的復圓高斯白噪聲， 角度搜索步長為0.5°， 每次仿真進行100次Monte-Carlo實驗。

成功測向概率定義為正確測向的次數與實驗次數的比值， 其中估計的值與真實值的絕對值小于2°。

定義測角精度均方根誤差RMSE和成功測向概率η為

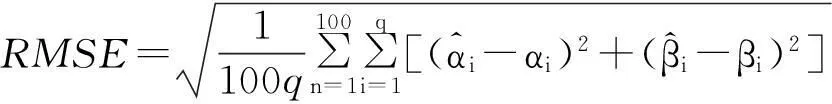
(22)

(23)

式中： h為成功測向次數。

4.1　NC-MUSIC算法與MUSIC算法的比較

入射兩個最大非圓率BPSK信號， 非圓相位為10°和20°， 方位角為20°和30°， 陣元間距為入射信號的半波長， 加入的每個通道相位不一致在0°~10°之間， 只考慮相鄰兩個陣元間的互耦效應， 且設兩陣元間的互耦系數為0.255 7+0.192 3j。 分別在陣元數為8和10下用NC-MUSIC算法和MUSIC算法進行仿真， 統計有干擾和無干擾條件下的譜函數如圖3~6所示。

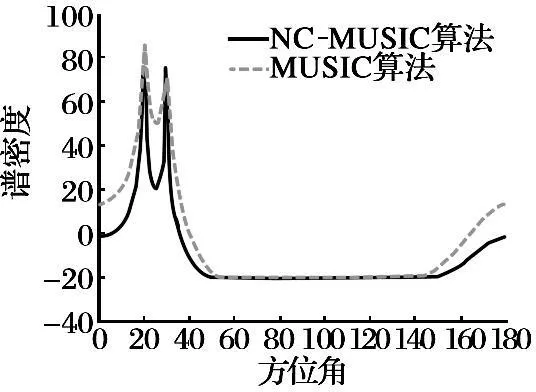
圖3　8陣元不存在干擾時譜峰圖

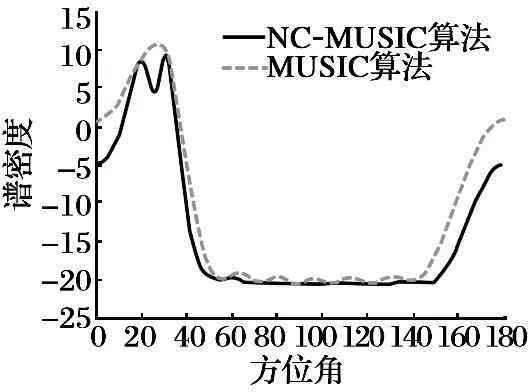
圖4　8陣元存在干擾時譜峰圖

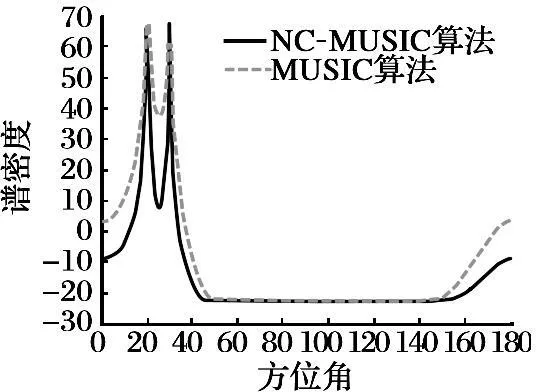
圖5　10陣元不存在干擾時譜峰圖

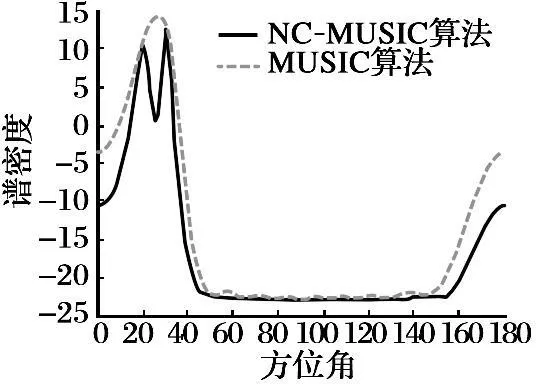
圖6　10陣元存在干擾時譜峰圖

由圖3和圖5的結果可以看出不存在干擾時， NC-MUSIC算法和MUSIC算法都能對來波方向進行估計， 但是NC-MUSIC算法的譜峰圖更尖銳， 估計精度更高； 在加入陣列干擾后， MUSIC算法已經不能正確估計了，對研究最佳陣元數已經沒有意義。 由圖4和圖6可以看出， 隨著陣元數的增加， 雖然MUSIC算法估計精度增加， 但是加入干擾后， 同樣不能正確估計來波方向， 所以NC-MUSIC算法具有更大的優勢。

4.2　均勻線陣

實驗1: 一個信號。入射信號為最大非圓率BPSK信號，非圓相位為10°，入射方位角為20°，陣元間距為入射信號的半波長，加入的每個通道相位不一致在0°~10°之間，只考慮相鄰兩個陣元間的互耦效應，且設兩陣元間的互耦系數為0.255 7+0.192 3j。陣元數在3~10之間變化，在每個陣元下用NC-MUSIC算法進行100次Monte-Carlo實驗，統計不同陣元數的成功測向概率和均方根誤差結果如圖7~8所示。

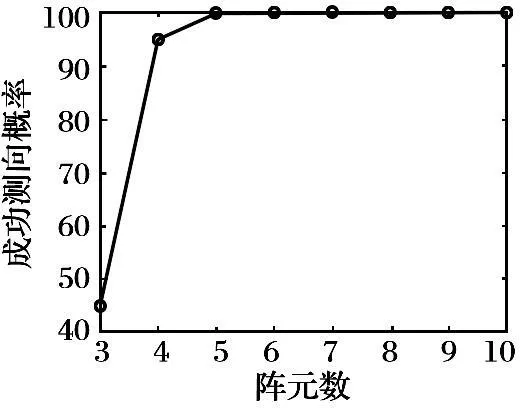
圖7　一個信號時成功測向概率與陣元數的關系曲線

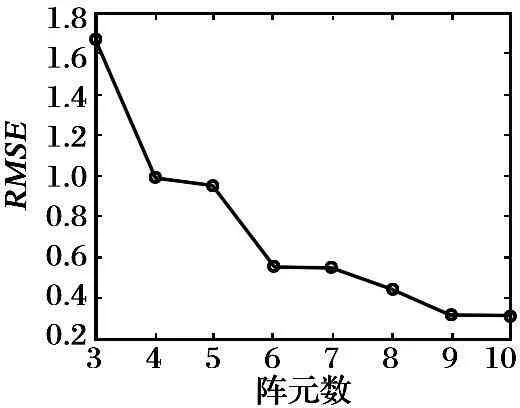
圖8　一個信號時均方根誤差與陣元數的關系曲線

由圖7~8的結果可以得出， 進行單目標測向時， 隨著陣元數的增加， 成功測向概率也隨之增加， 當陣元數為5時， 成功測向概率就能達到100%， 而此時的測向誤差較大； 當陣元數為9和10時， 成功測向概率和測向誤差均一致， 考慮經濟成本， 優先選擇9陣元。

實驗2： 兩個信號。 信號為最大非圓率BPSK信號， 非圓相位為10°和20°， 入射方位角為20°和30°， 陣元間距為入射信號的半波長， 加入的每個通道相位不一致在0°~10°之間， 只考慮相鄰兩個陣元間的互耦效應， 且設兩陣元間的互耦系數為0.255 7+0.192 3j。 陣元數在3~10之間變化， 在每個陣元下用NC-MUSIC算法進行100次Monte-Carlo實驗， 統計不同陣元數的成功測向概率和均方根誤差結果見圖9~10。

由圖9~10的結果可以得出， 進行雙目標測向時， 隨著陣元數的增加， 成功測向概率也隨之增加， 當陣元數為6時， 成功測向概率能達到100%， 而此時的測向誤差較大， 由于干擾的影響， 測向誤差不再隨陣元數增加而降低； 當陣元數為7時， 成功測向概率為100%， 均方根誤差為1°， 所以雙目標進行測向時， 7陣元最優。

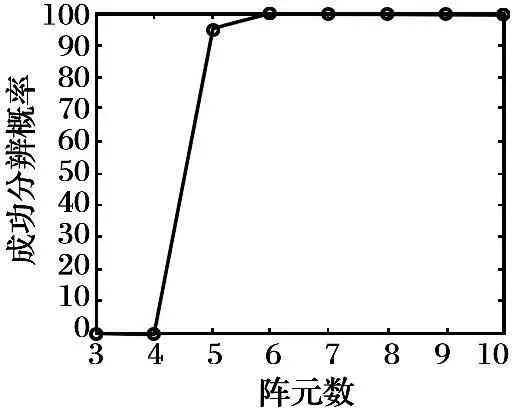
圖9　兩個信號時成功測向概率與陣元數的關系曲線

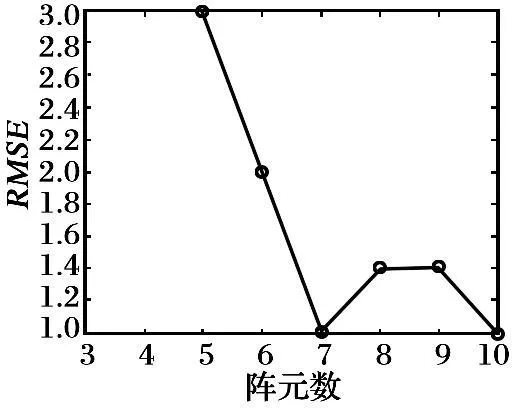
圖10　兩個信號時均方根誤差與陣元數的關系曲線

4.3　均勻圓陣

實驗3： 一個信號。 入射信號為最大非圓率BPSK信號， 非圓相位為10°， 入射方位角為20°， 俯仰角為80°， 均勻圓陣的直徑為300 mm， 加入的每個通道相位不一致在0°~10°之間， 只考慮相鄰兩個陣元間的互耦效應， 且設兩陣元間的互耦系數為0.2557+0.1923j。 陣元數在5~10之間變化， 在每個陣元下用NC-MUSIC算法進行100次Monte-Carlo實驗， 統計不同陣元數的成功測向概率和均方根誤差結果如圖11~12所示。

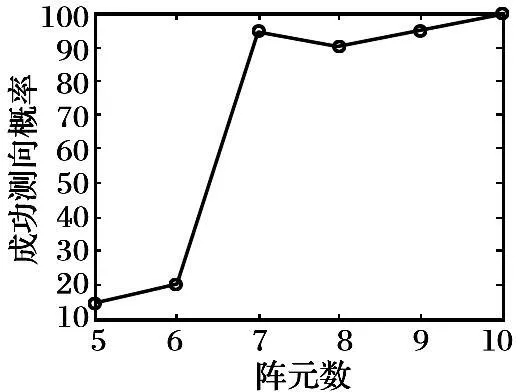
圖11　一個信號時成功測向概率與陣元數的關系曲線

圖12　一個信號時均方根誤差與陣元數的關系曲線

由圖11~12的結果可以得出， 進行單目標測向時， 隨著陣元數的增加， 成功測向概率與均方根誤差并不與之成正比， 當陣元數為7時， 成功測向概率達到95%， 而此時的測向誤差最小， 所以優先選擇7陣元。

實驗4： 兩個信號。 入射信號為最大非圓率BPSK信號， 非圓相位為10°和20°， 入射方位角為20°和30°， 俯仰角分別為80°和80°， 均勻圓陣的直徑為300 mm， 加入的每個通道相位不一致在0°~10°之間， 只考慮相鄰兩個陣元間的互耦效應， 且設兩陣元間的互耦系數為0.2557+0.1923j。 陣元數在5~10之間變化， 在每個陣元下用NC-MUSIC算法進行100次Monte-Carlo實驗， 統計不同陣元數的成功測向概率和均方根誤差結果， 如表1所示。

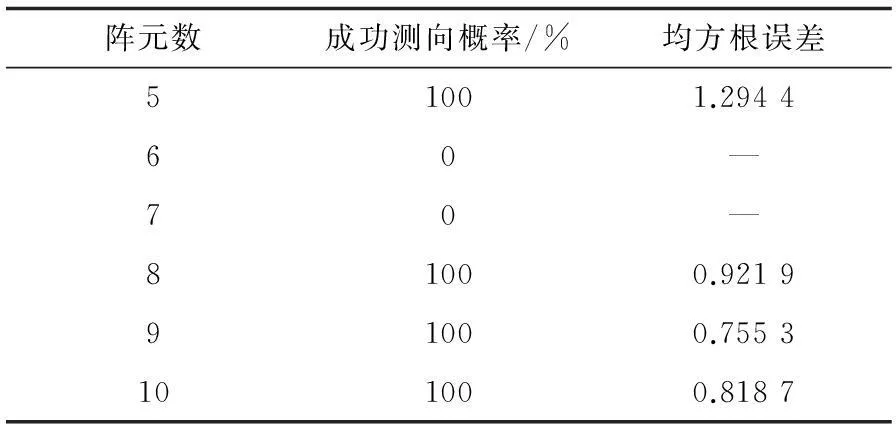
表1　成功測向概率與均方根誤差

從表1可以看出， 進行雙目標測向時， 隨著陣元數的增加， 成功測向概率并不成正比， 當陣元數為6和7時， 基本就不能夠分辨兩個信號； 當陣元數為5， 8， 9， 10時， 此時的成功測向概率達到100%， 而陣元數為9時的測向誤差最小， 則優先選擇9陣元。

5結論

本文通過對不同的天線陣列形式加入通道不一致和互耦干擾， 利用基于非圓信號的MUSIC算法來仿真最佳陣元數。 分別在均勻線陣與均勻圓陣的陣列形式下， 對單目標與雙目標進行測向模擬， 得出在有些陣列形式下使用的陣元數在加入干擾后， 測向失敗。 所以最佳陣元數的研究對避免加入干擾測向失效情況， 具有較大的幫助。

參考文獻：

[1] 楊學敏， 李廣軍， 鄭植. 基于稀疏表示的相干分布式非圓信號的參數估計[J]. 電子與信息學報, 2014, 36(1)： 164-168.

[2] 鄭春弟， 馮大政， 周祎， 等. 基于非圓信號的實值ESPRIT算法[J]. 電子與信息學報, 2008, 30(1): 130-133.

[3] 劉章孟， 周一宇， 吳海斌. 非圓信號的貝葉斯稀疏重構陣列測向方法[J]. 航空學報， 2014, 35(3): 821-827.

[4] Si Weijian, Zhu Tong, Zhang Mengying. A New Approach for Estimating the Number of Sources under the Coexistence of Circular and Various Noncircular Sources[J]. Circuits Systems, and Signal Processing, 2013, 32(6): 3107-3119.

[5] Chevalier P, Pipon F. New Insights into Optimal Widely Linear Array Receivers for the Demodulation of BPSK, MSK, and GMSK Signals Corrupted by Noncircular Interferences Application to SAIC[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 870-883.

[6] 吳向東， 張守宏， 董玫. 陣列通道不一致條件下波達方向估計及其校正[J]. 系統工程與電子技術, 2008, 30(10): 1847-1850.

[7] 周慶輝， 靳學明， 許宗澤. 超分辨測向中通道間不一致的校正[J]. 雷達科學與技術, 2006, 4(5): 280-283.

[8] 李強， 陳俊鵬， 景小榮. 多徑條件下均勻線陣DOA估計及互耦誤差自校正[J]. 電訊技術, 2012, 52(3): 314-317.

[9] Schmidt R O. Multiple Emitter Location and Signal Parameter Estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280.

[10] Zoubir A, Charge P, Wang Y. Non-Circular Sources Localization with ESPRIT[C]// European Conference on Wireless Technology, 2003: 1-4.

[11] 劉劍， 于紅旗， 黃知濤， 等. 模型誤差對非圓信號測向MUSIC算法性能的影響[J]. 電子學報， 36(12): 2280-2284.

[12] Abedia H, Delmas J P. MUSIC-Like Estimation of Direction of Arrival for Noncircular Sources[J]. IEEE Transactions on signal processing, 2006, 54(7): 2675-2690.

Study on the Optimal Sensor Numbers under the Array

Interferences Based on Non-Circular Signals

Yu Fang， Si Weijian

(College of Information and Communication Engineering， Harbin Engineering University， Harbin 150001， China)

Abstract:The problem that the direction finding performance of spatial spectrum estimation algorithm increases with the increase of sensor numbers in ideal situation, however channel disaccord and mutual coupling interferences that exist in the actual project, leading to the sensor numbers is no longer proportional to the direction finding precision, a method to study the optimal sensor numbers is proposed. Under the condition of array interferences, using the characteristics of non-circular signals’ pseudo-covariance matrix is not zero, according to the index of angle measuring accuracy and direction finding success probability, the optimal sensor numbers in uniform linear array and uniform circular array are studied based on spatial spectrum estimation algorithm, respectively. Through the simulation analysis, it is concluded that the study on optimal sensor numbers of different target numbers in different array forms is crucial for anti-interference.

Key words:array interferences； non-circular signals； the optimal sensor numbers； direction of arrival(DOA)

作者簡介：禹芳(1990-)，女，湖南衡陽人，碩士研究生，研究方向為寬帶信號檢測、處理與識別。

基金項目：航空科學基金項目(201401P6001)

收稿日期：2015-08-10

中圖分類號：TN911.7

文獻標識碼：A

文章編號：1673-5048(2015)06-0003-05