利用二次型理論精確求解雙模耦合諧振子本征能級

林 蓉

(菏澤學院 物理與電子工程系，山東 菏澤，274015)

利用二次型理論精確求解雙模耦合諧振子本征能級

林 蓉

(菏澤學院 物理與電子工程系，山東 菏澤，274015)

當兩粒子在勢場中運動時，由于兩粒子之間存在相互作用，所以體系的哈密頓量必然會多出一項相互作用的耦合項.由于此耦合項的存在，使得體系本征能級的求解出現困難.本文主要介紹利用線性代數中的二次型定理，作一個線性變換消除其中的耦合項，并且此變換也不會引起本征能級的改變，也因此使其變成一個一般的二維勢場問題，便可以精確求出其本征能級.

二次型；對角化；變換矩陣；耦合項

0 引 言

在量子力學、量子光學、分子光譜及介觀耦合電路量子化等領域，經常遇到一系列耦合諧振子問題，因此研究耦合諧振子的解顯得尤為重要，解決此類問題的關鍵是將體系的哈密頓算符對角化，進而去除耦合項.近年來，研究此問題的文獻[1-6]眾多，比如利用微擾論和坐標變換研究兩個坐標耦合諧振子的能量本征值問題[4],文獻[5]研究了3個非全同諧振子哈密頓量的退耦問題，文獻[6]研究了n模坐標耦合問題.本文利用二次型理論，通過一個線性變換消除其中的耦合項，使其變成一個一般的二維勢場問題，從而可以求出諧振子體系能量本征值的精確解.對于一般的相互作用的耦合諧振子體系的哈密頓量可表示為

其中，m為諧振子的質量，x為坐標，p為動量算符.

1 表象變換

1.1 求幺正變換矩陣

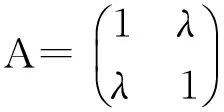
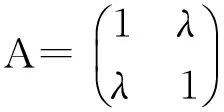
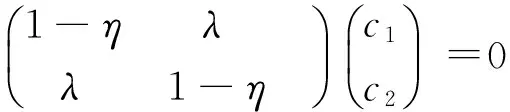
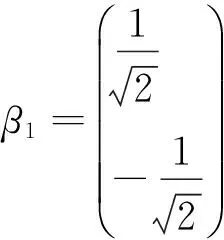
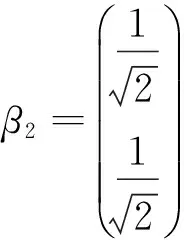
于是得幺正變換矩陣為：

(1)

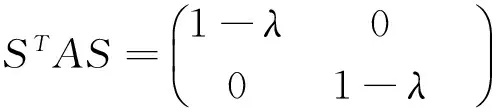
1.2 變換后的哈密頓量

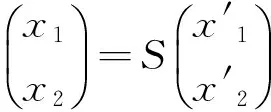
(2)

對復合函數求偏導可得：

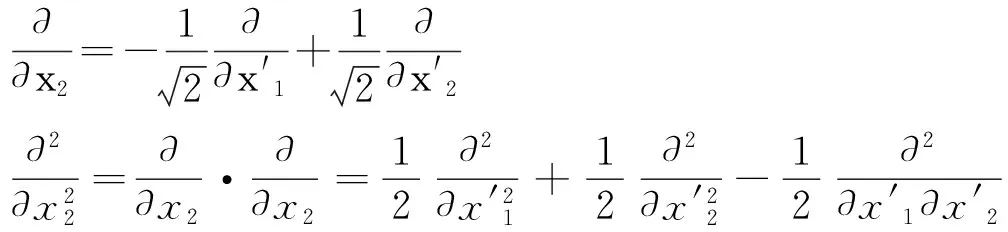
由上式復合函數的偏導可以看出：

(3)

由(2)和(3)可得：

(4)

將(4)式代入體系的哈密頓量中得

2 證明變換后表象的完備性

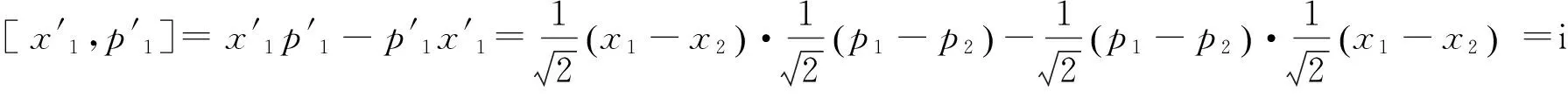
同理可得

(5)

由此證新表象滿足正交完備的關系因此可以用新表象來作變換代替原來的表象

3 體系的本征能級

3.1 體系的本征函數

變換得到的哈密頓量我們可以設體系的波函數

(6)

將(2)代入(6)中得

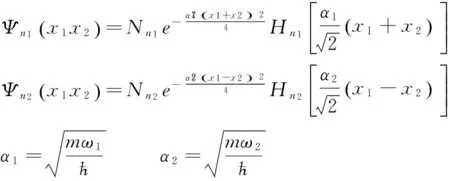
3.2 體系本征能級

所以體系哈密頓量精確求解的本征能級

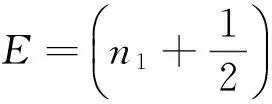
4 結 論

利用二次型定理通過表象變換可簡便的求出體系的本征能級.這為量子力學增加了新的活力.如果是n模的耦合諧振子也可以用此方法利用二次型定理求出變換矩陣通過表象變換得到n維諧振子的形式便可以很容易的求出本征能級.

[1] 琚澤志，李文波.二模諧振子能譜研究[J].大學物理，2013，32(8)：35-40.

[2] 李鳳敏.磁場中三維各向異性諧振子哈密頓量的對角化[J].物理與工程，2015,25(1)：39-43.

[3] 胡孔云，孔曌君，徐園，楊濤，等.耦合諧振子體系能譜的不變本征算符求解法[J].安徽工業大學學報(自然科學版),2013,30(2):178-181.

[4] 曾謹言. 量子力學[M].北京：科學出版社,1999.512-518.

[5] 稽英華，雷敏生.三個非全同耦合諧振子哈密頓量的退耦合[J].大學物理，2001，20(10):24-25.

[6] 逮懷新，張永德.各向異性n模耦合諧振子的精確求解[J].大學物理，2000,19(5):19-20.

[7] 同濟大學數學系.工程數學線性代數(第5版)[M].北京：高等教育出版社，2007.124-127.

[責任編輯：徐明忠]

Solving quadratic precision using mode coupling theory of intrinsic energy levels of harmonic oscillator

LIN Rong

(Department of Physics and Electronics, Heze University, Heze 274015,China)

When two particles moving in the potential field, due to the interaction between two particles. Therefore, the Hamiltonian system is bound to a more interaction coupling. Since the existence of this coupling term system will be in demand when the intrinsic difficulty level, this paper is to introduce the use of linear algebra in the secondary type theorem for a linear transform in which the coupling term, and the nature of this transformation does not lead to changes in the intrinsic energy level, and therefore it becomes a normal two-dimensional potential field problem, we can precisely calculate its intrinsic energy level

quadratic; diagonalization; transformation matrix;coupling term

2015-03-26;

2015-04-20

菏澤學院自然科學基金項目(XY13KJ04)

林蓉(1989-)，女，山東定陶人，菏澤學院助教，碩士，主要從事非線性光學方向和量子力學的研究.

O413.1

A

1672-3600(2015)06-0044-03