液力變矩器機構變量交互作用研究

王安麟,孟慶華,李文嘉,韓繼斌

?

液力變矩器機構變量交互作用研究

王安麟1,孟慶華1,李文嘉1,韓繼斌2

液力變矩器以良好的自適應性、低速穩定性等優越性被廣泛應用于車輛和工程機械。提高液力變矩器性能一直是學者研究的重要課題,而改進液力變矩器機構參數是提高性能的主要措施。

Ejiri等對液力變矩器的扁平化進行了研究并取得了一定的成果[1-2]。雷雨龍等研究了液力變矩器葉片的成型方法,并對葉型設計方法進行了改進,以有效指導液力變矩器葉柵系統的設計[3-4]。Wu等借助一體化平臺對液力變矩器葉柵系統進行了設計、分析[5]。韓克非等基于正交試驗法研究了泵輪葉片角對液力變矩器性能的影響,并對泵輪葉片角進行了優化[6]。范春順基于三維流體仿真分析了葉片數對液力變矩器性能的影響[7]。劉城等研究了葉片數對液力變矩器性能影響的顯著性,并對葉片數進行了優化,以提高液力變矩器的綜合性能[8]。

綜上,對提升液力變矩器性能的研究多為葉型的改進、葉片角的優化及葉片數的優化。液力變矩器屬于復雜的流固耦合機構,而機構變量間的交互作用對液力變矩器性能存在影響。現有的對葉片角與葉片數的優化設計采用的分步優化方法割裂了葉片角與葉片數的耦合關系,無法考慮葉片角與葉片數的交互作用。本文運用正交試驗法合理安排試驗,通過三維全流道仿真得到樣本數據,就液力變矩器性能對機構變量的靈敏度進行了分析,著重研究了葉片角與葉片數的交互作用對液力變矩器性能的影響,綜合葉片角與葉片數建立了響應曲面模型,采用多目標遺傳算法進行了優化。

1 三維流體仿真

1.1 三維流體仿真參數設定

液力變矩器屬于流道封閉的復雜流固耦合機構,隨著計算流體動力學(CFD)的迅速發展,采用CFD模擬液力變矩器內部流場的真實流動情況日漸成熟[9]。

本文采用全流道模型進行了仿真,以提高CFD仿真的準確度。液力變矩器流道模型網格劃分如圖1所示。不同葉輪間相對運動的數值解析方法主要有混合界面法、凍結轉子法和滑移網格法,對于向心式渦輪液力變矩器采用凍結轉子法較為適合[10]。通過文獻參考及仿真經驗,壓力速度耦合算法可采用SIMPLE算法,空間離散格式為一階上游迎風格式,湍流模型為RNGk-ε湍流模型[11]。

圖1 流道模型網格

1.2 三維流體仿真驗證

為驗證CFD三維仿真結果的準確性,通過臺架試驗獲得試驗數據,將試驗數據與CFD三維仿真結果進行對比。如圖2所示,在不同傳動比i下,變矩比K和泵輪扭矩系數λB的相對誤差均小于3%,效率η的絕對誤差小于5%,表明CFD三維仿真結果精度較高,可以用于研究機構變量對液力變矩器性能的影響。

圖2 CFD仿真與試驗性能參數對比

2 液力變矩器性能對機構變量的靈敏度分析

2.1 機構變量選擇

液力變矩器的機構變量包括葉片角、葉片數、葉片形狀和葉片厚度等。傳統液力變矩器優化設計過程中普遍認為,葉片進、出口角度對液力變矩器性能影響最為顯著[12],忽略了葉片數的影響,而且現有研究均未考慮葉片角與葉片數的交互作用對液力變矩器性能的影響。本文綜合葉片角與葉片數對液力變矩器性能影響進行了靈敏度分析,以泵輪作為研究對象,將泵輪入口角βB1、出口角βB2和葉片數nB及與泵輪有直接影響的渦輪入口角βW1和導輪出口角βD2作為變量進行了研究,而渦輪出口角βW2、導輪入口角βD1、渦輪葉片數nW和導輪葉片數nD不作為變量。液力變矩器原始模型的機構變量參數如表1所示。

2.2 正交試驗設計

試驗設計中對試驗指標有影響的變量稱為因子,把因子變化的各種狀態稱為因子水平。正交試驗設計是研究多因子、多水平試驗的一種高效、快速、經濟的試驗設計方法[13]。本文液力變矩器的正交試驗設計因子有βB1、βB2、nB、βW1和βD2,每個因子取4個水平(水平1～水平4),水平的選取主要參考現有液力變矩器的設計范圍[14],如表2所示。由此,選用正交表L32(49)安排試驗。

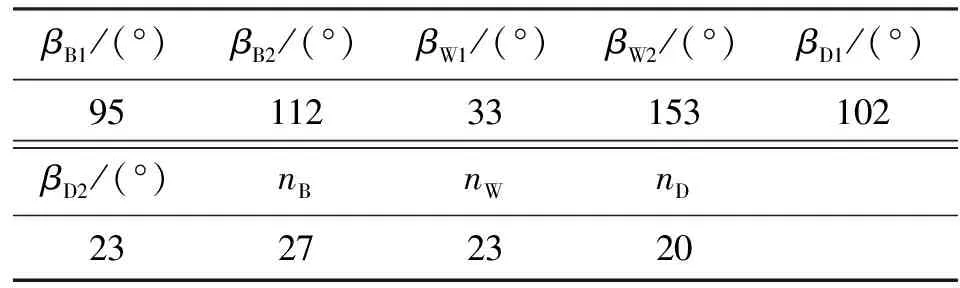
表1 液力變矩器原始模型的機構變量參數

表2 液力變矩器性能影響因子水平表

液力變矩器工作性能的評價主要有變矩性能、經濟性能和能容性能,本文研究的性能指標分別是起動變矩比K0、最高效率ηm和最高效率工況下泵輪扭矩系數λBm。根據選用的正交表建模、仿真得到樣本數據。

2.3 靈敏度分析

靈敏度分析是研究一個模型的輸出響應對輸入因子變化的敏感程度的方法。本文通過靈敏度分析確定各因子對液力變矩器性能指標的影響程度,主要包括線性相關程度、二次相關程度和因子間交互作用程度,并通過帕累托(Pareto)圖來表征。圖中橫坐標的貢獻率反映因子對性能指標影響程度的百分比,正值表示正效應,負值表示反效應。對于不同性能指標,貢獻率排在前10位的因子作用程度如圖3所示。

(a)起動變矩比

(b)最高效率

(c)最高效率工況下扭矩系數圖3 各性能指標的Pareto圖

交互效應圖反映了2個因子間的交互作用對性能指標的影響程度和關系,其繪制方式是在一個因子取不同水平的情況下,將另一因子對響應的主效應圖進行疊加而成。通過方差分析可以得到交互效應圖,如果圖中2條線不平行或交叉,則表示存在交互作用,交互作用的強弱由不平行程度反映;如果圖中2條線相互平行,則表示不存在交互作用。起動轉矩比、最高效率和最高效率工況下扭矩系數的各葉片角與泵輪葉片數交互效應圖如圖4～圖6所示。

(a)泵輪入口角與泵輪葉片數

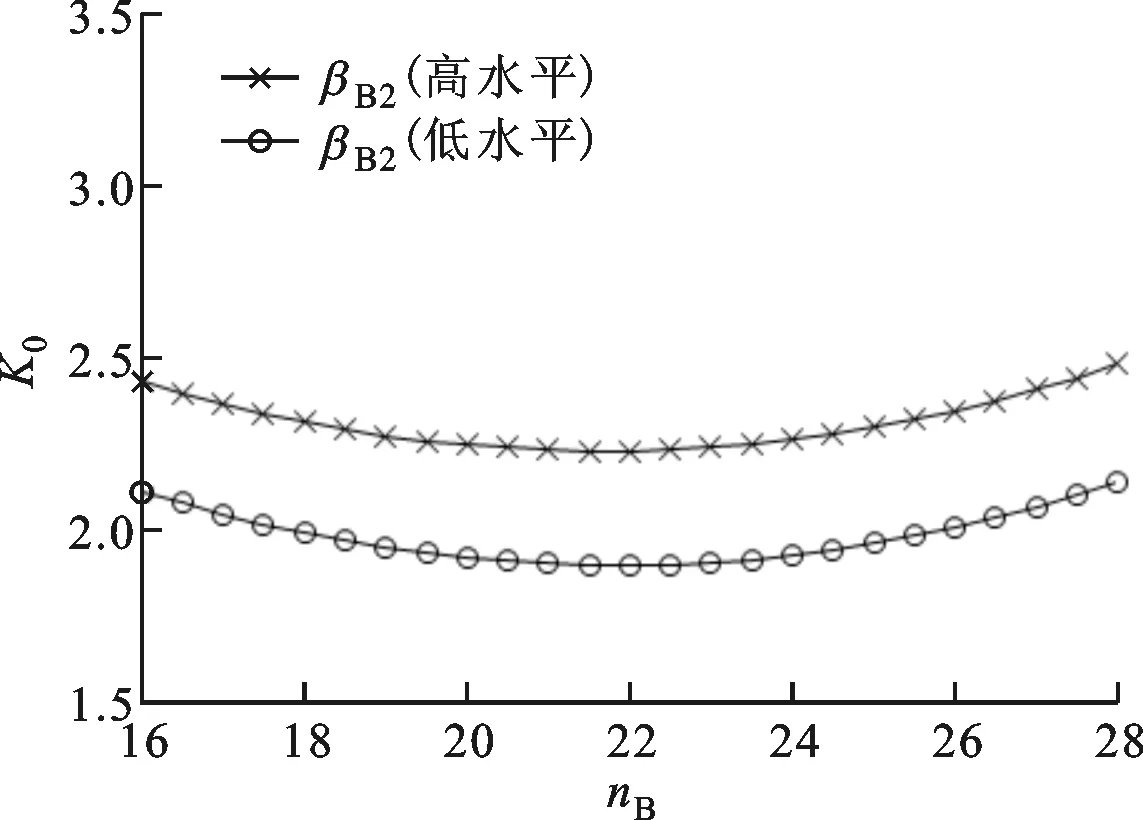
(b)泵輪出口角與泵輪葉片數

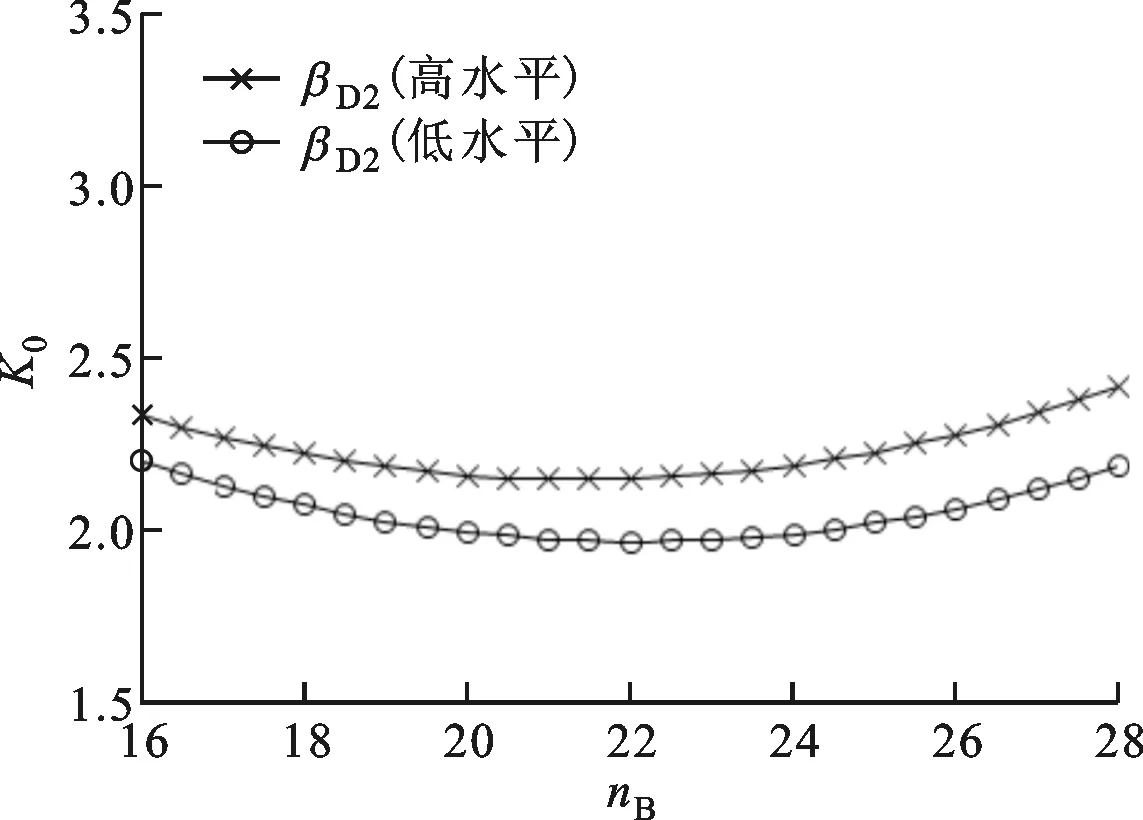
(c)導輪出口角與泵輪葉片數

(d)渦輪入口角與泵輪葉片數圖4 起動變矩比的交互效應圖

(a)泵輪入口角與泵輪葉片數

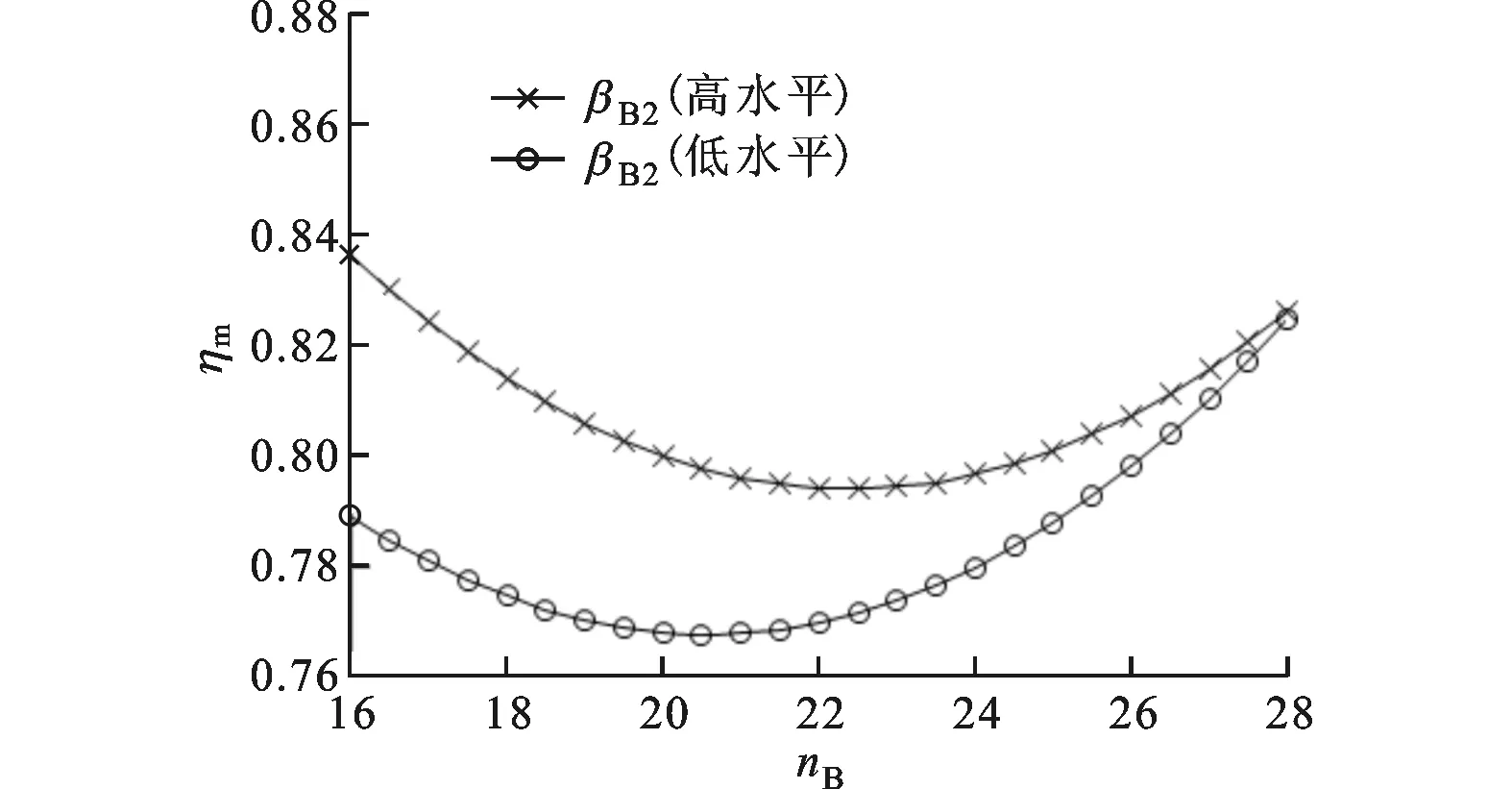
(b)泵輪出口角與泵輪葉片數

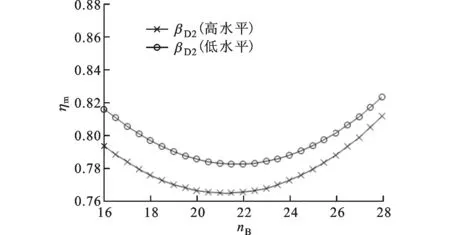
(c)導輪出口角與泵輪葉片數

(d)渦輪入口角與泵輪葉片數圖5 最高效率的交互效應圖

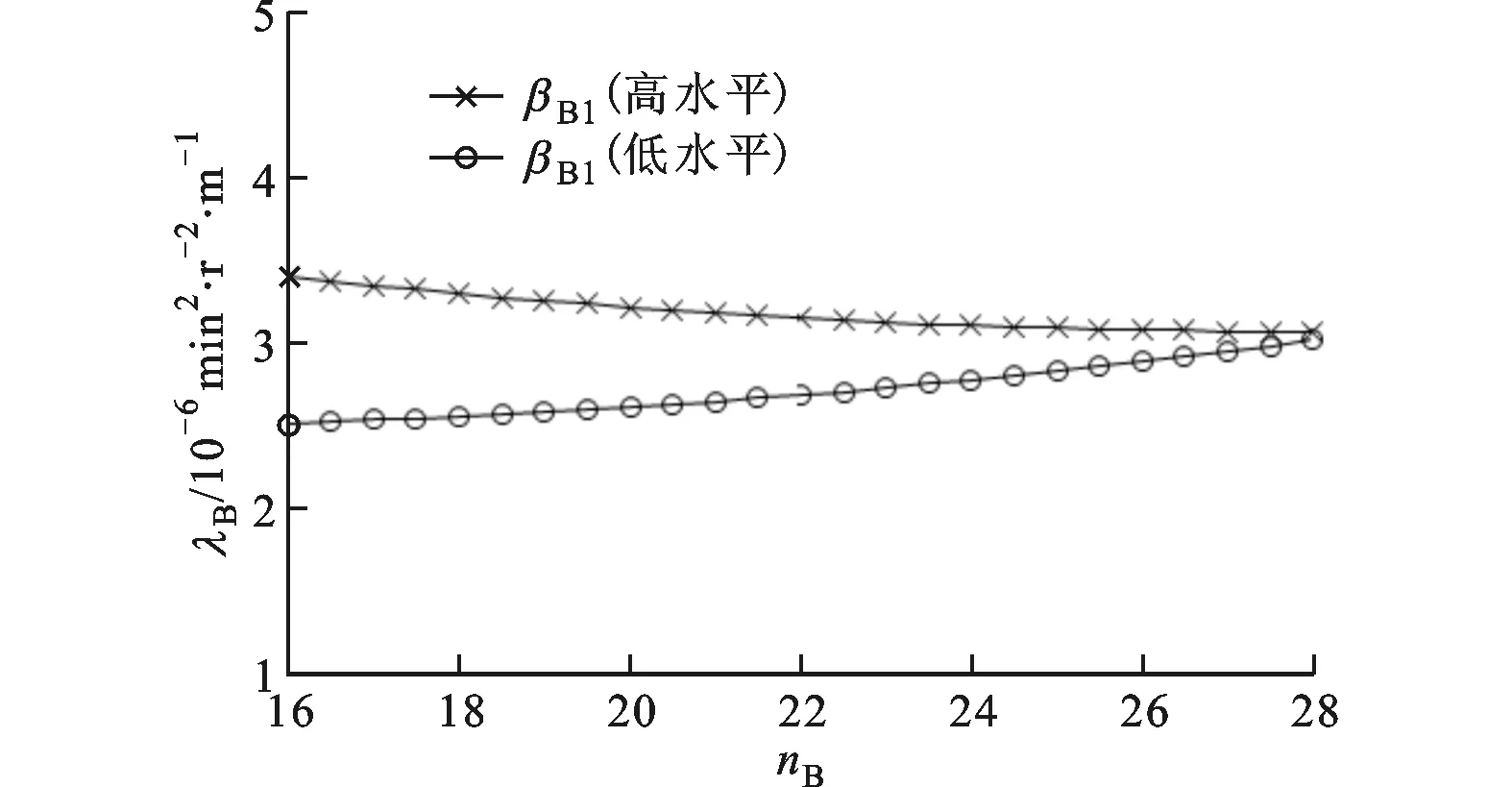
(a)泵輪入口角與泵輪葉片數

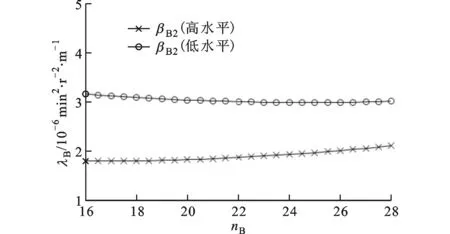
(b)泵輪出口角與泵輪葉片數

(c)導輪出口角與泵輪葉片數

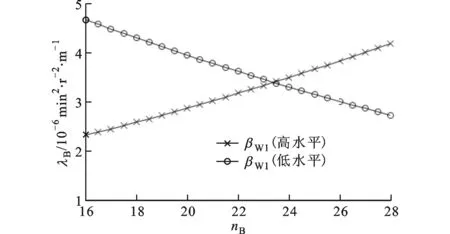
(d)渦輪入口角與泵輪葉片數圖6 扭矩系數的交互效應圖

綜上可知,泵輪葉片數與渦輪入口角的交互作用對液力變矩器性能的影響相當顯著。其原因是工作介質是從泵輪出口流向渦輪入口,而葉片數的改變會使液流偏離發生改變,從而對渦輪入口的沖擊損失產生較大影響,而渦輪入口角的改變直接影響渦輪入口處的沖擊損失,從而說明泵輪葉片數與渦輪入口角之間存在著較強的耦合關系。由上述分析還可知,相對于葉片角,葉片數對液力變矩器性能也存在顯著影響,說明傳統優化設計中認為葉片角對液力變矩器性能影響最為顯著而低估葉片數的影響是不合理的。

3 基于響應曲面法的機構變量綜合優化方法

響應曲面法(RSM)是依據樣本數據建立因子與響應的多元回歸方程以便進行優化的方法。基于響應曲面法的優化流程如圖7所示。樣本數據由機構變量參數(因子的水平)和實際響應(性能指標)組成,根據樣本數據和響應曲面模型形式可擬合響應曲面各項系數。響應曲面存在擬合誤差,如果該誤差滿足要求,則說明響應曲面模型可以進行優化,然后基于響應曲面模型采用遺傳算法尋優,將優化結果通過CFD三維仿真進行驗證;如果誤差不滿足要求,則修改響應曲面模型形式,以保證擬合精度。

圖7 基于響應曲面法的優化流程圖

3.1 響應曲面模型

響應曲面模型是采用多元回歸方程建立的因子與響應之間的函數關系。本文采用五元三次回歸方程構造響應曲面,其形式為

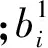
根據正交試驗仿真得到的樣本數據擬合五元三次回歸方程的系數。響應曲面模型的擬合誤差和擬合度R2如表3所示。

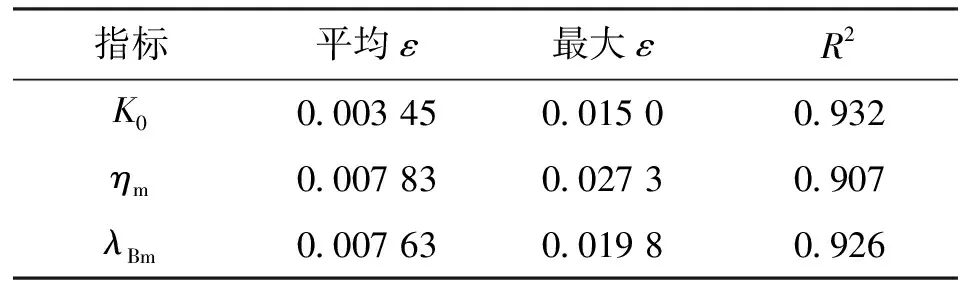
表3 響應曲面法擬合誤差分析

由表3可知,響應曲面模型的擬合誤差較小,擬合度均在0.9以上,說明利用正交試驗設計所得的樣本數據對三次響應曲面擬合精度較高,進而說明可以基于響應曲面法對液力變矩器進行優化。

3.2 機構變量綜合優化方法

由于響應曲面模型具有非線性性,為避免傳統優化方法陷入局部極值點,采用遺傳算法對響應曲面進行了優化。本文中液力變矩器性能指標有3個,其優化屬于多目標優化問題,故采用多目標遺傳算法進行優化[15]。

為比較葉片角與葉片數綜合優化和分步優化對液力變矩器性能的提升程度,將泵輪入口角、泵輪出口角、導輪出口角和渦輪入口角作為變量,采用與2.2節相同的水平取值和正交表安排試驗來獲取仿真樣本數據,通過響應曲面模型優化得到最優葉片角組合,然后單獨對泵輪葉片數進行優化。將分步優化結果和綜合優化結果通過CFD三維仿真進行了驗證。基于不同優化方法得到的機構變量參數與性能指標的對比如表4所示。

由表4可知,綜合優化方法相比于分步優化方法的起動變矩比提高了0.336,最高效率提高了2.1%,最高效率工況下泵輪扭矩系數提高了0.306×10-6min2·r-2·m-1,各項性能指標均有不同程度的提高,進一步說明了葉片角與葉片數的交互作用對液力變矩器性能影響較為顯著。

表4 基于不同優化方法得到的機構變量參數與性能指標的對比

4 結 論

(1)在對比試驗數據確認三維流體仿真的基礎上,采用正交試驗法科學、合理地安排試驗,通過全流道流體仿真得到液力變矩器性能指標,即起動變矩比、最高效率和最高效率工況下泵輪扭矩系數,從而保證了研究結果的可靠性。

(2)以泵輪作為研究對象,分析了液力變矩器性能對機構變量的靈敏度,重點研究了機構變量間的交互作用對液力變矩器性能影響的顯著性,研究表明:泵輪葉片數對液力變矩器性能的影響較為突出,其顯著性要高于某些葉片角;渦輪入口角與泵輪葉片數的交互作用對液力變矩器的性能指標均有較為顯著影響。

(3)運用響應曲面法建立了具有較高逼近精度的五元三次響應曲面模型。基于所建響應曲面模型,采用多目標遺傳算法進行了優化,并對比了不考慮葉片角與葉片數交互作用的分步優化結果,從而驗證了葉片角與葉片數綜合優化方法可以提升液力變矩器的性能,進一步說明了機構變量間的交互作用對液力變矩器性能具有顯著影響。

[1] EJIRI E, KUBO M. Influence of the flatness ratio of an automotive torque converter on hydrodynamic performance [J]. ASME Journal of Fluids Engineering, 1999, 121(3): 614-620.

[2] KIM G, JANG J. Effects of stator shapes on hydraulic performances of an automotive torque converter with a squashed torus [C]∥SAE 2002 World Congress. Washington, DC, USA: SAE, 2002: 155-160.

[3] 雷雨龍, 王健, 胡廷輝, 等. 液力變矩器葉柵動量矩分配規律 [J]. 吉林大學學報: 工學版, 2009, 39(4): 880-884. LEI Longyu, WANG Jian, HU Tinghui, et al. Angular of momentum distribution on blades of hydraulic torque converter [J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(4): 880-884.

[4] 王立軍, 吳光強, 王歡. 基于葉片角變化規律的液力變矩器改型設計法 [J]. 同濟大學學報: 自然科學版, 2011, 39(11): 1673-1679. WANG Lijun, WU Guangqiang, WANG Huan. Design strategy for modification of torque converters based on variation law of blade angle [J]. Journal of Tongji University: Natural Science Edition, 2011, 39(11): 1673-1679.

[5] WU Guangqiang, YAN Peng. System for torque converter design and analysis based on CAD/CFD integrated platform [J]. Chinese Journal of Mechanical Engineering: English Edition, 2008, 21(4): 35-39.

[6] 韓克非, 吳光強, 王立軍. 基于正交設計的泵輪葉柵關鍵參數對液力變矩器的性能影響優化分析 [J]. 中國電機工程學報, 2010, 30(35): 65-70. HAN Kefei, WU Guangqiang, WANG Lijun. Performance optimization analysis of the effects of pump cascade key parameters on torque converter based on orthogonal design [J]. Proceedings of the CSEE, 2010, 30(35): 65-70.

[7] 范春順. 液力變矩器葉片數對其性能影響的研究 [D]. 長春: 吉林大學, 2007.

[8] 劉城, 潘鑫, 閆清東, 等. 基于DOE及RSM的液力變矩器葉片數對性能的影響及優化 [J]. 北京理工大學學報, 2012, 32(7): 689-693. LIU Cheng, PAN Xin, YAN Qingdong, et al. Effect of blade number on performance of torque converter and its optimization based on DOE and response surface methodology [J]. Transactions of Beijing Institute of Technology, 2012, 32(7): 689-693.

[9] 方杰, 齊迎春, 馬文星, 等. 液力變矩器流場的數值模擬與分析 [J]. 同濟大學學報: 工學版, 2005, 33(5): 673-677. FANG Jie, QI Yingchun, MA Wenxing, et al. Simulation and analysis of flow field in hydrodynamic torque converter [J]. Journal of Tongji University: Natural Science Edition, 2005, 33(5): 673-677.

[10]JUNG J H, KANG S, HUR N. A numerical study of a torque converter with various methods for the accuracy improvement of performance prediction [J]. Progress in Computational Fluid Dynamics, 2011, 11(3): 261-268.

[11]劉春寶, 馬文星, 朱喜林. 液力變矩器三維瞬態流場計算 [J]. 機械工程學報, 2010, 46(14): 161-166. LIU Chunbao, MA Wenxing, ZHU Xilin. 3D transient calculation of internal flow field for hydrodynamic torque converter [J]. Chinese Journal of Mechanical Engineering, 2010, 46(14): 161-166.

[12]馬文星. 液力傳動與設計 [M]. 北京: 化學工業出版社, 2004: 182-184.

[13]田中玄一. 實驗設計法概論 [M]. 北京: 兵器工業出版社, 1990: 9-12.

[14]朱經昌. 液力變矩器的設計與計算 [M]. 北京: 國防工業出版社, 1991: 74-75.

[15]YADAV O P, RATHOD V, RATHORE A, et al. Optimizing reliability-based robust design model using multi-objective genetic algorithm [J]. Computers & Industrial Engineering, 2013, 66(2): 301-310.

[本刊相關文獻鏈接]

王安麟,孟慶華,曹巖,等.液力變矩器的葉片數神經網絡模型.2015,49(7):11-16.[doi:10.7652/xjtuxb201507003]

李大海,李天石.非均勻采樣系統的支持向量回歸建模與控制.2011,45(3):65-69.[doi:10.7652/xjtuxb201103012]

宮武旗,伍儒康.求解流線曲率法反命題的一種新型有限差分方法.2015,49(3):11-13.[doi:10.7652/xjtuxb201503002]

燕浩,劉梅清,梁興,等.大型軸流泵空化特性的數值模擬.2014,48(11):44-50.[doi:10.7652/xjtuxb201411008]

張明宇,王永生,靳栓寶,等.噴水推進泵壓力脈動特性數值計算及分析.2014,48(11):51-57.[doi:10.7652/xjtuxb2014 11009]

李學臣,席光.離心葉輪出口流動分離區影響因素的數值研究.2013,47(9):16-22.[doi:10.7652/xjtuxb201309003]

(編輯 苗凌)

(1.同濟大學機械與能源工程學院,201804,上海;2.山推工程機械股份有限公司,272073,山東濟寧)

為解決現有液力變矩器機構變量優化設計中采用分步優化方法存在的問題,通過對比臺架試驗數據確認了三維流體仿真結果的準確性,運用正交試驗、通過全流道流體仿真得到了起動變矩比、最高效率和最高效率工況下泵輪扭矩系數;采用方差分析法研究了機構變量間的交互作用對液力變矩器性能影響的顯著性,在考慮交互作用的基礎上建立了五元三次響應曲面模型且應用多目標遺傳算法進行了優化。研究表明:機構變量間交互作用顯著影響著液力變矩器的性能,采用機構變量綜合優化方法優化后,起動變矩比提高了0.336,最高效率提高了2.1%,最高效率工況下泵輪扭矩系數提高了0.306×10-6min2·r-2·m-1。

液力變矩器;機構變量;交互作用;顯著性;響應曲面模型

Study on Mechanism Variables Interaction of Torque Converter

WANG Anlin1,MENG Qinghua1,LI Wenjia1,HAN Jibin2

(1. School of Mechanical Engineering, Tongji University, Shanghai 201804, China;2. Shantui Construction Machinery Co., Ltd., Jining, Shandong 272073, China)

In order to solve the problem caused by the separated step optimization for the design of the mechanism variables of torque converter, the significance of mechanism variables interaction was studied. Firstly, the accuracy of three dimensional fluid simulation results was confirmed in comparison with the bench test data. Secondly, starting torque ratio, highest efficiency and pump wheel torque coefficient at the transmission ratio of highest efficiency were obtained through full flow passages simulation based on the orthogonal experiments, and the significance of mechanism variables interaction was discussed through analysis of variance. Finally, the ternary quintic response surface model was established and optimized by using multi-objective genetic algorithm. The experiment results showed that mechanism variables interaction significantly affected torque converter performance and after optimization using the integrated optimization method of mechanism variables, starting torque ratio increased by 0.336, highest efficiency increased by 2.1%, and pump wheel torque coefficient at the transmission ratio of highest efficiency increased by 0.306×10-6min2·r-2·m-1.

torque converter; mechanism variables; interaction; significance; response surface model

2014-12-23。 作者簡介:王安麟(1954—),男,教授,博士生導師。 基金項目:2012年國家重大科技成果轉化資助項目(〔2012〕258號)。

時間:2015-06-17

http:∥www.cnki.net/kcms/detail/61.1069.T.20150617.0902.008.html

10.7652/xjtuxb201509001

TH137.332

A

0253-987X(2015)09-0001-07