一種改進的快速壓縮跟蹤算法

潘 磊，束 鑫，祁云嵩

(江蘇科技大學計算機科學與工程學院，江蘇鎮江212003)

目標跟蹤，也稱視覺跟蹤，是計算機視覺領域的一個熱點問題，在視頻監控、人機交互、視頻壓縮、行為分析等方面具有廣泛的應用價值［1-2］.在跟蹤過程中，首先通過人工在視頻首幀選擇出目標，其次對目標進行建模，然后利用預測或優化算法估計目標的下一幀位置，并對目標模型進行更新，從而進入迭代過程.傳統的目標跟蹤算法包括確定性方法和統計性方法，兩者的代表分別為Mean Shift和粒子濾波.確定性方法計算量小，實時性高，但準確性相對較低;統計性方法計算量大，準確性高，但實時性相對較低［3-4］.

近年來，目標跟蹤算法得到了眾多的關注和研究.例如，文獻［5］中提出一種基于超像素的鑒別外觀模型，使用超像素中捕獲的結構信息生成目標特征，較好解決了目標遮擋和漂移問題;文獻［6］中將目標跟蹤表達為結構化多任務稀疏學習問題，對目標遮擋、光照變化、姿態變形等具有較好的效果，并有效降低了粒子濾波計算的復雜度;文獻［7］中將圖像分割與目標跟蹤相結合，采用像素空間與顏色特征，同時解決了跟蹤與分割兩類問題;文獻［8］中提出一種基于壓縮感知的跟蹤算法，將目標高維特征投影到低維空間，提高了跟蹤的實時性，并具有較高的準確性.雖然研究取得了較快的進展，但由于噪聲、遮擋、光照、運動等不利因素的影響，解決目標跟蹤問題仍然存在許多困難.

1快速壓縮跟蹤算法

1.1 壓縮感知

不完備線性測量信號的重建與高維特征的降維一直是模式識別領域的基本研究方向.壓縮感知［9-14］是近年來出現的一種新型采樣理論，能夠在遠遠小于奈奎斯特采樣頻率的條件下還原初始信號，得到了學術界的廣泛關注.

高維信號采樣的過程可以由式(1)表示:

式中:x為K稀疏的n維原始信號;y為m維的采樣信號;Φ為m×n的觀測矩陣.根據壓縮感知理論，當n?m時，如果Φ滿足有限等距性質(restricted isometry property，RIP)，則采樣y可以有很高的概率重建信號x，均勻分布矩陣、隨機高斯矩陣、隨機貝努利矩陣等都是滿足有限等距性質的矩陣，然而，這些矩陣包含的非零元素較多，運算量較大，實際計算時，經常采用以下符合有限等距性質且具有稀疏特征的矩陣，如式(2)所示.

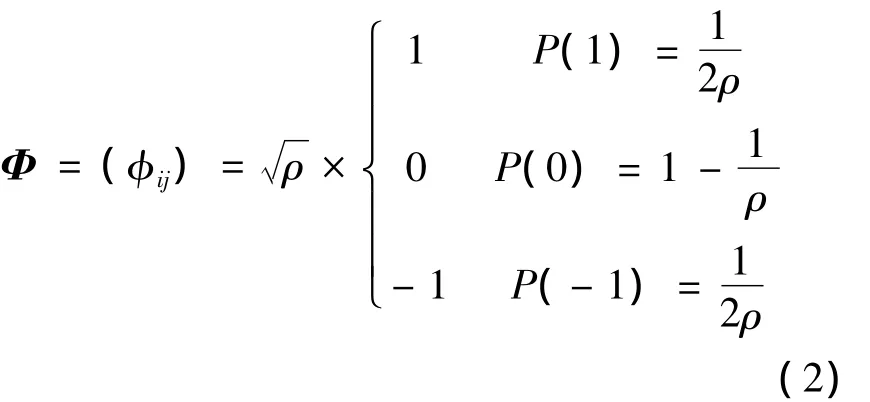
1.2 快速壓縮跟蹤算法

通過上文描述可以看出，壓縮感知技術可以在降低信號維數的同時，基本保留原有信號的全部特性，從而能夠在不降低計算精度的前提下，大大提高運算的效率.文獻［8］中將壓縮感知思想引入目標跟蹤領域，首先按照下式構造各向異性的均值濾波器:

式中:w和h為目標的寬和高，將濾波器與目標進行卷積后，生成目標的高維特征，然后使用式(2)的觀測矩陣將目標高維特征壓縮到低維空間，生成對應的目標低維特征，最后，通過貝葉斯分類器對各候選目標進行分類，選擇分類器輸出最大值所對應的候選目標作為下一幀中的目標，并更新分類器.

實驗中發現，在各向異性均值濾波器的使用中，將模板內的所有像素按照相同的重要性權值進行計算;而實際中，往往是靠近模板中心點的像素應該賦予更高的權值，遠離模板中心點的像素賦予較低的權值，并且，當濾波器的尺度超出一定的范圍時，濾波產生的新圖像已失去原始圖像的大部分信息，如圖1所示，此時，將這些新圖像作為目標特征，效果并不顯著.

圖1 多尺度濾波效果Fig.1 Results of multi-scale filtering

2 改進的快速壓縮跟蹤算法

2.1 利用多種多尺度濾波器生成目標高維特征

由上文分析可以看出，單純使用各向異性均值濾波器產生目標高維特征存在一定的缺陷，不僅降低了模板臨近中心點像素的權值，而且超過一定的尺度后，濾波產生的新圖像失去了原始目標的大部分特征.針對以上問題，文中提出一種改進的策略，在目標高維特征生成過程中，不僅使用各向異性均值濾波器，同時增加圓形均值濾波器、中值濾波器、高斯濾波器、log濾波器對目標進行濾波，共同生成目標高維特征，并且，在濾波過程中，各濾波器的尺度限制在原始目標尺度的50%范圍內，具體如式(4)所示:

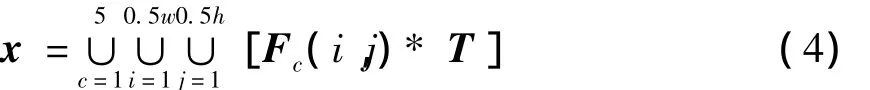
式中:x為目標高維特征;F為濾波器;i和j分別為濾波器的寬和高;w和h分別為目標的寬和高;T為目標;符號“*”為卷積;符號“∪”為連接操作，用于將卷積后生成的新圖像連接起來生成目標高維特征.

與文獻［8］中單純使用各向異性均值濾波器相比，改進的方法使用了5種濾波器，考慮了對模板像素臨近中心點和遠離點不同權值分配的衡量，能夠對目標特征進行更加準確和全面的描述.通過控制濾波器的尺度，各種濾波器單獨產生的濾波圖像數量變為文獻［9］中的25%，但由于采用了5種濾波器，濾波圖像的總數量，即目標高維特征維數不降反升，超出了文獻［8］中數量的25%，因此更多的保留了原始圖像的信息.

2.2 基于壓縮感知理論生成目標低維特征

得到目標高維特征后，采用壓縮感知理論生成目標低維特征.文獻［9］中證明，對于式(2)，采用ρ=能夠獲得較快的運算速度，且準確性幾乎不會降低.然而，對目標圖像經過多尺度濾波后生成的高維特征，n的數量級可以達到106以上，此時觀測矩陣Φ中非零元的數量仍然較多.文中采用文獻［8］中的方法，令ρ=n/lg n，此時雖然準確性會有所降低，但Φ中非零元的數量得到了指數級的下降，因此計算速度得到顯著提升.

當n的數量級為10d時，Φ中非零元的數量約為md，即每行有d個非零元，實際計算時，只需記住這些非零元的位置和數值即可.因此，目標低維特征y的生成速度是相當快的.

2.3 目標與候選目標相似性度量

獲得目標與候選目標的低維特征后，下一步的工作就是采用相似性度量比較目標與候選目標之間的差異.文獻［8］中通過貝葉斯分類器進行判斷，選擇分類器最大響應值對應的候選目標作為下一幀的目標.然而，由于在高維特征構造過程中各向異性均值濾波器存在缺陷，分類器的分類效果受到一定的影響.針對此問題，引入Bhattacharyya系數進行改進.

首先，假設候選目標為正負樣本的概率相同，采用貝葉斯分類器對候選目標進行分類計算，如式(5)所示.

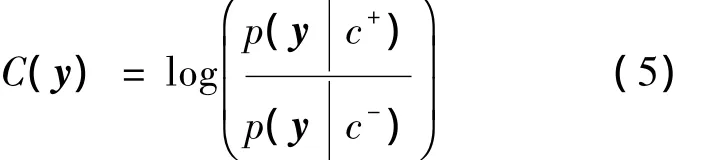
式中:c+為正樣本;c－為負樣本.分類器的更新策略按照文獻［8］的方法進行.

其次，采用Bhattacharyya系數計算目標與候選目標之間的相似度，如式(6)所示.

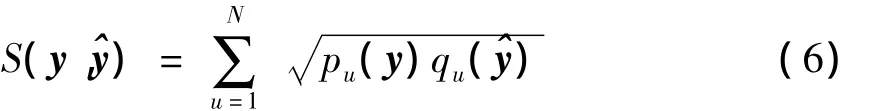
式中，y為目標;y^為候選目標;p和q分別為y和y^的概率分布.

得到候選目標的貝葉斯分類器輸出及其與目標之間的Bhattacharyya相似度后，以兩者的乘積作為目標與候選目標之間最終的相似程度，并選擇最大值所對應的候選目標作為下一幀的目標，如式(7)和式(8)所示.

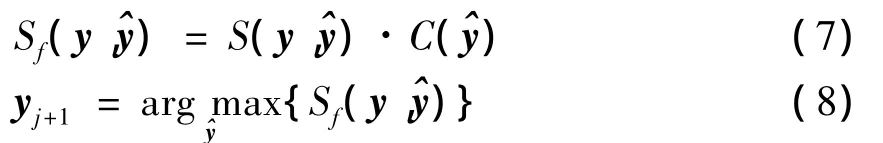
2.4 算法流程

根據以上描述，得到改進的快速壓縮跟蹤算法流程如下:①根據式(4)計算當前幀目標和下一幀對應位置的δ鄰域范圍內所有候選目標的高維特征;②利用式(2)的觀測矩陣，通過式(1)將①中所有的高維特征投影到低維空間，得到對應的低維特征;③根據式(5～7)計算候選目標與目標之間的相似度，并按照式(8)取相似度最大的候選目標作為下一幀的目標;④更新分類器，進入下一次迭代.

3 實驗結果與分析

實驗在Intel Core i5 M480CPU，4GB內存的筆記本電腦進行，采用Matlab 2013b編程，測試的6段視頻來源于 MILT視頻庫［15］和 LOT視頻庫［16］.采用 PASCAL 指標［8，16-17］衡量跟蹤算法性能，如式(9)所示.

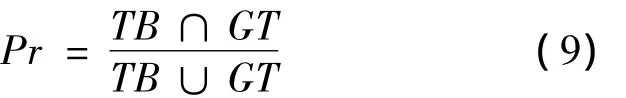
式中:TB為跟蹤算法目標邊界框;GT為真實目標邊界框.當兩者完全重疊時，Pr取值為1，當兩者完全不重疊時，Pr取值為0，一般當Pr取值大于0.5時，認為跟蹤成功.

改進算法的實驗結果包括定性分析和定量分析兩個部分.圖2～5列舉了算法在部分視頻庫上跟蹤的定性結果.表1列舉了算法在視頻庫上跟蹤的定量結果以及與常用的 MILT［15］，TLD［18］和FCT［8］算法比較的結果.

由圖2～5可以看出，文中提出的改進算法在光照、遮擋、運動、變形等不利因素的干擾下，能夠較準確跟蹤各種目標.表1中，粗體顯示的數字表示對應視頻中的跟蹤效果最好.從表1的對比可以看出，文中算法與常用跟蹤算法相比，在準確率上具有一定的優勢，在5段視頻的跟蹤上取得最高的準確率;TLD算法在最后一個視頻中取得最高的準確率.

圖2 David序列部分跟蹤結果Fig.2 Partial results of tracking David sequence

圖3 Football序列部分跟蹤結果Fig.3 Partial results of tracking Football sequence

圖4 Girl序列部分跟蹤結果Fig.4 Partial results of tracking Girl sequence

圖5 Faceocc序列部分跟蹤結果Fig.5 Partial results of tracking Faceocc sequence

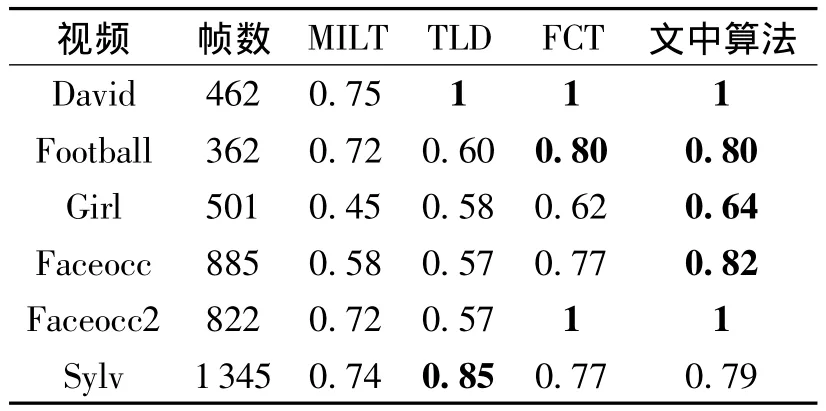
表1 各算法PASCAL指標Table 1 PASCAL index of each algorithm

經分析發現，算法在目標發生較大遮擋、運動和形變時，容易出現跟蹤錯誤的情況.例如，Football視頻中從287幀開始，跟蹤的目標產生嚴重遮擋，且遮擋物體的特征與目標的特征幾乎完全相似，于是產生跟蹤錯誤，跟蹤的目標由原目標轉移到了遮擋物體上，如圖6所示;Sylv視頻中從第896幀開始，跟蹤的目標出現較大的運動和形變，跟蹤逐步出現誤差，直至929幀出現PASCAL指標低于0.5的情況，然而，隨著運動與形變的逐漸減弱，從965幀開始PASCAL指標逐步恢復到0.5以上，并重新準確跟蹤目標，如圖7所示.

圖6 Football視頻跟蹤錯誤的幀Fig.6 Falsely tracked frames in Football video

圖7 Sylv視頻跟蹤錯誤的幀Fig.7 Falsely tracked frames in Sylv video

4 結論

根據快速壓縮跟蹤算法存在的問題，在目標高維特征生成過程中，引入多種多尺度濾波器與原始目標進行卷積，不僅保留了目標盡可能多的信息，并且通過限制濾波器尺度的范圍，避免了無效信息對算法的影響，同時，由于多種濾波器的使用，目標有效信息的維數得到了一定的提高，為后續跟蹤的準確進行奠定了基礎.按照壓縮感知理論，經過觀測矩陣采樣后生成的目標低維特征保留了目標幾乎所有的信息，然后通過貝葉斯分類器輸出與Bhattacharyya系數乘積的形式，完成下一幀目標位置的計算，在一定程度上抵消了分類器產生的誤差.下一步的工作，將圍繞高維特征模型展開，解決目前算法對較大遮擋、運動和形變敏感的缺點，這也是目標跟蹤領域研究的主要困難之一.

References)

［1］ Li Xi，Hu Weiming，Shen Chunhua，et al.A survey of appearance models in visual object tracking［J］.ACM Transactions on Intelligent Systems and Technology，2013，4(4):58.

［2 ］ Guo Yanwen，Chen Ye，Tang Feng，et al.Object tracking using learned feature manifolds［J］.Computer Vision and Image Understanding，2014，118:128-139.

［3］ 王新紅，王晶，田敏，等.基于空間邊緣方向直方圖的Mean Shift跟蹤算法［J］.中國圖象圖形學報，2008，13(3):586-592.Wang Xinhong，Wang Jing，Tian Min，et al.Mean shift tracking algorithm based on spatial edge orientation histograms［J］.Journal of Image and Graphics，2008，13(3):586-592.(in Chinese)

［4］ 初紅霞，謝忠玉，王君祥，等.空間相關背景加權直方圖均值漂移目標跟蹤［J］.控制與決策，2014，29(3):528-532.Chu Hongxia，Xie Zhongyu，Wang Junxiang，et al.Mean shift target tracking with spatiogram corrected background-weighted histogram［J］.Control and Decision，2014，29(3):528-532.(in Chinese)

［5］ Yang Fan，Lu Huchuan，Yang M H.Robust superpixel tracking［J］.IEEE Transactions on Image Processing，2014，23(4):1639-1651.

［6］ Zhang Tianzhu，Ghanem Bernard，Liu Si，et al.Robust visual tracking via structured multi-task sparse learning［J］.International Journal of Computer Vision，2013，101(2):367-383.

［7］ Papoutsakis K E，Argyros A A.Integrating tracking with fine object segmentation［J］.Image and Vision Computing，2013，31:771-785.

［8］ Zhang Kaihua，Zhang Lei，Yang M H.Fast compressive tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2014，36(10):2002-2015.

［9］ Li P，Hastie T J，Church K W.Very sparse random projections［C］∥Proceedings of the 12th International Conference on Knowledge Discovery and Data Mining，［S.l.］:ACM，2006:287-296.

［10］ Strohmer T.Measure what should be measured:progress and challenges in compressive sensing［J］.IEEE Signal Processing Letters，2012，19(12):887-893.

［11］ Qaisar S，Bilal R M，Iqbal W，et al.Compressive sensing:from theory to applications，a survey［J］.Journal of Communications and Networks，2013，15(5):443-456.

［12］ Engelberg S.Compressive sensing［J］.IEEE Instrumentation ＆ Measurement Magazine，2012，15(1):42-46.

［13］ Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289-1306.

［14］ Friedland S，Li Q，Schonfeld D.Compressive sensing of sparse tensors［J］.IEEE Transactions on Image Processing，2014，23(10):4438-4447.

［15］ Babenko B，Yang M H，Belongie S.Robust object tracking with online multiple instance learning［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33(8):1619-1632.

［16］ Shaul O，Aharon B H，Dan L，et al.Locally orderless tracking［J］.International Journal of Computer Vision，2014.

［17］ Everingham M，Gool L，Williams C，et al.The Pascal visual object classes(VOC)challenge［J］.International Journal of Computer Vision，2010，88(2):303-338.

［18］ Kalal Z，Mikolajczyk K，Matas J.Tracking learning detection［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34(7):1409-1422.