基于遺傳算法的應急物資分層調度研究

胡飛虎，田朝暉，李 威，韓 鑫

（西安交通大學電氣工程學院工業自動化系，西安 710049）

基于遺傳算法的應急物資分層調度研究

胡飛虎，田朝暉，李 威，韓 鑫

（西安交通大學電氣工程學院工業自動化系，西安 710049）

針對多車型、多物資特征的應急物資調度問題，設計分層調度方案，同時給出由兩層物資調度系統組成的調度算例，并將該算例轉化為2個相關的單層物資調度問題。以最小化系統調度任務完成時間為目標函數，利用遺傳算法對一級和二級調度方案進行求解，得出系統中每種車型依次將何種貨物從何地運往何處的具體方案。通過車輛各自運輸任務的運貨量計算和倉庫點物資的實時統計結果表明，該分層調度方案符合各倉庫出貨量不超過現存量且各災害點物資需求得到滿足的供求條件，求解步驟簡單且運行速度快。

應急物資調度；分層調度；車輛調度；遺傳算法；目標函數

1 概述

啟發式優化算法［1］被廣泛用于解決應急物資配送的車輛調度［2-4］問題。在物資調度問題的求解方面：文獻［5］應用蟻群算法對調度問題進行優化，將原始物資分配分為2個階段，車輛路線分配和多種物資分配，從而解決應急物資運輸問題。文獻［6］在多種商品、多配送情況下，以系統總成本最小為目標，建立兩階段混合整數規劃模型解決物資調度問題。文獻［7］提出一種混合模糊聚類算法，得出關聯兩路網下物資調度問題的求解方案。文獻［8］給出供應與需求不平衡情況下兩階段的多種運輸方式、多物資運輸模型。文獻［9］提出兩階段隨機規劃方法解決調度問題。文獻［10］針對應急物資調度問題，建立情景響應式兩階段隨機規劃模型。文獻［11］研究了供應鏈中傳統的車輛路徑問題以及多

物資網絡流問題，并且在交通工具、物資變化等情況下，提出解決動態調度問題的算法。分層是指路網調度具有層次，如省級路網、地方路網以及各種路網上適用的運輸工具，本文提出對此類調度問題進行求解的思路。每層的需求點為下層的倉庫點，各層的運輸工具僅需完成各自所在層的倉庫到需求點的物資調度任務，這樣即可依次對各層調度問題進行獨立求解，從而簡化問題，便于求解計算。物資兩層調度問題是此問題的典型特例，在實際問題中由二級調度（市縣級地方倉庫至災害點）和一級調度（國家、省級倉庫至市縣級地方倉庫）組合成的兩層調度問題。因此，本文提出物資兩層調度問題的數學模型，以任務耗時最短為目標，利用遺傳算法［12-14］和分層求解方法給出最優調度方案。

2 兩層應急物資調度問題的數學模型

已知各倉庫點的物資儲量和災害點的物資需求量。

（1）假設條件

1）各層調度系統的運輸工具只負責完成各自所在層的物資調度任務。

2）一級倉庫點和二級倉庫點各物資的總存儲量一定能滿足災害點對各物資的總需求量，且二級倉庫有一定儲量，保證不會中途空倉，導致二級車輛在該二級倉庫等待。

3）不考慮各運輸工具的裝卸貨時間。

4）各運輸工具的初始停放地點可為倉庫點，也可為災害點，且在執行完某單次任務后不必回到初始出發地點。

5）各運輸工具均滿載某單一物資正常運行，不考慮物資的混合裝載且一旦開始執行某次運輸任務，不能中途退出。

（2）模型參數

W：應急物資集合，即W=｛w1，w2，…，wP｝。

B：一級倉庫點集合，即B=｛b1，b2，…，bm｝。

C：二級倉庫點集合，即C=｛c1，c2，…，ca｝。

E：災害點集合，即E=｛e1，e2，…，eq｝。

BW：一級物資儲備中心（一級倉庫）物資信息集合，即BW=｛bw1，bw2，…，bwm｝。

CW：二級物資儲備中心（二級倉庫）物資信息集合，即CW=｛cw1，cw2，…，cwn｝。

EW：災害救援中心（災害點）物資信息集合，即EW=｛ew1，ew2，…，ewa｝，ewk（k=1，2，…，a）表示某個災害點的物資信息，包括需要的物資類型（wf）（f=1，2，…，P）及相應的需求量（γkf），即 ewk=｛（w1，γk1），（w2，γk2），…，（wP，γkP）｝。

R：一級運輸工具信息集合，即 R=｛r1，r2，…，rg｝。rk（k=1，2，…，g）表示一級運輸工具信息，包含載貨量（dk）、速度（sk）、數量信息（nk），即 rk=｛dk，sk，nk｝。N=｛n1，n2，…，ng｝，nk（k=1，2，…，g）表示一級某種類型的運輸工具的數量。

V：二級運輸工具信息集合，即 V=｛ν1，ν2，…，νh｝，νk（h=1，2，…，y）表示二級運輸工具信息，包含載貨量（dk）、速度（sk）、數量信息（nk），即 νk=｛dk，sk，nk｝，N=｛n1，n2，…，nh｝，nk（k=1，2，…，h）表示二級序列某種類型的運輸工具的數量。

q為一級倉庫點和二級倉庫點間路徑距離矩陣：

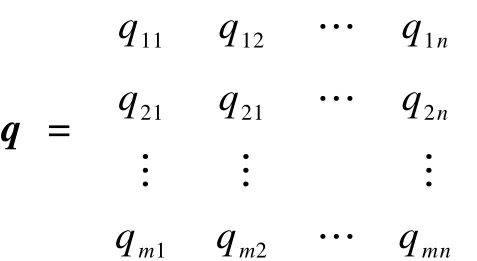
l為二級倉庫點和災害點之間的路徑距離矩陣：

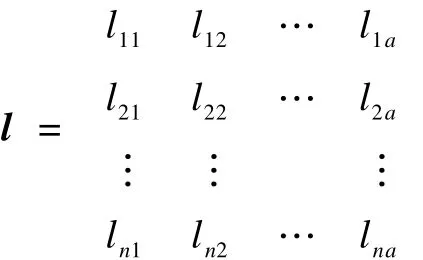
μ：一級車輛的一次完整運載任務，即 μ=（bi，wf，cj）（i=1，2，…，m；f=1，2，…，P；j=1，2，…，n）。一級車輛的一次完整運載任務包括出發一級倉庫點、運載的物資種類、抵達二級倉庫點。

τ：二級車輛一次完整的運載任務，即 τ=（ci，wf，ej）（i=1，2，…，n；f=1，2，…，P；j=1，2，…，a）。二級車輛一次完整的運載任務為τ，它包括出發二級倉庫點、運載物資種類、抵達災害點。

Φ：一級序列完整的調度方案信息，即 Φ=｛φ1，φ2，…，φP｝，其中，φg（g=1，2，…，P）表示一級序列中第g個運輸工具的調度方案信息，包括一系列運載任務序列和該運輸工具的信息，φg=｛μ1，μ2，…，μχ；rk｝，即第g個運輸工具的調度方案信息為 φg，車輛信息為rk，有χ次運載任務序列。

Ω：二級調度方案，即 Ω=｛ω1，ω2，…，ωq｝，其中，ωg（h=1，2，…，q）表示二級序列中第 h個運輸工具的調度方案信息，包括一系列運載任務序列和該運輸工具的信息；ωh=｛τ1，τ2，…，τy；νf｝，即第 h個運輸工具的調度方案信息為 ωh，車輛信息為 νf，有y次運載任務序列。

T1：一級車輛調度時間集合，即 T1=｛t1φ1，

t1φ2，…，tφP｝。其中，t1φg（g=1，2…，P）表示第 g個運輸工具的調度完成時間。整個調度任務完成時間T1s=max（t1φg）。

T2：二級車輛調度時間集合，即 T2=｛t2ω1，t2ω2，…，t2ωq｝。其中，t2ωh（h=1，2，…，q）表示第 h個運輸工具的調度完成時間。整個調度任務完成時間T2s=max（t2ωh）。

目標函數：m in（max｛T1s，T2s｝）。

3 兩層調度算例

一級倉庫點分別為 b1，二級倉庫點分別為 c1，c2，c3，災害點分別為e1，e2，e3，e4，e5，3種應急物資w1，w2，w3，即分別對應為藥品、食品、生活用品。一級序列有2種車型，分別為大、小貨車，車輛編號分別為1～6，7～8，運載量分別為10 t和5 t，滿載速度分別為80 km/h和85 km/h。二級系統有2種車型，分別為大、小貨車，車輛編號分別為1～4，5～14，運載量分別為10 t和5 t，滿載速度分別為60 km/h和65 km/h。公路運輸路徑關系如圖1所示，一級高速公路運輸路徑距離（高速公路）如表1所示，二級高速公路運輸路徑距離（普通公路）如表2所示。3種應急物資在各倉庫點中的庫存量和在各災害點中的需求量如表3所示，其中，“∞”表示兩點間的道路不通。求解目標：以調度完成時間最短為目標，求解調度方案。

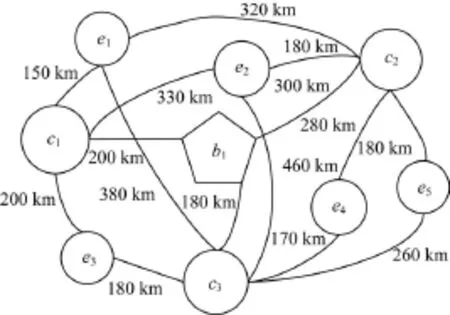
圖1 各倉庫、災害點的運輸路徑關系

表1 一級各倉庫、二級各倉庫的運輸路徑距離 km

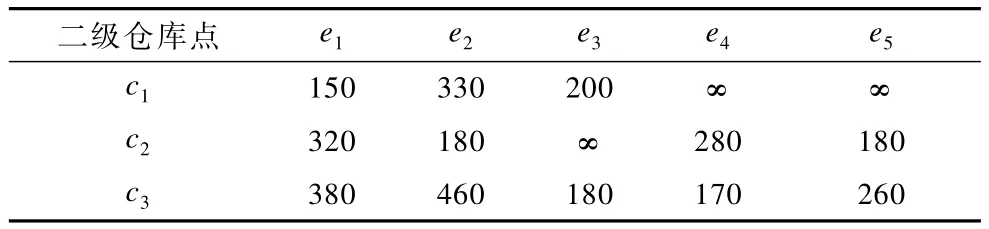
表2 二級各倉庫、災害點的運輸路徑距離 km

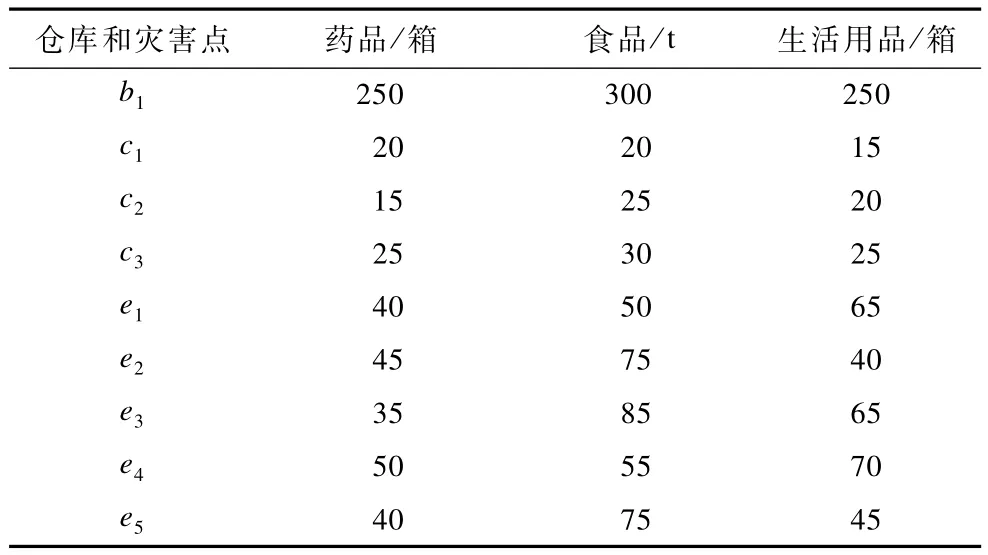
表3 各倉庫、災害點的存儲量與需求量

4 應用遺傳算法的算例求解過程

4.1 參數編碼

在一次應急物資調度中，參加調度任務的所有車輛的調度任務序列為一條染色體，其中任一輛車的全部調度任務為一個基因，任一輛車的部分調度任務定義為基因序列，任一輛車的單次完整調度任務為一個基因單元。

本文研究模型采用符號編碼方式，具體編碼符號定義如下：

b1代表一級倉庫點。

c1，c2，c3分別代表3個二級倉庫點。

e1，e2，e3，e4，e5分別表示5個災害點。

w1，w2，w3分別代表藥品、食品和生活用品。

r1，r2分別代表一級2種運輸工具：大貨車和小貨車，且r1=｛10，80，6｝，r2=｛5，85，2｝，即大貨車和小貨車的載重量分別為10 t和5 t，滿載速度分別為80 km/h和85 km/h。大小貨車按先大車后小車依次編號。

ν1，ν2分別代表二級2種運輸工具：大貨車和小貨車，且 ν1=｛10，60，4｝，ν2=｛5，65，10｝，即大貨車和小貨車的載重量分別為10 t和5 t，滿載速度分別為60 km/h和65 km/h。編號同一級。

μ=（bi，wf，cj）代表一級的基因序列單元，其中，bi代表一級倉庫點；wf代表運輸物資種類；cj代表目的二級倉庫點。

Φ=｛φ1，φ2，…，φP｝表示某個運輸工具在某次調度任務中的全部調度任務。

τ=（ci，wf，ej）表示二級的基因序列單元，其中，ci代表出發二級倉庫點；wf代表運輸物資種類；ej代表目的災害點。

Ω=｛ω1，ω2，…，ωq｝表示某個運輸工具在某次調度任務中的全部調度任務。

種群初始化即為按照設定的種群規模，生成相應數目的染色體。本文遺傳算法中種群規模為50。

本文將調度任務完成時間定為目標函數值。

4.2 遺傳算子

遺傳算子具體如下：

（1）基本遺傳算子

染色體間交叉操作和基因的變異操作實現遺傳算法的基礎功能。在獨立處理各級調度任務的遺傳算法中，染色體的雜交過程中采用多點一致雜交。多點一致雜交的具體雜交操作為：對2條父代染色體的每個相同基因位置上的基因序列依次進行雜交操作，即選取兩相同基因位置的基因序列的一共有的雜交點，互換雜交點后續的該基因位置的基因序列。

（2）輔助遺傳操作算子

根據供求關系約束條件，對遺傳變異產生的染色體進行處理，使各需求點的需求均滿足，使得一級倉庫點的各型物資出貨量不超過對應物資儲量。修復操可以分為：補給量大于需求量，補給量小于需求量，供給量大于存儲量。分別按照相應的處理方法進行修復。

計算遺傳算法生成的染色體所對應的調度方案中的每個物資需求點的對應補給量。逐個將各需求點的各型物資需求量與其補給量進行比較，若對某點某型物資補給量小于需求量，則在最先完成任務鏈的車增加一次運輸這種物資到該點的任務，重復此步驟至所有需求點對各類型物資需求均得到滿足。

若某點某型物資補給量過多，則在染色體中將含有到該點該型物資運輸任務的車中找到完成任務鏈耗時最長的那輛車，并刪除一次過量補給的任務，重復此步驟至各需求點對各型物資至補給均不過剩。

對于倉庫點修復處理則在染色體中搜索某物資出貨量大于實際儲量的倉庫，隨機將含有這些不合理的任務的車輛的轉貨點轉移到儲量富余的倉庫，重復此步驟至一級倉庫點對各型物資出貨量不超過其儲量。二級倉庫的物資出貨大于其儲量產生的缺口由一級調度系統來補充完成，因此計算二級調度的遺傳算法中無此修復操作。

本文將目標函數值的倒數定義為適應度值。若調度方案任務完成時間越短，則目標函數值越小，其適應度值越高。

4.3 分層獨立求解

本文算例二級倉庫有一定儲備保證二級車輛在二級倉庫不會有等待現象、一級調度任務時間相對二級調度任務時間較短。基于此，采用分層獨立求解方法。

本文應用遺傳算法先對二級調度系統進行求解得出在滿足二級災害點時的二級優秀調度方案，根據此方案得出二級倉庫的理論出貨量，進而判斷各二級倉庫的物資是否不足，根據二級倉庫的理論不足量再對一級調度系統進行遺傳算法求解得出補足二級倉庫的理論物資缺口的一級優秀調度方案。

詳細流程如下：首先初始化二級種群（50條染色體），對二級種群進行雜交、變異、修復操作生成新的50條二級染色體，經過自適應度評價的篩選得到較優的新的二級種群，再對新的一級種群進行雜交、變異、修復操作生成最新的50條一級染色體，如此重復上述過程，直到滿足終止條件，得到滿足各個二級倉庫點的需求二級染色體序列。通過分析滿足要求的二級染色體序列可以計算出各二級倉庫需要從一級倉庫需求的物資種類和數量，需要從一級倉庫補貨的二級倉庫即為一級調度系統的需求點，再用遺傳算法對一級調度系統進行同樣的操作即可得出一級調度方案。

5 算例求解分析

5.1 求解過程

本文將遺傳算法迭代過程中染色體的目標函數值即任務完成時間與迭代次數的關系數據進行保存并繪圖分析。當迭代至某級調度的任務完成時間穩定時，此時種群中的最優染色體所對應的調度方案即可對應得到該級的一個優秀調度方案。

（1）二級任務完成時間的收斂情況

基于遺傳算法求解一級序列并且在迭代50 000次基礎上，得到最優一級序列和二級倉庫獲得量，將二級倉庫獲得量與二級倉庫的原有存儲量作為二級序列現有存儲量，基于遺傳算法求解滿足要求的二級序列。

分析前50 000次迭代任務時間和迭代次數的關系數據簡單算出任務時間下降梯度，在完成50 000次迭代后得到最優二級序列的任務完成時間的收斂情況下，二級序列的調度任務完成時間（T2s）與迭代次數的關系分別如圖2和表4所示。

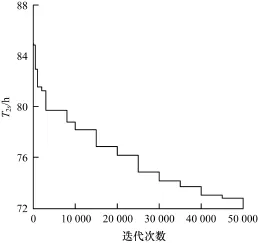
圖2 迭代50 000次后二級任務完成時間的收斂情況

表4 二級任務完成時間與迭代次數的關系1

由圖2可知，在50 000次迭代后，二級序列任務完成時間的收斂圖中能看到收斂比較明顯，但是數值沒有穩定。根據之前的數據預測任務時間穩定發生在200 000次以內，因此本文分析迭代200 000次的調度任務時間與迭代次數的關系，其二級序列調度任務完成時間與迭代次數的關系分別如圖3和表5所示。

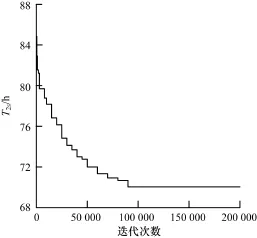
圖3 迭代200 000次后二級任務完成時間的收斂情況

表5 二級任務完成時間與迭代次數的關系2

由圖3可知，當將二級迭代200 000次時，可以看到數據有明顯收斂趨勢，迭代次數為90 000時任務完成時間已經穩定。由表5可知，當二級序列迭代次數達到50 000次以上，任務完成時間下降速度緩慢，當迭代次數到達 90 000次時，收斂值達到70.04 h。

（2）一級任務完成時間的收斂情況

本文將一級序列的迭代過程的循環終止條件設定為最大迭代次數50 000次，在完成50 000次迭代后得到一級序列任務完成時間的收斂情況下，一級序列的調度任務完成時間（T1s）與迭代次數的關系分別如圖4和表6所示。由圖4可知，當將一級序列終止條件定為迭代50 000次時，任務時間有明顯的收斂趨勢，因此將非聯動調度中的一級序列的循環終止條件設定為50 000次。由表6可知，當迭代至20 000次時，收斂值達到45.25 h。

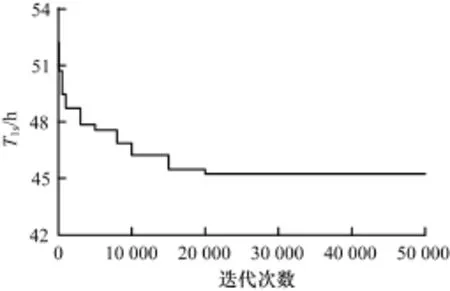
圖4 迭代50 000次后一級任務完成時間的收斂情況

表6 一級任務完成時間與迭代次數的關系

5.2 調度方案

由兩層調度任務完成時間穩定時對應的最優染色體可得最終調度方案，如表7和表8所示。其中，一級大貨車編號為1～6，小貨車編號為7～8；二級大貨車編號為1～4，小貨車編號為5～14。

表7 一級調度方案

表8 二級調度方案

5.3 結果分析

通過表7和表8可以看出，一級調度方案任務完成時間問 45.25 h，二級調度方案任務時間是70.04 h，通過對車輛各自運輸任務的運貨量計算和倉庫點物資的實時統計可得調度方案嚴格地符合供求條件，即一級倉庫各種物資的出貨量均不大于其實際存儲量，二級各倉庫的補給量與原有存儲量之和均不小于出貨量，各災害點的各種物資的補給量均嚴格滿足其實際需求量。同時每級調度方案中車輛各自任務時間相互偏差較小，調度合理。

6 結束語

本文以調度任務完成時間最短為目標，提出求解多種物資、多種車型的應急物資分層調度問題，并對此問題建立數學模型。從簡化問題的角度設計求解方法，通過設定符合實際情況的條件，使得串聯的調度系統間耦合程度降低，采用遺傳算法對各調度層進行依次獨立求解。設計一個典型算例進行程序設計并得出結果，通過結果分析可知約束條件均嚴格滿足且系統調度資源得到充分利用，分層獨立求解方法在滿足二級倉庫有一定儲備的情況下，求解步驟較簡潔，并可明顯提高求解速度。因此，本文求解方法對求解分層調度問題具備可行性。然而，本文求解方法無法從全局最優的角度求得不同條件下的調度結果，因此，如何應用整體聯動的求解方法對物資分層調度進行求解將是今后研究的方向。并且對本文求解方法進行擴充，將調度問題擴展至多階段調度，也是有待研究的內容。

［1］ Mladenovic N.基于單點搜索的元啟發式算法［M］.趙秋紅，肖依永，譯.北京：科學出版社，2013.

［2］ 張俊偉，王 勃，馬范援.多倉庫多配送點的物流配送算法［J］.計算機工程，2005，31（21）：192-194.

［3］ 廖良才，王 棟，周 峰.基于混合遺傳算法的物流配送車輛調度優化問題求解方法［J］.系統工程，2008，26（8）：27-32.

［4］ 陳子俠，葉慶泰.基于城市配送的單車線路算法研究［J］.計算機工程，2005，31（11）：32-34.

［5］ Wei Yi，Kumar A.Ant Colony Optimization for Disaster Relief Operations［J］.Transportation Research Part E，2007，43（6）：660-672.

［6］ Hindi K S，BastaT.Effieient Solution of a Multicommodity，Multi-modal Network Flow Model for Disaster Relief Operations［J］.Transportation Researchpart A，1996，30（3）：231-235.

［7］ Sheu Jiuh-Biing.Special Issue on Emergency Logistics Management Transportation Research Part E：Logistics and Transportation Review［J］.Transportation Research Part E，2005，41（5）：459-460.

［8］ Barbarosoglu G，Arda Y.A Two-stage Stochastic Programming Framework for Transportation Planning in Disaster Response［J］.Journal of the Operational Research Society，2004，55（1）：43-53.

［9］ Beradi P，Bruni M E.A Probabilistic Model Applied to Emergency Service Vehicles Location［J］.European Journal of Operational Research，2009，196（1）：323-331.

［10］ Barbarosoglu G，Arda Y.A Two-stage Stochastic Programming Framework for Transportation Planning in Distaster Response［J］.Journal of the Operational Research Society，2004，55（1）：43-53.

［11］ Ozdamar L，Ekinci E.Emergency Logistic Planning in Natural Disasters［J］.Annals of Operations Research，2004，129（1-4）：217-245.

［12］ 張 軍.計算智能［M］.北京：清華大學出版社，2009.

［13］ 徐 磊.基于遺傳算法的多目標優化問題的研究與應用［D］.長沙：中南大學，2007.

［14］ 徐宗本，張講社，鄭亞林.計算智能中的仿生學理論與算法［M］.北京：科學出版社，2003.

編輯 陸燕菲

Research on Hierarchical Scheduling of Emergency Supp lies Based on Genetic Algorithm

HU Feihu，TIAN Chaohui，LI Wei，HAN Xin

（Department of Industrial Automation，School of Electrical Engineering，Xi’an Jiaotong University，Xi’an 710049，China）

Aiming at the hierarchical scheduling problem of multi-vehicle and multi-supply，this paper proposes a hierarchical scheduling scheme.A two-layer scheduling example is demonstrated for the problem，and it decouples the tow-layer example into two single-layer problem s.Taking minimize system scheduling task completion time as the objective function，it uses the genetic algorithm to get the scheduling scheme which describes the specific type of carried cargo，the source and the destination for each type of vehicle in sequence.In this hierarchical scheduling scheme，the output in each warehouse is below its storage，the requirement quantity of supplies in each emergency point meets requirement by the real-time statistics in each warehouse and the calculation of carried cargo in each task.The solving process of this scheme is simple and fast.

emergency supplies scheduling；hierarchical scheduling；vehicle scheduling；genetic algorithm；objective function

胡飛虎，田朝暉，李 威，等.基于遺傳算法的應急物資分層調度研究［J］.計算機工程，2015，41（10）：53-58.

英文引用格式：Hu Feihu，Tian Chaohui，Li Wei，et al.Research on Hierarchical Scheduling of Emergency Supp lies Based on Genetic Algorithm［J］.Computer Engineering，2015，41（10）：53-58.

1000-3428（2015）10-0053-06

A

TP311.1

10.3969/j.issn.1000-3428.2015.10.011

國家自然科學基金資助項目（61174154）；中央高校基本科研業務費專項基金資助項目。

胡飛虎（1973-），男，副教授、博士生導師，主研方向：復雜網絡建模及優化調度，嵌入式智能控制系統；田朝暉、李 威、韓 鑫，碩士研究生。

2014-09-22

2014-11-15E-mail：2476008926@qq.com