局部信息下的裝備維修保障力量網絡演化模型*

韓震，盧昱，古平

(軍械工程學院 裝備指揮與管理系，河北 石家莊　050003)

?

局部信息下的裝備維修保障力量網絡演化模型*

韓震，盧昱，古平

(軍械工程學院 裝備指揮與管理系，河北 石家莊050003)

摘要：針對現(xiàn)實中僅已知裝備維修保障力量系統(tǒng)部分信息的狀況，借鑒復雜網絡思想，在對裝備維修保障力量活動進行網絡化抽象的基礎上，提出了一種局部信息下的裝備維修保障力量網絡演化模型。同時，以一種參數(shù)可以靈活設置的動態(tài)演化模型代替真實的裝備維修保障力量作為仿真對象進行研究分析，探討了3種不同選擇概率下隨仿真時間變化的各項網絡指標，這些指標值驗證了裝備維修保障力量網絡的無標度特征以及小世界特征。

關鍵詞：維修保障力量；復雜網絡；演化模型；局部信息

0引言

隨著感知與響應保障理念的出現(xiàn)，裝備維修保障的網絡型、時效性、適應性、分布性、協(xié)同性都面臨新的考驗與挑戰(zhàn)[1]，這客觀上要求裝備維修保障力量由傳統(tǒng)的層級式樹狀形逐漸向復雜網絡性過渡。復雜網絡作為一門新興的交叉學科[2]，其思想已在許多領域取得了良好的應用效果[3-6]，其網絡化理論也必將指導裝備維修保障力量快速、平穩(wěn)的發(fā)展。針對戰(zhàn)時敵方僅掌握我方裝備維修保障力量系統(tǒng)部分信息的狀況以及目前從復雜網絡的角度研究其演化過程較少，故本文從復雜網絡的角度出發(fā)，提出了構建局部信息下的裝備維修保障力量網絡演化模型。

1裝備維修保障力量系統(tǒng)分析

戰(zhàn)時裝備維修保障任務和保障環(huán)境多變且不確定[7]，給裝備保障活動帶來高度的復雜不確定性。這就從一定程度上迫使傳統(tǒng)的樹狀形裝備維修力量系統(tǒng)向網狀形裝備維修保障力量系統(tǒng)演變。

裝備維修保障力量系統(tǒng)是指由維修人員、維修設備、維修器材、維修設施以及維修資料等，按照結構上綜合集成、功能上相互聯(lián)系、性能上相互補充而構成的一個復雜系統(tǒng)。這也可以理解為是由眾多維修單元、維修指揮機構以及維修資源倉庫等維修保障力量實體以及實體之間錯綜復雜的關系共同構成的有機整體，這就使其與復雜網絡在形狀(網狀形)上、結構(節(jié)點與邊)上以及特性(節(jié)點眾多，關系復雜，功能進化)上都有許多相似之處。因此本文提出采用復雜網絡理論對維修保障力量系統(tǒng)進行研究，揭示戰(zhàn)時裝備維修保障力量演化特性，為裝備維修保障指揮員戰(zhàn)前制定保障方案提供輔助決策。

根據(jù)復雜網絡的描述方式，將裝備維修保障力量中的維修保障力量抽象為節(jié)點，維修保障力量之間的聯(lián)系抽象為邊，邊上流動著維修資源、維修人員以及維修信息等。根據(jù)信息戰(zhàn)爭對保障組織互聯(lián)互通(邊的無方向性)以及快速實施保障(邊上時間限制性)的要求，故本文中研究的是無向加權網絡。

2維修保障力量網絡的參數(shù)定義

(1) 度分布

節(jié)點度k(i)是指連接節(jié)點i的所有邊的數(shù)量，而度分布是指整個網絡中所有節(jié)點度的概率分布情況。

(2) 中心度與節(jié)點能力

中心度h(i)是刻畫節(jié)點i處于網絡中心的程度，其表示為[8-9]

(1)

式中：k(i)表示網絡中節(jié)點i的度；N-1表示最大可能的鄰節(jié)點數(shù)。

中心度并沒有考慮節(jié)點自身的特點與性質，也就不能客觀刻畫節(jié)點自身的能力[1]，故根據(jù)節(jié)點的能力強弱,本文引入了表節(jié)點i能力權重的指標μ(i)。

(3) 網絡路徑平均時間

在加權維修保障力量網絡中，節(jié)點i與節(jié)點j之間的最短距離可以用時間權重wij來度量，則網絡路徑平均時間可以表示為

(2)

式中：N為網絡的節(jié)點數(shù)量。

(4) 網絡聚類系數(shù)

網絡中節(jié)點i有k(i)條邊將它與其他節(jié)點直接相連，而這k(i)個節(jié)點之間實際存在相互連接的邊數(shù)為Ei，則節(jié)點i的聚類系數(shù)可定義為[10-11]

(3)

則整個網絡的聚類系數(shù)為

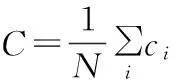
(4)

(5) 網絡巨組元節(jié)點數(shù)比率

網絡巨組元是指包含大多數(shù)節(jié)點的網絡局部區(qū)域。而巨組元節(jié)點數(shù)比率是指某個時刻前后巨組元中節(jié)點數(shù)的相對大小，反映的是網絡持續(xù)保持連通的能力，其表示為

(5)

式中：分母是指某個時刻前的m個巨組元中節(jié)點數(shù)之和，而分子則表示為同一時刻之后的m個巨組元中節(jié)點數(shù)之和。

(6) 網絡的質效

在加權網絡中，質效反映的是物質流、信息流以及能量流的流通準確程度。根據(jù)維修保障力量運行情況再結合質量熵的相關理論，定義加權維修保障力量網絡的質效R2為

(6)

網絡的巨組元節(jié)點數(shù)比率和質效從2個不同方向表現(xiàn)了網絡的效能。網絡的巨組元節(jié)點數(shù)比率持續(xù)偏高，即網絡的連通性越來越好，從網絡局部區(qū)域的節(jié)點數(shù)角度反映了網絡效能的提高；而網絡的質效增大，即網絡運轉越來越準確，則從網絡運轉精準角度反映了網絡效能的提高。

3局部信息條件下網絡的演化模型

網絡的演化模型主要有4種表現(xiàn)形式：實體(節(jié)點)的增/減，關系(邊)的增/減。目前多數(shù)文獻都對復雜網絡的演化模式做了大量研究[12-13]，其中主要包括蓄意攻擊以及隨機攻擊下的網絡演化模型。蓄意攻擊即敵方在掌握我方全面信息的情況下采取的攻擊方式；而隨機攻擊則是敵方在完全不掌握我方信息下所采取的攻擊方式。在現(xiàn)實戰(zhàn)場中，蓄意攻擊和隨機攻擊只是2種極端情況，更多的情況是局部信息下的攻擊方式[14-15]。

假設我方裝備維修保障力量網絡有N個節(jié)點，敵方獲取信息的概率為a(0≤a≤1)。當a=0時，即敵方不能獲取裝備維修保障網絡的任何信息，此時采取隨機攻擊方式。當a=1時，即敵方獲取了網絡的全部信息，此時采集蓄意攻擊方式。而更多的時候是a∈(0,1)，此時可將裝備維修保障網絡分為已知網絡區(qū)域(0,a](按照節(jié)點的重要程度的大小排序選擇性地攻擊該網絡區(qū)域)和未知網絡區(qū)域(a,1)(隨機攻擊該網絡區(qū)域)，這就是局部信息條件下的攻擊方式。

在信息化戰(zhàn)爭中，敵我雙方的較量除了打擊對方的作戰(zhàn)單元，更多的會摧毀對方的后勤保障單元，其中維修保障力量實體就是敵方重點打擊的對象之一。故戰(zhàn)時維修保障力量網絡，往往容易受到攻擊而造成網絡節(jié)點以及連邊的減少，而遭到損壞的維修保障力量實體為了保持其正常的維修保障能力，常常需要上級維修單位的支援，這就使得本級維修保障力量實體數(shù)量的增加，即增加網絡節(jié)點和邊。

敵方在獲取局部信息(即0

Step 1：初始維修保障力量網絡為一個有m0個節(jié)點以及e0條邊的無向加權網絡。

Step 2：敵方首先攻擊裝備維修保障力量網絡的已知區(qū)域。在每個相等的時間步長內，整個網絡按照一定的概率執(zhí)行以下4種不同情況中的一種。

情況1：敵方根據(jù)獲取的情報，有選擇地攻擊維修保障力量網絡，斷開ma條邊，其斷開的概率

(7)

式中:k(i)為節(jié)點i的度；wij為節(jié)點i與j之間的路徑時間。

情況2:以概率q2癱瘓nb個節(jié)點的保障職能，斷開所有與其相連的mc條邊，使其退出網絡，其被退出的概率

(8)

式中：h(i)為節(jié)點i的中心度；μ(i)為節(jié)點i的能力權重。

情況3：上級維修機構在接到申請支援時，以概率q3向已建立的網絡增加nd個節(jié)點vj(j=1,2,…,d)，并將新增加的節(jié)點配置在指定區(qū)域以及賦予相應的維修能力權重μ(i)(i=1,2,…,d)。每個新節(jié)點vj與已有節(jié)點vi建立me條邊。

(9)

情況4:向已建立的維修保障力量網絡增加mf條新邊，新邊的一端隨機選擇，另一端以概率q4進行選擇。

(10)

Step 3:敵方其次攻擊網絡的未知區(qū)域。在每個相等的時間步長內，網絡按照一定的概率執(zhí)行以下4種不同情況中的一種。

情況1:以概率p1刪除mk條邊，每條邊被刪除的概率為

(11)

式中:分母表示時間t時網絡的總邊數(shù)。

情況2:以概率p2刪除網絡中ng個節(jié)點，斷開所有與其相連的mh條邊。每個節(jié)點被選擇的概率為

(12)

式中：分母表示時間t時網絡的節(jié)點總數(shù)。

情況3:以概率p3增加nr個節(jié)點，并為新節(jié)點賦予不同的地理位置與節(jié)點能力μ(i)(i=1,2,…,k)，每個節(jié)點與網絡現(xiàn)有節(jié)點建立ms條邊。

(13)

情況4：以概率p4向已知網絡增加mu條邊。

(14)

4仿真實例

現(xiàn)以傳統(tǒng)的層級式樹狀型裝備維修保障力量網絡為例，說明其組織結構在局部信息條件下的演化過程，并采取數(shù)值仿真的方法來分析網絡演化模型的性能。

如圖1所示，將裝備維修保障力量組織環(huán)境下的各類實體抽象為節(jié)點，節(jié)點之間的聯(lián)系構成邊，節(jié)點的大小反映了各類維修力量實體的能力大小，邊上的數(shù)值反映了節(jié)點之間的路徑時間。根據(jù)上述對網絡指標參數(shù)的定義，采用Lingo軟件計算了圖1中的基本指標參數(shù)，結果如表1所示。

表1　維修保障力量網絡的指標參數(shù)

圖1　維修保障力量網絡的拓撲圖Fig.1　Topology of maintenance support force network

局部信息攻擊下的維修保障力量網絡，其已知區(qū)域內的蓄意攻擊由于我方維修保障力量具有一定的防偽能力，故概率不會是100%；而未知區(qū)域內的隨機攻擊由于敵方指揮員的指揮藝術以及攻擊裝備的智能化，故概率也不會太低。考慮以上因素，故本文設置了4種演化類型下的選擇概率范圍以及邊、點參數(shù)值，如表2所示。

表2　4種演化類型下的選擇概率以及邊、點參數(shù)值

設定網絡仿真時間設為100個時間步長，為了消除仿真過程中隨機因素產生的影響，對每一仿真過程都進行了10次獨立的仿真，再將結果取平均值。

5案例分析

仿真結束時對網絡節(jié)點的度分布進行統(tǒng)計，其結果如圖2所示。從圖中可看出3種不同選擇概率下的網絡度分布統(tǒng)計結果，其都逼近于曲線P(k)=k-a，a=2.3。故網絡節(jié)點的度分布基本服從a≈2.3的冪律分布，具有與電影演員網絡、生物代謝網絡以及自治層Internet等復雜網絡相近的無標度特征。

仿真過程中的網絡路徑平均時間如圖3所示。從圖3可以看出，3種情況下網絡路徑的平均時間先增加后減少，說明維修保障力量網絡隨著敵方從蓄意攻擊到隨機攻擊，經歷了減邊、減點速度從大于到小于加邊、加點速度。同時，可以看出隨著減邊、減點概率的增加，網絡路徑平均時間增加速度以及其極大值也隨之增加；隨著加邊、加點概率的增加，網絡路徑平均時間減少速度隨之增加，極小值隨之減少。仿真結束時網絡路徑平均時間小于初始值，故本文生成的網絡相對于傳統(tǒng)維修保障力量網絡保障速度上更快。

圖2　3種選擇概率下度分布統(tǒng)計結果Fig.2　Degree distribution statistics of three　　　different selection probabilities

圖3　仿真過程中的網絡路徑平均時間Fig.3　Average times of network path during　　　 the simulation process

如圖4所示，傳統(tǒng)維修保障力量網絡的聚類系數(shù)初始值為0。隨著仿真的進行，3種選擇概率下的網絡聚類系數(shù)維持在0附近，這是因為網絡的節(jié)點數(shù)與邊數(shù)總體處于減少狀態(tài)。而后網絡的聚類系數(shù)迅速增加，這是因為節(jié)點與邊的不斷加入，使得網絡變得越來復雜。最后網絡的聚類系數(shù)趨于穩(wěn)定，這時進入網絡的節(jié)點、邊與退出網絡的節(jié)點、邊數(shù)量上基本維持平衡。從圖中可知，隨著加邊、加點概率的增加，網絡聚類系數(shù)的增加速度也隨之增加，且聚類系數(shù)的極大值以及穩(wěn)態(tài)值也隨之增加。

圖4　仿真過程中網絡的聚類系數(shù)Fig.4　Network clustering coefficients during　　　the simulation process

從圖3可知維修保障力量網絡具有較短的路徑平均時間；而圖4可知網絡具有較大的聚類系數(shù)，故該網絡具有小世界特征。

仿真過程中的網絡巨組元節(jié)點數(shù)比率如圖5所示。圖5中，3種不同選擇概率下的網絡巨組元節(jié)點數(shù)比率開始一段時間內平穩(wěn)減少，這是因為大量的節(jié)點與邊不斷退出網絡。當仿真步長是55，選擇概率1(即q1=0.6時)的巨組元節(jié)點數(shù)比率值發(fā)生躍遷；當仿真步長是43，選擇概率2(即q2=0.7時)的巨組元節(jié)點數(shù)比率值發(fā)生躍遷；當仿真步長是38時，選擇概率3(即q3=0.8時)的巨組元節(jié)點數(shù)比率值發(fā)生躍遷。此時進入網絡中的節(jié)點數(shù)與邊數(shù)首次大于退出網絡的節(jié)點數(shù)與邊數(shù)。接著各自的網絡巨組元節(jié)點數(shù)比率值開始逐步減少，但其比率值都大于1，此時進入網絡的節(jié)點數(shù)與邊數(shù)大于退出網絡的節(jié)點數(shù)與邊數(shù)。最后3種選擇概率下的網絡巨組元節(jié)點數(shù)比率值在1附近波動，即此時進入網絡的節(jié)點數(shù)與邊數(shù)基本等于退出網絡的節(jié)點數(shù)與邊數(shù)，網絡的連通情況處于一種平穩(wěn)狀態(tài)。

圖5　仿真過程中的網絡巨組元節(jié)點數(shù)比率Fig.5　Ratio of the number of nodes of network giant　　　　component during the simulation process

仿真過程中的網絡質效如圖6所示。由于敵方的蓄意攻擊使得退出網絡的節(jié)點數(shù)與邊數(shù)大量增加，而隨著敵方隨機攻擊的到來，進入網絡的節(jié)點數(shù)與邊數(shù)逐漸超過撤出網絡的節(jié)點數(shù)與邊數(shù)。故從圖6可看出，網絡的質效剛開始處于減少狀態(tài)，當減少到一定程度時，其數(shù)值處于維持狀態(tài)，一定時間后網絡質效開始逐步增加(加邊、加點概率大，則其增加速率大，極大值也隨之增大)。

圖6　仿真過程中的網絡質效Fig.6　Network quality performances during　　　 the simulation process

從圖5，6可以看出，網絡的效能經歷了先逐步減小，達到一定程度后在其極小值附近波動，仿真一定時間后網絡的效能逐步增加，而后在一個穩(wěn)定的效能值附近波動。

由以上分析可知，隨著參數(shù)q1，q2,p1,p2的增大，網絡路徑平均時間的增加速率增加，網絡聚類系數(shù)的上升起點增加，巨組元節(jié)點數(shù)比率的減小速率增加，網絡質效處于降低狀態(tài)；而q3,q4,p3,p4的增大，則網絡路徑平均時間的極小值減小，網絡聚類系數(shù)穩(wěn)態(tài)值增加，巨組元節(jié)點數(shù)比率大于1的時刻提前，網絡質效的上升速率增加。故在對不同的維修保障力量建模時，可以根據(jù)維修保障力量內部運行的具體情況，結合實際網絡的特點，通過靈活的參數(shù)設置，得到更加真實的網絡演化模型。

6結束語

針對現(xiàn)實中經常面臨的僅已知裝備維修保障力量網絡中部分節(jié)點及連接關系，如何分析局部拓撲信息條件下網絡的演化規(guī)律將更具普適性，本文提出了一種基于局部信息條件下的網絡演化模型。它能夠通過參數(shù)調節(jié)揭示不同情況下的網絡演化規(guī)律，也能根據(jù)時間的變化實時顯示網絡的各項指標值。

參考文獻：

[1]徐玉國，邱靜，劉冠軍.基于多元加權網絡的裝備維修保障組織結構動態(tài)演化模型[J].兵工學報，2012,33(4)：488-496.

XU Yu-guo, QIU Jing, LIU Guan-jun. Dynamic Evolution Model of Equipment Maintenance Organizational Structure Based on Multielement-Weighted Network[J]. Acta Armamentarii, 2012,33(4)：488-496.

[2]方錦清，汪小帆，鄭志剛，等. 一門嶄新的交叉科學：網絡科學(上)[J]. 物理學進展，2007,27(3):239-343.

FANG Jin-qing, WANG Xiao-fan, ZHENG Zhi-gang, et al. New Interdisciplinary Science: Network Science(I)[J]. Progress in Physics, 2007,27(3):239-343.

[3]ATKINSON S R, MOFFAT J. The Agile Organization: From Informal Networks to Complex Effects and Agility[M]. Washington DC: DoD CCRP Puplication Series, 2005：5-27.

[4]FIEDICH F, GEHBAUER F, RICKERS U. Optimized Resource Allocation for Emergency Response After Earthquake Disasters[J]. Safety Science, 2005,2(35):41-57.

[5]LIN Y, DESOUZA K C, ROY S. Measuring Agility of Networked Organizational Structures via Network Entropy and Mutual Information[J]. Applied Mathematics and Computation, 2010,7(216):2824-2836.

[6]LI Wei, CAI Xue. Statistical Analysis of Airport Network of China[J]. Physical Review,2004,69(4):1539-1555.

[7]徐航，王維平，陳春良. 戰(zhàn)時裝備維修保障系統(tǒng)的狀態(tài)空間建模[J]. 系統(tǒng)仿真學報，2008,20(5):1139-1142.

XU Hang, WANG Wei-ping, CHEN Chun-liang. State Space Modeling of Materiel Maintenance Support System in Wartime[J]. Journal of System Simulation, 2008,20(5):1139-1142.

[8]BOCCALETTIA S, LATORAB V, MORENOD Y, et al. Complex Networks: Structure and Dynamics[J]. Physics Reports, 2006,424(1):175-308.

[9]ALBERT R, BARABASI A L. Statistical Mechanics of Complex Networks[J]. Reviews Modern Physics,2002,74(1):47-97.

[10]BOCCALETTI S, LATORA V. Complex Networks: Structure and Dynamics[J]. Physics Reports, 2006,424(4):175-197.

[11]何大韌，劉宗華，汪秉宏. 復雜系統(tǒng)與復雜網絡[M]. 北京：高等教育出版社，2010:127-130.

HE Da-ren, LIU Zong-hua, WANG Bing-hong. Complex Systems and Complex Networks[M]. Beijing: Higher Education Press, 2010: 127-130.

[12]ALBERT R, JEONG H, BARABASI A L. Error and Attack Tolerance of Complex Networks[J]. Nature, 2000,406(6794):378-382.

[13]COHEN R, EREZ K, BEN-AVRAHAM D, et al. Breakdown of the Internet Under Intentional Attack[J]. Physical Review Letters, 2001,86(16):3682-3685.

[14]陳盼，吳曉鋒，李怡，等. 局部信息條件下復雜網絡的攻擊策略[J]. 計算機應用研究，2010,27(12):4622-4623,4629.

CHEN Pan, WU Xiao-feng, LI Yi, et al. Attack Strategy for Uncertain Topology of Complex Networks[J]. Application Research of Computers, 2010,27(12):4622-4623,4629.

[15]吳俊，譚躍進，鄧宏鐘，等. 基于不等概率抽樣的不完全信息條件下復雜網絡抗毀性模型[J]. 系統(tǒng)工程理論與實踐，2010,30(7):1207-1217.

WU Jun, TAN Yue-jin, DENG Hong-zhong, et al. Model for Invulnerability of Complex Networks with Incomplete Information Based on Unequal Probability Sampling[J]. Systems Engineering-Theory & Practice, 2010,30(7):1207-1217.

Evolutionary Model of Equipment Maintenance Support Force Network with Partial Information

HAN Zhen，LU Yu，GU Ping

(Ordnance Engineering College,Equipment Command and Management Department，Hebei Shijiazhuang 050003，China)

Abstract:Aiming at the current situation that only partial information of equipment maintenance support force system is known, by referring to the idea of complex network and abstracting activity process of equipment maintenance support force into a complex network, an evolutionary model of equipment maintenance support force network with partial information is proposed. At the same time, by analyzing a dynamic evolution model parameters that can be flexibly set instead of the real equipment maintenance support force as an object of simulation to study, various network indicators of three different selection probabilities are discussed by following the simulation time. These index values prove that equipment maintenance support force network has scale-free and ‘small-world’ characteristics.

Key words:maintenance support force；complex network；evolutionary model；partial information

中圖分類號：E92；TP391

文獻標志碼：A

文章編號：1009-086X(2015)-01-0140-06

doi:10.3969/j.issn.1009-086x.2015.01.024

通信地址：050003石家莊市新華區(qū)和平西路97號軍械工程學院信息工程系E-mail：hanzhenzhen1986@163.com

作者簡介：韓震(1986-)，男，四川資陽人。博士生，主要研究方向為裝備保障信息化理論與應用。

基金項目：國家自然科學基金(61271152)

收稿日期：2013-10-25；
修回日期：2014-02-21