地球-火星之間的往返軌跡全局一體化優化設計

姬聰云 南 英 安 彬 陳昊翔

南京航空航天大學航天學院，南京210016

進入21世紀，以火星，小行星為牽引的探測計劃即將拉開序幕。火星是地球的近鄰，它的特征在很多方面都與地球極為相似，是太陽系八大行星之一，按離太陽由近及遠的次序排列為第4。火星對于人類有一種特殊的吸引力，因為它是太陽系中最近似地球的天體，它的赤道平面與公轉軌道平面交角非常接近于地球，這使它也有類似地球的四季交替，同時，火星的自轉周期為24小時37分，火星上的一天幾乎和地球上一樣長。

有人認為，火星的現在就是地球的未來。因而開展火星探測和研究，對于認識人類居住的地球環境，特別是認識地球的長期演化過程，具有十分重要的意義［1］。從1965年的“水手4號”探測器到2012年的“好奇號”火星探測器登陸火星，美國在火星探測方面已具有很強的優勢。而軌跡優化是星際往返問題(火星探測)中至關重要的一步，牽涉到飛行器各種功能的實現和指標任務的達成，NASA已經確定了把軌跡優化技術作為下一代多級重復使用航天器能否成功的一個關鍵技術［2］。

關于地球-火星往返軌跡優化的論文并不多見，由文獻［3-4］可以看出，這些論文都只對由地球到火星的單程飛行軌跡進行優化，而且性能指標也比較單一(飛行時間或者燃料消耗量)，但是在真實飛行環境下，必須考慮使飛行時間最短和燃料消耗量最少的控制條件。另外，隨著深空探測技術的日趨成熟，未來還要考慮探測器返回地球的軌跡優化。美國近四十年的實驗研究與實踐已積累了豐富的經驗，對未來的飛行器設計已經擁有較為具體的藍本;我國在本世紀初開始了火星探測的規劃，并已經實施。因此，本文以美國NASA火星探測器為飛行器模型，結合我國的航天任務需求，起飛地點等實際情況，采用一種組合優化算法對整個火星探測的飛行軌跡(包括從地球到火星的飛行軌跡和從火星返回地球的飛行軌跡)進行了全局一體化優化設計。該組合算法包括靜態參數和動態參數優化方法。靜態參數優化采用遺傳算法，動態參數優化采用原始自然算法。

1 問題描述

2015年4月1日至2017年4月1日，將火星探測器從地球發射，在盡可能短的時間內到達火星，在火星探測工作1至2年時間，然后返回地球。

航天器的初始質量m=1500kg，推進器比沖Isp=3000s，推進的速度方向可以任意設定，推進器的開關時間和次數沒有限制。

航天火星探測軌跡優化是一個多目標優化問題，優化目標主要有:1)在火星駐留時間最長;2)飛行過程中所耗的燃料最省;3)往返飛行時間最短。航天器深空探測任務中在火星周圍駐留的時間越長，能夠使航天器上的有效載荷工作時間最長，獲得更多的有用信息數據;航天器飛行過程中所消耗的燃料越少，所耗費的成本越少，航天器之后也能進行更多的其它探索任務;往返飛行時間短可以使航天器所獲得的數據盡快傳送到地面研究人員手中，盡可能縮短人類探索太空的時間。

但是，顯然以上3個優化目標并不能同時達到，需要優化設計一整套飛行程序，使得以下綜合性能指標式(4)～(10)達到最優［5-7］，即:

飛行器最大可用推力:TMax=0.2N;飛行器離開行星時的最大可用速度差:ΔVMax=1.21 km/s，在離開地球和火星時，飛行器加速需要消耗一定的燃料，本問題中不作考慮，由其它子系統提供;ΔVM，f與ΔVE，f分別是到達火星與地球時相對火星與地球的速度 限 制［8-9］，ΔVM，f，Max=4.0km/s，ΔVE，f，Max=11.0km/s。

由式(1)可得，要使性能指標最大，航天器與火星交會時的誤差(dr，dv)最小，航天器返回地球時的剩余質量mf最大，任務飛行時間t1最短，同時航天器留在火星探測的時間t2最長。

在J2000坐標系中，地球和火星繞太陽運行采用多體動力學運動微分方程:

2018年作為改革開放40周年，從青磚黛瓦到高樓大廈，從綠皮火車到高鐵飛機，在中國擁抱世界的這四十年間，讓中國各行業翻開新的篇章。作為一名工業媒體人， 更是感嘆我國從工業化水平低到世界制造大國，完成現代化工業的華麗轉身。在飛速發展的階段，總會有一些契機，來讓我們思考未來的方向。

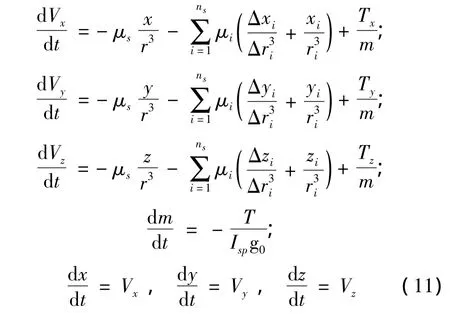
式中，(Vx，Vy，Vz)為探測器的飛行速度，(x，y，z)為探測器的3個直角坐標，(xi，yi，zi)為第 i顆行星的3 個直角坐標，(Δxi，Δyi，Δzi)為第 i顆行星與探測器的坐標值之差;r為探測器與太陽間的距離，Δri為飛行器與第i顆行星的距離;T(Tx，Ty，Tz)為探測器的控制推力，m為探測器的質量，Isp為發動機的比沖，g0=9.81m/s2;ns是所涉及到的行星個數，μs是太陽引力常數，μi是第i顆行星的引力常數。

2 軌跡優化方法

軌跡優化算法采用組合優化算法，優化算法的組合方式參見文獻［10-12］，關于組合優化算法優化程序中用到的靜態參數與動態參數優化算法分別是:1)靜態參數的迭代優化算法為改進遺傳算法，計算步驟參見文獻［13］;

2)動態參數的迭代優化算法為原始的自然算法［14］。

原始的自然算法的優化設計計算步驟共分N+1步，在文獻［14］的物質普適性算法基礎上進行簡化，與文獻［14］的計算步驟類同，具體的算法步驟如下:

第1步:計算t=t0～t1的軌跡，求從第0時段到第1時段最優控制u*(0)，從起點X(0)=X0出發，求第1時段最優控制u*(1)

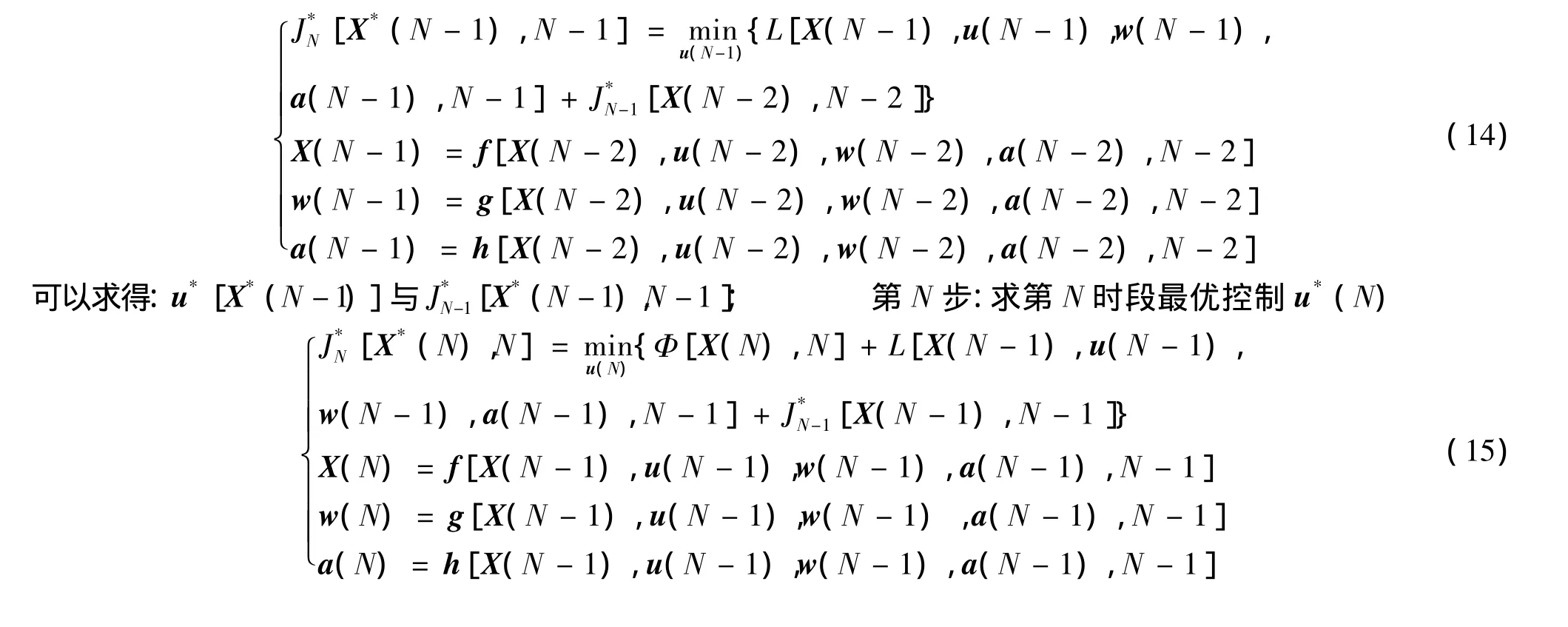
在自然計算的飛行仿真過程中，淘汰大量飛行方案，繼承進化了許多相對“優化”的方案，詳細的計算步驟與邏輯框圖參見文獻［14］。

3 仿真結果及分析

針對所提出的問題式(1)～(11)，采用飛行軌跡的組合優化算法，經過大規模的飛行優化數值仿真，得到一套最優的地-火往返飛行方案如下。

3.1 飛行仿真的結果

3.1.1 探測器從地球飛向火星

飛行器從地球出發到達火星的最優4-D飛行軌跡、速度—飛行時間、飛行器質量—飛行時間、推力控制—飛行時間分別見圖1～4。

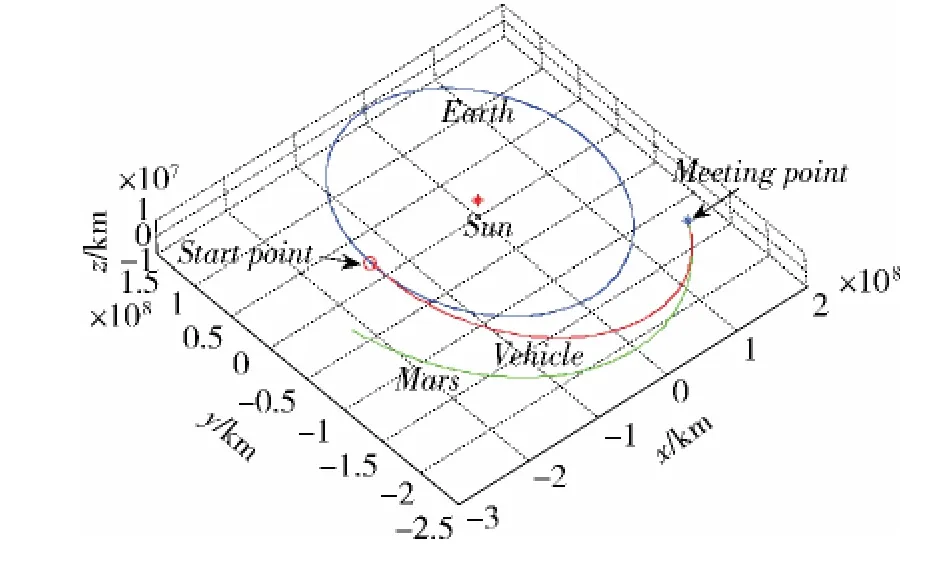
圖1 探測器從地球到火星的最優飛行軌跡

3.1.2 經過近500d在火星上的探測，探測器從火星返回地球

飛行器從火星返回地球的最優4-D飛行軌跡、速度—飛行時間、飛行器質量—飛行時間和推力控制—飛行時間分別見圖5～8。

3.2 仿真結果分析

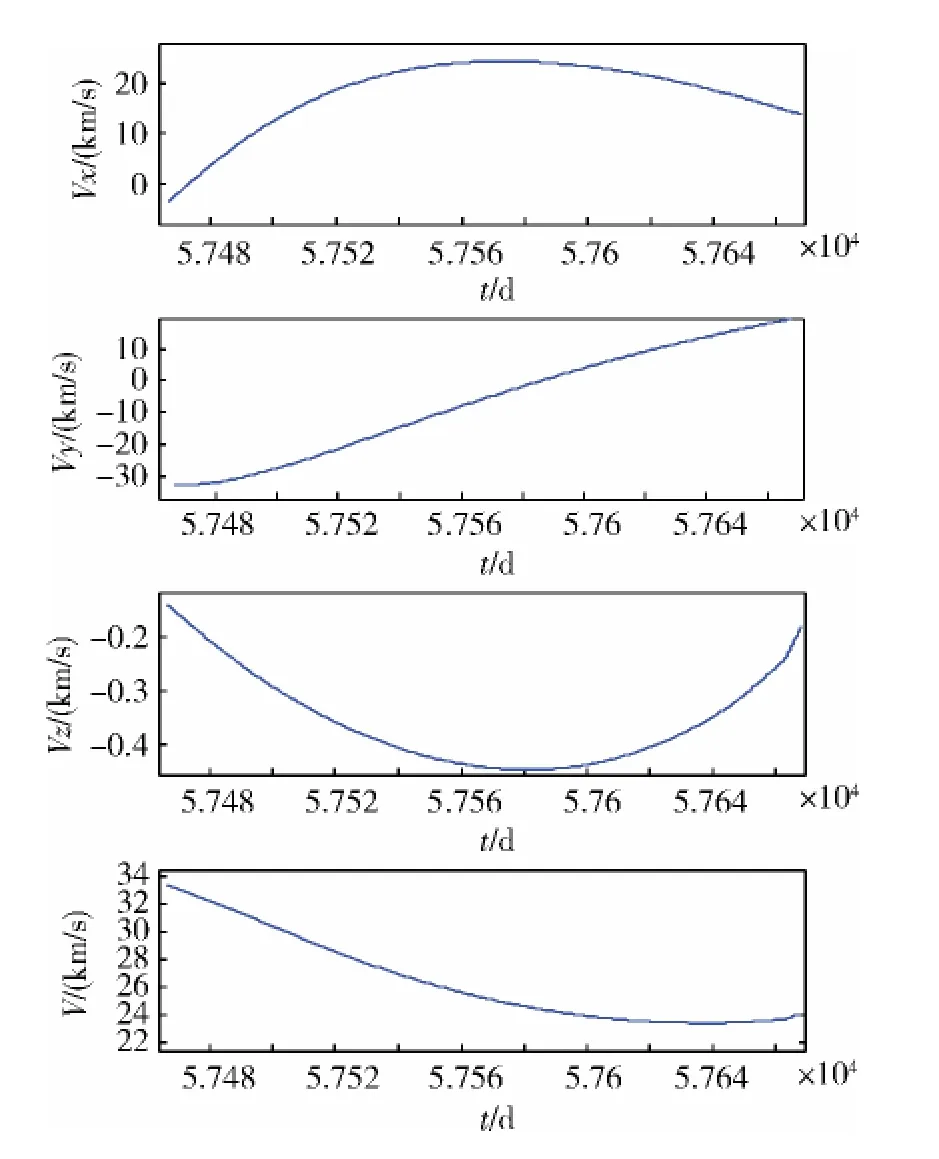
圖2 探測器出發后速度隨時間的變化

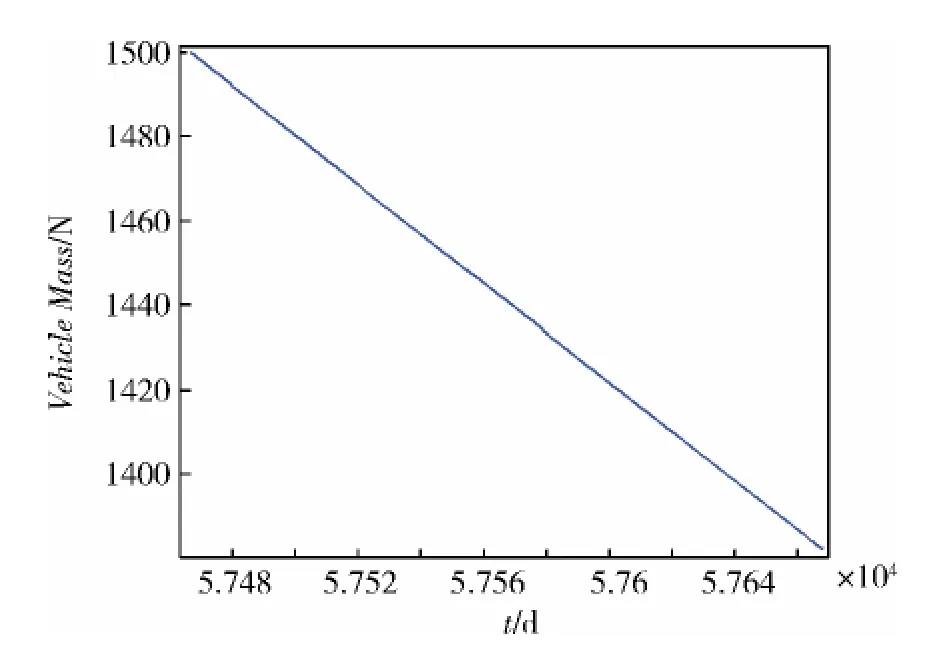
圖3 探測器出發后質量隨飛行時間的變化

經過大規模(靜態參數與動態參數組合優化的迭代)數值仿真，優選出一套最優飛行方案，該方案達到了在火星上探測時間的長度、往返的飛行時間、所耗發動機燃料的綜合性能指標最優，同時也滿足全部的約束條件。另外，由于多個性能指標是通過加權系數來綜合一體優化的，實際飛行任務中如果只需其中一個性能指標最優，就可設置其它性能指標的權系數為0。

1)由仿真結果可以得到詳細的飛行時間窗口

飛行器從地球飛往火星時所選擇的時間窗口與逃離速度，縮短了飛往火星的飛行時間;同時飛行器從火星返回地球時所選擇的時間窗口與逃離速度，也縮短了返回地球的飛行時間，并使總的往返飛行時間最短，全部往返飛行時間為

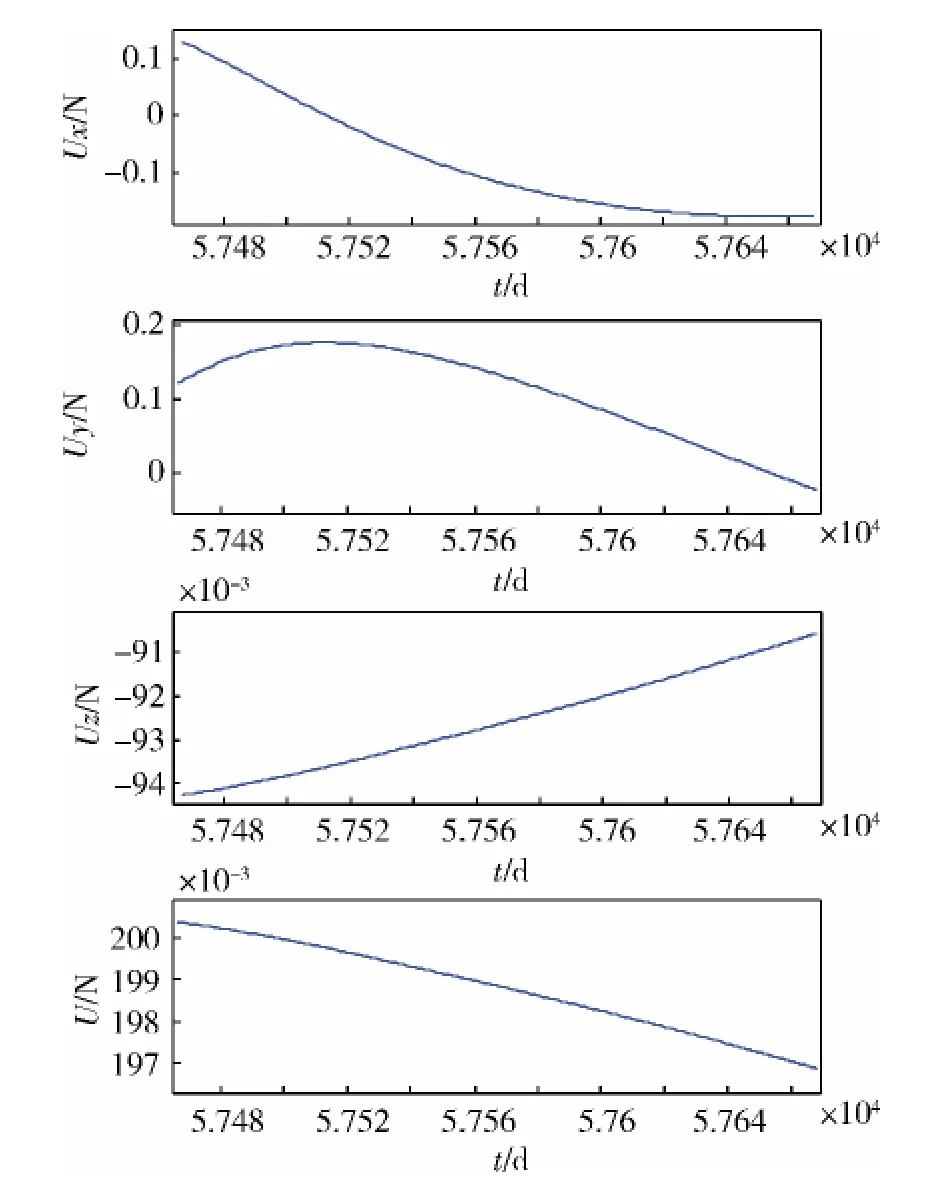
圖4 探測器出發后控制量隨時間的變化

圖5 探測器從火星到地球的最優飛行軌跡

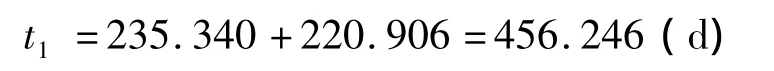
同時，以上時間窗口的選擇滿足了飛行器在火星上的探測時間，即飛行器在火星上探測時間為:

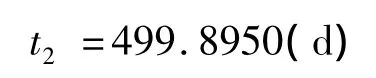
2)燃料消耗量也同時得到了最小化

從圖4和圖8可以看出，探測器在整個飛行任務中燃料消耗了850kg，包括地球飛往火星消耗的燃料和完成火星探測后返回地球飛行消耗的燃料。

3)滿足各種約束條件

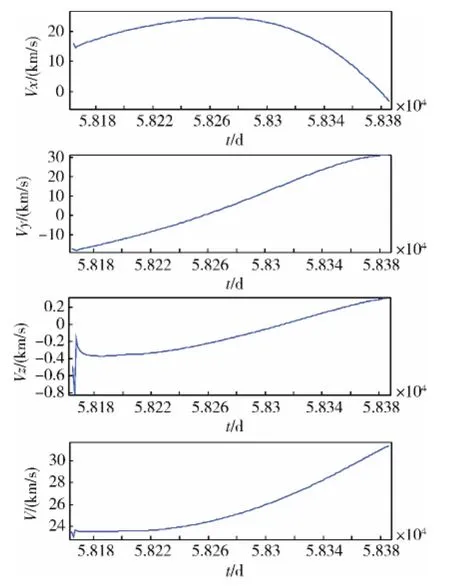
圖6 探測器返回時速度隨時間的變化

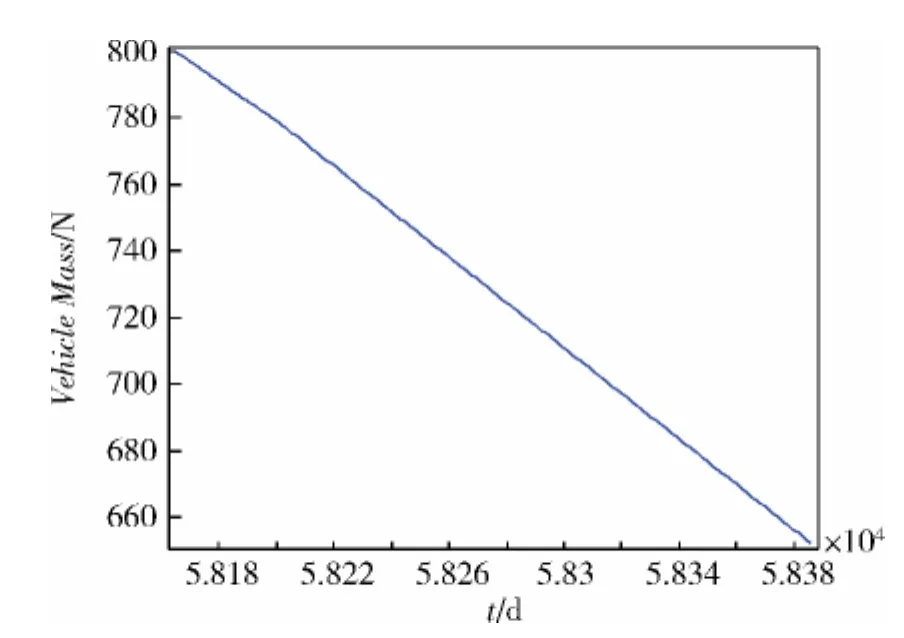
圖7 探測器返回時質量隨時間的變化

滿足控制變量約束:從圖4和圖8可以看出，整個飛行任務過程中控制變量u小于0.2N。

滿足飛行狀態的終端約束:探測器從地球出發飛往火星，到達火星(離火星球心距離4485km)時飛行器相對火星的速度為ΔVM，f=2.5km/s，即滿足ΔVM，f≤4.0km/s;探測器從火星返回地球，到達地球(離地心距離6491km)時飛行器相對地球的速度為 ΔVE，f=5.12km/s，即滿足 ΔVE，f≤ 11.0km/s。

4)隱含了借力飛行

從圖2與圖6可以看到，在飛行器靠近火星或地球時，飛行速度大小在增大，距離目標星的相對距離在減小，這隱含了飛行器借力飛行。

圖8 探測器返回時控制量隨時間的變化

4 結論

針對探測器在地球與火星之間往返飛行軌跡的全局一體化優化設計問題，采用一種航天器軌跡優化的組合算法，即靜態參數優化+動態優化相互迭代的數值優化算法。在滿足全部各種約束條件下，經過大規模的數值飛行仿真，得到了在地球與火星之間的全局一體的最優往返飛行軌跡，其中包括探測器分別離開地球與火星時的最優發射時間窗口與逃逸速度等。該飛行器沿著最優4-D軌跡飛行，可獲得最小的燃料消耗量，最短的往返飛行時間(即有限時間內在火星上探測時間最長);另外，飛行器在達到火星或地球時，分別達到行星的相對速度均滿足約束條件。這里指出，本文是基于多體動力學模型進行的軌跡優化，即隱含了借力飛行等因素，該飛行仿真結果具有實際的理論與工程價值，對未來我國火星探測飛行任務具有參考價值。

［1］ 張旭輝，劉竹生.火星探測無動力借力飛行軌道研究［J］.宇航學報，2008，26(9):1739-1746.(ZHANG Xuhui，LIU Zhusheng.Unpowered Swing by Flight Orbit Design for Mars Exploration ［J］.Journals of Astronautics，2008，26(9):1739-1746.)

［2］ Takeshi Tsuchiya，Takashige Mori.Optimal design of two-stage-to-orbit space planes with airbreathing engines［J］.AIAA，2005，42(1):90-97.

［3］ 尚海濱，崔祜濤，崔平遠，欒恩杰.地球到火星的燃料最省小推力轉移軌道［C］.中國宇航學會深空探測技術專業委員會第一屆學術會議，2005.1.

［4］ 尚海濱，崔平遠，欒恩杰.地球-火星的燃料最省小推力轉移軌道的設計與優化［J］.宇航學報，2006，27(6):1168-1173.(SHANG Haibin，CUI Pingyuan，LUAN Enjie.Design and Optimization of Earth-Mars Optimal-Fuel Low-Thrust Trajectory ［J］.Journals of Aeronautics，2006，27(6):1168-1173.)

［5］ 黃國強，南英，陸宇平.二級入軌空天飛機上升軌跡優化［J］.宇航學報，2010，31(3):641-647.(HUANG Guoqiang，NAN Ying，LU Yuping.The Ascent Trajectory Optimization of Two-stage-to-Orbit(TSTO)Space Plane［J］.Journal of Aeronautics，2010，31(3):641-647.)

［6］ Long Yaosong，Ye Zhengyin.Trajectory Global Optimization for Spacecraft Launched from the Earth in the Whole Solar System ［J］.Journal of Aeronautics，2012，33(2):160-166.

［7］ 黃國強，南英，陸宇平.小推力深空探測軌道全局優化設計［J］.航空學報，2010，31(7):1366-1372.(HUANG Guoqiang，NAN Ying，LU Yuping.Global Trajectory Optimization in Space Exploration by Lowthrust［J］.Acta Aeronautics et Astronautica Sinica.2010，31(7):1366-1372.)

［8］ 胡海龍，南英.有翼火星探測器進入軌跡優化設計［C］.第一屆進入減速與著陸全國學術會議，2013，7.

［9］ 南英，陸宇平，龔平.登月返回地球再入軌跡的優化設計［J］.宇航學報，2009，30(5):1842-1847.(NAN Ying，LU Yuping，GONG Ping.Optimal reentry trajectory design for mooncraft returning to the earth ［J］.Journal of Aeronautics，2009，30(5):1842-1847.)

［10］ 南英，陳士櫓，嚴輝.航天器軌跡優化的通用數值算法［J］.飛行力學，1996，14(3):20-25.(NAN Ying，CHEN Shilu，YAN Hui.A common numerical calculation method of optimizing the trajectories of space vehicles［J］.Flying Dynamics，1996，14(3):20-25.)

［11］ Huang Guoqiang，Lu Yuping，NanYing.A survey of numerical algorithms for trajectory optimization of flight vehicles［J］.Science in China Series E，2012，55(9):2538-2560.

［12］ NAN Ying，Hang Guoqiang，Lu Yuping，Gong Ping.Global 4-D Trajectory Optimization for Spacecraft［J］.Science China，2010，53(8):2097-2101.

［13］ 李鑫，南英，黃國強，華鵬，吳勝亮.改進遺傳算法的航空炸彈彈道反設計研究［J］.火力與指揮控制，2013，38(11):1960-1968.(LI Xin，NAN Ying，HUANG Guoqiang，HUA Peng，WU Shengliang.Reserve Design of Uncontrolled Bomb Trajectory Based on Improved Genetic Algorithm［J］.Fire Control＆ Command Control，2013，38(11):1960-1968.)

［14］ 南英，丁全心，陳哨東，黃國強，鄒杰.基于自然數值算法的眾多飛行器軌跡一體化全局優化設計［J］.中國科學，2013，43(6):636-659.(NAN Ying，DING Quanxin，CHEN Shaodong，HUANG Guoqiang，ZOU Jie.Global Optimal Design of Trajectories for Multiple Flight Vehicles Based on Natural Numerical Algorithm［J］.Science China，2013，43(6):636-659.)