一種基于線性近似的非線性系統模型預測控制方法*

蓋俊峰 趙國榮 周大旺

海軍航空工程學院，煙臺264001

模型預測控制(Model Predictive Control，MPC)是近年來崛起的一種成功的控制策略。MPC針對的是有優化需求的控制問題［1］，通過對某一性能指標的最優化來確定未來的控制作用［2］。由于現代工業生產過程的控制對象大多具有非線性特征，非線性系統的模型預測控制已成為當前的研究熱點。而非線性系統預測控制的關鍵問題在于如何處理非線性和降低在線計算量［1］。

非線性系統的設計和分析往往比線性系統困難得多，非線性微分方程通常不可能得到封閉形式的解析解，除非經過特殊處理，而傅里葉變換、拉普拉斯變換和疊加原理等適用于線性系統的強有力的數學工具都不再適用于非線性系統的控制問題。因此，對于實際工程操作人員來說，最簡單的方法就是把非線性動態特性線性化，然后再用成熟的線性系統設計方法完成對控制系統的分析和綜合［3］。

文獻［4］用中值定理將非線性系統進行線性化處理，用三次樣條函數來逼近線性系統的時變參數，并對樣條函數的常值參數進行了辨識;文獻［5］針對只含輸出非線性環節的系統沿期望的輸出軌跡用Taylor級數一階展開近似線性化，但是該方法不能處理含有輸入非線性環節的系統。運用Taylor級數展開法對非線性系統進行線性近似時，要求表征系統模型的輸入輸出函數必須連續可導，但有些物理系統并不滿足這一假設，因此Taylor級數展開法對此不再適用。文獻［6］指出，利用Stirling插值公式對非線性函數進行線性化處理的精度要高于Taylor一階近似，且不需對其進行求導運算，因此對不滿足連續可導假設的非線性系統，Stirling插值公式依然適用。

本文受文獻［6］的啟發，針對一類非線性系統(尤其是系統模型的輸入輸出函數不滿足連續可導條件的非線性系統)設計了一種基于線性近似的MPC方案。首先運用Stirling插值公式對非線性函數進行線性近似處理，并將模型預測控制性能指標重構為一個二次型最優化問題。最后，通過對二次型最優化問題的求解得到了模型預測控制的最優控制序列。為了減少計算量，忽略了線性近似過程中產生的非線性高階項。仿真結果表明，該方案能達到滿意的控制效果，且具有降低控制能量消耗和縮短控制時間的優點。

1 系統模型與問題描述

考慮如下的非線性離散系統:

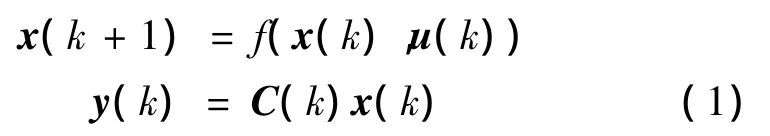
其中，x(k)∈Rn為狀態向量，u(k)∈Rm為控制輸入向量，y(k)∈Rp為輸出向量。f(·)為一連續的非線性函數，C(k)為一常數矩陣。

實際的工業過程中，受設備條件的限制，對系統的控制量和控制增量都有一定限制，需服從如下的約束條件:

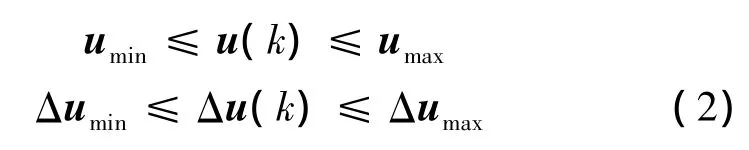
同時，為了避免系統輸出超過限制量，給出以下的輸出約束:

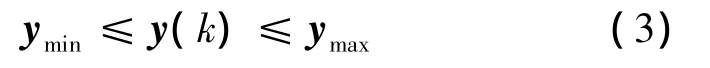
其中，umin≤umax，Δumin≤Δumax和ymin≤ymax分別為各向量的下界和上界。

模型預測控制是一種迭代最優化方法:在每個采樣時刻k，測量或估計當前狀態，然后通過對一個控制代價函數的最優化來獲得最優輸入向量。對模型(1)，給出以下滿足有限時域二次型規則的代價函數:

2 系統的線性近似

當非線性系統式(1)中的f(·)為一連續可微的非線性函數時，對于某些不太嚴重的非本質非線性特性，用Taylor近似方法進行分析和設計，在工作點的某一鄰域大體是正確的，產生的誤差也往往為工程上所接受。而當f(·)為一不可微的非線性函數時，由于不能對其進行求導運算，Taylor近似方法在此不再適用。區別于Taylor級數展開線性近似方法，用Stirling插值公式對非線性函數進行線性近似時無需進行求導運算，只需用有限線性運算來逼近該非線性函數［7-8］。由于Stirling插值公式能對余項直接進行控制，這使得在某些應用中其比Taylor近似更具吸引力。如果能選取合適的區間長度，可以確保Stirling余項能接近完整Taylor級數的高階項［9］。鑒于上述優點，本節采用Stirling插值公式法作為線性近似處理的數學工具。

下面用Stirling插值公式對非線性系統(1)進行線性近似。首先定義如下函數:

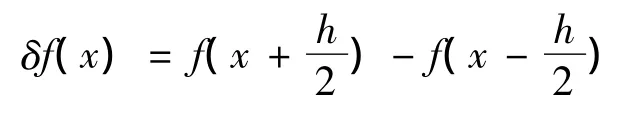
至此，當非線性函數f()·不可微時，非線性系統式(1)可以通過Stirling插值公式法線性近似為如式(13)的形式。這種形式可為構造二次型最優化問題提供方便，將在下節詳細說明。

3 二次型最優化問題的重構

此處，由于Q和R為正定陣，矩陣W也為正定陣，且所有的可行域都為凸的，因此最優化問題式(19)為一個凸二次規劃問題。對二次規劃問題式(19)求解，得到一個在控制域N上的控制增量向量Δˉu(k)，從而可計算出k時刻的最優控制輸入。

4 仿真分析

本節選取某非線性對象系統，其非線性函數f(·)不滿足連續可微條件，Taylor級數展開法不再適用于此處，故用Stirling插值公式法對其進行線性近似處理。所選非線性對象系統描述如下:

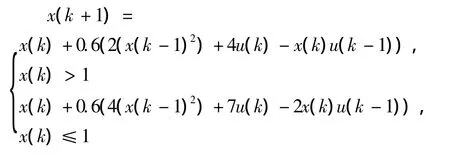
其中，預測域N=10，控制域Nu=3，控制時長為t=100s。權值矩陣Q=2.5I，R=0.5I。輸入約束為 -35≤u(k)≤35，控制增量約束為 -40≤Δu(k)≤40，輸出約束為-10≤y(k)≤10。本例的參考輸出軌跡設置為一個方波信號。

本例對直接基于原非線性模型的情況和基于近似線性模型的情況分別進行了仿真，結果如圖1～3所示。圖1中，Ref為參考輸出軌跡，y1為采用基于原非線性模型的MPC方案時系統的輸出軌跡，y2為采用基于本文近似線性模型的MPC方案時系統的輸出軌跡;圖2為2種不同情況下的控制輸入量曲線，其中u1為采用基于原非線性模型的MPC方案時的控制輸入，u2為采用基于本文近似線性模型的MPC方案時的控制輸入;圖3中，e1=y1-Ref，e2=y2-Ref，分別表示了采用2種MPC方案時的系統對參考輸出軌跡的跟蹤誤差。

仿真過程中，分別對2種方法進行100步優化計算所消耗的時間進行統計求均值，可得到2種方法平均每步優化計算所消耗的時間。

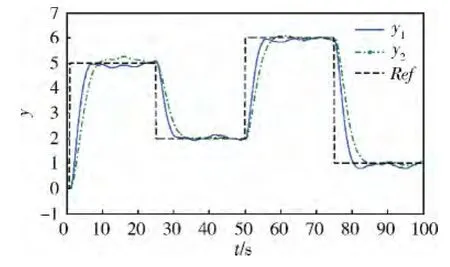
圖1 系統輸出跟蹤曲線

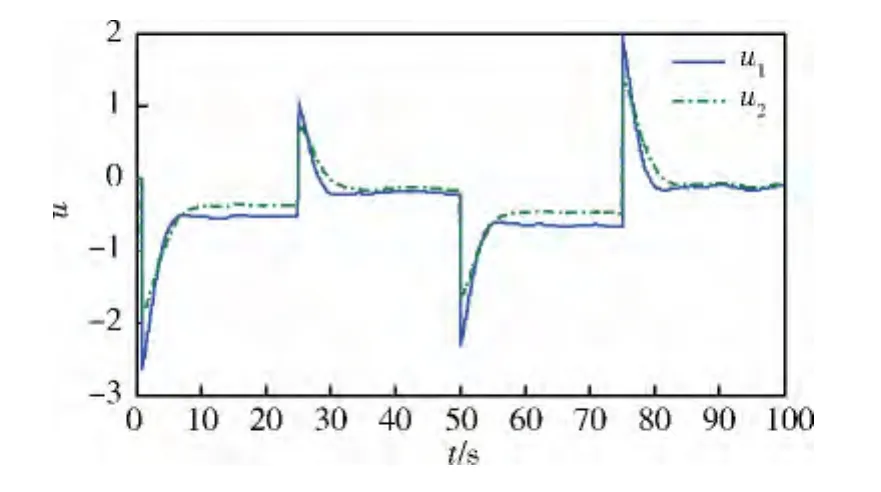
圖2 系統控制輸入曲線

經計算，直接基于原非線性模型的MPC方案消耗時間為0.04672s;基于本文近似線性模型的MPC方案消耗時間為0.01925s。

由仿真結果可以看出，本文提出的方案跟蹤精度要比直接基于原非線性模型MPC方案的跟蹤精度略低。其原因是在對非線性模型進行線性近似處理時，忽略了非線性高階項，這必然引入了線性化截斷誤差，使系統的跟蹤精度降低。但是，與直接基于原非線性模型的MPC方案相比，基于線性近似模型的MPC方案能減少控制能量的消耗，且大大節省了跟蹤時間。

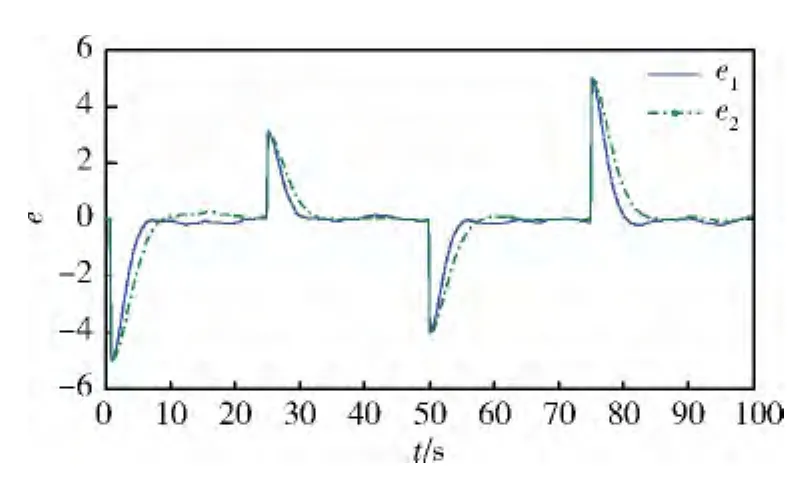
圖3 跟蹤誤差曲線

5 結論

提出了一種基于線性近似的非線性模型預測控制方法。首先運用Stirling插值公式對非線性函數進行線性近似處理，并將模型預測控制性能指標重構為一個二次型最優化問題。最后，通過對二次型最優化問題的求解得到了模型預測控制的最優控制序列。為了降低計算的復雜度，該MPC方案忽略了線性近似過程中產生的非線性高階項。仿真結果表明，本文的MPC方案能達到較滿意的次優控制效果，同時能降低控制能量的消耗，并且大幅縮短了控制時間。本文提出的方法僅為一種啟發性方法，在后續的工作中，需要對其穩定性等作進一步研究論證。

［1］ 席裕庚，李德偉，林姝.模型預測控制—現狀與挑戰［J］.自動化學報，2013，39(3):222-232.(Xi Yugeng，Li Dewei，Lin Shu.Model predictive control-Status and challenges［J］.Acta Automatica Sinica，2013，39(3):222-232.)

［2］ 席裕庚.預測控制［M］.北京:國防工業出版社，1993.(XI Yugeng.Predictive Control［M］.Beijing:National Defence Industry Press，1993.)

［3］ 胡躍明，胡終須，毛宗源，李志權.非線性控制系統的近似化方法［J］.控制理論與應用，2001，18(2):160-165.(Hu Yueming，Hu Zhongxu，Mao Zongyuan，Li Zhiquan.Approximation methods of nonlinear control systems［J］.Control Theory and Applications，2001，18(2):160-165.)

［4］ 郭健，陳慶偉，朱瑞軍.一類非線性系統的自適應預測控制［J］.控制理論與應用，2002，19(1):68-72.(Guo Jian，Chen Qingwei，Zhu Ruijun.Adaptive Predictive Control of a Class of Nonlinear System［J］.Control Theory and Applications，2002，19(1):68-72.)

［5］ Martin Rau，Dierk Schroder，Model predictive control with nonlinear state space models［C］.IEEE，AMC 2002-Maribor，Slovenia，2002，136～141.

［6］ 王亞鋒，孫富春，張友安，劉華平.一種跟蹤問題中的次優非線性預測控制算法［J］.控制與決策，2009，24(11)，1682-1686.(Wang Yafeng，Sun Fuchun，Zhang Youan，Liu Huaping.Suboptimal model predictive control for nonlinear system on tracking problem［J］.Control and Decision，2009，24(11):1682-1686.)

［7］ Magnus Norgaard，Niels K Poulsen and Ole Ravn［R］.Advances in Derivative-Free State Estimation for Nonlinear Systems，Technical report:IMM-REP-1998-15(revised edition)，Technical University of Denmark，Denmark，April 7，2000.

［8］ Schei T S.A finite difference method for linearization in nonlinear estimation algorithms［J］ .Automatica ，1997，33(11):2051-2058.

［9］ Magnus Norgaard，Niels K Poulsen and Ole Ravn.New developments in state estimation for nonlinear systems［J］.Automatica，2000，36(11):1627-1638.