中國園林的分形同構現象解析
陳晶晶,郭二輝,鄭曉軍,田朝陽
(河南農業大學林學院,河南鄭州 450002)
西方傳統設計的數學基礎是正方形、三角形、圓形等簡單規則形構成的歐幾里得幾何學,歐氏幾何被當作目前包括風景園林在內的幾乎所有設計學科的幾何基礎[1]。歐氏幾何形構圖理論,與其說是對自然界復雜形態理性的簡化、抽象,不如說是對自然界復雜性的否定,尤其是對大尺度的場地規劃采用歐氏幾何會對自然造成極大的破壞[2]。早在1889年,西方城市設計的先驅、奧地利建筑師卡米諾·西特[3]曾抨擊規則形用于城市設計是對藝術的扼殺,因為自然是所有藝術形式的源泉。對于根本不含簡單規則形的中國傳統園林,如用歐氏幾何的原理來解析,無異于用西方歌劇理論來詮釋中國的京劇。
以師法自然為特征的中國傳統園林有沒有幾何學基礎作為科學的依據呢?王庭蕙等[4-5]利用拓撲幾何學理論解讀了中國傳統園林中部分未知的幾何規律,為我們開啟了科學解讀傳統園林的榜樣。1975年,美籍法國數學家曼德勃羅編寫的《分形對象:形,機遇與維數》一書,使得人們對紛繁多樣的自然界形態有了新的認識,標志著分形理論的誕生[6],為師法自然的藝術設計提供了科學的幾何學基礎。
1 分形幾何理論
1.1 分形的概念
在自然界中,存在著許多傳統歐幾里得幾何學所不能描述的一大類復雜的、無規則的幾何現象,例如,蜿蜒曲折的海岸線、起伏不定的山脈、粗糙不堪的斷面、變幻無常的浮云、縱橫交錯的血管、令人眼花繚亂的滿天繁星等等,它們的特點是極不規則或極不光滑的[6],這就是分形幾何體。分形幾何學是一門以非規則幾何形態為研究對象的幾何學,由于不規則的現象在自然界中是普遍存在的,因此分形幾何學又被稱為大自然的幾何學。
1.2 分形幾何的基本特征
分形幾何體具有自然形體的“不規則形”和“局部與局部、局部與整體的相似性”2大基本特征。
1.3 分形幾何的應用
目前分形幾何在建筑設計、城市規劃、區域規劃、園林植物等許多領域都有廣泛的應用[7-11]。但是,在園林分析和設計中未見報道。
2 中國傳統園林中的分形同構現象
2.1 中國園林設計理論與分形理論
分形幾何理論的2大特征與中國傳統園林有著某種意義的契合。第一,中國傳統園林的設計手法是師法自然,即模擬自然要素的不規則形態。第二,中國傳統園林“移山縮水” “拳山勺水”,是對自然要素的科學的地理重構[12],即局部與整體的高度關聯和有機結合。
2.2 中國園林復合形的不規則特性
中國園林的復合形 (圖1),指由直線、曲線和折線組成的不規則形[2],是師法自然的產物,與自然界的分形幾何體極為一致,都是不規則的幾何形體。

圖1 中國傳統園林中的不規則復合形
2.3 中國園林復合形的自相似性
以古典園林諧趣園、退思園、獅子林、留園等眾多名園為例。
圖2-6可以看出,其各個園子的場地邊界、建筑群體邊界、水邊界、路徑的邊界存在自相似性,即分形同構現象。

圖2 諧趣園邊界、建筑群體布局內外邊界、路徑邊界、水系邊界的分形同構

圖3 退思園邊界、建筑群體布局內外邊界、路徑、水系的分形同構
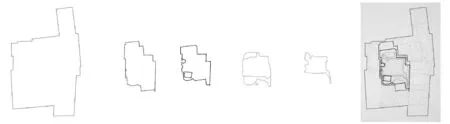
圖4 網師園邊界、建筑群體布局內外邊界、路徑、水系的分形同構
各個園子的各類要素形態,通過取形、微調、縮放、旋轉,達到與園址形態的分形相似。而園址的形態,是取形的基礎。各種園林要素的邊界形態,與園址的邊界形態具有極大的相似性,它們之間也存在相似性。
2.4 基于分形理論的中國園林構架
圖7為通過取形和縮放2種方法模擬的諧趣園建筑群體布局、路徑、水系邊界的分形圖,如果對
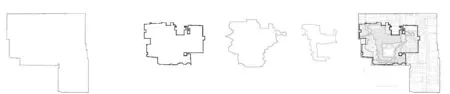
圖5 獅子林邊界、建筑群體布局邊界、路徑、水系的分形同構

圖6 留園中部邊界、建筑群體布局邊界、路徑、水系的分形同構
圖7 模擬諧趣園建筑群體布局邊界、路徑、水系的分形同構各要素的形態進一步微調 (理微)、旋轉 (互鎖、互含、向心),便可得到類似諧趣園的真實場景。
3 中國現代園林中的分形同構現象
中國傳統園林的現代化面臨諸多問題,最突出的問題是時代變遷下的尺度推移問題,即古典江南小尺度下的園林,如何在科學設計方法的指導下,適應大尺度公園、風景名勝區、各類城市綠地的設計。
分形幾何的“不規則形”和“局部與整體的相似性”2大基本原則,也許為解決這一問題提供了思路和方法。實際上,歷史上的大尺度皇家園林圓明園、頤和園、避暑山莊已經在無意識地使用分形幾何方法,實現了尺度的推移;中國現代大尺度園林中的佳作花港觀魚和方塔園、太子灣公園、紫竹院公園、陶然亭公園 (圖8-11)中也出現了大量不規則的分形幾何構形,其山、水、地形、邊界以及建筑布局都是運用分形幾何理論的結果。
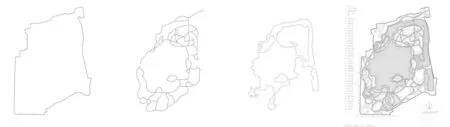
圖8 上海長風公園邊界、路徑、水系的分形同構

圖9 杭州花港觀魚公園的邊界、路徑、水系的分形同構

圖10 杭州太子灣公園的邊界、路徑、水系、建筑群體布局的分形同構

圖11 西安四盒園的邊界、路徑、園墻、建筑群體布局的分形同構
4 小結
西方園林界對自然的美學認可,始于17世紀;西方數學界對自然的科學認可,則遲至1975年分形幾何學創立時。中國傳統園林中對自然美的認知和對分形理論的無意識運用長達千年。如果說拓撲幾何中的太極圖是中國人世界觀、宇宙觀的圖示表達,那么,中國傳統園林中的分形意識是中國人自然觀的展示。中國園林的核心設計哲學依然是“尊重自然,師法自然”。相對于“機械”的歐氏幾何,“有機”的分形幾何理論和方法不僅可以承載這種設計哲學,而且有助于我們建立中國傳統園林的高級圖形語匯,構成理論并用于現代風景園林實踐。
[1] 郭湧.當下設計研究的方法論概述[J].風景園林,2011(2):68-71.
[2] 田朝陽,閆一冰,衛紅.基于線、形分析的中外園林空間解讀 [J].中國園林,2015,31(1):94-100.
[3] 卡米諾·西特.城市建設藝術[M].仲德崑,譯.南京:東南大學出版社,1990.
[4] 朱光亞.中國古典園林的拓撲關系[J].建筑學報,1988(8):33-36.
[5] 王庭蕙.中國園林的拓撲空間 [J].建筑學報,1999(11):60-63.
[6] 張濟忠.分形[M].北京:清華大學出版社,1995.
[7] 葉俊,陳秉釗.分形理論在城市研究中的應用[J].城市規劃匯刊,2001(4):38-42.
[8] 田達睿,周慶華.國內城市規劃結合分形理論的研究綜述及展望 [J].城市發展研究,2014,21(5):96-101.
[9] 冒亞龍,雷春濃.一種理性的建筑設計與評價視角:應用分形的建筑設計嘗試[J].重慶建筑大學學報,2005,27(4):4-9.
[10] 張霜霜.淺析論分形理論在建筑設計中的應用[J].四川建筑,2014(5):56-58.
[11] Jiang W,Ji C C,Zhu H.Fractal study on plant classification and identification [J].International Workshop on Chaos—Fractals Theories and Applications,2009:434-438.
[12] 董蒔.地理重構與情境剪輯: “空間地理”的意義構建[D].杭州:中國美術學院,2011.

