重頻結構大修改動力重分析的矩陣攝動法*
劉志軍, 王曉軍, 干為民
(常州工學院江蘇省數字化電化學加工重點建設實驗室 常州,213002)
?
重頻結構大修改動力重分析的矩陣攝動法*
劉志軍, 王曉軍, 干為民
(常州工學院江蘇省數字化電化學加工重點建設實驗室 常州,213002)
為拓展矩陣攝動法在結構重分析中的適用范圍,提高重分析計算精度,針對重頻結構參數大修改提出了重頻結構動力重分析的矩陣攝動法。采用高次增量法將反映重頻結構參數改變的質量矩陣和剛度矩陣的增量分別表示為小參數ε的一次與二次冪項之和,根據矩陣攝動理論推導得到重特征值的二階攝動解及相應特征向量的一階攝動解。數值算例表明,所提出方法極大提高了重頻結構大修改下的動力重分析計算精度。
重頻結構; 結構動力重分析; 結構大修改; 矩陣攝動法
引 言
在結構動態設計過程中,反復修改后結構的計算問題成為了主要困難,重分析方法能夠用來減少計算量,提高工作效率,受到了廣泛的重視和研究[1-6]。工程實際中常會有重頻率的退化系統,例如,飛機、宇航飛行器和海洋平臺等比較復雜的空間結構[7-10]。當結構具有重特征值時,已有的孤立特征值的矩陣攝動理論不能直接應用,而密集頻率結構振動分析的矩陣攝動問題往往是將密集模態處理成為重頻模態來進行研究[1,11],因此研究重頻結構大修改動力重分析的矩陣攝動法具有重要意義。
重特征值結構參數變化后,原來的一組重特征值可能分離為非重特征值,特征向量可能產生跳躍現象。確定重頻的特征向量的一階攝動需要用到二階攝動方程,如果重特征值的一階攝動量仍然是重的,就需要使用高階攝動方程才能確定特征向量的一階攝動量[1]。傳統經典矩陣攝動法將結構修改后的質量矩陣和剛度矩陣的增量分別表示為小參數ε的一次冪項形式,而重特征值的一階攝動解與小參數平方ε2對應的二階攝動方程相關,因此僅適用于結構的小修改重分析。當結構參數修改較大時,計算精度變差甚至變得沒有意義。筆者提出重頻結構大修改動力學重分析的矩陣攝動法,采用高次增量法將反映重頻結構參數改變的質量矩陣和剛度矩陣的增量分別表示為小參數ε的高次冪項之和,結構修改后的質量矩陣和剛度矩陣,與其特征值和特征向量一樣,同時進行高階攝動展開。根據矩陣攝動理論推導得到重頻特征值及特征向量的一階攝動解,極大提高了重頻結構大修改下的重分析計算精度。
1 重頻結構的改進矩陣攝動法
考慮結構振動特征值問題
其中:K0和M0為n×n的實對稱矩陣;Λ0為特征值對角陣;U0為n×n的模態矩陣。
設結構修改后的質量矩陣M、剛度矩陣K由下式表示
M=M0+εM1+ε2M2
(3)
K=K0+εK1+ε2K2
(4)
其中:εM1+ε2M2和εK1+ε2K2分別代表原系統的質量矩陣M0和剛度矩陣K0的變化;M1和M2分別為質量矩陣的一階攝動和二階攝動;K1和K2分別為剛度矩陣的一階攝動和二階攝動。
ε不必是小參數,與ε=0對應的系統稱為原系統。
當εM1+ε2M2→0和εK1+ε2K2→0時,M→M0,K→K0。
結構修改后相應的特征值問題為
(K0+εK1+ε2K2)U=(M0+εM1+ε2M2)UΛ
(5)
UT(M0+εM1+ε2M2)U=I
(6)
設原結構有一m重特征值λ0=λ01=λ02=…λ0m,其相應的特征向量為u01,u02,…,u0m,其余特征值為孤立特征值。u0j(j=1,2,…,m)的線性組合仍為該重特征值的特征向量,即
其中:αj為未知的待定系數。
攝動后的結構的重特征值和特征向量可表示為
Λm=Λ0+εΛ1+ε2Λ2
(11)
UADA)=U0mα+ε(U0mαCm+UACA)+ε2(U0mαDm+UADA)
(12)
其中:UA為n×(n-m)的矩陣,其中各列為除U0m之外的其他特征向量矩陣;Λm為m×m的攝動后的特征值對角陣;Λ1和Λ2為m×m的重特征值Λ0的一階和二階攝動對角陣;Cm,Dm和Em為m×m待定的展開系數矩陣;CA,DA和EA為(n-m)×m待定的展開系數矩陣。
將式(11,12)代入式(5,6),并用Um和Λm代替U和Λ,比較ε的同次冪系數,可得
ε2: (K0-λ0M0)(U0mαDm+UADA)+(K1-λ0M1)×(U0mαCm+UACA)+(K2-λ0M2)U0mα=M0U0m×α(CmΛ1+Λ2)+M0UACAΛ1+M1U0mαΛ1
(17)
方程(13)~(17)就是確定Λ1,U1,Λ2和α的基本方程。
1.1 特征值一階攝動Λ1的確定
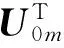
Wα=αΛ1
(18)
其中
(19)
求解特征值問題(18)可得到Λ1和α。
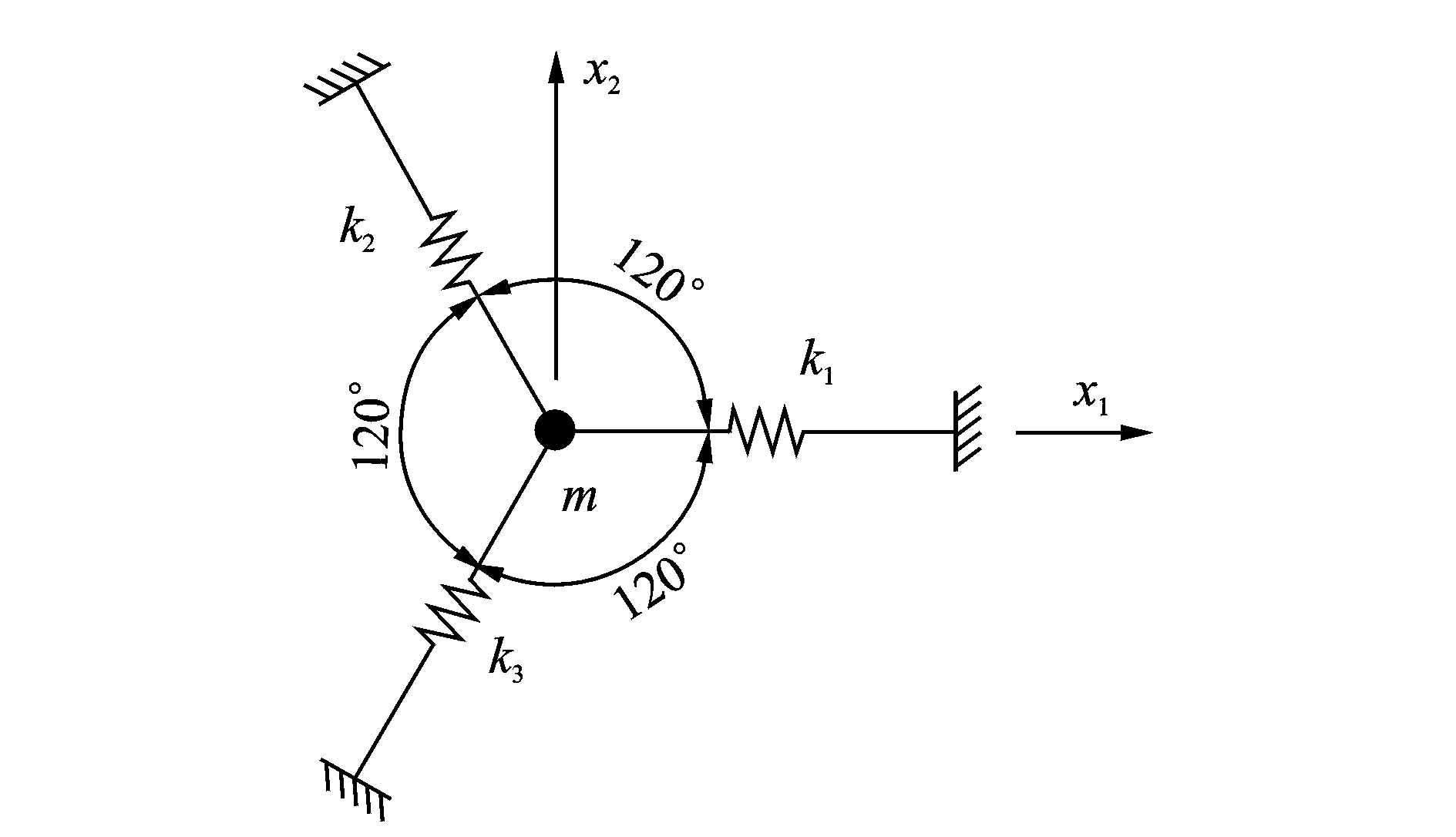
如果矩陣W無重特征值,則α可唯一確定;如果W有重特征值,就要補充高階攝動方程才能確定α。矩陣W無重特征值時有λ1i≠λ1j(i≠j),其中,λ1k(0 1.2 特征向量一階攝動U1的確定 特征向量一階攝動U1為 U1=U0mαCm+UACA (20) (21) (22) 由于矩陣CmΛ1-Λ1Cm的對角元素為零,而Λ2的非對角元素為零,故可求出 Λ2=diag(R11,R22,…,Rmm) (23) (24) 由式(16)可得 (25) 其中 (26) 由式(25)可知 (27) 如圖1所示的一個二自由度的系統,由3個彈簧支承的質點m在x1x2平面內微幅振動,取質點質量m=1 kg,當3個彈簧的剛度系數相同,取k1=k2=k3=1 N/m,這時該二自由度系統的兩個特征值相等,即λ1=λ2=1.5,相應特征向量u1=[1 0]T,u2=[0 1]T。 為了研究當結構參數改變時本研究方法的計算精度,假設質點質量的改變量從10%增加到60%,而第3個彈簧剛度改變量從-10%減少到-60%。與式(3,4)相應的攝動質量矩陣和剛度矩陣分別為 圖1 二自由度彈簧質點系統Fig.1 Mass-spring system with 2 degrees of freedom 將筆者提出的方法與文獻[1]中的重頻結構經典攝動解進行比較,定義固有頻率相對誤差err=(|ω-ωa|/ωa)×100%,其中:ωa為結構修改后的精確固有頻率;ω為用重分析方法計算得到的結構修改后的固有頻率。表1列舉了1,2階固有頻率的計算結果。 從表1中的數值結果可以看出,無論重頻結構參數改變多少, 按筆者攝動分析方法給出的重分析結果遠遠好于按重特征值經典攝動法給出的結果。 例如,當質點質量增加20%而第3個彈簧的剛度系數減少20%時,按筆者攝動分析方法給出的第1階特征值和第2階特征值的重分析相對誤差分別為0.054 2%和0.028 2%,而按重特征值經典攝動法給出的第1階特征值和第2階特征值的重分析相對誤差分別為1.538 5%和0.800 0%。隨著重頻結構參數改變增大,兩種方法計算誤差均有所增大;當重頻結構參數改變30%時,采用重特征值經典攝動法計算得到的兩階固有頻率的最大相對誤差超過5.6%,而筆者方法在重頻結構參數改變40%時計算得到的兩階固有頻率的最大相對誤差不超過0.3%,相同計算精度要求下,筆者方法的適用范圍更廣;當重頻結構參數改變量超過30%以后,經典攝動法的重分析計算結果誤差急劇增大,因此重特征值經典二階攝動法的適用范圍是重頻結構參數改變量在30%之內,而筆者方法在重頻結構參數改變60%時重分析計算得到的兩階固有頻率的最大相對誤差也未超過3.8%,因此筆者方法的適用范圍更廣,適用于重頻結構大修改情況。 表1 固有頻率比較 筆者提出了一種應用高次增量法來提高攝動解的精度并擴大其適用范圍的重頻結構動力重分析方法,該方法保留了經典攝動法簡單易行的特點,比文獻[1]中的經典方法只增加了少許的計算量,但計算精度和效率卻有了很大的提高。數值算例結果表明,筆者提出的方法具有很高的重分析精度,能夠用來解決重頻結構大修改情況下的近似重分析問題。 [1] Chen Suhuan. Matrix perturbation theory in structural dynamic designs[M]. Beijing, China: Science Press, 2007:97-131. [2] 倪衛明,王文亮.具有重特征值的弱阻尼系統的攝動法[J].復旦學報:自然科學版,1995,34(1):69-77. Ni Weiming, Wang Wenliang. A perturbation method for weakly damped systems with repeated eigenvalues[J]. Journal of Fudan University: Natural Science, 1995,34(1):69-77. (in Chinese) [3] 陳塑寰.退化系統振動分析的矩陣攝動法[J].吉林工業大學學報,1981,11(4):11-18. Chen Suhuan. Matrix perturbation for vibration analysis of degenerate systems[J]. Chinese Journal of Jilin University of Technology, 1981,11(4):11-18. (in Chinese) [4] 王文亮,胡海昌.重特征值的小參數法[J].復旦學報:自然科學版,1993,32(2):168-176. Wang Wenliang, Hu Haichang. Small parameter technique with repeated eigenvalues[J]. Journal of Fudan University: Natural Science, 1993,32(2):168-176. (in Chinese) [5] Hou G J W, Kenny S P. Eigenvalue and eigenvector approximate analysis for repeated eigenvalue problems[J]. AIAA Journal, 1992,30(9):2317-2324. [6] Choi K M, Cho S W, Ko M G, et al. Higher order eigensensitivity analysis of damped systems with repeated eigenvalues[J]. Computers & Structures, 2004,82(1):63-69. [7] 劉保國,殷學綱,韓國明,等.一維結構系統重頻特征問題的攝動傳遞矩陣法[J].機械強度,2002,24(3):335-338. Liu Baoguo, Yin Xuegang, Han Guoming, et al. Perturbation transfer matrix method for one-dimensional structural system with repeated eigenvalues[J]. Journal of Mechanical Strength, 2002,24(3):335-338. (in Chinese) [8] 張家濱,陳國平.基于子空間算法的對稱結構重頻模態識別[J].南京航空航天大學學報,2012,44(2):191-197. Zhang Jiabin, Chen Guoping. Modal identification of symmetrical structure with repeated frequencies based on subspace method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012,44(2):191-197. (in Chinese) [9] 劉福林,閆維明,何浩祥.重頻結構的振型識別及處理方法[J].工業建筑,2011,41(S1):368-372. Liu Fulin, Yan Weiming, He Haoxiang. Mode shape identification and disposal in the structure of overlap frequencies[J]. Industrial Construction, 2011,41(S1):368-372. (in Chinese) [10]于瀾,張文丹,付向南.非對稱重頻阻尼系統狀態向量的攝動分析[J].長春理工大學學報:自然科學版,2011,34(3):170-172. Yu Lan, Zhang Wendan, Fu Xiangnan. Rapid algorithm for gradients of state vectors in asymmetric damping system with repeated eigenvalues[J]. Journal of Changchun University of Science and Technology:Natural Science Edition, 2011,34(3):170-172. (in Chinese) [11]劉中生,陳塑寰.頻率集聚時模態分析的移位攝動法[J].宇航學報,1993,14(1):81-88. Liu Zhongsheng, Chen Suhuan. Perturbation analysis of vibration modes with close eigenvalues by eigenvalue shift[J]. Journal of Astronautics, 1993,14(1):81-88. (in Chinese) 10.16450/j.cnki.issn.1004-6801.2015.05.005 *國家重點基礎研究發展計劃(“九七三”計劃)資助項目(2010CB736104);常州工學院自然科學基金資助項目(YN1407) 2013-07-29; 2013-09-25 O302 劉志軍,男,1976年4月生,博士后、副教授。主要研究方向為結構動力學分析與優化設計。曾發表《索力振動測量的傳遞矩陣法》(《振動與沖擊》2011年第30卷第10期)等論文。 E-mail:uliuzj@163.com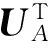
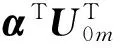
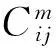
2 數值算例
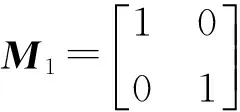

3 結束語


