基于結構光投影的薄膜振動模式分析

馮 偉，張啟燦

(四川大學電子信息學院光電系，成都610064)

引 言

薄膜是工業生產和自然生活中普遍應用的一類彈性元件，對薄膜振動測量的研究一直以來都受到人們的廣泛關注和重視。常見的振動測量方法主要有散斑法、圖像處理法、結構光3維傳感法等，不同的測量方法都有各自的優勢和應用范圍。

散斑法振動測量又分為電子散斑干涉測振［1］、數字散斑干涉測振［2］、相移數字散斑干涉測振［3］、雙精度數字散斑干涉測振［4］等。1971年由BUTTERS和LEENDERTZ提出的電子散斑干涉測振技術［5］，具有全場、非接觸、實時測量等優點。

WANG等人利用數字圖像處理和傅里葉變換的方法［6］，對一幅高頻振動模糊圖像經過一系列的變換和處理得到對應的振幅和振動方向信息，可以實現平面內任意方向振動的測量，振幅的測量精度可以達到亞像素級，很適合微小振動的測量。

基于結構光3維傳感的光學測量方法，以其全場、快速、非接觸、裝置簡單等優點，已經得到了廣泛的應用。其中ZHANG［7-8］等人利用結構光3維傳感技術，采用高幀頻CCD拍攝在外力作用下的鼓膜振動，得到整個鼓膜表面在振動過程中不同時刻的3維面形，再現了振動過程中的模式變換，同時得到了鼓膜振動的頻率和振幅等一些特征參量，但是此類高幀頻CCD價格昂貴。

作者在ZHAI［9］等人的研究基礎上，結合結構光3維傳感技術和時間平均法［10-11］的諸多優點，利用結構光投影和傅里葉條紋分析方法［12］來重建薄膜振動模式。同時使用高幀頻CCD對振動中的薄膜3維面形進行了測量重建，印證了振動模式的正確性。此外，本文中還將實驗檢測得到的振動模式與理論計算對應結果做了比較，證實了所提出方法的有效性。

1 條紋投影時間平均法原理

1．1 測量系統

振動物體測量的光路如圖1所示，虛線表示薄膜表面的振動情況。其中，E1和E2分別為投影系統的入瞳和出瞳，E3和E4為成像系統的入瞳和出瞳，L表示成像系統入瞳E3到參考平面的距離，d表示投影系統出瞳E2和成像系統入瞳E3之間的距離。

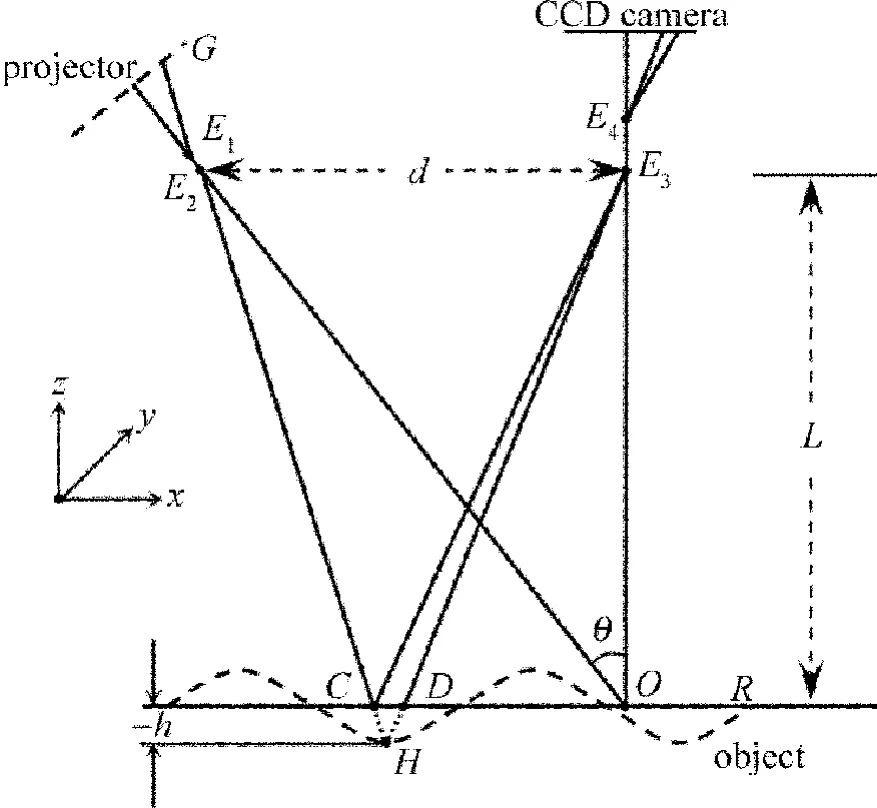
Fig.1 Optical path of system

1．2 原理分析

投影正弦條紋到振動薄膜上，在CCD的曝光時間T內，受到正弦激勵時薄膜表面變形條紋的平均光強

式中，a(x，y)，b(x，y)分別為薄膜振動狀態下的背景光場和非均勻反射率分布，f0是正弦調制光柵的空間載頻，λ =1/(f0tanθ)為等效波長，φ0(x，y)為薄膜靜止狀態時表面的相位分布，A(x，y)為振幅，J0為0階Bessel函數。對(1)式中變形條紋 ˉg(x，y，T)做傅里葉變換，可以得到條紋對應的傅里葉頻譜，選擇合適的濾波窗進行濾波，進行頻譜移中后，做逆傅里葉變換可以求得對應的復分布為:

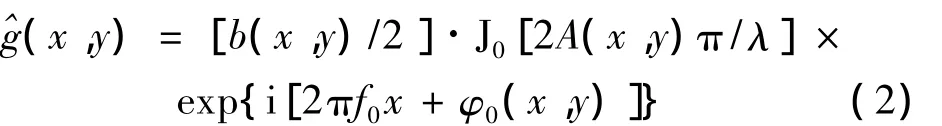
在薄膜振動幅度很小的情況下，薄膜表面的非均勻反射率b(x，y)是不變的。以同樣的步驟處理參考條紋，得到對應的復分布為:

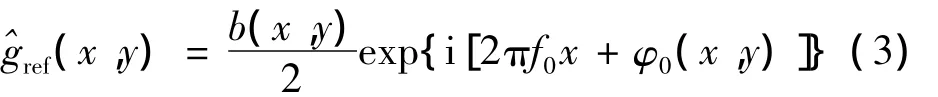
對(2)、(3)兩式取模后相除，得出振動薄膜表面強度比值分布為:

本文中通過計算機模擬和實際實驗來分析強度比值分布I(x，y)的變化趨勢和相對應的3維面形結果。

2 計算機模擬

模擬受正弦激勵的圓形薄膜，同時投影每個周期為12個像素的正弦條紋，CCD幀頻設為25frames/s。理想情況下，圓膜的振動方程可以表示為:

式中，umn(r，θ，t)是t時刻振動薄膜的位移，此時把薄膜的表面強度比值分布表示為(m，n)模式。c是圓形薄膜的半徑，，其中F為薄膜的表面張力，σ為薄膜的面密度，Zmn是n階Bessel函數Jn(x)=0的第m個正根。與該模式相對應的振動頻率為:

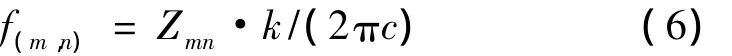
圖2a和圖2b分別是(0，1)模式和(1，1)模式由CCD拍攝的振動薄膜的變形條紋圖和對應的表面強度比值分布圖(即振動模式圖)。

Fig.2 Results of computer simulation at(0，1)mode and(1，1)mode a—(0，1)modeb—(1，1)mode

3 實驗結果

本文中通過實際測量薄膜的振動模式和3維面形結果來驗證方法的有效性，實驗裝置如圖3所示。

在半徑為100mm的圓形低音喇叭，覆蓋上一張繃緊的氣球薄膜，選定條紋周期為12個像素的正弦條紋進行投影，通過信號發生器輸出正弦激勵信號，驅動喇叭振動，這里近似認為薄膜振動的頻率和信號發生器激勵的頻率等同于薄膜振動的頻率。采集裝置為幀頻25frames/s的Baumer系列CCD相機。

Fig.3 Experimental setup

通過信號發生器改變薄膜受迫振動的頻率，可以得到相應的振動模式。圖4a～圖4e是5種不同激勵頻率下，CCD相機拍攝到的薄膜振動變形條紋圖和對應的振動模式圖。與該模式相對應的振動頻率f(m，n)是信號發生器激勵的正弦信號頻率。

Fig.4 Deformed fringe images and reconstructed vibration modes at different frequenciesa— f(0，1)=43.1Hz b—f(1，1)=68.8Hz c—f(2，1)=92.2Hz d—f(0，2)=99.1Hz e—f(1，2)=125.9Hz

為了進一步驗證該方法的可行性，本文中選用幀頻為1000frames/s的Basler A504K高速相機作為成像設備，對不同振動模式下的薄膜振動變形條紋進行采集。采用動態傅里葉變換輪廓術對采集到的變形條紋數據進行處理，過程如下:(1)從原始條紋圖中提取有效數據區域;(2)對得到的條紋圖進行傅里葉變換得到其頻譜;(3)選用合適的濾波窗對頻譜進行濾波，濾出相應的基頻;(4)對濾出的基頻進行頻譜移中后作逆傅里葉變換，得到截斷相位;(5)對截斷相位進行展開，得到任意采樣時刻薄膜振動的3維面形信息。

Fig.5 Restructed 3-D shape of vibrating membrane at(0，1)mode and(1，1)modea—(0，1)modeb—(1，1)mode

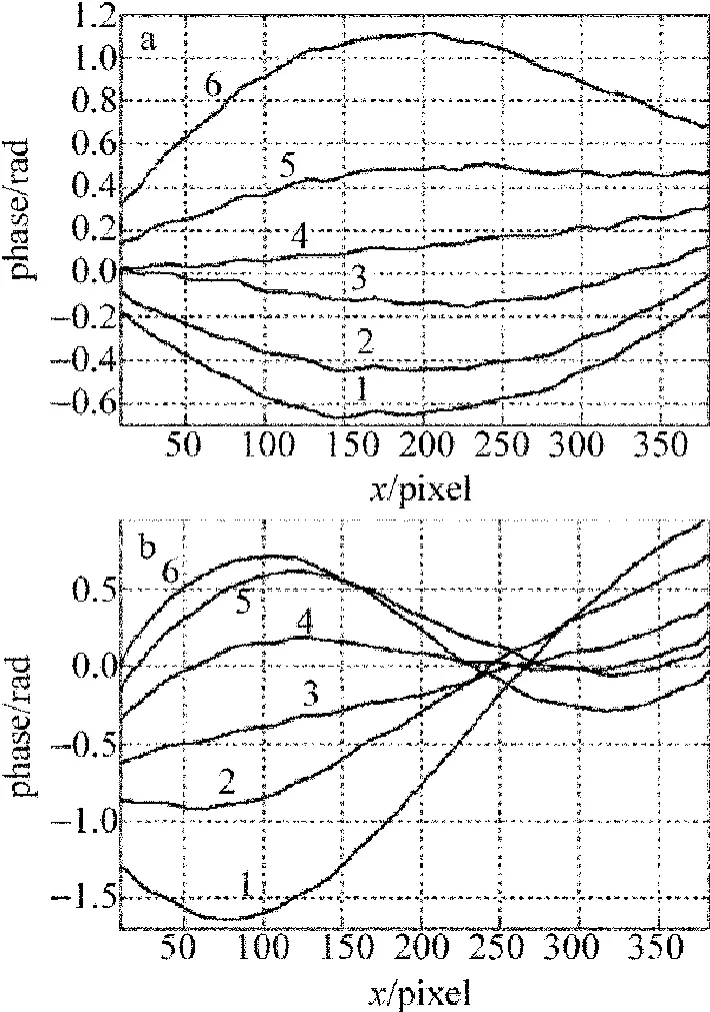
Fig.6 Middle line changes of vibrating membrane at(0，1)mode and at(1，1)modea—(0，1)modeb—(1，1)mode

選取(0，1)模式和(1，1)模式進行分析，其中圖5a和圖5b分別是(0，1)模式和(1，1)模式的其中一個時刻的3維動態面形。圖6a和圖6b是在相應振動頻率下，不同采樣時刻薄膜面形中間行的振動情況，數字1到6表示6個不同采樣時刻的面形振動情況，可以看出其振動變化規律基本吻合(0，1)模式和(1，1)模式，其中圖6a和圖6b中的第6個時刻對應圖5a和圖5b中的3維面形結果，可以看出，使用低頻CCD計算得到的振動模式基本反應了薄膜振動的變化。

根據(5)式、(6)式和給定的測量系統參量、圓形薄膜參量，通過計算機模擬計算得到各種振動模式下，對應的薄膜振動的頻率，如表1所示。

Table 1 Comparison of theoretical vibrating frequencies and practical results at different vibration modes

同時表1中還給出了實驗中得到的不同振動模式下薄膜做受迫振動激勵信號的頻率和理論模擬頻率與實際測量頻率值的比值。分析表中的數據可以看到，實際實驗中得到各個振動模式對應的頻率和模擬實驗得到的結果存在一定的誤差。誤差產生的主要原因是薄膜振動的頻率和信號發生器激勵的頻率并不完全相同，而且氣球薄膜在繃緊的過程中，表面的張力和自身的厚度都是不均勻的，影響了本文中的實驗結果，但二者吻合一致的模式-頻率關系驗證說明了本文中方法的有效性。

Fig.7 Comparison of theoretical vibration modes and practical vibration modes at different frequency excitation signals

圖7 顯示了薄膜在不同的振動頻率下，按照理論計算得到的振動模式和實際實驗測得振動模式的比較。通過圖6、圖7可以看出，利用第3節中提到的方法可以使用低幀頻的CCD快速獲取薄膜振動模式，更加有效地分析薄膜的振動情況。

4 結論

利用結構光投影技術和傅里葉條紋分析方法，對薄膜振動模式進行了理論分析，對比了振動模式的計算機模擬結果和實際測量結果。此外，在使用低幀頻CCD測量薄膜振動模式的同時，通過高速CCD得到相同頻率下薄膜振動的動態3維面形測量結果，印證了薄膜振動模式的可行性。與傳統的薄膜振動測量方法相比較，該方法具有速度快、成本低、數據處理量小等優勢。

［1］ WANG W C，HWANG C H，LIN S Y.Vibration measurement by the time-averaged electronic speckle pattern interferometry methods［J］.Applied Optics，1996，35(22):4502-4509.

［2］ MIRZA S，SINGH P，KUMAR R.Measurement of transverse vibrations/visualization of mode shapes in square plate by using digital speckle pattern interferometry and wavelet transform［J］.Optics and Lasers in Engineering，2006，44(1):41-55.

［3］ ZHANG C，FANG H，REN Y P，et al.Detecting vibration mode shapes by use of phase shifting digital speckle pattern interferometry［J］.Semiconductor Optoelectronics，1998，19(4):260-262(in Chinese).

［4］ JIA S H，LE K D，ZHAO H，et al.High/low-precision digital speckle pattern interferometry for vibration measurement［J］.Journal of Xi’an Jiaotong University，2000，29(2):126-129(in Chinese).

［5］ BUTTERS J N，LEENDERTZ J A.Speckle pattern and holographic techniques in engineering metrology［J］.Optics and Laser Technology，1971，3(1):26-30.

［6］ WANG C F，LIU L，WANG G B.Blurred image processing method for direction and amplitude measurement of high frequency vibration［J］.Journal of Vibration and Shock，2005，24(5):59-62(in Chinese).

［7］ ZHANG Q C.Technical study of three-dimensional shape measurement for dynamic process［D］.Chengdu:Sichuan University，2005:44-45(in Chinese).

［8］ ZHANG Q C，SU X Y.High-speed optical measurement for the drumhead vibration ［J］.Optics Express，2005，13(8):3310-3316.

［9］ ZHAI S L，GUO Z M，ZHANG Q C.Vibration mode analysis of membrane based on bi-color fringe projection［J］.Optics＆ Optoelectronic Technology，2013，11(2):59-66(in Chinese).

［10］ WEN Y F，SU X Y，ZHANG Q C，et al.Vibration mode analysis of films using time-average fringe method［J］.Journal of Optoelectronics Laser，2009，20(1):63-67(in Chinese).

［11］ WEN Y F，SU X Y，ZHANG Q C，et al.Vibration mode analysis of membrane using structured illumination time-average fringe method［J］.Optics＆ Optoelectronic Technology，2009，7(1):51-54(in Chinese).

［12］ CAO S P，WANG W F，XUE X C.Dynamic 3-D shape measurement based on de-interlaced images by Fourier transform［J］.Laser Technology，2013，37(6):736-741(in Chinese).