基于提升小波變換的紅外圖像雙重濾波算法

劉艾琳

(天津電子信息職業技術學院數字藝術系，天津300350)

引 言

紅外圖像總體上對比度較低，且由于成像環境復雜以及在傳輸存儲等環節中，不可避免受到噪聲的干擾，導致所獲取的圖像一般來說是降質圖像。KANG［1］等人基于紅外圖像的自相似統計特征提出一種兩階段3維濾波算法;WANG［2］等人將偽中值濾波與小波變換相結合用于紅外圖像處理;YU［3］等人提出一種基于混合雙邊濾波的紅外圖像自適應濾波算法;HU［4］等人將同態濾波用于紅外圖像增強研究，取得了不錯的效果;ZHANG［5］提出一種針對紅外圖像中的顆粒噪聲的濾波算法。近年來該領域的研究成果特點有:(1)針對紅外圖像濾波增強的研究，主要基于空間域進行，較少利用多尺度分析方法，如小波變換、提升小波變換等;(2)對于紅外圖像濾波與增強基本是分開研究，并未作為一個整體進行，即對圖像噪聲的濾波，較少考慮到濾波后圖像視覺效果;對圖像增強處理并未考慮到圖像受到噪聲干擾這一特殊情形。

提升小波變換與傳統建立在傅里葉變換基礎上的小波變換的區別主要有:(1)傳統小波變換通過將小波母函數伸縮或者平移來構造小波基函數，運算效率較為低下;而提升小波變換采用“分步驟”的思想來實現小波變換，即采用預測和更新兩個環節實現對圖像高頻和低頻信息的高效率分離，計算效率得到提高;(2)提升小波變換通過原位操作，能夠實現圖像的整數小波變換，在分解和重構過程中對圖像信號刻畫更為精確，這也是傳統小波變換所不具備的。近年來，提升小波變換以其優良的特性在圖像濾波［6］、圖像復原［7］、圖像重構［8］等方面得到成功的應用，但就目前公開發表的研究成果來看，提升小波變換在紅外圖像處理方面應用較少。

作者將圖像濾波和增強方法有機結合，借助提升小波變換理論框架，提出了一種基于提升小波變換的紅外降質圖像的雙重濾波方法。

1 紅外圖像提升小波變換流程分析

一幅紅外圖像可表示成一個信號序列的集合Sj={Sj，k}，對該圖像采用單層提升小波變換，主要流程如下。

(1)分解。將上述信號集合分解成偶序列η2j和奇數序列φ2j-1，并且該兩類序列彼此互不相交，該步驟中圖像信號序列可表示成:

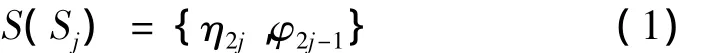
(2)預測。該步驟是基于圖像信號間存在相關性這一前提，采用相鄰信號偶數序列對奇數序列進行預測，通過對奇數序列的真實值與預測值做差，該差值可稱為細節系數，預測步驟可定義為:

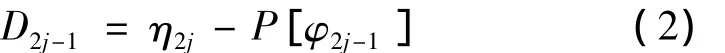
式中，D2j-1為細節系數，P［·］代表預測算子。

(3)更新。采用更新算子U［·］對第(2)步中產生的序列D2j-1進行更新，其過程為:

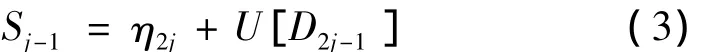
2 一種新型小波域閾值函數模型

近年來，在經典硬閾值、軟閾值函數模型的基礎上，提出了一系列的改進函數模型。

(1)折中法的改進閾值模型，該模型通過對增加一定的調節因子，對經典的軟、硬閾值進行改進，在一定程度上提高了濾波效果，該閾值模型代表性的一類如下表示:

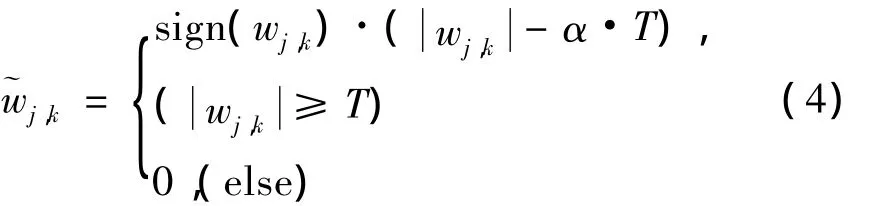
(2)指數型改進閾值函數模型，該類模型通過對經典閾值函數模型中增加指數型的調節系數，來實現對濾波效果的改進，代表性的函數模型如下所示:

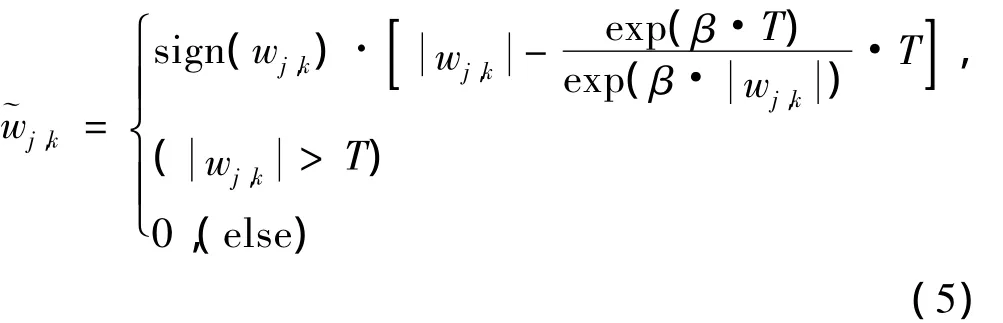
上述兩類函數都是通過增加調節因子來實現對經典閾值函數存在缺陷進行一定程度的修正。不足之處在于:(1)模型中的調節因子的功能是對函數模型的過度濾波現象進行修正，而事實上圖像受到的噪聲強度是不同的，采用千篇一律的調節因子，濾波效果沒有從根本上得到提高;(2)閾值的單一性，特別是對于提升小波變換而言，圖像經過多層小波變換后的小波系數幅值會隨著分解層數的增大而快速衰減，而相應的閾值并未隨之進行改變。鑒于紅外圖像噪聲強度大，且對比度較低，結合以上對兩類改進閾值函數模型特性分析結果，提出一種新型提升小波變換的閾值函數模型:

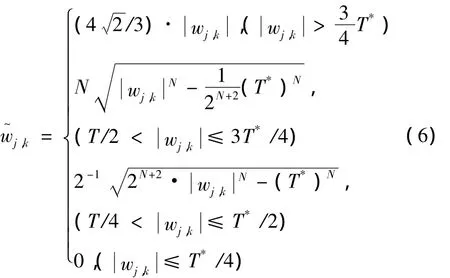
式中，N為小波分解層數，T*為新型小波系數閾值。經典軟硬閾值以及上述(4)式和(5)式描述的改進型閾值函數均采用如下閾值選取策略:

式中，x和y分別為圖像尺寸大小，σ為小波分解系數的均方差:

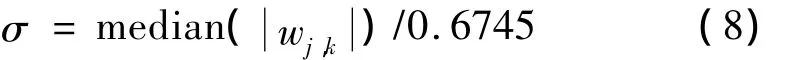
可以看出，該閾值屬于全局閾值范疇，即無法根據小波分解層數的變化而自適應進行調整，理論上講，隨著小波分解層數的增加，小波系數幅值快速衰減，那么，對應的閾值也應當呈現這一特征，對此，作者提出一種新型閾值計算方法:

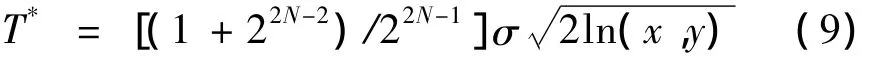
3 改進非均局部均值濾波算法

紅外噪聲圖像可采用如下模型表示:

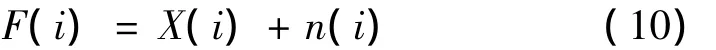
式中，X(i)為紅外圖像有用信號，n(i)則為噪聲信號。對于噪聲圖像中任一像素點，采用非局部均值濾波進行處理時，是通過求取該圖像中所有像素點灰度值的加權平均值作為該點的濾波結果:

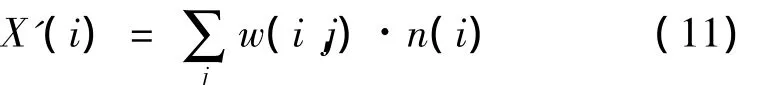
式中，X′(i)為濾波后的紅外圖像信號，n(i)為噪聲信號，w(i，j)為權值，且j取任意正整數。權值w(i，j)是根據圖像上任意兩個像素點間的相似程度來進行賦值，而兩點間的相似程度由兩者的灰度值矩陣進行決定。一般來說，采用兩點間的灰度值矩陣的歐氏距離來衡量兩者的相似程度，即:式中，Ni，Nj分別表示像素 i，j對應的灰度值矩陣，a為高斯加權標準差值。那么，權值w(i，j)則可進行如下計算:式中是歸一化參量，f(·)為核函數，在某種程度上決定著該算法的成敗，對于經典非局部均值濾波而言，該核函數為:

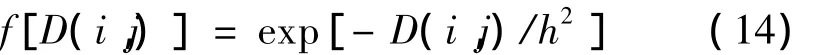
式中，h為衰減因子，其功能在于控制函數的衰減，從而影響最終的濾波效果。函數的類型多種多樣，一般來說主要有余弦型和高斯型兩類核函數:

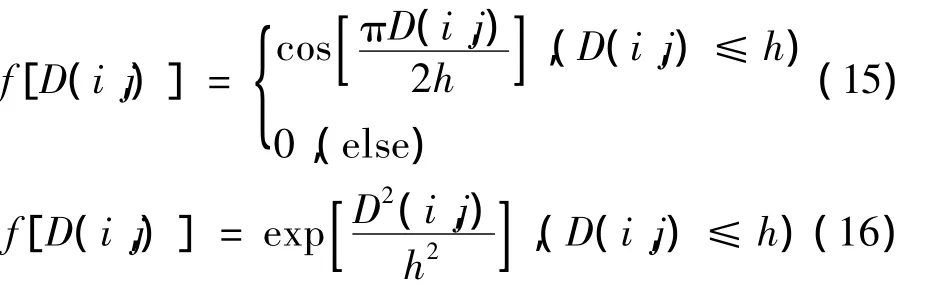
相關研究成果表明［9］，經典非局部均值中的指數型核函數對于強度較低的噪聲濾波效果較為理想，當噪聲持續增大時，效果則出現明顯下降;而余弦型核函數濾波性能則與之相反，兩者具有一定的互補作用。因此，本文中將兩者有機結合，提出一種基于新型核函數模型，該模型如下表示:

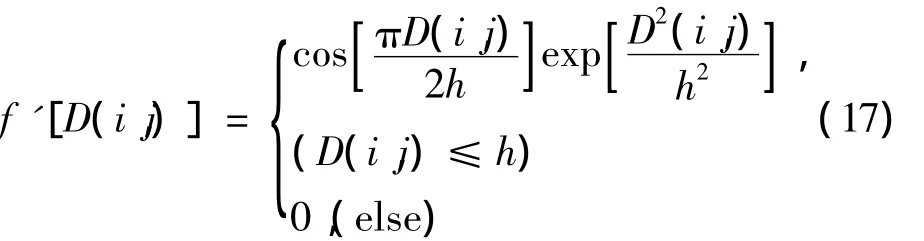
該模型對經典非局部均值濾波算法中的指數型核函數增加了一個余弦型核函數作為其系數，以此來對原有的經典指數核函數濾波性能進行一定程度的提升。

4 算法基本流程及實驗仿真分析

4．1 算法基本流程

步驟1:對紅外噪聲圖像進行提升小波變換，獲得噪聲圖像的低頻和高頻提升小波變換子圖像。

步驟2:對低頻提升小波變換子圖像再次執行提升小波變換，獲得次高頻分解子圖像1和次低頻分解子圖像1，鑒于紅外圖像絕大部分的背景信息主要集中于次低頻分解子圖像1中，該部分信息的存在反而會導致紅外圖像整體上偏暗，少量的有價值的目標信息被湮沒，因而加以舍棄;采用(6)式所定義的自適應小波閾值去噪算法來對抑制該部分圖像中的噪聲。

步驟3:對高頻提升小波變換高頻子圖像再次執行提升小波變換，獲得次高頻分解子圖像2和次低頻分解子圖像2，鑒于噪聲主要集中于次高頻分解子圖像2中，因而加以舍棄;采用改進非局部均值濾波算法去除次低頻分解子圖像2中存在的噪聲。

步驟4:將步驟2和步驟3中濾波后的提升小波變換子圖像進行重構，獲得去噪后的紅外圖像。

步驟5:對步驟4中獲得的去噪圖像采用直方圖均衡化算法處理，以提高去噪后圖像的視覺效果。

4．2 實驗仿真分析

采用Lena標準測試圖像以及一幅紅外圖像來對本文中的算法進行性能測試。此外，采用經典非局部均值濾波算法(non-local means，NLM)、小波閾值函數濾波算法［6］以及改進型非局部均值濾波算法(improved non-local means，INLM)［9］分別對上述圖像進行去噪實驗，并將其實驗結果與本文中算法的實驗結果進行對比。對于濾波結果的評價，選用應用較為廣泛的峰值信噪比(peak signal-to-noise ratio，PSNR)［10］以及結構相似度(structural similarity，SSIM)［11］作為濾波后圖像質量定量評價指標。Lena標準測試圖像實驗結果見圖1、表1和表2。

Fig.1 Comparison of the denoising results of Lena imagea—noise image(30%) b—NLM c—algorithm［6］ d—algorithm［9］e—algorithm proposed

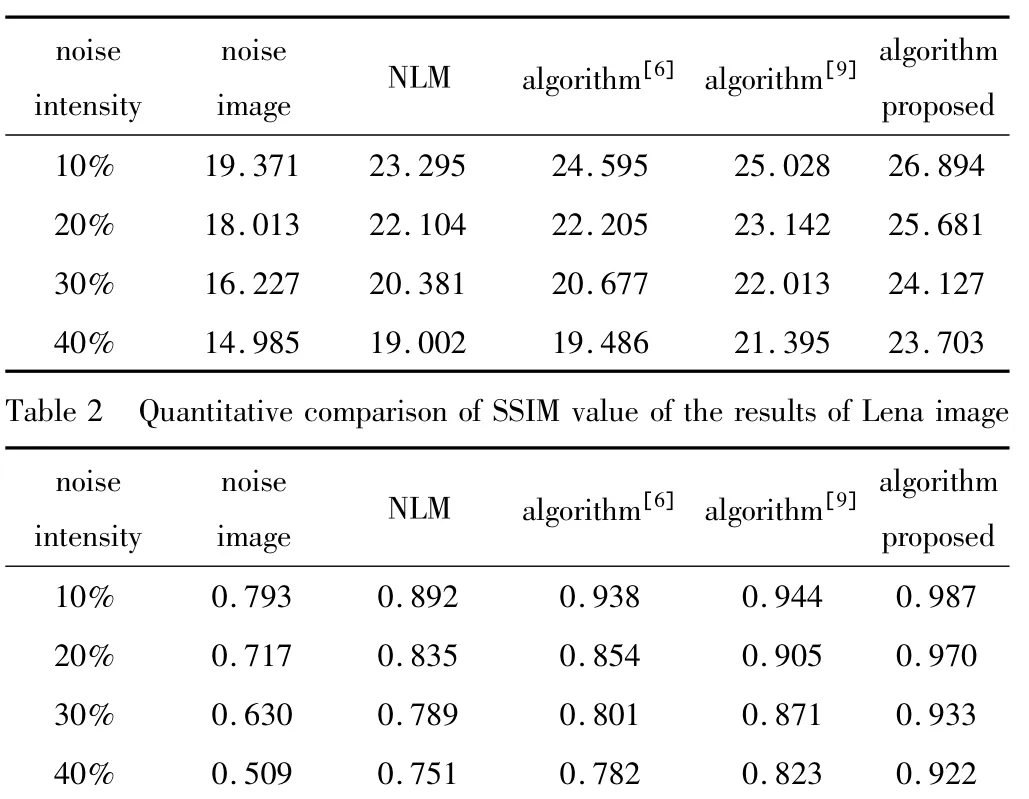
Table 1 Quantitative comparison of PSNR value of the results of Lena image/dB

從圖1b可以看出，圖像中噪聲殘留程度較高，圖像相對于噪聲圖像(見圖1a)而言，視覺效果并未得到改善;采用參考文獻［6］中所定義的輪廓波變換域新型閾值函數進行濾波，從圖1c中可以看出，噪聲得到抑制，但仍有大量殘余，相對于經典非局部均值濾波算法而言，改進小波閾值算法［6］性能還是較優的;從圖1d中可以看出，改進非局部均值濾波算法［9］性能不但優于經典非均值濾波算法而且優于改進小波閾值算法［6］。但就濾波后圖像以及表1、表2中的數據可以看出，本文中算法性能總體上優于前幾類算法，并且圖1e相對于圖1b～圖1d來說，圖像信息得到增強，對比度得以改善，這主要得益于本文中算法增加了一個圖像增強環節。

為了更好地用本文中的算法對紅外圖像的濾波性能進行測試，仍采用上述幾類算法分別與本文中的算法對1幅熱紅外飛機圖像進行實驗，實驗結果分別如圖2、圖3和表3、表4所示。

Fig.2 Comparison of the denoising results of plane imagea—noise image(20%) b—NLM c—algorithm［6］ d—algorithm［9］e—algorithm proposed

Fig.3 Comparison of the denoising results of plane imagea—noise image(40%) b—NLM c—algorithm［6］ d—algorithm［9］e—algorithm proposed

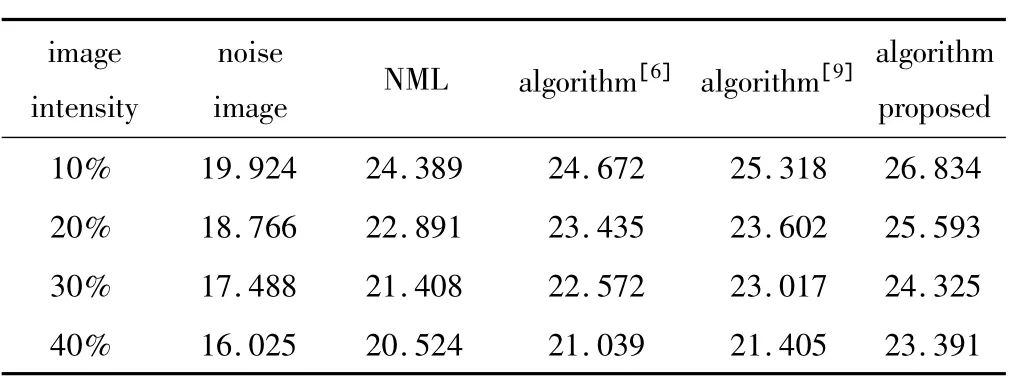
Table 3 Quantitative comparison of PSNR value of the results of plane image/dB

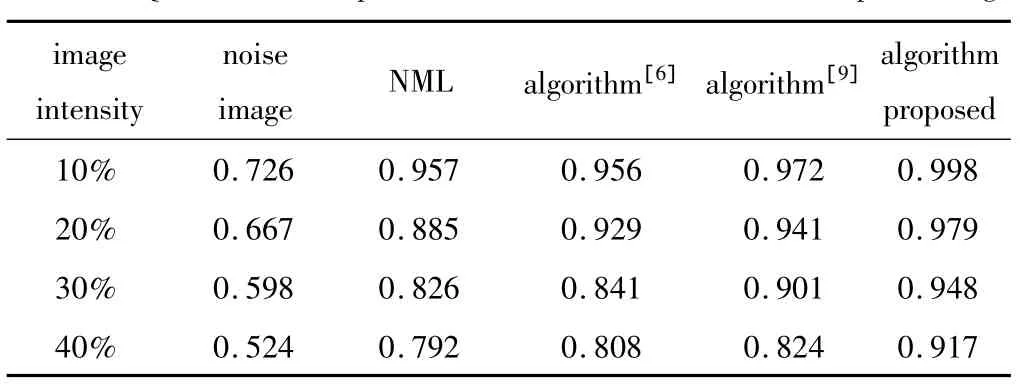
T e

結合表3、表4以及圖2、圖3的實驗結果分析可以看出，在對紅外圖像(飛機)加入10% ～40%強度的噪聲過程中，經典非局部均值濾波算法、改進小波閾值算法［6］、改進非局部均值濾波算法［9］以及本文中算法性能均有所下降，但本文中算法性能下降幅度最小(PSNR值下降約4dB)，這說明，該算法具有較好的抗噪性。從圖2e和圖3e可以看出，圖中目標物——飛機的輪廓基本從噪聲中恢復出來，且能清晰辨認。

5 結束語

為了有效濾除紅外圖像中的噪聲，提出了一種基于提升小變換的紅外圖像雙重濾波算法。標準測試圖像和紅外圖像濾波結果證明，本文中算法的PSNR和SSIM等指標值均優于經典非局部均值濾波、改進小波閾值法以及改進非局部均值濾波算法。就算法計算效率而言，盡管通過舍棄相當一部分小波分解系數以提高算法計算速度，但由于對圖像先后實現兩次提升小波變換，無疑在一定程度上增加了算法耗時。因此，大幅度提高算法計算效率，是本文中算法需要改進之處。

［1］ KANG Ch Q，CAO W P，HUA L，et al.Infrared image denoising algorithm via tow-stage 3-D filtering［J］.Laser ＆ Infrared，2013，43(3):261-264(in Chinese).

［2］ WANG X W，WANG Sh L，LI K.Infrared image enhancement based on pseudo median filter and wavelet transform［J］.Laser＆ Infared，2013，43(1):90-93(in Chinese).

［3］ YU B，GAO L，ZHAO T Y，et al.Adaptive hybrid bilateral filtering algorithm for infrared iamge［J］.Infrared and Laser Engineering，2012，41(11):3102-3107(in Chinese).

［4］ HU D M，ZHAO H Sh，LI Y Ch，et al.A new approach to infrared image enhancement based on homomorphic filter［J］.Infrared Technology，2012，34(4):224-228(in Chinese).

［5］ ZHANG C T.A new adaptive filtering algorithm based on salt＆ pepper noise in infrared image［J］.Infrared Technology，2013，35(8):502-506(in Chinese).

［6］ CAO X Y，ZHANG Zh J，XING J J.Method of radar signal denoising based on lifting waveelt improved threshold［J］.Computer Engineering and Applications，2012，48(14):143-147(in Chinese).

［7］ HUANG D T，WU Zh Y.Application of lifting wavelet transform in blind restoration scheme based on NAS-RIF algorithm［J］.Journal of Computer-Aided Design ＆ Computer Graphics，2012，24(12):1614-1620(in Chinese).

［8］ HOU X S，ZHANG L，XIAO L.Areconstruction algorithm with Bayesian compressive sensing for synthetic aperture radar images［J］.Journal of Xi’an Jiaotong University，2013，47(8):74-79(in Chinese).

［9］ LIU X M，TIAN Y，HE H，et al.Improved non-local means algorithm for image denoising［J］.Computer Engineering，2012，38(4):199-201(in Chinese).

［10］ LU Zh L，LI R L，LI T，et al.Infrared image denoising based total variation theory［J］.Laser Technology，2012，36(2):194-197(in Chinese).

［11］ TIAN H N，LI S M.Objective evaluation method for image quality based on edge structure similarity［J］.Acta Photonica Sinica，2013，42(1):110-114(in Chinese).