基于軌跡線性化控制的再入軌跡跟蹤制導

沈作軍，朱國棟

(北京航空航天大學 航空科學與工程學院，北京 100191)

再入制導是指通過在線產生指令引導具有一定升力能力的再入飛行器從當前狀態安全到達指定終端狀態的過程［1］.再入制導的核心是通過有效控制耗散能量，并滿足過程物理約束和終端狀態約束.飛行器一般為無動力再入，必須一次成功;同時要求制導律能夠適應初始再入狀態、氣動、風場等方面的不確定性及可能的任務改變、終止或控制能力減弱的情形.

再入制導中的一類重要算法是軌跡跟蹤制導，包括參考軌跡設計和軌跡跟蹤兩部分.制導律通過比較當前狀態和參考軌跡之間的偏差產生迎角和傾側角指令.軌跡跟蹤制導以航天飛機的再入制導律為典型代表［2］.航天飛機制導律設計包括參考阻力加速度剖面設計和在線的參考剖面跟蹤.規劃阻力參考剖面時主要考慮到縱程要求和滿足過程約束.但實際上在規劃時往往耗時耗力，參數需要反復試湊，在實際飛行和地面任務設計相差較大時，飛行器甚至可能無法安全返回.

為了提高再入制導的自主性和適應性，近年來專家學者們提出了多種再入參考軌跡的在線生成方法.文獻［3］利用“擬平衡滑翔條件”將過程約束轉換為對速度滾轉角的約束，將非線性軌跡規劃問題轉化為順序進行兩次單參數搜索問題，能夠快速生成滿足所有約束條件的三自由度軌跡.文獻［4］研究了最優阻力加速度剖面的在線生成方法，避免了地面的離線規劃.文獻［5］提出了在阻力加速度剖面規劃參考軌跡，同時考慮到縱程和橫程要求的軌跡快速生成算法.一旦在線參考軌跡生成，需要研究如何實現對參考軌跡的精確跟蹤.應用于航天飛機阻力剖面跟蹤的反饋線性化方法是軌跡跟蹤的基準控制算法.文獻［6］給出了一種近似反饋線性化方法，對三維軌跡的跟蹤轉換為對橫程和縱程的跟蹤，但僅對無拉偏的理想情況做了分析;反饋線性化方法在模型存在較大不確定性時(如驗證飛行時)，非線性項無法進行精確對消，控制性能將變差甚至可能失穩.線性二次型調節器(Linear Quadratic Regulator，LQR)控制由于反饋增益可以采用誤差狀態的線性反饋控制律構成最優閉環，設計時能夠考慮允許的狀態偏差和控制量偏差等多個指標，在參數不確定的情況下閉環系統也具有一定魯棒性，在多入多出系統的控制方面獲得了較多應用.文獻［7］指出，基于LQR方法計算得到的反饋增益對于同一飛行器能夠適用于不同再入參考軌跡的跟蹤，且對初始條件的拉偏具有較好的魯棒性;離線生成的最優增益具有在線應用于軌跡跟蹤的潛力.但文獻同時指出，LQR控制效果和精度依賴于參考軌跡特性，特別當軌跡傾角較陡時，跟蹤精度將明顯降低.文獻［8］提出了一種封閉形式的近似滾動時域控制(Receding Horizon Control，RHC)方法，避免了在線積分和顯式的增益調度;相比LQR方法，滾動時域控制對權重矩陣參數的選取較不敏感;方法能夠實現三維軌跡的精確跟蹤并能理論上保證閉環穩定性，但預測步長較多時計算量稍大.

軌跡線性化控制(Trajectory Linearization Control，TLC)方法是一種基于微分代數譜理論的非線性控制方法，在NASA先進制導控制項目中被成功應用于X-33的上升段姿控系統設計［9］.本文將TLC方法在升力體飛行器設計中的應用從姿態回路擴展到制導回路，并結合利用“擬平衡滑翔條件”的在線軌跡生成算法［3］，提出了一種基于TLC理論的再入軌跡跟蹤制導律.TLC方法利用再入飛行器固有時間尺度分離的特點，將控制變量進行有效降階，在高度環路和速度環路分別利用閉環譜配置對跟蹤誤差進行鎮定，并能保證指數穩定性.新制導律通過與基于LQR和近似滾動時域控制的制導方法進行比較并經過三自由度蒙特卡羅拉偏仿真進行驗證，證明了其有效性.

1 制導問題描述

1.1 再入動力學方程

滑翔再入飛行器相對旋轉正地球的三自由度無量綱質點動力學方程［10］為

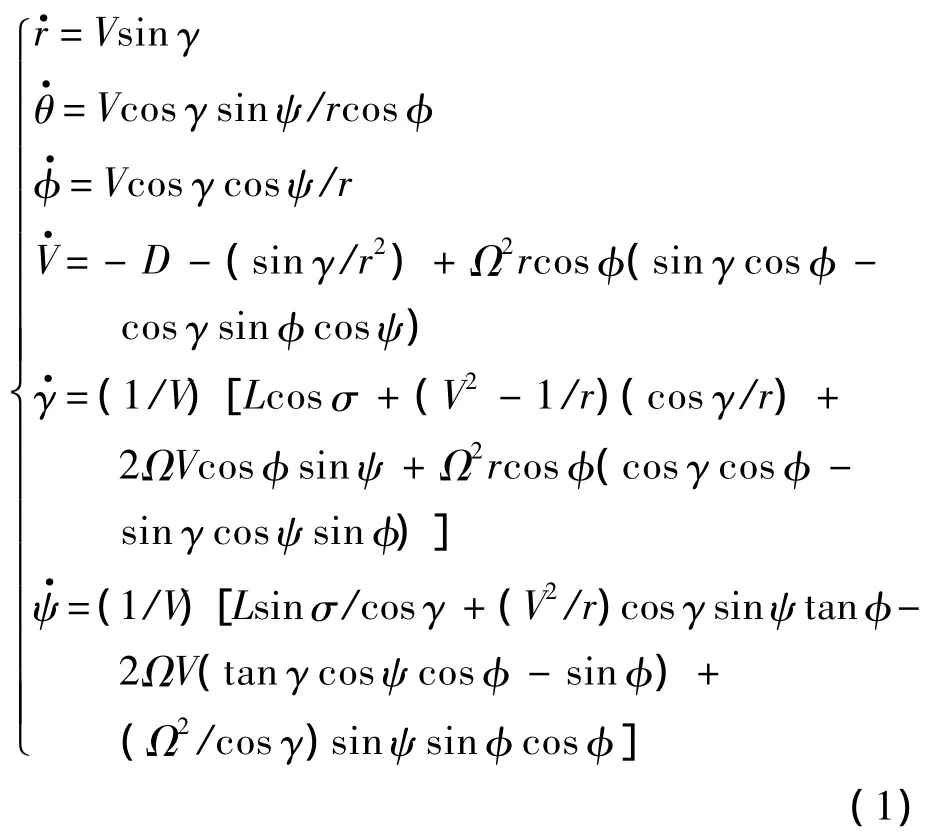
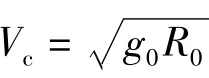
1.2 再入軌跡約束條件

再入軌跡需要滿足的約束包括過程約束和終端約束.常見的過程約束包括熱流、動壓q和法向過載約束nz，

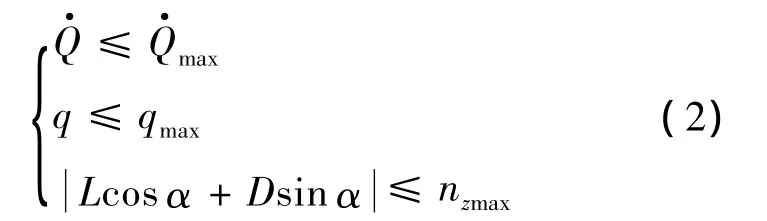
距著陸場一段距離時飛行器將進入末端能量管 理 段 (Terminal Area Energy Management，TAEM).再入段和TAME段在交接班時需滿足一定的終端約束，包括高度約束rf、速度約束vf、航程約束sf和傾側角約束σf，

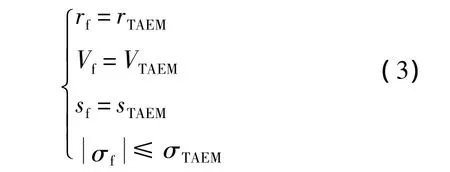
式中:rTAEM、VTAEM和sTAEM分別為TEAM時的r、V和s，s為航程;σTAEM為交接班時允許的σ最大值.

1.3 飛行器模型

通用航空飛行器(Common Aero Vehicle-H，CAV-H)［11］是一種亞軌道升力體式再入飛行器，最大升阻比約為3.5.CAV-H由于升阻較大，機動能力強，能夠實現較高的落點精度，且能從多種武器平臺發射，因而和Hypersonic Technology Vehicle-2(HTV-2)一樣作為美國未來實現全球打擊的戰略武器.本文以CAV-H模型為對象進行再入段設計.

1.4 參考軌跡分析

文獻［3］將再入軌跡設計分為3段(如圖1所示):初始下降段、擬平衡滑翔段和Pre-TAEM段.初始下降段的主要作用是通過軌跡積分預測，引導飛行器進入再入走廊并保證與擬平衡滑翔段光滑銜接.擬平衡滑翔段是再入飛行的主要階段，這一階段的特點是軌跡傾角較小(＜－1°)且變化較慢.對于低升阻比飛行器如X-33和X-38，再入飛行末段即Pre-TAEM段，這一段升力不足以維持平緩的滑翔飛行，軌跡傾角變化較為劇烈.對于高升阻比飛行器如航天飛機，文獻［3］提出的“擬平衡滑翔條件”直到再入末端仍然可以較好滿足，可以不再劃分Pre-TAEM段.基于文獻［3］提出的算法生成的參考軌跡可以滿足第1.2節給出的動力學方程組(式(1))和所有軌跡約束條件.

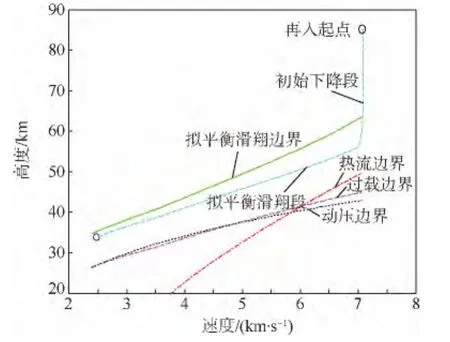
圖1 再入軌跡的構成Fig.1 Composition of entry trajectory

本文研究針對實現以Pre-TAEM狀態為終端條件的擬平衡滑翔段縱向參考軌跡的精確跟蹤.在參考軌跡跟蹤時，將傾側角作為主要控制量;考慮到配平要求和熱流限制，迎角剖面預先給定為某一隨馬赫數變化的函數，并對偏離給定迎角剖面的最大值給出限制.

2 軌跡跟蹤制導律設計

2.1 TLC 理論

TLC(其概念如圖2所示)結構由兩部分組成:通過非線性模型偽逆求得給定標稱輸出)對應的標稱控制量，以粗略對消系統的非線性，并將一般的軌跡跟蹤問題轉化為在誤差坐標系的狀態調節問題，上方帶“－”的變量為變量的標稱值;將非線性時變誤差動力學方程組線性化，通過李雅普諾夫坐標變換將一般的線性時變方程組轉化為線性時變系統標準型，并通過配置Parallel Differential Spectrum(PD譜)對誤差動態進行鎮定.反饋控制項由時變鎮定控制器產生，并可寫為狀態誤差量的線性反饋形式.上方帶“～”的變量為變量的狀態誤差量.非線性模型中的 ξ(t)、μ(t)、η(t)和 θ(t)分別為狀態、輸入、輸出和時變參數向量.f(·)和g(·)為非線性向量函數.關于非線性偽逆和PD譜配置的理論見文獻［12］.

TLC對跟蹤誤差信號可以保證指數穩定性，閉環系統對正則擾動及奇異攝動都有很好的適應性.

圖2 TLC概念圖Fig.2 Conceptual configuration of TLC

2.2 環路劃分和獨立變量的選取

飛行器動力學不同狀態變量在時間尺度上存在明顯差異這一事實在航空航天領域被廣泛應用于軌跡優化、控制律設計和系統分析中［13-15］.利用時間尺度分離的特性，控制設計展現出的優勢是可以減小控制變量個數并避免積分時由于不同變量變化速率不同帶來的剛性數值問題.

TLC的控制策略是基于奇異攝動理論中的時間尺度分離思想，將全量、剛體的飛行器動力學模型分為2個回路，即制導回路(其TLC結構如圖3所示，帶角標C的變量為環路的控制輸出)和姿態回路;4個環路，對應高度(極慢動態)、速度(慢動態)、姿態角(較慢動態)和姿態角速率(快動態)環路，分別進行設計.本文分析僅涉及包含高度、速度環路的制導回路設計.

圖3 制導回路TLC結構圖Fig.3 Configuration of TLC in guidance loop

在軌跡跟蹤制導中，當獨立變量從與狀態無關的時間變為與狀態相關的單調變量時可以減小狀態方程維數并增加控制的魯棒性［7］.兩個可取的與時間相關的單調變量為能量e和已飛地球大圓距離sTravel(即為已飛航程).本文選取sTravel為獨立變量，認為軌跡在線生成后儲存為以sTravel為獨立變量的數表;能量為獨立變量時的控制器設計是相似的.

2.3 高度環路設計

在高度環路，軌跡傾角相對于高度變化是快動態，故將軌跡傾角取作高度控制的虛擬控制量.由于參考軌跡中包含了滿足縱向動力學約束的軌跡傾角信息，故可直接從參考軌跡中取得高度環路的標稱控制量.為了改善穩態性能和提高對模型不確定性和擾動的魯棒性，采用比例積分控制，狀態變量及其標稱值分別為:反饋控制量為，標稱值為定義狀態誤差量為獨立變量，對狀態的積分和求導都應對sTravel進行.sTravel對時間的導數為

式中:Δψ為速度航向角和視線角的夾角.當再入任務要求飛行較大橫程時，保留Δψ項并根據飛行任務取Δψ=5°～10°將一定程度上補償用地球大圓近似已飛航程的偏差影響.將d(·)/d sTravel記為(·)'，則高度對航程的導數為

狀態誤差量的線性化方程為

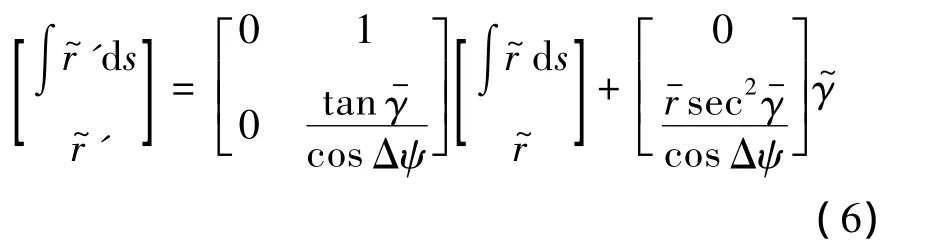
期望配置的閉環誤差動態(以下將sTravel簡寫為s)為

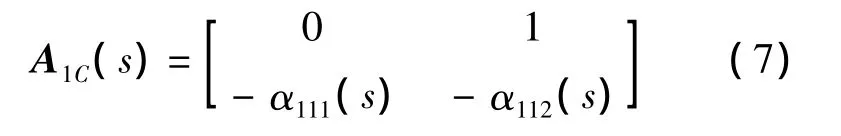
式中:αijl為閉環動態矩陣參數，下標 i、j和 l分別為環路數、解耦后環路的第j個子動態和子動態的第l個參數.

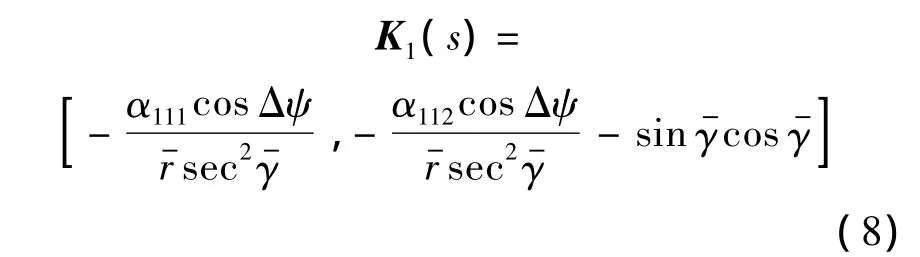
2.4 速度環路設計

速度環路迎角和傾側角相對速度和彈道傾角的變化是快動態，因而作為速度和彈道傾角跟蹤的控制量.與高度環路相同，標稱迎角α－和傾側角指令同樣可直接從參考軌跡中取得.采用比例積分控制，系統狀態變量及其標稱值分別為

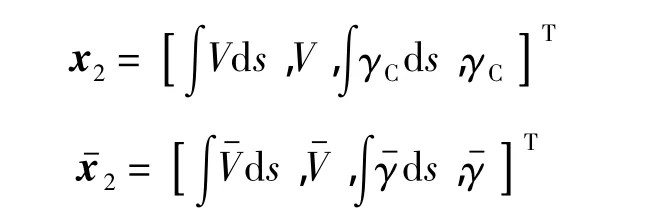
狀態誤差量為

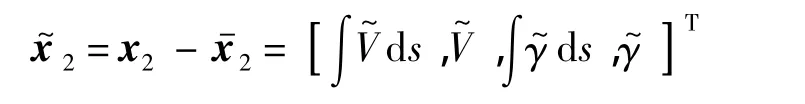
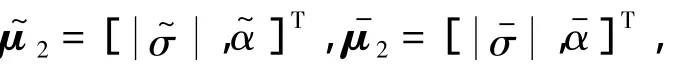
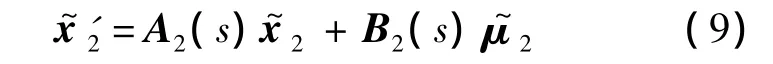
式中:A2和B2分別為速度環路的狀態矩陣和控制矩陣.

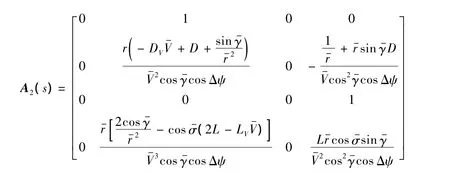
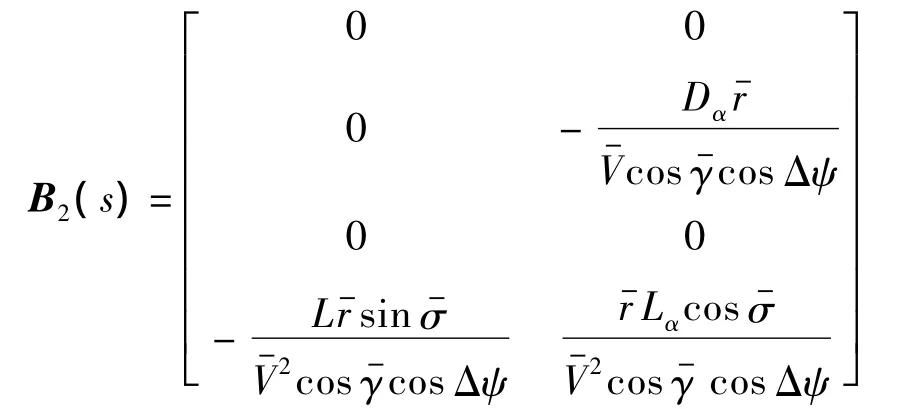
式中:DV和LV分別為D和L對V的導數;Dα和Lα分別為D和L對α的導數.

期望配置的閉環動態誤差為

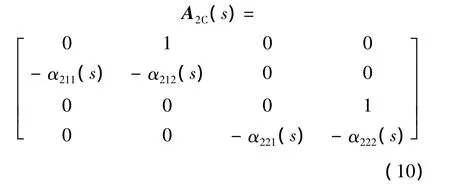
閉環二的反饋控制量為

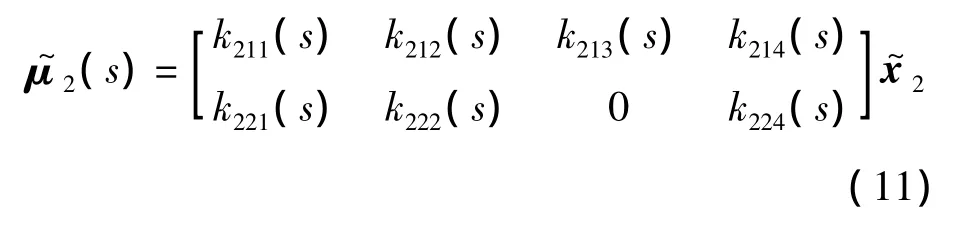
式中:

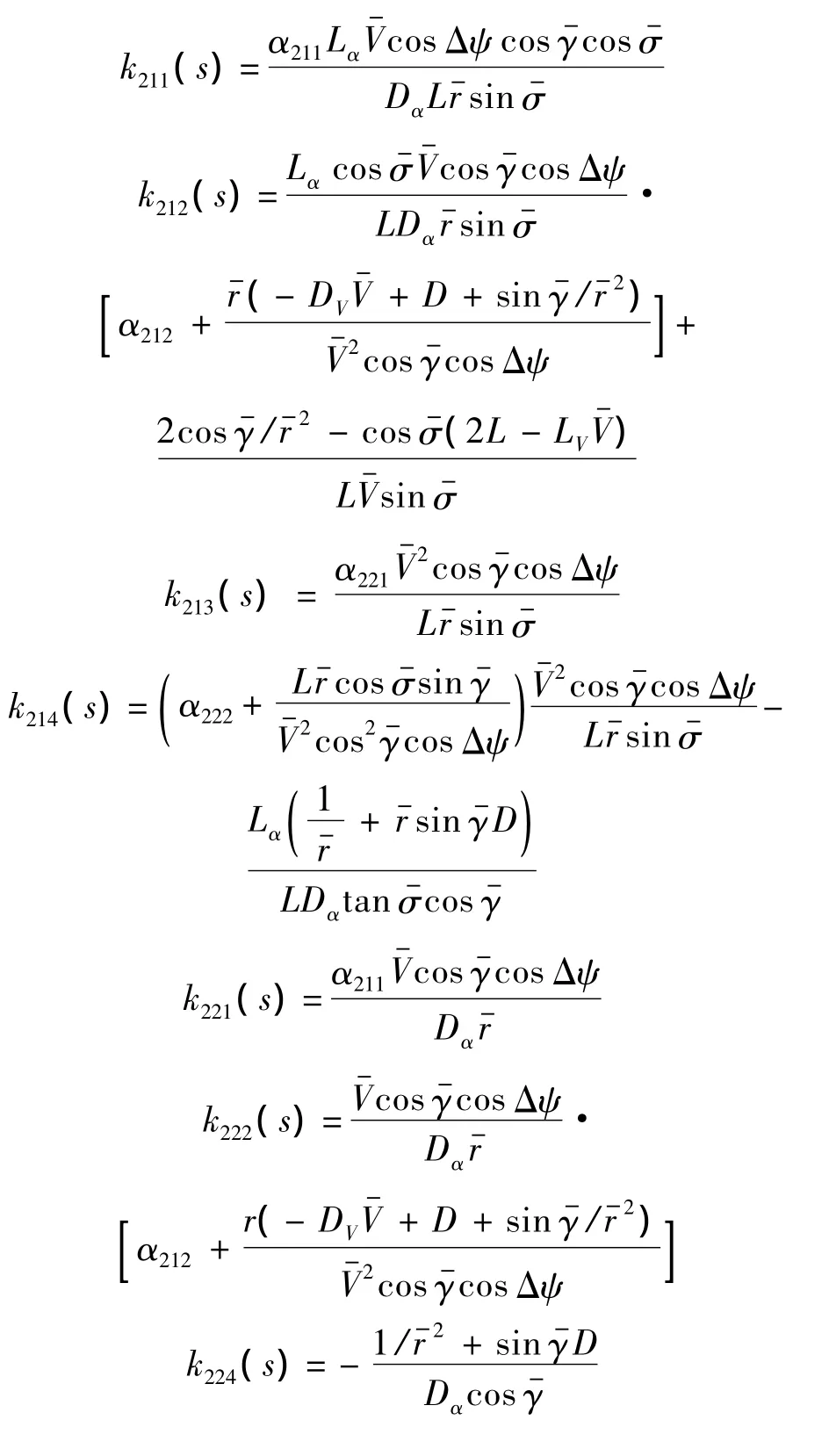
注意到當標稱傾側角為零，不能滿足PD譜配置關于控制矩陣必須列滿秩的條件［9］.但在基于“擬平衡滑翔條件”的在線軌跡設計中，為防止傾側角控制飽和，沿軌跡的標稱傾側角都不接近于零(文獻［9］中圖8虛線)，因此使用基于TLC的跟蹤制導律不存在障礙.

3 控制器參數設置與調整

兩環路配置的閉環動態矩陣中的參數αijl(s)，i=1，2，j=1，2，l=1，2 是通過閉環二階PD譜得到

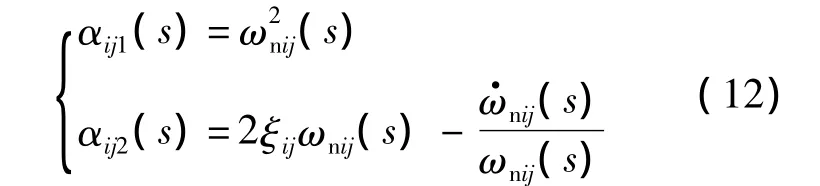
式中:ξij為常值阻尼比;ωnij為時變帶寬.文獻［12］指出，以時間自變量的誤差系統，當t＞0時，滿足ξij(t)＞0，ωnij(t)＞0時，系統閉環穩定;sTravel作為單調變量，證明中作符號替換，同理可證誤差系統閉環穩定.控制系統在設計時是基于時間尺度分離方法，要求內環路的帶寬相對于外環路要充分大，以滿足奇異攝動理論的要求.

二階PD譜阻尼和自然頻率的意義可以參考二階線性定常系統:阻尼比決定超調量，自然頻率決定響應速度、控制用量和有限時間內的控制精度，參數和控制響應有直接對應關系.阻尼比調參可從二階系統最佳阻尼比0.7開始，并根據實際時域響應情況適當增大阻尼比.對于以時間為自變量跟蹤的制導律，速度環路的自然頻率可以取為姿態角環路頻率的1/5～1/3;高度環路也取為速度環路頻率的1/5～1/3;環路自然頻率初值的選取可參考飛行器本體長短周期的模態頻率.

隨著距目標點距離的減小，速度減小，對飛行器高度和速度控制精度的要求提高;而在再入中間過程中又不希望過短的調節時間要求導致翻轉過程中傾側角的超調過大.為更好兼顧過程飛行和終端約束的要求，兩環路自然頻率取為無量綱速度的線性函數形式(見表1).

表1 高度和速度環路參數Table 1 Altitude and velocity sub-loop parameters

4 仿真驗證

這里用LQR方法和滾動時域控制作為基準控制方法與TLC的控制效果進行比較.LQR方法和滾動時域控制方法所用小擾動方程也是以sTravel為自變量線性化得到的.LQR方法用迎角、傾側角跟蹤高度、軌跡傾角和速度.

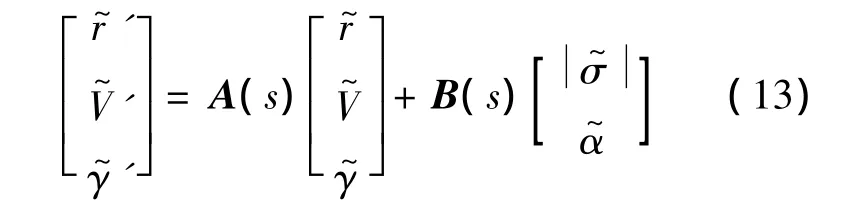
LQR權重矩陣按文獻［7］中的偏差量原則選取，其中 Q=diag［4 ×109，2.5 ×106，3.28 ×105］，R=diag［3.28 ×103，25］.滾動時域控制用迎角和傾側角鎮定高度和速度偏差，權重矩陣取為Q'=diag［1，1］，R'=diag［100，0.1］.初始再入時步長取h=0.006，線性過渡到再入末端時的h=0.0045，步數N=7.側向制導律使用航向角誤差漏斗邏輯［2］.為更好地對比不同控制方法高度和速度跟蹤精度，仿真截止條件取為2 300m/s的Pre-TAEM速度對應的sTravel(這里統一取為距離TAEM 300 km)，并要求飛行器大致指向目標.

三自由度拉偏仿真的設置條件見表2，但為了統一仿真終端的參考高度和速度，對比三種控制方法時未對再入初始條件進行拉偏，使用相同的參考軌跡.為了更好顯示不同控制方法終端速度-高度的分布情況，分別選取了前40條彈道的打靶結果顯示在圖 4中，靶心為 2 281 m/s，35.51 km.這里滾動時域控制高度跟蹤稍差于LQR方法，但速度控制略優于LQR方法，兩種控制方法效果整體相當;TLC方法的速度和高度落點更集中，略優于其他兩種控制方法的精度.圖5～圖8是加入了初始條件拉偏后的TLC方法對參考軌跡的跟蹤情況.可以看到，TLC方法對于不同參考軌跡也能實現精確跟蹤.

與LQR方法相比，TLC方法具有更寬的適應范圍，其原因在于基于LQR的增益調度方法需要求解Riccati方程，通常難以實時求得最優反饋增益，一般只能根據設計好的參考軌跡離線計算獲得后存儲于制導計算機.為了適應不同的參考軌跡，只能在地面離線生成多組增益，應用時需要根據實際采用的參考軌跡來選用對應的制導反饋增益.由于設計中通常無法考慮所有的非理想情形，因此采用這類制導律設計具有潛在的風險.而TLC方法不依賴于參考軌跡，反饋增益可以符號化表示為參考軌跡的函數，并只需計算簡單的代數式，所需的有限計算量遠小于求解Riccati方程和滾動時域控制方法.此外，TLC方法的跟蹤精度和增益大小與無量綱自然頻率直接相關;對于參考軌跡的不同階段或差別較大的參考軌跡，通過在線改變不同環路自然頻率的數值(同時保證環路間帶寬的分離)即可實現期望的控制效果;另外，TLC方法需要調整的參數數量很少且調整的方向性非常明確.這些區別使得TLC方法不僅可以適應更寬范圍的再入飛行制導任務，而且與軌跡在線生成算法一起將可極大提高再入制導的自主性，適應于應急再入任務規劃、在線任務改變或落點調整等情形.

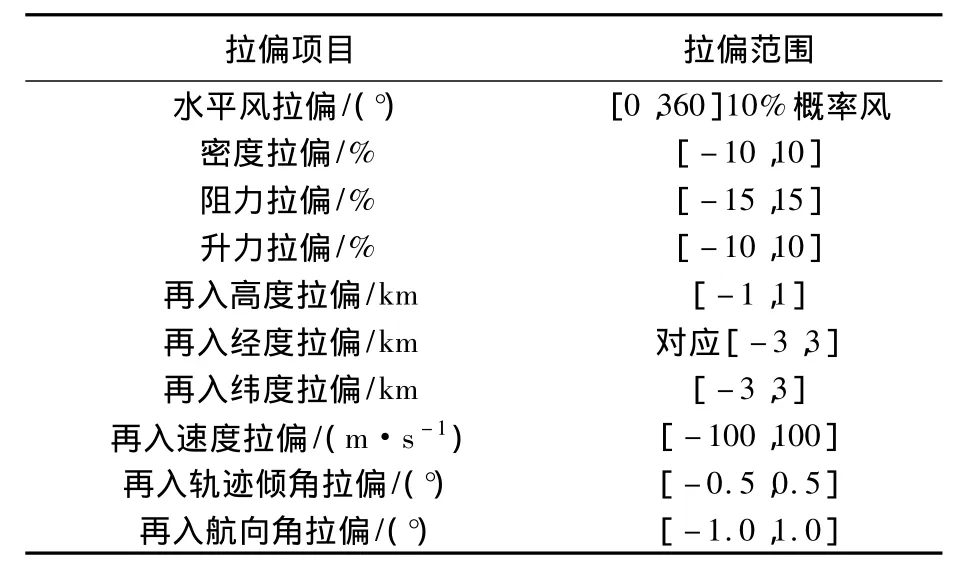
表2 蒙特卡羅拉偏設置Table 2 Monte Carlo dispersion settings

圖4 速度-高度剖面打靶結果Fig.4 Shooting results in velocity-altitude profile

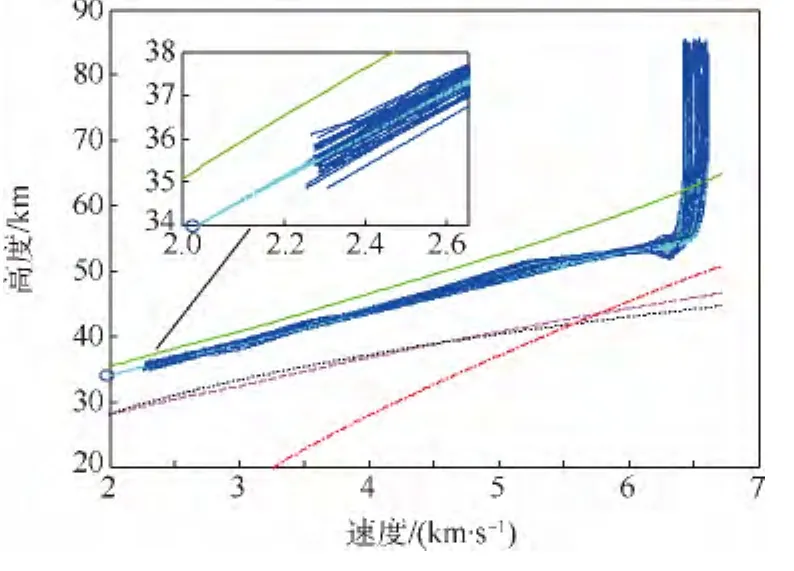
圖5 速度-高度剖面跟蹤Fig.5 Trajectory tracking in velocity-altitude profile

圖6 航程速度剖面的速度跟蹤Fig.6 Velocity tracking in range-velocity profile

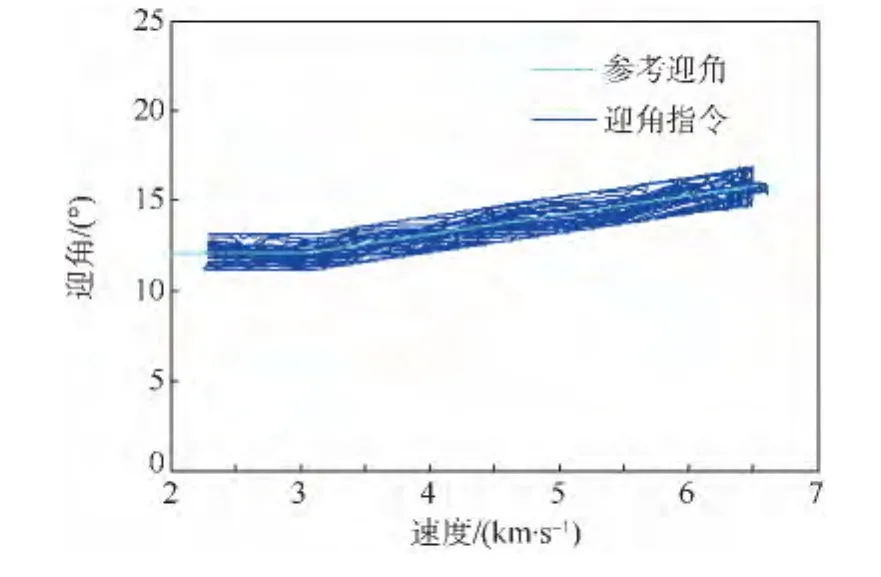
圖7 迎角控制歷程Fig.7 Angle of attack command history

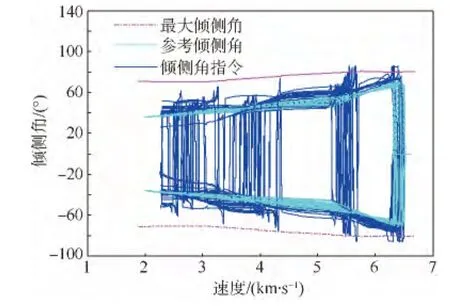
圖8 傾側角控制歷程Fig.8 Bank angle command history

5 結論

本文結合在線軌跡生成算法，將TLC方法應用于制導環的軌跡跟蹤控制中，與現有經典的LQR方法和近似滾動時域控制的仿真對比和分析表明:

1)TLC方法在初始狀態拉偏和擾動情況下也能實現很高的跟蹤精度，體現了方法的有效性和魯棒性.

2)與LQR方法的仿真結果相比，TLC需要調整的參數更少，參數的選取更直觀，對不同參考軌跡有很好的適應性，是一種完全在線的非線性控制方法.與近似滾動時域控制相比，TLC在控制精度略優于前者的情況下計算量顯著減小.

3)在再入軌跡跟蹤制導律中使用TLC控制，可以做到制導環和姿態環控制結構的統一和設計時的一體化;高度、速度、姿態角和姿態角速度的四環路TLC控制策略將更便于制導和控制參數的匹配和實時調整.

因此，本文提出的TLC跟蹤制導策略對于減少制導指令的解算時間，提高制導的自主性、適應性和精度有一定工程意義.

References)

［1］ Lu P.Entry guidance:A unified method［J］.Journal of Guidance，Control，and Dynamics，2014，37(3):713-728.

［2］ Harpold JC，Graves C A Jr.Shuttle entry guidance［J］.Journal of Astronautical Sciences，1979，27(3):239-268.

［3］ Shen Z J，Lu P.Onboard generation of three-dimensional constrained entry trajectories［J］.Journal of Guidance，Control，and Dynamics，2003，26(1):111-121.

［4］ Roenneke A J.Adaptive on-board guidance for entry vehicles［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit.Reston:AIAA Inc.，2001:1-10.

［5］ Saraf A，Leavitt JA，Chen D T，et al.Design and evaluation of an acceleration guidance algorithm for entry［J］.Journal of Spacecraft and Rockets，2004，41(6):986-996.

［6］ Bharadwaj S，Rao A V，Mease K D.Entry trajectory tracking law via feedback linearization［J］.Journal of Guidance，Control，and Dynamics，1998，21(5):726-732.

［7］ Dukeman G A.Profile-following entry guidance using linear quadratic regulator theory［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit.Reston:AIAA Inc.，2002:1-10.

［8］ Lu P.Regulation about time-varying trajectories:Precision entry guidance illustrated［J］.Journal of Guidance，Control，and Dynamics，1999，22(6):784-790.

［9］ Zhu J，Banker BD，Hall CE.X-33 ascent flight controller design by trajectory linearization-a singular perturbation approach［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit.Reston:AIAA Inc.，2000:1-19.

［10］ Vinh N X，Busemann A，Culp R D.Hypersonic and planetary entry flight mechanics［M］.MI，Ann Arbor:University of Michigan Press，1980:26-27.

［11］ Phillips T H.A common aero vehicle(CAV)model，description，and employment guide［R］.［S.l.］:Schafer Corporation for AFRL and AFSPC，2003.

［12］ Zhu J.Nonlinear tracking and decoupling by trajectory linearization［Z］.Lecture Note，Presented at NASA Marshall Space Flight Center.

［13］ Naidu D S，Calise A J.Singular perturbations and time scales in guidance and control of aerospace systems:A survey［J］.Journal of Guidance，Control，and Dynamics，2001，24(6):1057-1078.

［14］ Mease K D.Multiple time-scales in nonlinear flight mechanics:Diagnosis and modeling［J］.Applied Mathematics and Compu-tation，2005，164(2):627-648.

［15］ Lu P，Shen Z J.Unifying treatment to control of nonlinear systems with two timescales［J］.Journal of Guidance，Control，and Dynamics，2002，25(5):975-979.