單-厚盤轉(zhuǎn)子過(guò)兩階臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)分析

劉政，王建軍

(北京航空航天大學(xué) 能源與動(dòng)力工程學(xué)院，北京 100191)

鼓式轉(zhuǎn)子(加強(qiáng)盤鼓式轉(zhuǎn)子)是航空發(fā)動(dòng)機(jī)壓氣機(jī)的基本結(jié)構(gòu)之一，是一類典型的徑向轉(zhuǎn)動(dòng)慣量(Jd)大于軸向轉(zhuǎn)動(dòng)慣量(Jp)轉(zhuǎn)子系統(tǒng).根據(jù)文獻(xiàn)［1］，對(duì)于單-厚盤偏置轉(zhuǎn)子，Jd＞ Jp，即 Jp與Jd之比μ＜1，做正進(jìn)動(dòng)時(shí)系統(tǒng)存在兩階固有頻率.這就是厚盤轉(zhuǎn)子的無(wú)阻尼固有頻率特性.因此，采用厚盤的轉(zhuǎn)子結(jié)構(gòu)件在高工作轉(zhuǎn)速條件下啟動(dòng)或者減速時(shí)，可能穿過(guò)兩個(gè)臨界轉(zhuǎn)速，而且高階臨界轉(zhuǎn)速為厚盤轉(zhuǎn)子特有屬性.

實(shí)際轉(zhuǎn)子結(jié)構(gòu)中，由于加工誤差、鍵槽或者直接采用非圓截面軸等原因，轉(zhuǎn)子系統(tǒng)的彎曲平面剛度在兩個(gè)主方向上存在最大值和最小值，使轉(zhuǎn)子結(jié)構(gòu)呈現(xiàn)出一定的非線性，從而使系統(tǒng)的穩(wěn)定性發(fā)生極大的改變，對(duì)外界激勵(lì)及其變化相當(dāng)敏感.目前，對(duì)非對(duì)稱剛度轉(zhuǎn)子系統(tǒng)的瞬態(tài)動(dòng)力響應(yīng)研究取得了長(zhǎng)足的進(jìn)展.劉占生等［2-3］采用數(shù)值積分，發(fā)現(xiàn)剛度各向異性系數(shù)會(huì)引起系統(tǒng)Hopf分岔、四倍周期分岔和混沌運(yùn)動(dòng)甚至失穩(wěn).Shu、Nandi、Genta等［4-6］則發(fā)展了有限元法對(duì)非對(duì)稱轉(zhuǎn)子的穩(wěn)定性進(jìn)行研究.Darpe、鄒劍、Sekhar等［7-9］針對(duì)裂紋引起的剛度非對(duì)稱分析了轉(zhuǎn)子過(guò)臨界轉(zhuǎn)速時(shí)的瞬態(tài)振動(dòng)，指出裂紋對(duì)轉(zhuǎn)子穩(wěn)定性影響極大.

目前，學(xué)者們都以薄盤轉(zhuǎn)子為研究對(duì)象.鑒于厚盤轉(zhuǎn)子要比薄盤轉(zhuǎn)子多出一個(gè)固有頻率，為研究這類轉(zhuǎn)子通過(guò)臨界轉(zhuǎn)速時(shí)對(duì)不平衡激振力的瞬態(tài)響應(yīng)，采用集中參數(shù)法，簡(jiǎn)化成厚盤轉(zhuǎn)子力學(xué)模型，本文將分別計(jì)算剛度非對(duì)稱單、厚盤轉(zhuǎn)子在定角加速度(φ¨，常數(shù))和定功率(φ·L(φ·)，常數(shù);其中，φ·為定角速度，L(φ·)為軸向外力矩，包括主動(dòng)力矩、阻力矩及重力引起的附加力矩)條件下穿過(guò)兩階臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)，以定角加速度加速的模式分析厚盤轉(zhuǎn)子瞬態(tài)振動(dòng)的基本性質(zhì)，以定功率加速的模式分析厚盤轉(zhuǎn)子與外界能源的非線性耦合效應(yīng)，對(duì)比典型薄盤轉(zhuǎn)子系統(tǒng)，尤其關(guān)注分析厚盤轉(zhuǎn)子過(guò)高階臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)特性，進(jìn)而為帶厚盤轉(zhuǎn)子系統(tǒng)的旋轉(zhuǎn)機(jī)械在設(shè)計(jì)、運(yùn)行、維護(hù)以及故障診斷等工程實(shí)際情況下提供參考.

1 轉(zhuǎn)子的動(dòng)力學(xué)方程

本文采用集中參數(shù)力學(xué)模型如圖1所示.

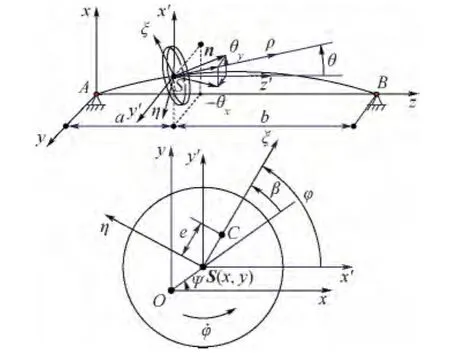
圖1 單盤轉(zhuǎn)子系統(tǒng)集中參數(shù)力學(xué)模型Fig.1 Mechanical model with lumped parameter of single disk rotor system

本模型考慮了剛度不對(duì)稱轉(zhuǎn)子，轉(zhuǎn)動(dòng)慣量的主自由度不一定和剛度的主自由度重合，Jξ、Jη分別為η、ξ方向上的徑向轉(zhuǎn)動(dòng)慣量.根據(jù)文獻(xiàn)［10-11］在靜止坐標(biāo)系中表示的單盤轉(zhuǎn)子系統(tǒng)的動(dòng)能、勢(shì)能及耗散函數(shù)，變換到旋轉(zhuǎn)坐標(biāo)系中，不考慮材料內(nèi)阻尼耗散，根據(jù)Lagrange方程，在旋轉(zhuǎn)坐標(biāo)系下表示的單盤轉(zhuǎn)子系統(tǒng)的動(dòng)力學(xué)方程如式(1a)、式(1b)所示.其中，q為旋轉(zhuǎn)坐標(biāo)系下的廣義力;根據(jù)材料力學(xué)，對(duì)于如圖1所示的單跨轉(zhuǎn)子系統(tǒng)，則有:位移對(duì)力的剛度為kξ，11=3EIξl(a2－ ab+b2)/(a3b3)，kη，11=3EIηl·(a2－ab+b2)/(a3b3);位移對(duì)盤偏角(或彎矩對(duì)力)的剛度為 kξ，12=kξ，21=3EIξl(a －b)/(a2b2)，kη，12=kη，21=3EIηl(a － b)/(a2b2);彎 矩 對(duì) 盤 偏 角 的 剛 度 為 kξ，22=3EIξl/(ab)，kη，22=3EIηl/(ab)，其中:E 為彈性模量;Iξ和 Iη為慣性矩;l=a+b為軸長(zhǎng).

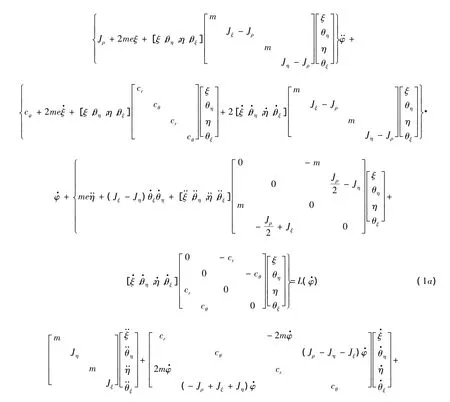
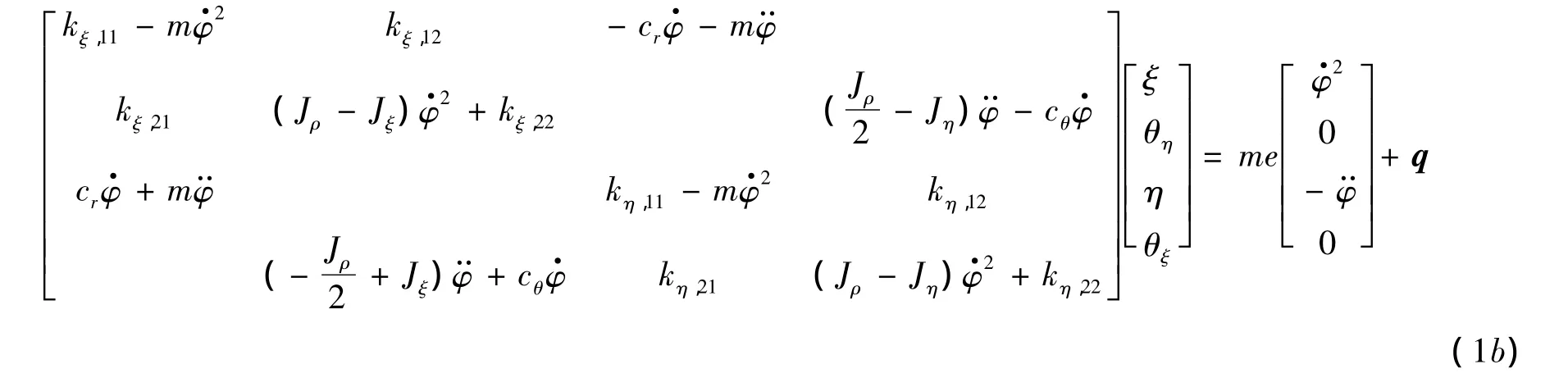
對(duì)方程(1a)和方程(1b)無(wú)量綱化.定義Jd=(Jξ+Jη)/2，d=(Jη－ Jξ)/(Jξ+Jη)，則Jξ=(1 －d)Jd，Jη=(1+d)Jd;同樣地，定義 k .=(kξ.+kη.)/2，κ .=(kξ.－ kη.)/(kξ.+kη.)，則kξ.=(1 － κ .)k .，kη.=(1+ κ .)，k .，.=11，12，22.定義過(guò)直徑轉(zhuǎn)動(dòng)慣量的回轉(zhuǎn)半徑為質(zhì)量;偏心距與徑向回轉(zhuǎn)半徑之比無(wú)量綱位移 Rξ= ξ/e，Rη=η/e;無(wú)量綱角矢量分量分別為 Θη= θη/ν，;靜止固有頻率無(wú)量綱角速度(頻率比)無(wú)量綱角加速度;剛度系數(shù);位移阻尼比偏擺角阻尼比;自轉(zhuǎn)角阻尼比;cr為形心運(yùn)動(dòng)的位移阻尼;cθ為盤偏擺的偏角阻尼;cφ為轉(zhuǎn)子自轉(zhuǎn)阻尼.

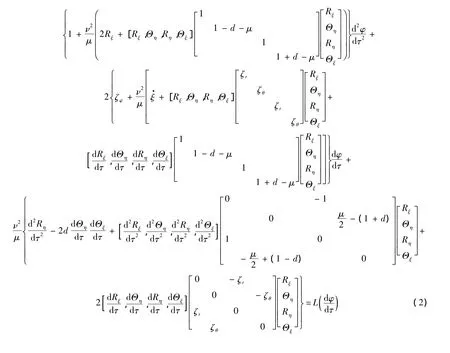
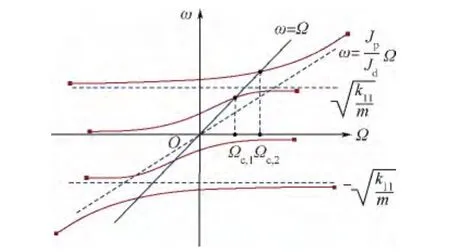
圖2 剛性支承無(wú)阻尼單盤偏置轉(zhuǎn)子渦動(dòng)頻率和自轉(zhuǎn)角速度的關(guān)系曲線(μ＜1)Fig.2 Relationship curves between whirl frequency and angular velocity of undamped single disk rotor with rigid support(μ＜1)

2 厚盤轉(zhuǎn)子定角加速度過(guò)臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)特性

本節(jié)為考察厚盤轉(zhuǎn)子瞬態(tài)的基本振動(dòng)表現(xiàn)，采用定角加速度(φ¨)的直線加速、理想能源模式計(jì)算剛度對(duì)稱厚盤轉(zhuǎn)子的瞬態(tài)響應(yīng).從零轉(zhuǎn)速狀態(tài)線性加速，分別通過(guò)系統(tǒng)的低階臨界轉(zhuǎn)速和高階臨界轉(zhuǎn)速，分析轉(zhuǎn)子軸的動(dòng)撓度放大因子、盤的偏擺角放大因子.由于本文建立方程采用旋轉(zhuǎn)坐標(biāo)系，因此還可以很方便地在旋轉(zhuǎn)坐標(biāo)系下觀察轉(zhuǎn)子形心軌跡，由此判斷系統(tǒng)的振動(dòng)性能和穩(wěn)定性.可見，轉(zhuǎn)子瞬態(tài)響應(yīng)也是分析系統(tǒng)穩(wěn)定性的一個(gè)重要方法.由于加速度恒定，相當(dāng)于轉(zhuǎn)子的自轉(zhuǎn)角自由度退化，成為只含有4個(gè)廣義自由度的系統(tǒng)，方程(2)不參與計(jì)算，只需采用Newmark-β法或四階Runge-Kutta法求解方程(3).為考慮一般單盤轉(zhuǎn)子的回轉(zhuǎn)效應(yīng)，本文設(shè)定盤的位置a=0.4l，l=25rd，rd為盤的半徑;采用不同加速比(α =10－4，10－3，4 × 10－3，10－2)，從靜止開始加速.對(duì)于計(jì)及重力效應(yīng)與否的情況，由于初值不同，將分別予以考慮.

2.1 不計(jì)重力的厚盤轉(zhuǎn)子的瞬態(tài)振動(dòng)特性

不考慮重力效應(yīng)的厚盤轉(zhuǎn)子，則單盤轉(zhuǎn)子初值狀態(tài)為零位移、無(wú)偏角.文獻(xiàn)［12］對(duì)Jeffcott轉(zhuǎn)子過(guò)臨界轉(zhuǎn)速瞬態(tài)振動(dòng)的分析方法，轉(zhuǎn)子軸的無(wú)量綱撓度，則穩(wěn)態(tài)條件下最大臨界撓度δm=1/(2ζr)(同條件下Jeffcott轉(zhuǎn)子發(fā)生共振時(shí)有阻尼最大撓度)，定義動(dòng)撓度放大因子X(jué)=δ/δm;盤的無(wú)量綱偏擺角，與轉(zhuǎn)速以及盤在軸上的位置有關(guān)，因此取偏擺角放大因子為A=Θ/π.一般地，航空發(fā)動(dòng)機(jī)等高精度機(jī)械的偏心距與徑向回轉(zhuǎn)半徑之比在10－3數(shù)量級(jí)范圍內(nèi)，取ν=10－3;偏擺角阻尼比ζθ和自轉(zhuǎn)角阻尼比 ζφ經(jīng)過(guò)無(wú)量綱處理后在10－4數(shù)量級(jí)，取 ζθ=ζφ=2.5 ×10－4，位移阻尼比 ζr=0.02.

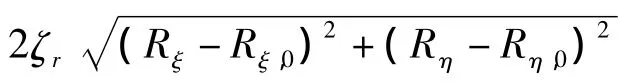
分析圖3(a)～圖3(f)可知，厚盤轉(zhuǎn)子的兩階臨界轉(zhuǎn)速對(duì)應(yīng)于系統(tǒng)的兩階振動(dòng)模態(tài)，低階振型為轉(zhuǎn)子軸的彎曲，高階振型為轉(zhuǎn)子盤的偏轉(zhuǎn).根據(jù)圖3(a)、圖3(c)和圖3(f)表現(xiàn)出的厚盤轉(zhuǎn)子在低階臨界轉(zhuǎn)速的振動(dòng)特征，對(duì)比文獻(xiàn)［1，13-14］關(guān)于薄盤轉(zhuǎn)子過(guò)臨界轉(zhuǎn)速的瞬態(tài)動(dòng)力學(xué)特征，厚盤轉(zhuǎn)子服從柔性轉(zhuǎn)子加速通過(guò)臨界轉(zhuǎn)速的一般振動(dòng)規(guī)律和結(jié)論，不再詳述.需要指出的是，薄盤轉(zhuǎn)子過(guò)臨界轉(zhuǎn)速時(shí)，其振動(dòng)峰值在ω＞ωn位置處出現(xiàn)，即振動(dòng)峰值應(yīng)在橫坐標(biāo)大于1時(shí)出現(xiàn)，于厚盤轉(zhuǎn)子而言，以圖 3(a)為例，當(dāng) α =10－4和 10－3時(shí)，振動(dòng)峰值在ω＜ωn時(shí)出現(xiàn)，這是由于厚盤轉(zhuǎn)子回轉(zhuǎn)效應(yīng)遠(yuǎn)遠(yuǎn)明顯于薄盤轉(zhuǎn)子，造成系統(tǒng)Ωc，1＜ωn，這在圖2中十分形象;另外，在低轉(zhuǎn)速情況下，轉(zhuǎn)子軸的撓曲和盤的偏擺角是同步的，兩者隨時(shí)間的變化規(guī)律相同.

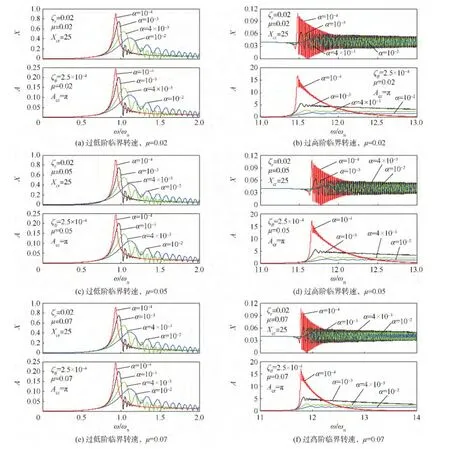
圖3 厚盤轉(zhuǎn)子過(guò)低階及高階臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)特性曲線(μ=0.02，0.05，0.07)Fig.3 Transient vibration curves of thick-disk rotor crossing lower and higher order critical speed(μ =0.02，0.05，0.07)

根據(jù)圖3(b)、圖3(e)和圖4，厚盤轉(zhuǎn)子在高階臨界轉(zhuǎn)速對(duì)應(yīng)于高階模態(tài)，對(duì)不平衡力的瞬態(tài)響應(yīng)與低階臨界轉(zhuǎn)速有很大的不同.

1)在高速條件下，盤的偏轉(zhuǎn)比軸的彎曲對(duì)激勵(lì)要敏感得多.通過(guò)高階臨界轉(zhuǎn)速時(shí)，主振型為盤的偏轉(zhuǎn);而且由于當(dāng)?shù)剞D(zhuǎn)速很大，回轉(zhuǎn)效應(yīng)對(duì)轉(zhuǎn)子影響極其顯著.

2)通過(guò)高階臨界轉(zhuǎn)速時(shí)，產(chǎn)生的瞬態(tài)振動(dòng)響應(yīng)非常迅速，在極小的時(shí)間內(nèi)即達(dá)到最大值，尤其是小加速度轉(zhuǎn)子更為明顯.

3)通過(guò)高階臨界轉(zhuǎn)速后，由共振激起的按系統(tǒng)高階固有頻率的自由振動(dòng)和在當(dāng)?shù)剞D(zhuǎn)速頻率下的強(qiáng)迫振動(dòng)合成很激烈的高頻振蕩.

4)通過(guò)高階轉(zhuǎn)速后，線性加速的系統(tǒng)仍然具有穩(wěn)定性，振動(dòng)逐漸衰減.這就是柔性轉(zhuǎn)子的自定心效應(yīng).但是，小加速度的轉(zhuǎn)子呈指數(shù)衰減，大加速度幾乎呈線性衰減.

5)無(wú)論低階還是高階，過(guò)臨界轉(zhuǎn)速時(shí)的自轉(zhuǎn)角加速度對(duì)轉(zhuǎn)子的瞬態(tài)振動(dòng)影響很大;加速度越大，慣性力越大，過(guò)臨界轉(zhuǎn)速時(shí)對(duì)振動(dòng)有一定的抑制作用，產(chǎn)生的瞬態(tài)振動(dòng)振幅越小;但同時(shí)，發(fā)生瞬態(tài)共振后，加速度越大，阻尼對(duì)系統(tǒng)的影響就相對(duì)較弱，因此衰減也越來(lái)越慢.這在過(guò)高階臨界轉(zhuǎn)速后的振動(dòng)中十分明顯.

反過(guò)來(lái)，根據(jù)高階共振發(fā)生的轉(zhuǎn)速位置可見，μ值越小，高階臨界轉(zhuǎn)速越靠前;當(dāng)μ大到一定程度時(shí)，實(shí)際轉(zhuǎn)子由于能量有限，很難達(dá)到高階臨界轉(zhuǎn)速;當(dāng)μ值大于1時(shí)，轉(zhuǎn)子失去高階臨界轉(zhuǎn)速;當(dāng)μ=2時(shí)，即為典型的薄盤轉(zhuǎn)子.

由于旋轉(zhuǎn)坐標(biāo)系不考慮轉(zhuǎn)子自轉(zhuǎn)對(duì)形心運(yùn)動(dòng)的干擾，因此可以在旋轉(zhuǎn)坐標(biāo)系中清晰地觀察到形心運(yùn)動(dòng)軌跡，這在單轉(zhuǎn)子系統(tǒng)中對(duì)比固定坐標(biāo)系是一個(gè)較為明顯的優(yōu)點(diǎn).以μ=0.05為例，著重分析穿過(guò)兩階臨界轉(zhuǎn)速過(guò)程中的瞬態(tài)振動(dòng)，以此判斷轉(zhuǎn)子的穩(wěn)定性.圖4和圖5給出了厚盤轉(zhuǎn)子形心加速過(guò)程中各個(gè)階段在旋轉(zhuǎn)坐標(biāo)系中的軌跡，圖6(a)和圖6(b)給出了轉(zhuǎn)子穿過(guò)高低轉(zhuǎn)速時(shí)盤的偏擺角矢尖(盤的單位外法矢量尖)在旋轉(zhuǎn)坐標(biāo)系中的軌跡，其中圖5(a)和圖6(a)為過(guò)低階臨界轉(zhuǎn)速的軌跡，從零初始條件開始到穩(wěn)定區(qū)結(jié)束，圖5(b)和圖6(b)為過(guò)高階臨界轉(zhuǎn)速的軌跡，從穩(wěn)定區(qū)開始到緩慢衰減結(jié)束(其中，加速比α=10－4的轉(zhuǎn)子已經(jīng)進(jìn)入高轉(zhuǎn)速穩(wěn)定區(qū)).

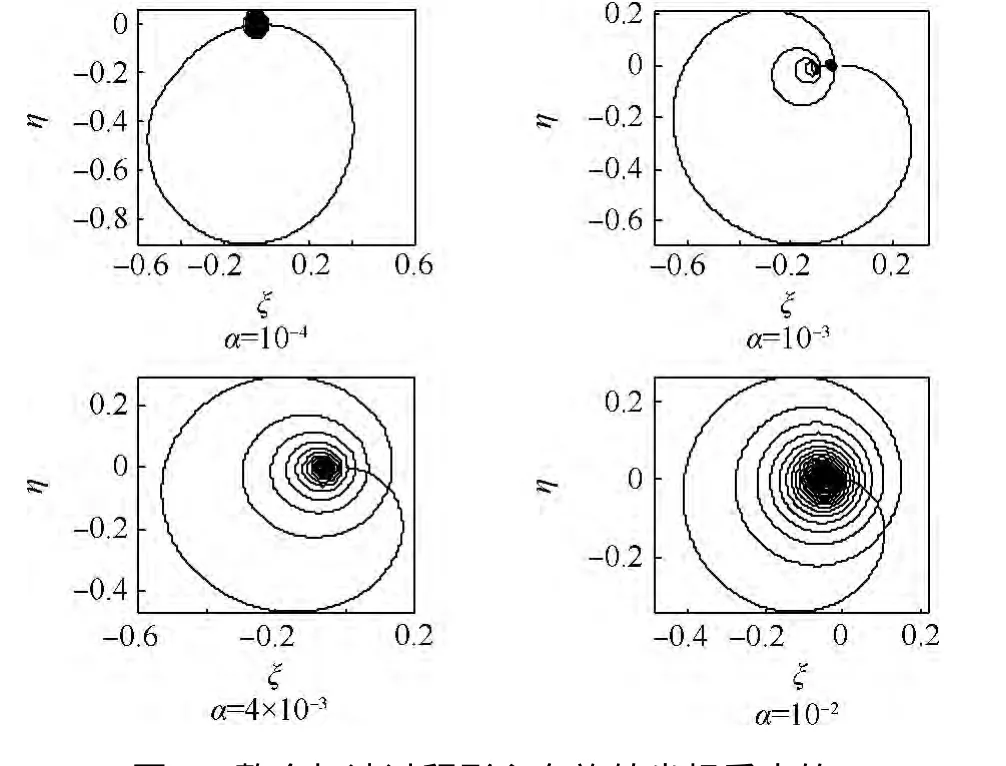
圖4 整個(gè)加速過(guò)程形心在旋轉(zhuǎn)坐標(biāo)系中的軌跡(μ =0.05)Fig.4 Trajectories of centroid in whole speed-up process in rotating coordinate(μ =0.05)

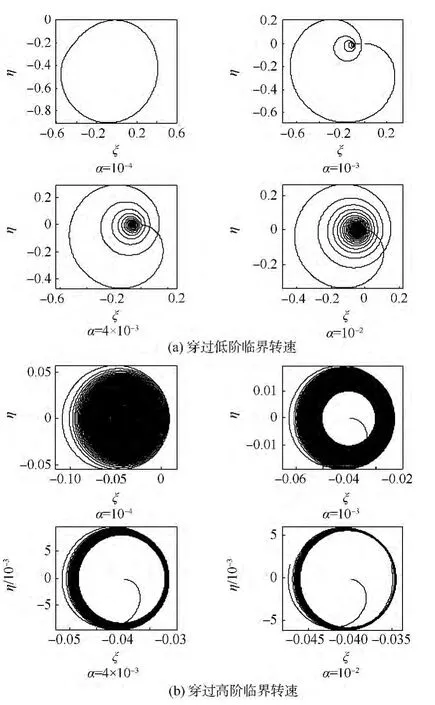
圖5 穿過(guò)低階及高階臨界轉(zhuǎn)速時(shí)形心在旋轉(zhuǎn)坐標(biāo)系中的軌跡(μ=0.05)Fig.5 Trajectories of centroid crossing lower and higher order critical speed in rotating coordinate(μ =0.05)

根據(jù)圖5(a)和圖6(a)可見，在旋轉(zhuǎn)坐標(biāo)系中，低轉(zhuǎn)速時(shí)轉(zhuǎn)子形心的軌跡和盤偏擺角矢尖的軌跡形狀幾乎完全相同.這也說(shuō)明，低轉(zhuǎn)速情況下軸的彎曲和盤的偏轉(zhuǎn)是同步的.注意坐標(biāo)的數(shù)量級(jí)，穿過(guò)低階臨界轉(zhuǎn)速時(shí)，軸的彎曲振動(dòng)很強(qiáng)烈，而盤的偏擺比較微弱.

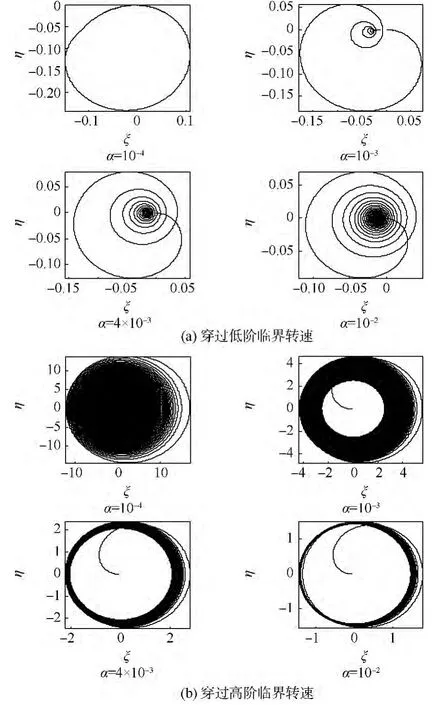
圖6 穿過(guò)低階及高階臨界轉(zhuǎn)速時(shí)盤偏角矢尖在旋轉(zhuǎn)坐標(biāo)系中的軌跡(μ=0.05)Fig.6 Trajectories of declination angle vector tip of disk crossing lower and higher order critical speed in rotating coordinate(μ =0.05)

當(dāng)轉(zhuǎn)子超過(guò)低階臨界轉(zhuǎn)速后，形心漸進(jìn)趨近于旋轉(zhuǎn)坐標(biāo)系中的點(diǎn)(－2ζ，0)，表現(xiàn)出的動(dòng)態(tài)螺旋運(yùn)動(dòng)過(guò)程(圖3為加速過(guò)程，方向順時(shí)針).在低階和高階臨界轉(zhuǎn)速之間，剛度對(duì)稱的厚盤轉(zhuǎn)子有一段很長(zhǎng)的穩(wěn)定轉(zhuǎn)速區(qū)，理論上，由于自定心效應(yīng)，質(zhì)心將穩(wěn)定于(0，0)點(diǎn)，形心穩(wěn)定于(－2ζ，0).盤偏角矢尖也服從相同的規(guī)律，但是在到達(dá)高階臨界轉(zhuǎn)速之前，軌跡范圍始終處于一個(gè)很小的數(shù)量級(jí)上.

當(dāng)轉(zhuǎn)子穿過(guò)高階轉(zhuǎn)速時(shí)，盤突然偏擺得很劇烈，振動(dòng)幅值是穩(wěn)定轉(zhuǎn)速區(qū)的上百倍，矢尖在空間高頻偏轉(zhuǎn).不同加速度由于衰減程度不同，形成的軌跡略有不同，但是服從相同的規(guī)律.由圖5(b)的α=10－4分圖及圖6(b)的α=10－4分圖可知，在通過(guò)高階臨界轉(zhuǎn)速之后，轉(zhuǎn)子穩(wěn)定在高轉(zhuǎn)速區(qū)，矢尖又在旋轉(zhuǎn)坐標(biāo)系中穩(wěn)定于一點(diǎn).形心則過(guò)高階臨界轉(zhuǎn)速表現(xiàn)出微小的高頻波動(dòng)，恰好共振時(shí)在旋轉(zhuǎn)坐標(biāo)系中的速度方向(即從穩(wěn)定區(qū)進(jìn)入高階臨界轉(zhuǎn)速時(shí)軌跡的切線方向)與盤的矢尖在旋轉(zhuǎn)非慣性參考系中的速度方向成180°，除此之外和矢尖軌跡的變化規(guī)律相同.

由以上轉(zhuǎn)子的瞬態(tài)振動(dòng)特性分析可知，做正進(jìn)動(dòng)的單、厚盤轉(zhuǎn)子系統(tǒng)有兩階模態(tài)，其中低階振型為軸的彎曲，高階振型為盤的偏擺.在穿過(guò)兩階臨界轉(zhuǎn)速時(shí)，發(fā)生由按系統(tǒng)固有頻率的自由振動(dòng)和在當(dāng)?shù)剞D(zhuǎn)速頻率下的強(qiáng)迫振動(dòng)合成的瞬態(tài)振動(dòng).在有阻尼系統(tǒng)中，單、厚盤轉(zhuǎn)子系統(tǒng)存在穩(wěn)定轉(zhuǎn)速區(qū).

2.2 考慮重力的厚盤轉(zhuǎn)子瞬態(tài)振動(dòng)特性

本節(jié)在2.1節(jié)基礎(chǔ)上，考慮重力對(duì)單、厚盤轉(zhuǎn)子過(guò)臨界轉(zhuǎn)速時(shí)的瞬態(tài)振動(dòng)特性的影響.在考慮重力時(shí)，轉(zhuǎn)子在零轉(zhuǎn)速時(shí)已經(jīng)具有初始彎曲和偏擺角.根據(jù)方程(3)，無(wú)量綱重力，在100數(shù)量級(jí)左右，取 G=1.0;另外，根據(jù)文獻(xiàn)［13］，存在偏心的轉(zhuǎn)子還受重力對(duì)自轉(zhuǎn)軸線的矩－mge cosφ，使得轉(zhuǎn)子在設(shè)定的旋轉(zhuǎn)角加速度附近波動(dòng)，同時(shí)存在一個(gè)切向慣性力，在固定坐標(biāo)系中以2倍自轉(zhuǎn)角頻率影響系統(tǒng)的穩(wěn)態(tài)和瞬態(tài)響應(yīng)，這就是重力的副臨界效應(yīng).因此，受無(wú)量綱重力作用的轉(zhuǎn)子自轉(zhuǎn)角加速度為

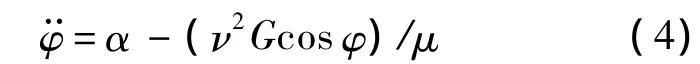
Q=［－G sinφ，0，－G cosφ，0］T為廣義力，r0=K－1［0，0，－G，0］T為初值(靜平衡位移和偏擺角)，K為轉(zhuǎn)子的剛度矩陣.

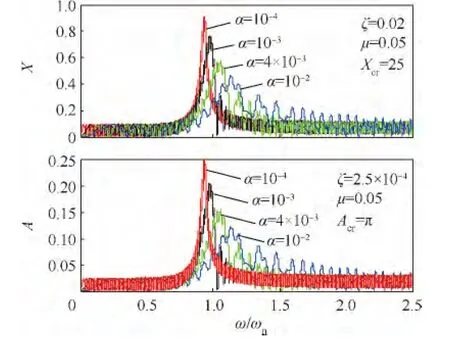
圖7 計(jì)重力厚盤轉(zhuǎn)子過(guò)低階臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)曲線Fig.7 Transient vibration curves of thick-disk rotor crossing lower order critical speed with gravity taken into account

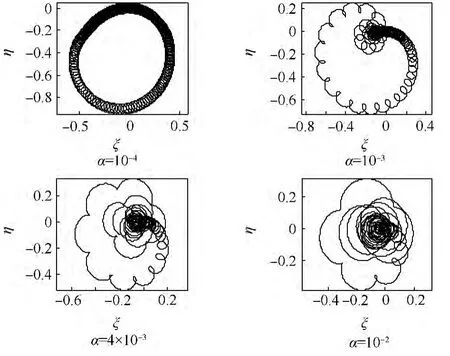
圖8 計(jì)重力過(guò)低階臨界轉(zhuǎn)速的厚盤轉(zhuǎn)子形心在旋轉(zhuǎn)坐標(biāo)中的軌跡Fig.8 Trajectories of thick-disk centroid crossing lower order critical speed in rotating coordinate with gravity taken into account

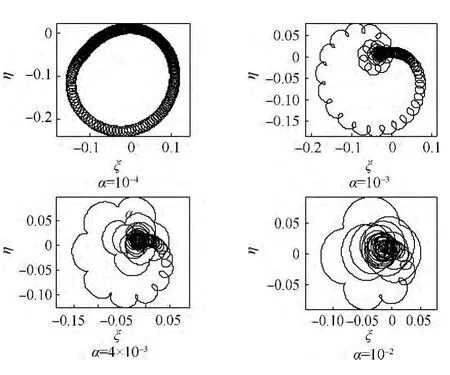
圖9 計(jì)重力過(guò)低階臨界轉(zhuǎn)速時(shí)盤偏角矢尖在旋轉(zhuǎn)坐標(biāo)中的軌跡Fig.9 Trajectories of declination angle vector tip of disk crossing lower order critical speed in rotating coordinate with gravity taken into account

以μ=0.05的轉(zhuǎn)子為例，分析厚盤轉(zhuǎn)子系統(tǒng)受重力與不平衡力作用后的瞬態(tài)振動(dòng)表現(xiàn).圖7～圖9分別給出了轉(zhuǎn)子線性加速穿過(guò)低階臨界轉(zhuǎn)速時(shí)的軸的動(dòng)撓度和盤的偏擺角瞬態(tài)振動(dòng)曲線、形心在旋轉(zhuǎn)坐標(biāo)系中的軌跡和盤偏角矢尖(盤的單位外法矢量尖)在旋轉(zhuǎn)坐標(biāo)系中的軌跡.

對(duì)于式(4)中第2項(xiàng)，由于ν值很小，相較于第1項(xiàng)可以忽略，可見對(duì)對(duì)稱厚盤轉(zhuǎn)子而言重力對(duì)轉(zhuǎn)速的影響很小.由于方程(3)是線性的，根據(jù)疊加原理可知，轉(zhuǎn)子的瞬態(tài)振動(dòng)是由不平衡力和重力疊加激勵(lì)的結(jié)果，因此對(duì)比圖3(c)，在圖7表示的軸的動(dòng)撓度和盤偏角出現(xiàn)了疊加在圖3(c)所示的曲線上的次諧波振動(dòng).厚盤轉(zhuǎn)子過(guò)低階臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)規(guī)律與普通單盤轉(zhuǎn)子相同，這些理論已經(jīng)發(fā)展成熟，本文不再討論.但是，受重力作用的非對(duì)稱轉(zhuǎn)子的瞬態(tài)振動(dòng)與對(duì)稱轉(zhuǎn)子有很大的不同，不僅存在副臨界轉(zhuǎn)速［13］，還可能引起非線性振動(dòng)［15-16］.

3 剛度非對(duì)稱厚盤轉(zhuǎn)子瞬態(tài)振動(dòng)特性

鑒于國(guó)內(nèi)外學(xué)者對(duì)剛度非對(duì)稱轉(zhuǎn)子已有研究，本節(jié)主要以 μ=0.05、剛度非對(duì)稱系數(shù) κ=0.03的單、厚盤轉(zhuǎn)子為例，說(shuō)明剛度非對(duì)稱厚盤轉(zhuǎn)子過(guò)臨界轉(zhuǎn)速時(shí)瞬態(tài)振動(dòng)的基本特征，尤其是薄盤轉(zhuǎn)子所不具有的高階模態(tài).

采用2.1節(jié)關(guān)于對(duì)稱厚盤轉(zhuǎn)子的研究方法，設(shè)定加速比 α =10－4，10－3，4 × 10－3，10－2，不考慮重力，從零轉(zhuǎn)速、零位移、零偏角的初始條件開始，計(jì)算轉(zhuǎn)子 μ=0.05、κ=0.03的厚盤轉(zhuǎn)子過(guò)低階、高階臨界轉(zhuǎn)速時(shí)的軸的動(dòng)撓度和盤偏角，如圖10(a)和圖10(b)所示.圖11和圖12分別給出了過(guò)低階、高階臨界轉(zhuǎn)速形心軌跡和盤偏角矢尖軌跡.

圖10 不對(duì)稱厚盤轉(zhuǎn)子過(guò)低階及高階臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)曲線Fig.10 Transient vibration curves of asymmetric thick-disk rotor crossing lower and higher order critical speed

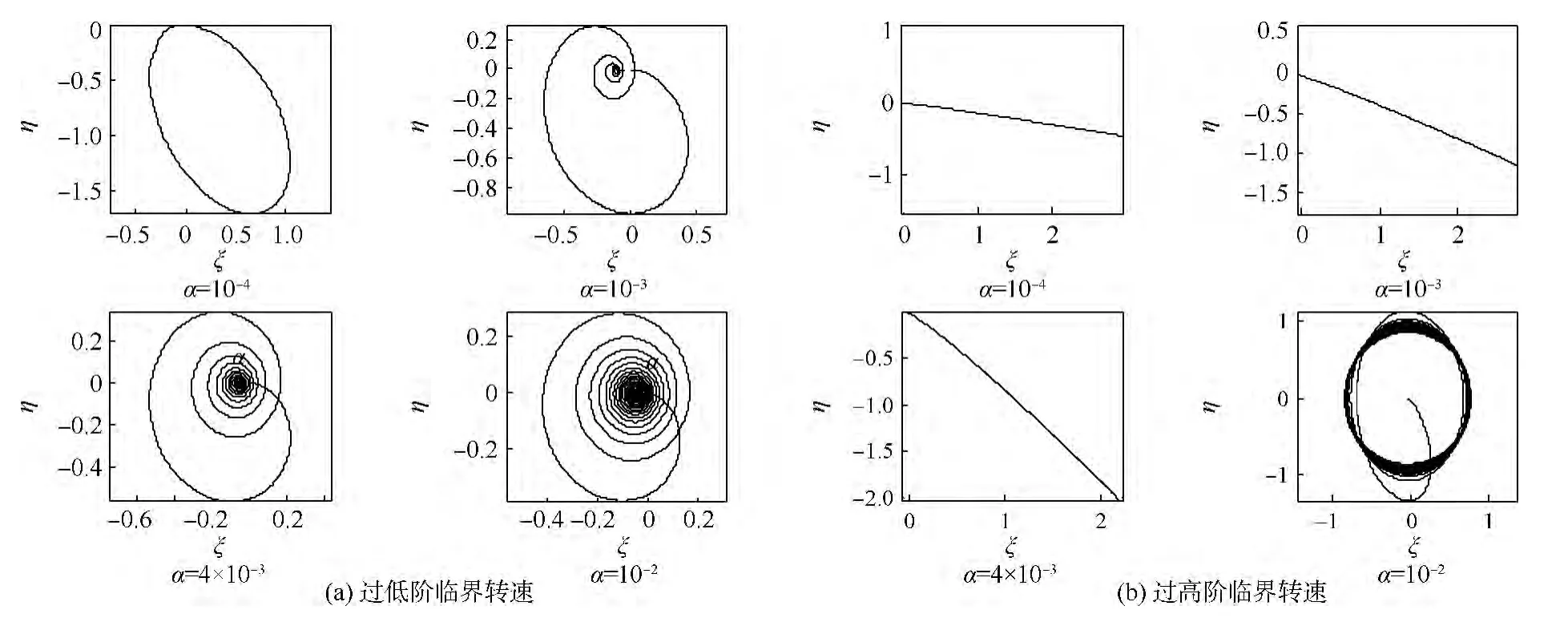
圖11 不對(duì)稱厚盤轉(zhuǎn)子過(guò)低階及高階臨界轉(zhuǎn)速形心軌跡Fig.11 Trajectories of centroid of asymmetric thick-disk rotor crossing lower and higher order critical speed

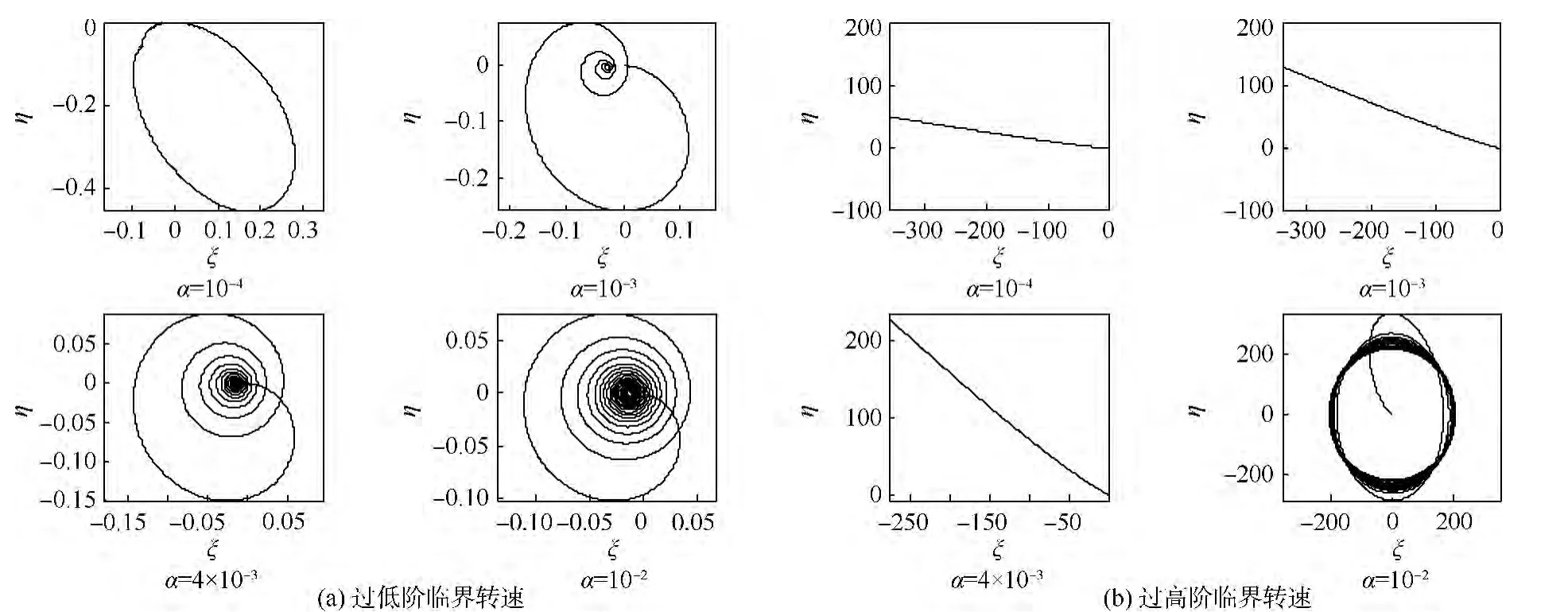
圖12 不對(duì)稱厚盤轉(zhuǎn)子過(guò)低階及高階臨界轉(zhuǎn)速盤偏角矢尖軌跡Fig.12 Trajectories of declination angle vector tip of disk of asymmetric thick-disk rotor crossing lower and higher order critical speed

對(duì)比圖10(a)和圖3(c)可得，在低階臨界轉(zhuǎn)速附近，由于剛度的不對(duì)稱性，瞬態(tài)振動(dòng)的幅值顯著增大，在旋轉(zhuǎn)坐標(biāo)系中的形心軌跡呈橢圓形;過(guò)低階臨界轉(zhuǎn)速后，轉(zhuǎn)子仍然能恢復(fù)穩(wěn)定，保持在較小的振幅.

然而，當(dāng)厚盤轉(zhuǎn)子過(guò)高階臨界轉(zhuǎn)速時(shí)，由主振型引起的盤的偏擺急劇增大，軸的動(dòng)撓度隨之發(fā)散，系統(tǒng)若以小加速度加速時(shí)在高階臨界轉(zhuǎn)速點(diǎn)上迅速失穩(wěn)，大加速度則能保持有限振幅，穿過(guò)臨界轉(zhuǎn)速后振動(dòng)發(fā)生近似線性的衰減.

4 厚盤轉(zhuǎn)子定功率過(guò)臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)特性

如第2節(jié)所述，線性加速度缺少一個(gè)自由度，并不能考慮外界能量與轉(zhuǎn)子系統(tǒng)的相互作用.本節(jié)針對(duì)具有非對(duì)稱剛度的厚盤轉(zhuǎn)子結(jié)構(gòu)考慮一種更接近實(shí)際的工況:定功率的有限能量模式.

當(dāng)轉(zhuǎn)子工作于某一穩(wěn)定轉(zhuǎn)速時(shí)，系統(tǒng)的無(wú)量綱功率為

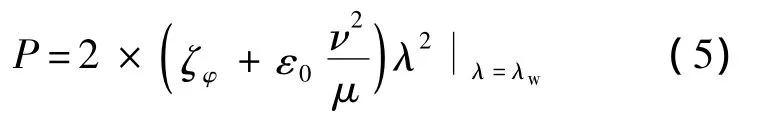
ε0為一修正值，本文取為0.1，則

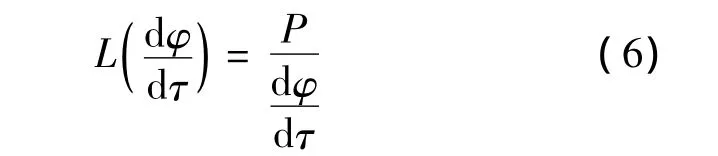
式(5)和式(6)代入方程(2)，采用四階 Runge-Kutta法聯(lián)立求解方程(2)和方程(3).設(shè)定工作轉(zhuǎn)速在低、高階臨界轉(zhuǎn)速附近，考察厚盤轉(zhuǎn)子在定功率有限能量模式下瞬態(tài)振動(dòng)的基本特性.下面計(jì)算單、厚盤轉(zhuǎn)子過(guò)低階臨界轉(zhuǎn)速時(shí)的瞬態(tài)振動(dòng)，其中λw=0.8表示工作轉(zhuǎn)速為亞臨界轉(zhuǎn)速，λw=1.2，1.6，2.0 表示工作轉(zhuǎn)速為超臨界轉(zhuǎn)速，在圖13～圖21中給出了對(duì)稱厚盤轉(zhuǎn)子和非對(duì)稱(κ =0.05，0.07)厚盤轉(zhuǎn)子時(shí)域、頻域瞬態(tài)振動(dòng)以及旋轉(zhuǎn)系中形心軌跡.

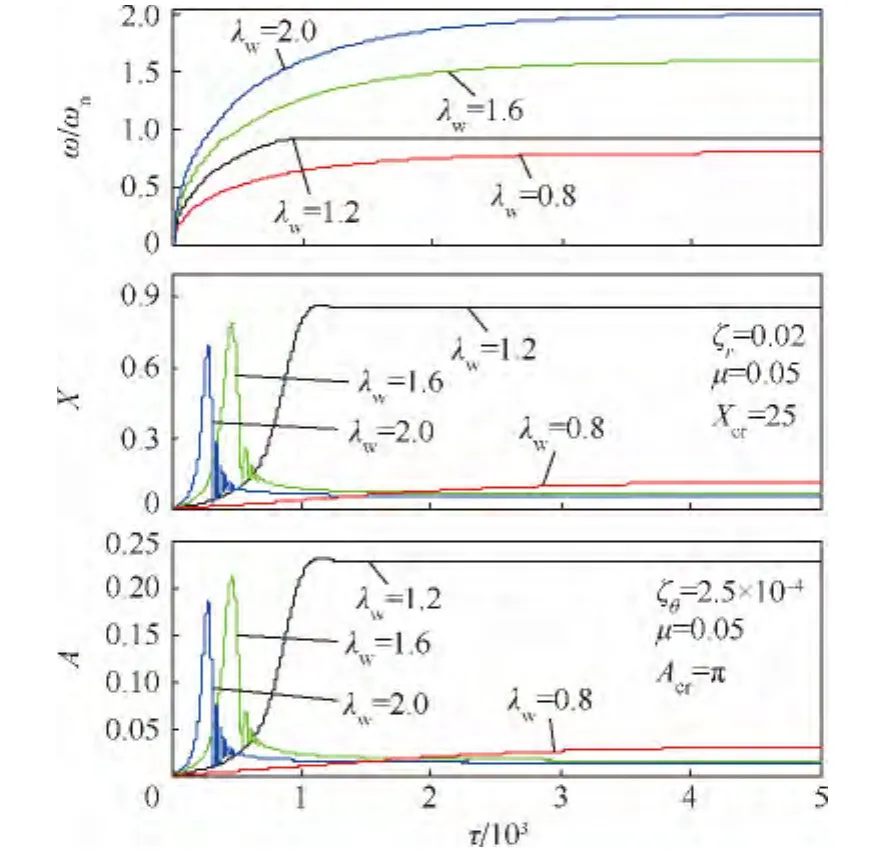
圖13 低階臨界轉(zhuǎn)速附近工作的對(duì)稱厚盤轉(zhuǎn)子隨時(shí)間的瞬態(tài)振動(dòng)曲線Fig.13 Transient vibration curves over time of symmetric thick-disk rotor with working speed near lower order critical speed

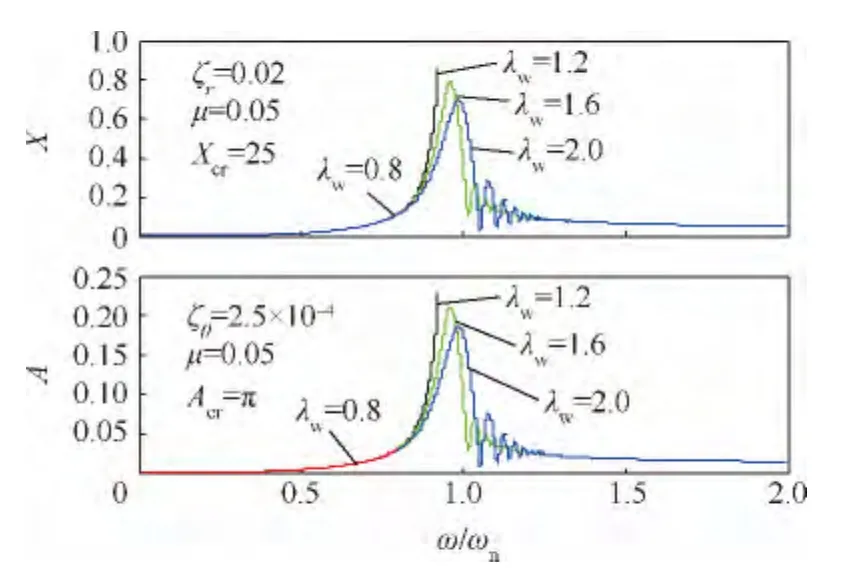
圖14 低階臨界轉(zhuǎn)速附近工作的對(duì)稱厚盤轉(zhuǎn)子隨轉(zhuǎn)速的瞬態(tài)振動(dòng)曲線Fig.14 Transient vibration curves over speed of symmetric thick-disk rotor with working speed near lower order critical speed

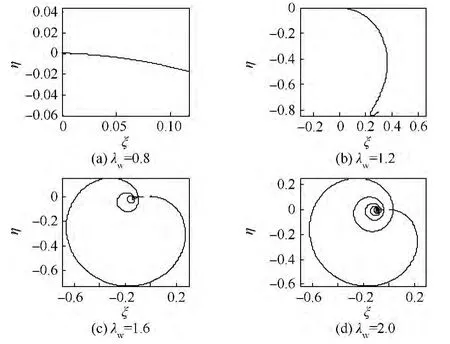
圖15 低階臨界轉(zhuǎn)速附近工作的對(duì)稱厚盤轉(zhuǎn)子形心軌跡Fig.15 Trajectories of centroid of symmetric thick-disk rotor with working speed near lower order critical speed

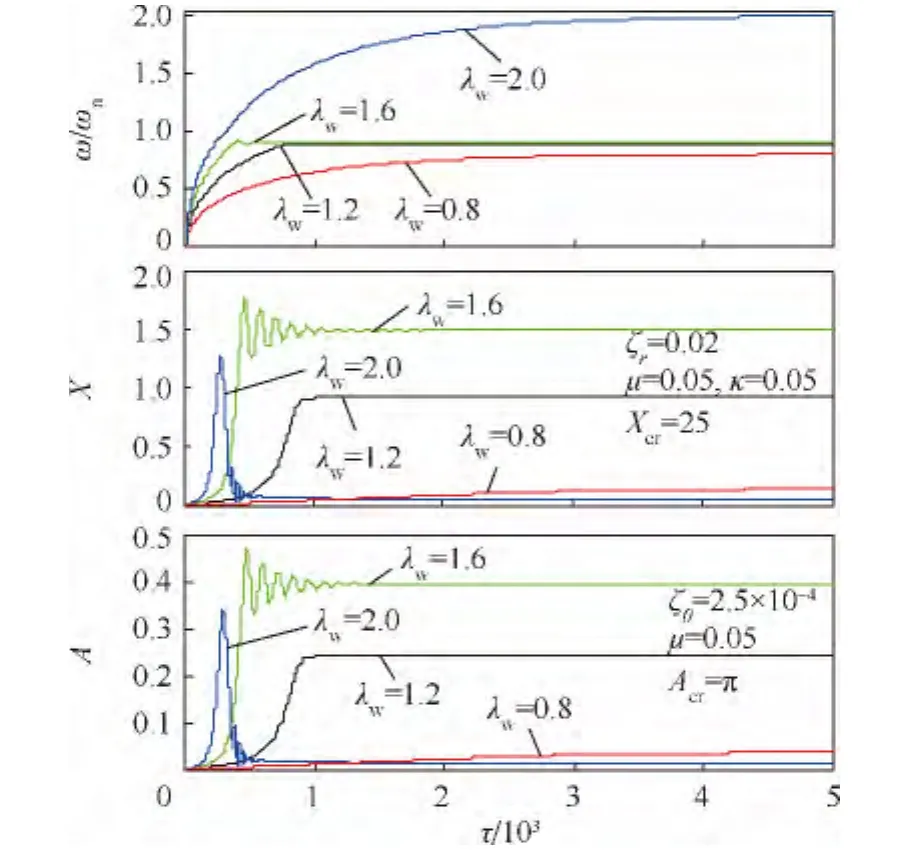
圖16 低階臨界轉(zhuǎn)速附近工作的非對(duì)稱(κ=0.05)厚盤轉(zhuǎn)子隨時(shí)間的瞬態(tài)振動(dòng)曲線Fig.16 Transient vibration curves over time of asymmetric thick-disk rotor(κ =0.05)with working speed near lower order critical speed

圖17 低階臨界轉(zhuǎn)速附近工作的非對(duì)稱(κ=0.05)厚盤轉(zhuǎn)子隨轉(zhuǎn)速的瞬態(tài)振動(dòng)曲線Fig.17 Transient vibration curves over speed of asymmetric thick-disk rotor(κ =0.05)with working speed near lower order critical speed

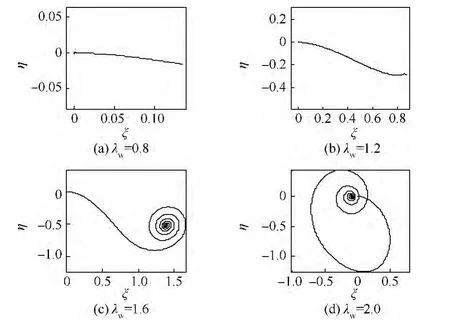
圖18 非對(duì)稱(κ=0.05)厚盤轉(zhuǎn)子在低階臨界轉(zhuǎn)速附近振動(dòng)的形心軌跡Fig.18 Trajectories of centroid of asymmetric thick-disk rotor(κ =0.05)with working speed near lower order critical speed

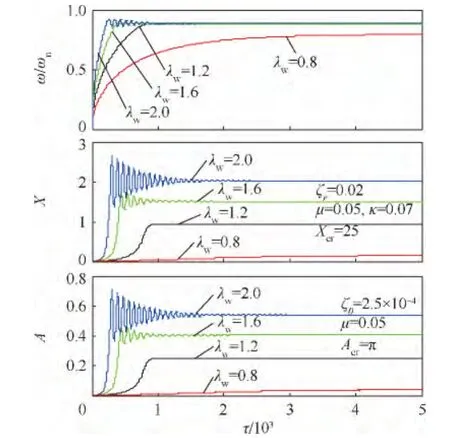
圖19 低階臨界轉(zhuǎn)速附近工作的非對(duì)稱(κ=0.07)厚盤轉(zhuǎn)子隨時(shí)間的瞬態(tài)振動(dòng)曲線Fig.19 Transient vibration curves over time of asymmetric thick-disk rotor(κ =0.07)with working speed near lower order critical speed

圖20 低階臨界轉(zhuǎn)速附近工作的非對(duì)稱(κ=0.07)厚盤轉(zhuǎn)子隨時(shí)間的瞬態(tài)振動(dòng)曲線Fig.20 Transient vibration curves over speed of asymmetric thick-disk rotor(κ =0.07)with working speed near lower order critical speed

圖21 低階臨界轉(zhuǎn)速附近工作的非對(duì)稱(κ=0.07)厚盤轉(zhuǎn)子瞬態(tài)振動(dòng)的形心軌跡Fig.21 Trajectories of centroid of asymmetric thick-disk rotor(κ =0.07)with working speed near lower order critical speed

根據(jù)λw=0.8的計(jì)算結(jié)果可知，若工作轉(zhuǎn)速低于臨界轉(zhuǎn)速，顯然轉(zhuǎn)子的角速度是不能穿過(guò)臨界轉(zhuǎn)速的，到達(dá)工作轉(zhuǎn)速后即發(fā)生穩(wěn)態(tài)振動(dòng).因此，以亞臨界轉(zhuǎn)速工作的厚盤轉(zhuǎn)子不會(huì)出現(xiàn)振幅大幅增加的非線性振動(dòng).由圖13、圖16和圖19可見，當(dāng)工作轉(zhuǎn)速高于臨界轉(zhuǎn)速，若不發(fā)生過(guò)臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)，則能維持在超臨界轉(zhuǎn)速下運(yùn)行，振動(dòng)幅值不會(huì)劇增.但是，如果外界能源不能向厚盤轉(zhuǎn)子系統(tǒng)提供足夠穿越臨界轉(zhuǎn)速的能量，自轉(zhuǎn)轉(zhuǎn)速會(huì)隨著軸的動(dòng)撓度和盤的偏擺角的瞬態(tài)振動(dòng)而出現(xiàn)波動(dòng)，造成能量耦合，從而激起系統(tǒng)的非線性振動(dòng)，發(fā)生“失速”現(xiàn)象.這是定功率的有限能量模式區(qū)別于定角加速度的理想能源模式最大的特點(diǎn).進(jìn)一步，發(fā)生“失速”的轉(zhuǎn)速，對(duì)同一系統(tǒng)是一個(gè)定值，低于臨界轉(zhuǎn)速;這時(shí)，功率大小只造成非線性瞬態(tài)振動(dòng)的幅值變化，而不能使轉(zhuǎn)子轉(zhuǎn)速繼續(xù)上升，除非有足夠大的功率克服振動(dòng)引起的阻力矩.“失速”后，外界能源輸入的能量被轉(zhuǎn)子系統(tǒng)耗散和轉(zhuǎn)化為勢(shì)能存儲(chǔ)起來(lái).

圖22～圖25分別給出了κ=0的對(duì)稱厚盤轉(zhuǎn)子 λw=11.4，11.8，12.4，13.0 和 κ =0.03 的非對(duì)稱厚盤轉(zhuǎn)子以λw=20，25，30，35過(guò)高階臨界轉(zhuǎn)速隨時(shí)間變化的瞬態(tài)振動(dòng)曲線和盤偏角矢尖(以盤的偏擺表征高階振動(dòng))在旋轉(zhuǎn)坐標(biāo)系中的軌跡.可以發(fā)現(xiàn)，厚盤轉(zhuǎn)子在高階臨界轉(zhuǎn)速附近也存在“失速”現(xiàn)象，盤偏角矢尖軌跡出現(xiàn)分叉，尤其對(duì)非對(duì)稱轉(zhuǎn)子由于非線性振動(dòng)，要求極高的功率才能順利通過(guò)高階臨界轉(zhuǎn)速.因此，實(shí)際工程中的厚盤轉(zhuǎn)子結(jié)構(gòu)是很難在高階臨界轉(zhuǎn)速之上運(yùn)行.若外界功率足夠大，厚盤轉(zhuǎn)子通過(guò)臨界轉(zhuǎn)速后，瞬態(tài)振動(dòng)衰減，系統(tǒng)仍能保持穩(wěn)定，這在以盤的偏擺為高階振型的振動(dòng)上十分明顯.

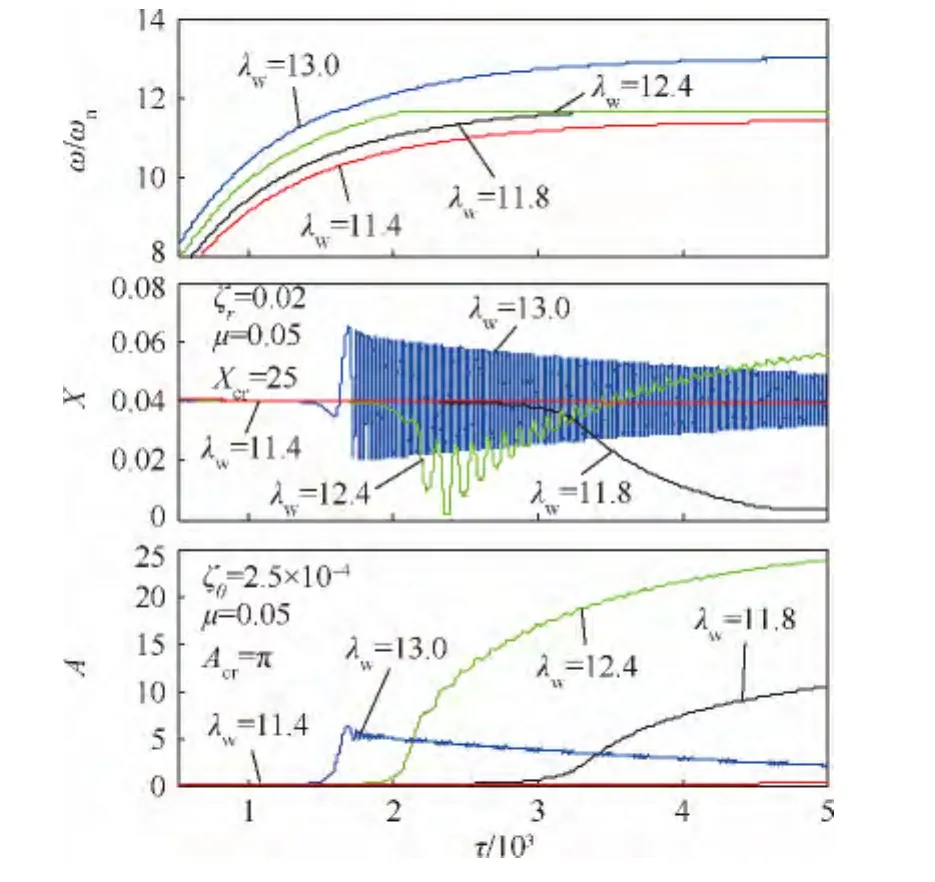
圖22 對(duì)稱厚盤轉(zhuǎn)子定功率過(guò)高階臨界轉(zhuǎn)速時(shí)隨時(shí)間變化的瞬態(tài)振動(dòng)曲線Fig.22 Transient vibration curves over time of symmetric thick-disk rotor crossing higher order critical speed with constant power

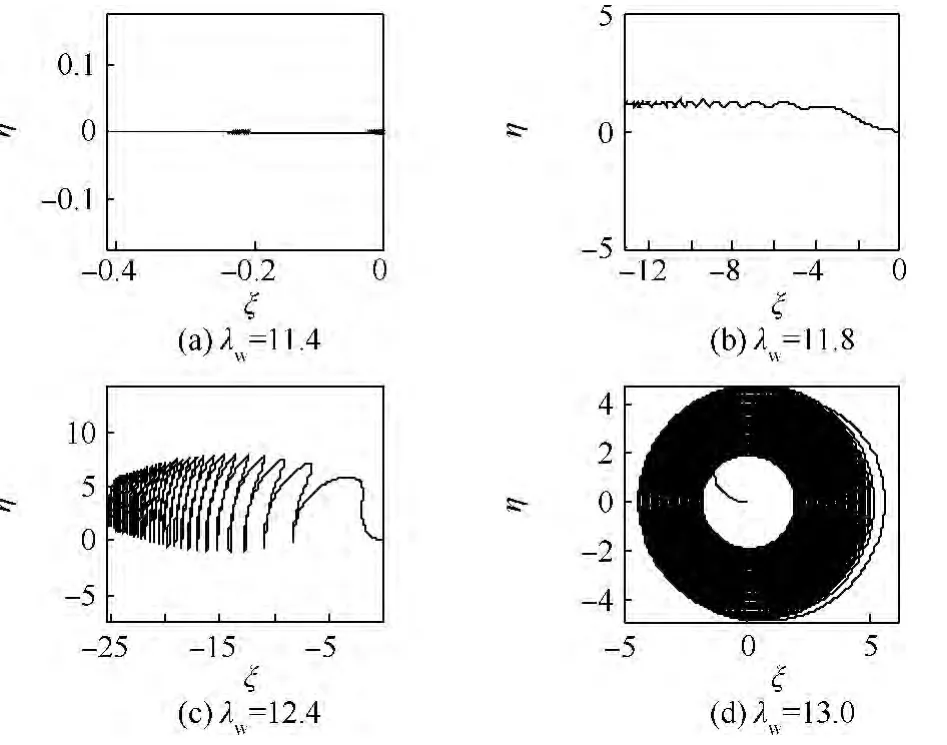
圖23 對(duì)稱厚盤轉(zhuǎn)子定功率過(guò)高階臨界轉(zhuǎn)速時(shí)盤偏角矢尖軌跡Fig.23 Trajectories of declination angle vector tip of disk of symmetric thick-disk rotor crossing higher order critical speed with constant power

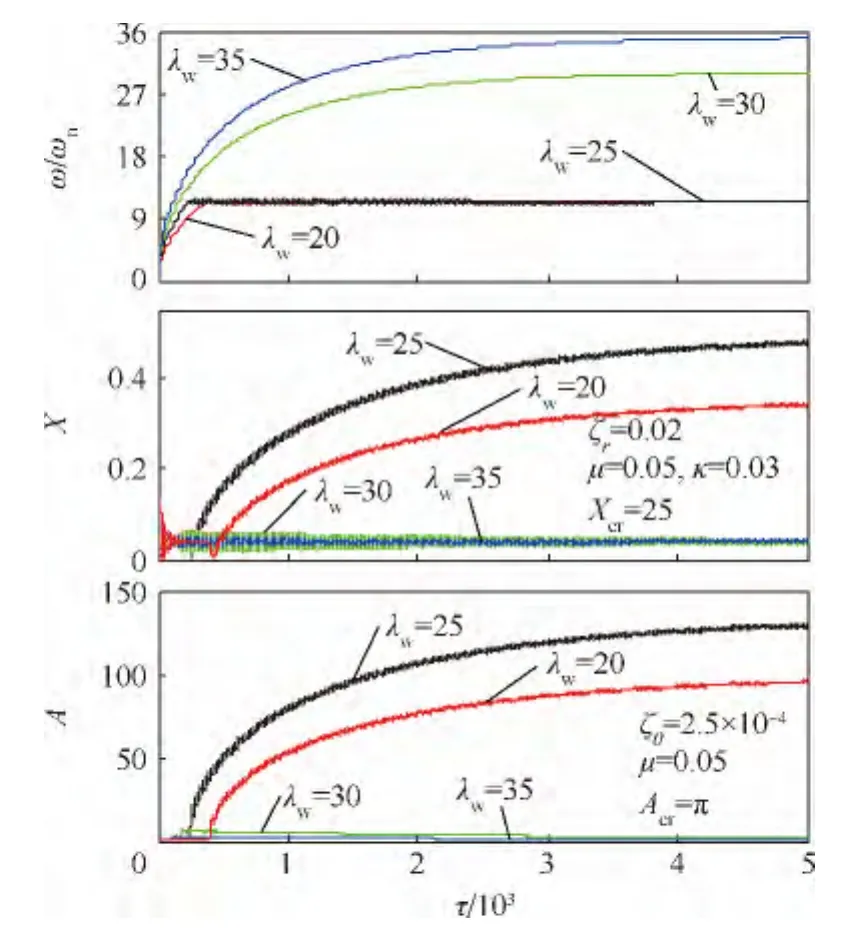
圖24 非對(duì)稱(κ=0.03)厚盤轉(zhuǎn)子定功率過(guò)高階臨界轉(zhuǎn)速時(shí)隨時(shí)間變化的瞬態(tài)振動(dòng)曲線Fig.24 Transient vibration curves over time of asymmetric thick-disk rotor(κ =0.03)crossing higher order critical speed with constant power

過(guò)臨界轉(zhuǎn)速需要的瞬態(tài)能量高于相同當(dāng)?shù)剞D(zhuǎn)速條件下穩(wěn)態(tài)的系統(tǒng)能量.而且，非對(duì)稱轉(zhuǎn)子比對(duì)稱轉(zhuǎn)子更不穩(wěn)定，更易發(fā)生非線性分叉，穿過(guò)臨界轉(zhuǎn)速需要的能量也更大.對(duì)需要穿過(guò)高階臨界轉(zhuǎn)速的對(duì)稱厚盤轉(zhuǎn)子系統(tǒng)，相較于低階臨界轉(zhuǎn)速，外界能源要提供更高的功率才能克服瞬態(tài)振動(dòng)引起的“失速”;而非對(duì)稱厚盤轉(zhuǎn)子由于能量有限幾乎不能穿過(guò)高階臨界轉(zhuǎn)速.

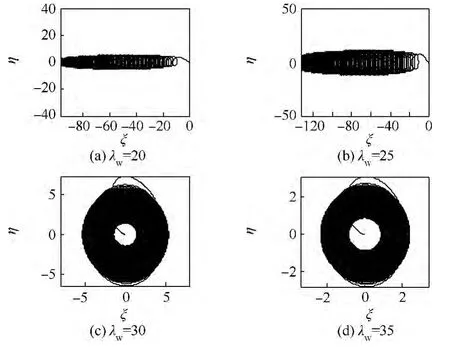
圖25 非對(duì)稱(κ=0.03)厚盤轉(zhuǎn)子定功率過(guò)高階臨界轉(zhuǎn)速時(shí)盤偏角矢尖軌跡Fig.25 Trajectories of declination angle vector tip of disk of asymmetric thick-disk rotor(κ =0.03)crossing higher order critical speed with constant power

根據(jù)本節(jié)采用有限能量對(duì)厚盤轉(zhuǎn)子瞬態(tài)振動(dòng)的計(jì)算，可以得到:

1)若外界能源的功率不足夠克服阻力和振動(dòng)，反而會(huì)與系統(tǒng)耦合，引起振動(dòng)急劇增大.轉(zhuǎn)速將處于亞臨界轉(zhuǎn)速上，不能達(dá)到原本在臨界轉(zhuǎn)速以上的工作轉(zhuǎn)速，發(fā)生“失速”.

2)若外扭矩功率不足夠克服振動(dòng)，系統(tǒng)將產(chǎn)生非線性瞬態(tài)振動(dòng)，軌跡會(huì)出現(xiàn)分叉，如圖15(c)和圖18(c)所示.

3)隨著轉(zhuǎn)子剛度不對(duì)稱性加強(qiáng)，系統(tǒng)的不穩(wěn)定區(qū)域逐漸擴(kuò)大.文獻(xiàn)［17］采用Floquet理論分析單盤轉(zhuǎn)子，也有同樣的結(jié)論.

4)如果外界能源有足夠大的功率，使轉(zhuǎn)子產(chǎn)生大自轉(zhuǎn)加速度，即能抑制系統(tǒng)過(guò)臨界轉(zhuǎn)速的大幅度振動(dòng)，可以順利穿過(guò)臨界轉(zhuǎn)速.且穿過(guò)臨界轉(zhuǎn)速后，系統(tǒng)仍能保持穩(wěn)定，瞬態(tài)振幅維持在很小的水平.這對(duì)于低階和高階臨界轉(zhuǎn)速都是成立的.這說(shuō)明，過(guò)臨界轉(zhuǎn)速的自轉(zhuǎn)角加速度對(duì)厚盤轉(zhuǎn)子的瞬態(tài)振動(dòng)的影響很大;發(fā)生非線性振動(dòng)不僅與系統(tǒng)本身的結(jié)構(gòu)有關(guān)，還與外界激勵(lì)有關(guān).

5 結(jié)論

本文計(jì)算并分析了單、厚盤轉(zhuǎn)子穿過(guò)低、高階臨界轉(zhuǎn)速時(shí)的瞬態(tài)振動(dòng)，并以轉(zhuǎn)子的形心和盤的偏擺角矢尖在旋轉(zhuǎn)坐標(biāo)系中的軌跡對(duì)有阻尼單、厚盤轉(zhuǎn)子的穩(wěn)定性進(jìn)行了分析，得出:

1)做正進(jìn)動(dòng)的單、厚盤轉(zhuǎn)子系統(tǒng)有兩階固有模態(tài)，其中低階振型為軸的彎曲，高階振型為盤的偏擺;高階模態(tài)是厚盤轉(zhuǎn)子的特有模態(tài).

2)厚盤轉(zhuǎn)子在穿過(guò)兩階臨界轉(zhuǎn)速時(shí)，發(fā)生由按系統(tǒng)固有頻率的自由振動(dòng)和在當(dāng)?shù)剞D(zhuǎn)速頻率下的強(qiáng)迫振動(dòng)合成的瞬態(tài)振動(dòng);其中過(guò)低階臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)服從普通單盤轉(zhuǎn)子的一般規(guī)律，過(guò)高階臨界轉(zhuǎn)速的瞬態(tài)振動(dòng)則與薄盤轉(zhuǎn)子系統(tǒng)的瞬態(tài)振動(dòng)有很大的不同.

3)單盤轉(zhuǎn)子的自轉(zhuǎn)角加速度對(duì)系統(tǒng)過(guò)臨界轉(zhuǎn)速時(shí)的瞬態(tài)影響十分顯著.加速度越大，共振時(shí)對(duì)振幅的抑制越強(qiáng)，但是過(guò)臨界轉(zhuǎn)速后的振蕩衰減越緩慢.

4)剛度非對(duì)稱對(duì)厚盤轉(zhuǎn)子系統(tǒng)的穩(wěn)定性影響十分顯著.非對(duì)稱系數(shù)κ越大，轉(zhuǎn)子越容易產(chǎn)生非線性振動(dòng)，不穩(wěn)定區(qū)域擴(kuò)大，甚至造成轉(zhuǎn)子失穩(wěn).

5)采用定功率的有限能量模式加速的厚盤轉(zhuǎn)子，當(dāng)外界能源不足夠提供轉(zhuǎn)子通過(guò)臨界轉(zhuǎn)速時(shí)，出現(xiàn)了能源與系統(tǒng)的能量耦合的“失速”，造成振動(dòng)急劇增大，產(chǎn)生了非線性瞬態(tài)振動(dòng)以及分叉.

References)

［1］袁惠群.轉(zhuǎn)子動(dòng)力學(xué)基礎(chǔ)［M］.北京:冶金工業(yè)出版社，2013:64.Yuan H Q.Basic theory of rotor-dynamics［M］.Beijing:Metallurgical Industry Press，2013:64(in Chinese).

［2］ Liu Z S，Huang S L，Su JX，et al.Nonlinear dynamic analysis of an unsymmetrical generator-bearing system［J］.Journal of Vibration and Acoustics，2007，129(4):448-457.

［3］劉占生，黃森林，蘇杰先，等.非對(duì)稱柔性轉(zhuǎn)子系統(tǒng)的動(dòng)力特性分析［J］.振動(dòng)工程學(xué)報(bào)，2002，15(2):210-214.Liu Z S，Huang S L，Su JX，et al.Dynamic analysis of unsymmetrical flexible rotor system［J］.Journal of Vibration Engineering，2002，15(2):210-214(in Chinese).

［4］ Shu X D，Chen L P，Wei X H.Analysis of axial deformation of cross wedge rolling asymmetric shaft part based on finite element method［J］.Applied Mechanics and Materials，2011，101-102:396-399.

［5］ Nandi A，Neogy S.An efficient scheme for stability analysis of finite element asymmetric rotor models in a rotating frame［J］.Finite Elements in Analysis and Design，2005，41(14):1343-1364.

［6］ Genta G.Whirling of unsymmetrical rotors:A finite element approach based on complex co-ordinates［J］.Journal of Sound and Vibration，1988，124(1):27-53.

［7］ Darpe A K，Gupta K，Chawla A.Transient response and breathing behaviour of a cracked Jeffcott rotor［J］.Journal of Sound and Vibration，2004，272:207-243.

［8］鄒劍，陳進(jìn)，董廣明.裂紋轉(zhuǎn)子過(guò)亞臨界轉(zhuǎn)速瞬態(tài)響應(yīng)特性［J］.上海交通大學(xué)學(xué)報(bào)，2003，37(7):1106-1109.Zou J，Chen J，Dong GM.Research on transient response characteristics of a cracked rotor passage through subcritical speed［J］.Journal of Shanghai Jiao Tong University，2003，37(7):1106-1109(in Chinese).

［9］ Sekhar A S.Transient analysis of a cracked rotor passing through critical speed［J］.Journal of Sound and Vibration，1994，173(3):415-421.

［10］張文.轉(zhuǎn)子動(dòng)力學(xué)理論基礎(chǔ)［M］.北京:科學(xué)出版社，1990:17.Zhang W.Basic theory of rotor-dynamics［M］.Beijing:Science Press，1990:17(in Chinese).

［11］方之楚，駱振黃.單盤轉(zhuǎn)子系統(tǒng)過(guò)臨界轉(zhuǎn)速時(shí)的瞬態(tài)響應(yīng)［J］.上海交通大學(xué)學(xué)報(bào)，1987，21(3):23-36.Fang Z C，Luo Z H.Transient response of single-disk rotor system on passing through critical speed［J］.Journal of Shanghai Jiao Tong University，1987，21(3):23-36(in Chinese).

［12］ Hassenpflug H L，F(xiàn)lack R D，Gunter E J.Influence of acceleration on the critical speed of a Jeffcott rotor［J］.Journal of Engineering for Power，1981，103(1):108-113.

［13］晏礪堂.結(jié)構(gòu)系統(tǒng)動(dòng)力特性分析［M］.北京:北京航空航天大學(xué)出版社，1989:183-186.Yan L T.Analysis on dynamic characteristics of structure system［M］.Beijing:Beihang University Press，1989:183-186(in Chinese).

［14］岳聰，任興民，鄧旺群.柔性轉(zhuǎn)子加速過(guò)臨界瞬態(tài)響應(yīng)特征分析［J］.機(jī)械科學(xué)與技術(shù)，2013，32(3):395-398.Yue C，Ren X M，Deng W Q.Analyzing transient response of flexible rotor across critical speeds［J］.Mechanical Science and Technology for Aerospace Engineering，2013，32(3):395-398(in Chinese).

［15］ Xiao X W，Yang S Z，Huang Y Y.1/2 subharmonic resonance of a shaft with unsymmetrical stiffness［J］.Chinese Journal of Mechanical Engineering，2003(1):26-30.

［16］林富生，孟光.重力對(duì)具有初彎和不對(duì)稱剛度機(jī)動(dòng)轉(zhuǎn)子特性的影響［J］.機(jī)械強(qiáng)度，2002，24(3):320-326.Lin F S，Meng G.Influence of gravity on the dynamics of a maneuvering rotor with initial bending and asymmetry［J］.Journal of Mechanical Strength，2002，24(3):320-326(in Chinese).

［17］陸鵬，葉黔元.電機(jī)轉(zhuǎn)子參數(shù)振動(dòng)的穩(wěn)定性分析［J］.上海海運(yùn)學(xué)院學(xué)報(bào)，2001，22(3):183-186.Lu P，Ye Q Y.The stability analysis of motor-rotor’s parameter vibration［J］.Journal of Shanghai Maritime University，2001，22(3):183-186(in Chinese).