基于碰撞航線的動(dòng)能攔截器滑模制導(dǎo)律設(shè)計(jì)

楊旭，張皎，劉源翔

(北京理工大學(xué) 宇航學(xué)院，北京 100081)

動(dòng)能攔截器(Kinetic Kill Vehicle，KKV)作為一種大氣層外高速飛行器，利用高速飛行產(chǎn)生的巨大動(dòng)能，通過(guò)直接碰撞摧毀來(lái)襲目標(biāo).與傳統(tǒng)大氣層內(nèi)制導(dǎo)武器相比，動(dòng)能攔截器采用直接力控制彈體姿態(tài)，以實(shí)現(xiàn)精準(zhǔn)攔截.因此制導(dǎo)律的設(shè)計(jì)是動(dòng)能武器實(shí)現(xiàn)精確攔截的關(guān)鍵［1］.

關(guān)于制導(dǎo)律國(guó)內(nèi)外開(kāi)展了大量的研究.其中應(yīng)用最為廣泛的是比例導(dǎo)引(proportional navigation)，其控制方式是令導(dǎo)彈加速度指令與彈目相對(duì)速度及視線角速率成比例［2］.但當(dāng)目標(biāo)做大機(jī)動(dòng)飛行時(shí)，比例導(dǎo)引難以保證準(zhǔn)確命中目標(biāo).文獻(xiàn)［3］提出了一種真比例制導(dǎo)率，通過(guò)控制導(dǎo)彈垂直于視線方向的加速度大小補(bǔ)償目標(biāo)機(jī)動(dòng)，達(dá)到了減小脫靶量的效果.谷志軍和陳磊［4］針對(duì)動(dòng)能攔截器順軌攔截問(wèn)題設(shè)計(jì)了一種比例導(dǎo)引律降低了導(dǎo)彈的需用過(guò)載，但該方法僅適用于導(dǎo)彈速度大于目標(biāo)速度的情況.

隨著控制理論的研究深入，許多學(xué)者提出了基于現(xiàn)代控制理論的制導(dǎo)律設(shè)計(jì)方法.如最優(yōu)制導(dǎo) 律［5-7］，滑 模 制 導(dǎo) 律［8-11］，backstepping 制 導(dǎo)律［12-13］，動(dòng)態(tài)面制導(dǎo)律［14-15］等.李浩和佘浩平［6］以彈目相對(duì)位置及相對(duì)速度為約束，設(shè)計(jì)了一種彈道成型的最優(yōu)制導(dǎo)律.Indig等［7］利用最優(yōu)控制理論，提出了一種改進(jìn)比例制導(dǎo)律.朱戰(zhàn)霞等［1］利用終端滑模理論設(shè)計(jì)了適用于動(dòng)能攔截器的末段制導(dǎo)律，通過(guò)在滑模面的設(shè)計(jì)中引入非線性函數(shù)，使得跟蹤誤差在有限時(shí)間快速收斂到零，但在初始階段該方法的需用過(guò)載偏大.張運(yùn)喜等［8］提出了一種基于有限時(shí)間收斂的滑模變結(jié)構(gòu)制導(dǎo)律，實(shí)現(xiàn)了制導(dǎo)系統(tǒng)的視線角速率快速收斂到零，由于該制導(dǎo)律針對(duì)的是地面固定目標(biāo)，故并未考慮目標(biāo)機(jī)動(dòng).Rao和 Ghose［10］針對(duì)目標(biāo)機(jī)動(dòng)設(shè)計(jì)了一種新型滑模變結(jié)構(gòu)制導(dǎo)律，該制導(dǎo)律將目標(biāo)的加速度及加速度的導(dǎo)數(shù)視為未知有界變量，并在控制量設(shè)計(jì)中對(duì)其補(bǔ)償.但該方法容易令導(dǎo)彈需求的法向過(guò)載過(guò)大，并產(chǎn)生高頻抖振現(xiàn)象.刁兆師和單家元［13］利用backstepping的思想，設(shè)計(jì)了一種考慮自動(dòng)駕駛儀動(dòng)態(tài)特性并含有攻擊角約束的制導(dǎo)律，但該方法會(huì)導(dǎo)致微分膨脹.為解決微分膨脹問(wèn)題Qu和Zhou［14］考慮導(dǎo)彈自動(dòng)駕駛儀二階動(dòng)態(tài)特性，設(shè)計(jì)了一種基于動(dòng)態(tài)面理論的制導(dǎo)律.

在實(shí)際應(yīng)用中，由于系統(tǒng)的某些狀態(tài)量及目標(biāo)某些參數(shù)難以測(cè)量，故對(duì)設(shè)計(jì)制導(dǎo)律所需要的未知量的估計(jì)顯得尤為重要.Zarchan［16］和Shima等［17］分別利用卡爾曼濾波(KF)及擴(kuò)展卡爾曼濾波(EKF)的方法對(duì)系統(tǒng)的狀態(tài)量及目標(biāo)的參數(shù)進(jìn)行估計(jì).Zhu等［18］利用擴(kuò)張狀態(tài)觀測(cè)器(ESO)對(duì)目標(biāo)的加速度實(shí)時(shí)估計(jì)，并利用滑模控制理論設(shè)計(jì)了一種變結(jié)構(gòu)制導(dǎo)律.Zhang等［19］利用積分滑模控制方法設(shè)計(jì)制導(dǎo)律，并將目標(biāo)的機(jī)動(dòng)視為有界干擾并通過(guò)非線性干擾觀測(cè)器對(duì)其實(shí)時(shí)估計(jì)，通過(guò)控制視線角速率有限時(shí)間趨近于零從而命中目標(biāo).

綜上所述，在攔截打擊目標(biāo)時(shí)，大多是針對(duì)導(dǎo)彈速度大小恒定，通過(guò)控制彈目視線角速率有限時(shí)間收斂至零為目標(biāo)設(shè)計(jì)的制導(dǎo)律.而這種方式使導(dǎo)彈以曲線彈道實(shí)現(xiàn)對(duì)目標(biāo)的攔截，同時(shí)對(duì)于動(dòng)能攔截武器也難以獲得最大的碰撞速度.

針對(duì)動(dòng)能攔截器軸向加速度不為零的情況，本文設(shè)計(jì)了一種基于碰撞航線(collision course)的滑模制導(dǎo)律.該制導(dǎo)律的核心思想，即利用姿態(tài)控制發(fā)動(dòng)機(jī)瞬間改變彈體姿態(tài)，產(chǎn)生用于改變速度方向的需用法向過(guò)載，使導(dǎo)彈的速度矢量始終指向預(yù)期的碰撞點(diǎn)，直至完成對(duì)目標(biāo)的攔截.在制導(dǎo)律設(shè)計(jì)過(guò)程中，將未知的目標(biāo)機(jī)動(dòng)視為有界干擾，利用非線性干擾觀測(cè)器(NDO)對(duì)其實(shí)時(shí)估計(jì)，并把估計(jì)值用于對(duì)目標(biāo)機(jī)動(dòng)的補(bǔ)償，實(shí)現(xiàn)對(duì)目標(biāo)的精確打擊.

1 彈目相對(duì)運(yùn)動(dòng)模型

目標(biāo)的攔截問(wèn)題，通過(guò)合理的解耦，可以將三維問(wèn)題轉(zhuǎn)化為兩個(gè)相互垂直平面內(nèi)的二維問(wèn)題，分別在兩平面內(nèi)獨(dú)立設(shè)計(jì)對(duì)應(yīng)的制導(dǎo)律.為研究方便，本文選擇在縱向平面場(chǎng)景內(nèi)研究.圖1描述了導(dǎo)彈與目標(biāo)在笛卡兒慣性坐標(biāo)系Oxy下的相對(duì)運(yùn)動(dòng)關(guān)系.分別定義導(dǎo)彈M和目標(biāo)T各參數(shù)變量的下標(biāo)為m和t.

為了簡(jiǎn)化問(wèn)題，假設(shè)導(dǎo)彈和目標(biāo)均為質(zhì)點(diǎn)，忽略導(dǎo)彈和目標(biāo)所受重力，且導(dǎo)彈的自動(dòng)駕駛儀及姿態(tài)控制系統(tǒng)均具有理想動(dòng)態(tài)特性.在極坐標(biāo)系下彈目的相對(duì)運(yùn)動(dòng)學(xué)方程為

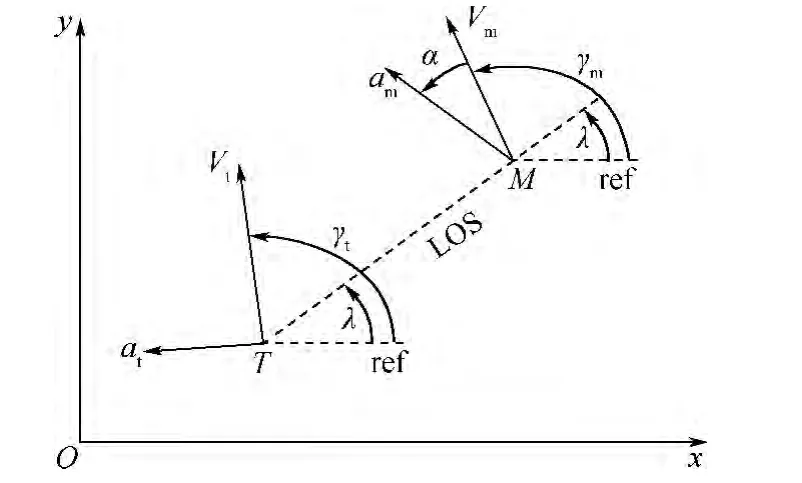
圖1 彈目攔截幾何Fig.1 Missile and target engagement geometry

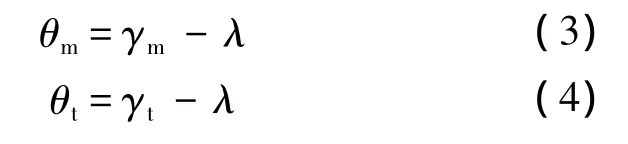
假設(shè)導(dǎo)彈可以通過(guò)火箭發(fā)動(dòng)機(jī)獲得沿彈軸方向恒定的加速度，忽略推力偏心.且能夠通過(guò)推力矢量發(fā)動(dòng)機(jī)實(shí)時(shí)改變彈體姿態(tài)即改變彈體的攻角α，從而使沿彈軸的加速度am可以指向需求的方向，則導(dǎo)彈速度的變化率和航跡角變化率滿足如下關(guān)系:

為方便研究，假定目標(biāo)運(yùn)動(dòng)速度Vt恒定且其加速度at的方向始終垂直于速度的方向，滿足如下關(guān)系:

2 基于碰撞航線的制導(dǎo)律設(shè)計(jì)

在本節(jié)中，設(shè)計(jì)一種基于碰撞航線的制導(dǎo)律，使攔截器能夠沿平直彈道運(yùn)動(dòng)至預(yù)期的碰撞點(diǎn).

當(dāng)導(dǎo)彈與目標(biāo)處于碰撞航線上時(shí)，同一時(shí)間內(nèi)導(dǎo)彈與目標(biāo)在垂直于視線方向的運(yùn)動(dòng)距離相同，則存在如下關(guān)系:

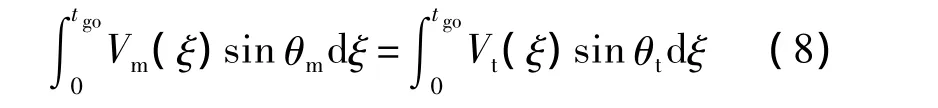
假設(shè)導(dǎo)彈加速度am的值恒定，且目標(biāo)做非機(jī)動(dòng)勻速運(yùn)動(dòng)，整理式(8)有

式中:tgo(time-to-go)為從當(dāng)前時(shí)刻至完成攔截所需要的時(shí)間.當(dāng)導(dǎo)彈與目標(biāo)處于并保持在碰撞三角形航線上運(yùn)動(dòng)時(shí)，存在如下關(guān)系［20］:

對(duì)tgo求導(dǎo)有

式中:θmr為導(dǎo)彈保持碰撞航線所需 θm的值;為導(dǎo)彈沿碰撞航線運(yùn)動(dòng)的平均速度，其導(dǎo)數(shù)為

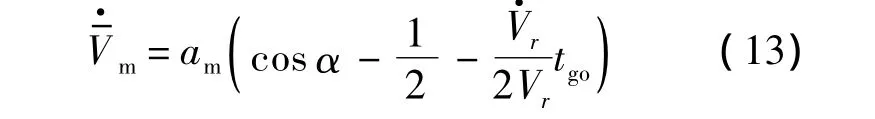
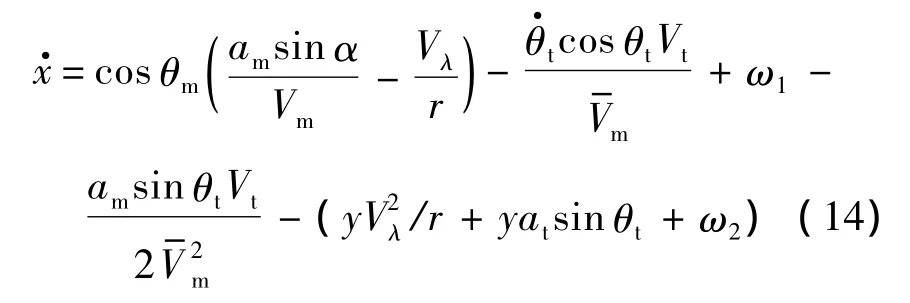
為實(shí)現(xiàn)跟蹤誤差的收斂，本文利用滑模控制理論來(lái)進(jìn)行制導(dǎo)律的設(shè)計(jì).選取滑模面S=x根據(jù)滑模運(yùn)動(dòng)可達(dá)性條件選擇如下趨近律:

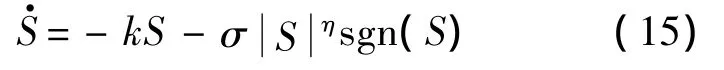
式中:k＞0，σ ＞0，0＜η ＜1.顯然式(15)所描述的趨近律能夠使系統(tǒng)的狀態(tài)量在有限時(shí)間內(nèi)從初值收斂到S的鄰域內(nèi).

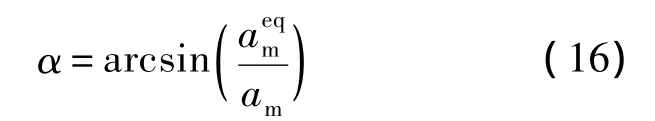
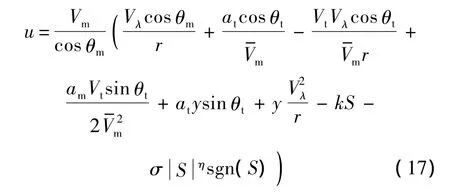
從式(17)可以看到，目標(biāo)的加速度出現(xiàn)在控制量中.由于實(shí)際導(dǎo)彈攔截中，目標(biāo)的加速度難以直接測(cè)量，因此采用NDO對(duì)目標(biāo)的加速度進(jìn)行估計(jì).

引理1［21］考慮如下單輸入單輸出(SISO)非線性系統(tǒng):

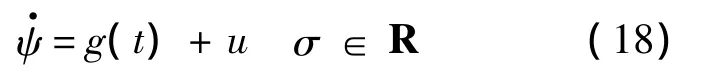
式中:ψ為系統(tǒng)的狀態(tài)量;u∈R為充分光滑的系統(tǒng)輸入;g(t)為充分光滑的不確定函數(shù).

定理1［22］考慮上述非線性系統(tǒng)(18)，假設(shè)u和ψ可測(cè)，g(t)有界且存在Lipschitz常數(shù)L＞0使得，則有如下觀測(cè)器:

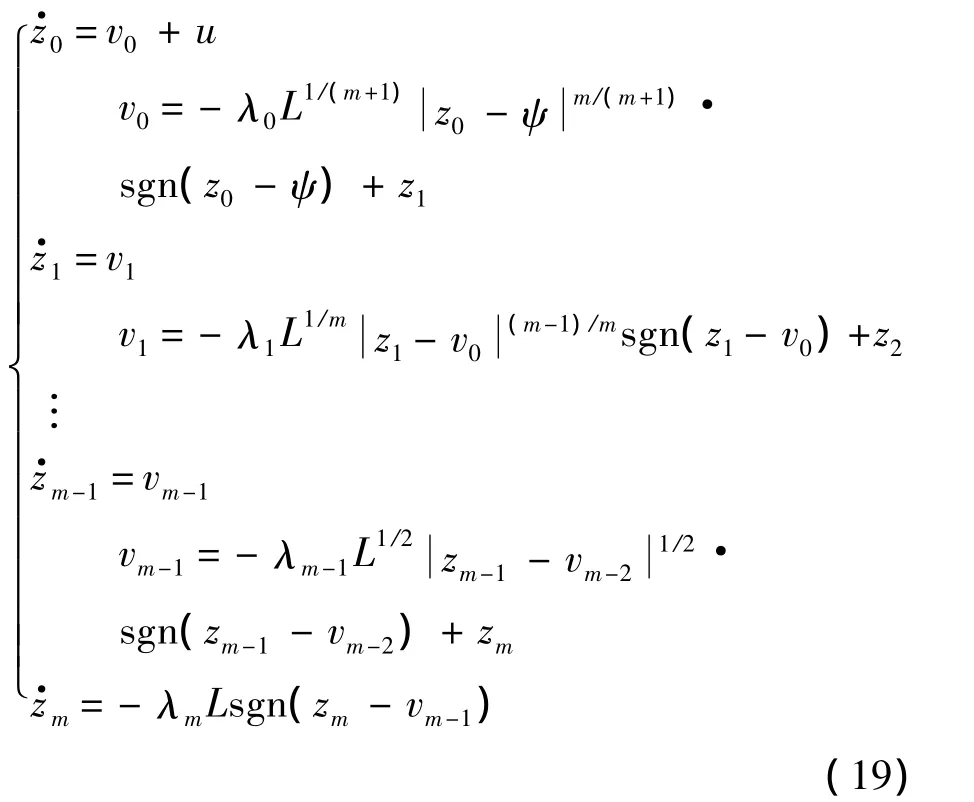
假設(shè)參數(shù)λi足夠大的，并忽略輸入噪聲，系統(tǒng)的狀態(tài)量及干擾的估計(jì)值將有限時(shí)間收斂，即

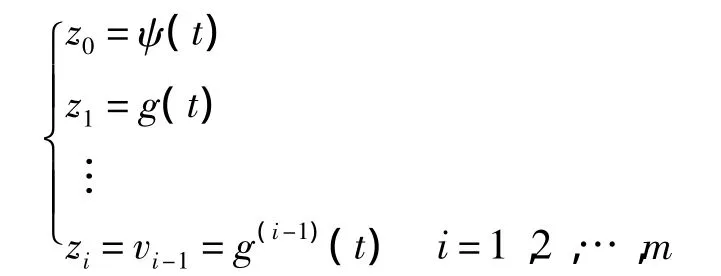
式(19)中參數(shù)λi的選取方法可參考文獻(xiàn)［23］，隨著λi的增大，觀測(cè)器的收斂速度加快，但觀測(cè)誤差將增大，同時(shí)對(duì)噪聲更加敏感，降低了觀測(cè)器的估計(jì)性能.因此，需要在仿真和實(shí)際應(yīng)用中合理地選取λi的值.

對(duì)式(2)求導(dǎo)得

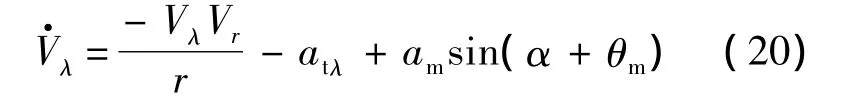
式中:atλ=atcosθt為目標(biāo)垂直于視線方向的加速度.設(shè)計(jì)觀測(cè)器如下:

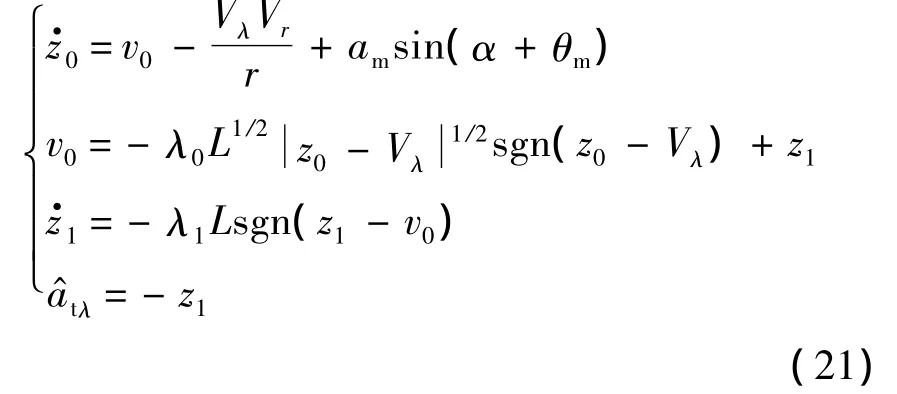
文獻(xiàn)［23］給出了NDO的穩(wěn)定性證明.假設(shè)Vλ，Vr，r，γm，λ 可測(cè)，且目標(biāo)法向加速度 at有界，則，其中分別為目標(biāo)加速度及其導(dǎo)數(shù)的上界［21］.由定理1可知觀測(cè)器參數(shù)，并通過(guò)合理地選擇 λ0，λ1，NDO的觀測(cè)誤差e=a^t－at將趨近于零，則z0和z1分別收斂于 Vλ和 －atλ.

目標(biāo)加速度at的估計(jì)值可表示為cosθt.聯(lián)立式(17)和式(21)，基于碰撞航線的導(dǎo)彈滑模制導(dǎo)律(NDOGC)虛擬控制量為

3 穩(wěn)定性分析

考慮如下非線性系統(tǒng)［24］:

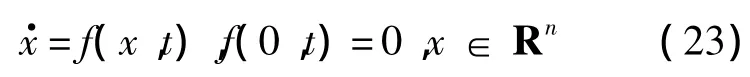
式中:f:U×R→Rn在U×R連續(xù);U為原點(diǎn)x=0的一個(gè)開(kāi)鄰域.

定理2 對(duì)于系統(tǒng)(23)，給定任意初始時(shí)刻t0的初始狀態(tài)x(t0)=x0∈U，存在一個(gè)依賴(lài)于x0的收斂時(shí)間T≥0，使系統(tǒng)方程以x0為初始狀態(tài)的解x(t)有定義，且有

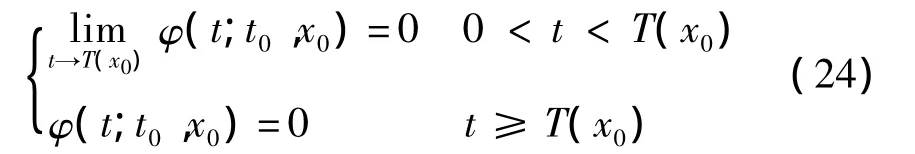
當(dāng) t∈［t0，T(x0))，φ(t;t0，x0)∈U{0}，那么系統(tǒng)的平衡點(diǎn)x=0是局部有限時(shí)間收斂的，如果U=Rn，則平衡點(diǎn)是全局有限時(shí)間收斂的.

引理2［24］考慮式(23)所描述的非線性系統(tǒng)，假設(shè)V(x)是定義在原點(diǎn)的鄰域U?R的C1光滑正定函數(shù).存在實(shí)數(shù)1＞β＞0及ρ＞0，使得)是定義域U?R的半負(fù)定函數(shù)，則存在定義域U0?U?R，使得定義在U0?R上的任意V(x)均能以有限時(shí)間收斂至原點(diǎn).若Tr為V(x)收斂至零的時(shí)間，則

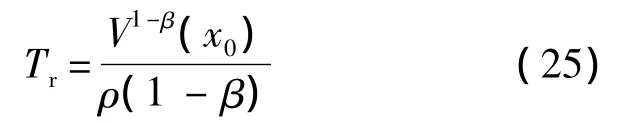
式中:x0為原點(diǎn)x=0某一開(kāi)鄰域中的任何一點(diǎn).如果U0=Rn且V(x)是徑向無(wú)界的(V(x)→+∞，當(dāng)，那么系統(tǒng)(23)的原點(diǎn)是全局有限時(shí)間收斂的.

定義如下的Lyapunov函數(shù):

由式(26)對(duì)時(shí)間t求導(dǎo)可得

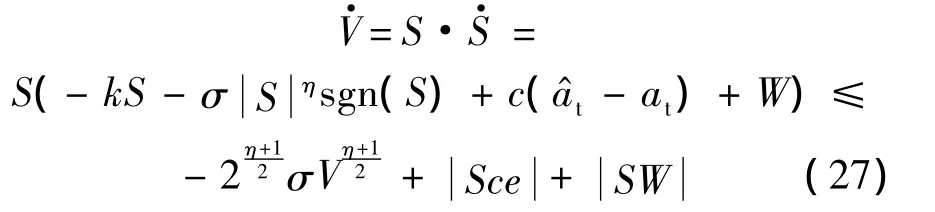
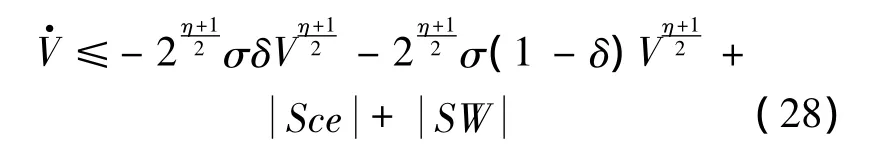
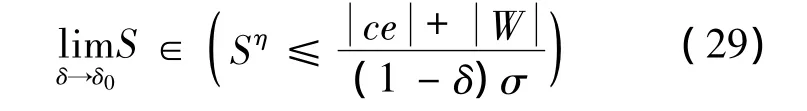
式中:0＜δ0＜1.函數(shù) V收斂至零的時(shí)間滿足式(30):

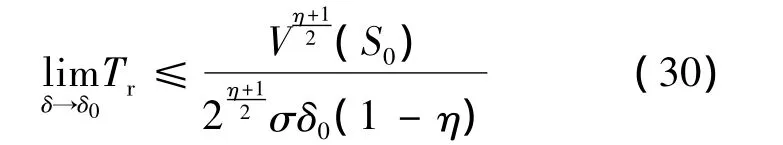
式中:S0為S的初值.

參數(shù)k，σ能夠保證當(dāng)滑模面S較大時(shí)，系統(tǒng)狀態(tài)量能以較大的速度趨近于滑動(dòng)模態(tài)，且隨k，σ增大系統(tǒng)有限時(shí)間收斂性越好，S的收斂速度越快.但過(guò)大的k，σ會(huì)導(dǎo)致系統(tǒng)的控制量過(guò)大，并產(chǎn)生抖振.通過(guò)調(diào)整參數(shù)η的值，可保證系統(tǒng)狀態(tài)量遠(yuǎn)離滑動(dòng)模態(tài)(S較大)時(shí)，能以較大的速度趨近于滑動(dòng)模態(tài)，當(dāng)系統(tǒng)狀態(tài)量趨近滑動(dòng)模態(tài)(S較小)時(shí)，保證較小的控制增益，以降低抖振.

4 仿真結(jié)果及分析

導(dǎo)彈在慣性坐標(biāo)系中的初始位置為xm(0)=50000m，ym(0)=0m，目標(biāo)的初始位置為xt(0)=yt(0)=0 m.導(dǎo)彈的初始航跡角 γm0∈［90°，160°］，目標(biāo)的初始航跡角 γt0∈［0°，90°］，導(dǎo)彈的加速度am=20 g.

由于式(22)中的符號(hào)函數(shù)sgn(S)會(huì)導(dǎo)致控制量的抖振，從而導(dǎo)致制導(dǎo)精度下降.選擇Sigmod函數(shù)代替，表達(dá)式為

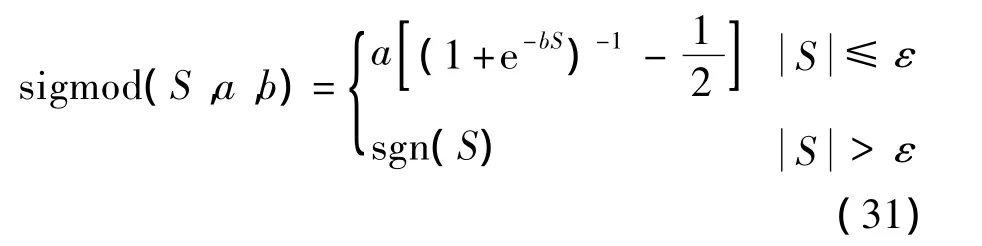
式中:ε為邊界層;參數(shù) a為幅值增益可調(diào)節(jié)sig(S，a，b)函數(shù)的幅值;參數(shù)b為指數(shù)因子可調(diào)節(jié)sig(S，a，b)函數(shù)的近似線性區(qū)間的范圍.本文選取的參數(shù)分別為 a=2，b=40，ε =0.2.

基于有限時(shí)間收斂理論設(shè)計(jì)的制導(dǎo)律(FTCG)是以零化視線角速率為目標(biāo)設(shè)計(jì)的，本文利用FTCG與NDOGC相對(duì)比，分析兩類(lèi)制導(dǎo)律的不同.FTCG采用如下形式［9］:

式中:N為大于2的常數(shù);μ＞0;0≤n＜1;f為目標(biāo)加速的上界.

兩種制導(dǎo)律相關(guān)參數(shù)分別為k=3，σ=5，η=0.5，L=80，λ0=1.5，λ1=1.1，N=10，μ =1.5，n=0.5，f=80.

4.1 攔截非機(jī)動(dòng)目標(biāo)

選取導(dǎo)彈和目標(biāo)的初始航向角分別為γm0=160°和γt0=20°，導(dǎo)彈和目標(biāo)的初始速度分別為Vm0=1 500m/s和 Vt0=3 000 m/s，仿真結(jié)果如圖2、圖3所示.

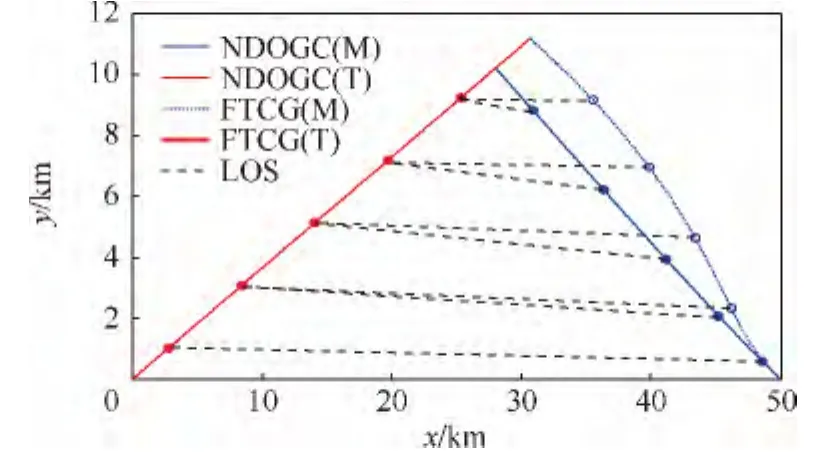
圖2 導(dǎo)彈和非機(jī)動(dòng)目標(biāo)相對(duì)運(yùn)動(dòng)軌跡Fig.2 Trajectories of missile and nonmaneuvering target relative motion

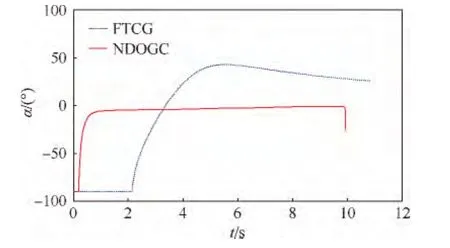
圖3 導(dǎo)彈和非機(jī)動(dòng)目標(biāo)的攻角變化Fig.3 Variation of angle of attack for missile and nonmaneuvering target

在NODGC制導(dǎo)律的作用下，導(dǎo)彈命中目標(biāo)需要9.94 s，脫靶量為0.18m，命中時(shí)刻導(dǎo)彈的速度為3431.3m/s，對(duì)于FTCG制導(dǎo)律，命中目標(biāo)需要10.87 s，脫靶量為 0.38m，命中時(shí)刻的速度為2942.8m/s.

從仿真結(jié)果可以看出，兩種制導(dǎo)律都可以有效地命中目標(biāo).從圖2可以看出，在NDOGC制導(dǎo)律的作用下，導(dǎo)彈的速度方向始終指向碰撞點(diǎn)，運(yùn)動(dòng)軌跡近似一條直線.在制導(dǎo)律FTCG的作用下，導(dǎo)彈通過(guò)改變航跡角使視線角速率趨近于零，這種方式迫使導(dǎo)彈以曲線運(yùn)動(dòng)軌跡命中目標(biāo).從圖3可以看出，導(dǎo)彈在NDOGC制導(dǎo)律的作用下，消除了初始航向誤差后，攻角近似為零，使導(dǎo)彈獲得更高的命中速度，這對(duì)提高動(dòng)能攔截器的殺傷效果是非常重要的.對(duì)比制導(dǎo)律FTCG，為保持視線角速率趨近于零需要不斷地調(diào)整導(dǎo)彈的攻角并最終收斂于常值，直至命中目標(biāo).這說(shuō)明導(dǎo)彈的加速度方向與速度方向不重合，難以充分利用導(dǎo)彈的加速度提高自身動(dòng)能.

4.2 攔截機(jī)動(dòng)目標(biāo)

選取導(dǎo)彈和目標(biāo)的初始航向角分別為γm0=160°和γt0=20°，導(dǎo)彈和目標(biāo)的初始速度分別為Vm0=1 500m/s和Vt0=3 000m/s，目標(biāo)以加速度at=8 g sin(0.5t)做正弦機(jī)動(dòng).仿真結(jié)果如圖4、圖5所示.

圖4 導(dǎo)彈和機(jī)動(dòng)目標(biāo)相對(duì)運(yùn)動(dòng)軌跡Fig.4 Trajectories of missile and maneuvering target relative motion

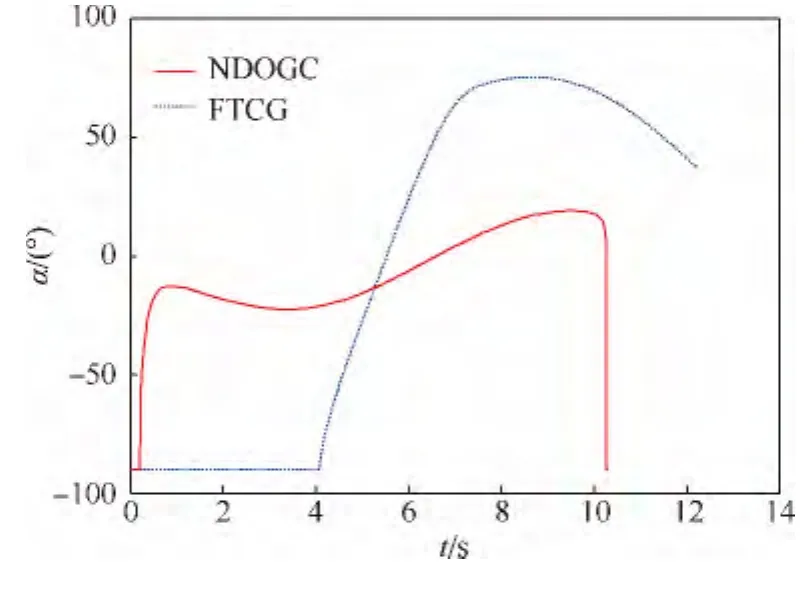
圖5 導(dǎo)彈和機(jī)動(dòng)目標(biāo)的攻角變化Fig.5 Variation of angle of attack for missile and maneuvering target

在NODGC制導(dǎo)律的作用下，導(dǎo)彈命中目標(biāo)需要10.28 s，脫靶量為 1.32m，命中時(shí)刻導(dǎo)彈的速度為3425.3m/s，對(duì)于FTCG制導(dǎo)律，命中目標(biāo)的時(shí)間為12.21 s，脫靶量為 4.06m，命中時(shí)刻的速度為 2369.2m/s.

從仿真結(jié)果可以看出，在目標(biāo)做大機(jī)動(dòng)運(yùn)動(dòng)時(shí)，制導(dǎo)律NDOGC的脫靶量更小，命中時(shí)間更短，命中速度更高.如圖4可知，相比于制導(dǎo)律FTCG，制導(dǎo)律NDOGC使導(dǎo)彈的運(yùn)動(dòng)軌跡更加平直，命中目標(biāo)耗時(shí)更短.其控制量變化如圖5，由于NDO對(duì)目標(biāo)加速度的實(shí)時(shí)估計(jì)，并在控制量中對(duì)目標(biāo)加速度變化帶來(lái)的擾動(dòng)進(jìn)行了有效的補(bǔ)償，降低了導(dǎo)彈需求的法向過(guò)載，故制導(dǎo)律NDOGC的攻角變化范圍更小，更有利于彈體的飛行穩(wěn)定.

考慮NDO對(duì)目標(biāo)加速度的觀測(cè)性能，如圖6所示.觀測(cè)器的估計(jì)值a^t可以穩(wěn)定地跟蹤目標(biāo)加速度的實(shí)際值at，說(shuō)明本文的干擾觀測(cè)器具有良好的性能，估計(jì)誤差較小.

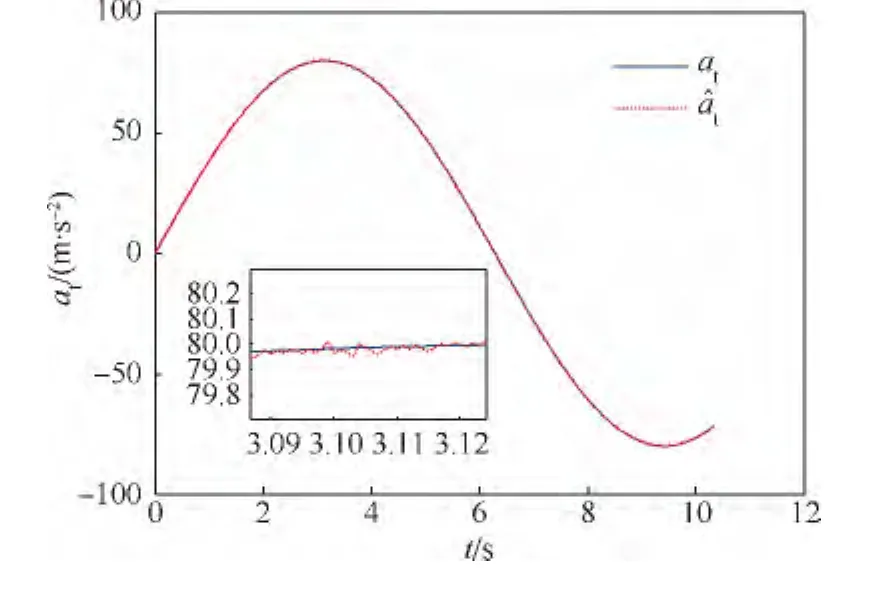
圖6 目標(biāo)加速度的估計(jì)Fig.6 Estimation of target acceleration

如圖7所示，設(shè)計(jì)的狀態(tài)反饋控制律能夠保證滑模面在有限時(shí)間趨近于零，實(shí)現(xiàn)基于碰撞航線的攔截策略.

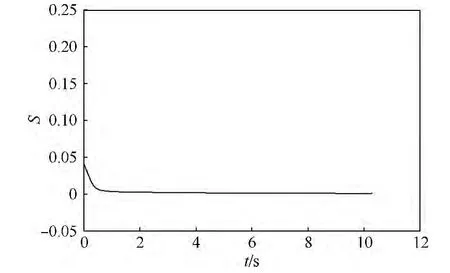
圖7 滑模面隨時(shí)間變化曲線Fig.7 Curve of sliding mode surface changing with time

4.3 可攔截區(qū)域分析

可攔截區(qū)域是評(píng)判制導(dǎo)律的主要指標(biāo)之一，是在有效攔截目標(biāo)并滿足一定約束條件下的導(dǎo)彈與目標(biāo)初始航跡角的集合.

本文定義當(dāng)脫靶量小于5m即認(rèn)為能夠有效攔截目標(biāo).選取導(dǎo)彈和目標(biāo)的初始航向角集合分別為 γm0∈［90°，160°］和 γt0∈［0°，90°］，導(dǎo)彈和目標(biāo)的初始速度分別為Vm0=1 500m/s和Vt0=3000m/s，目標(biāo)的最大過(guò)載為5g.

圖8 FTCG的攔截區(qū)域Fig.8 Capture zone of FTCG

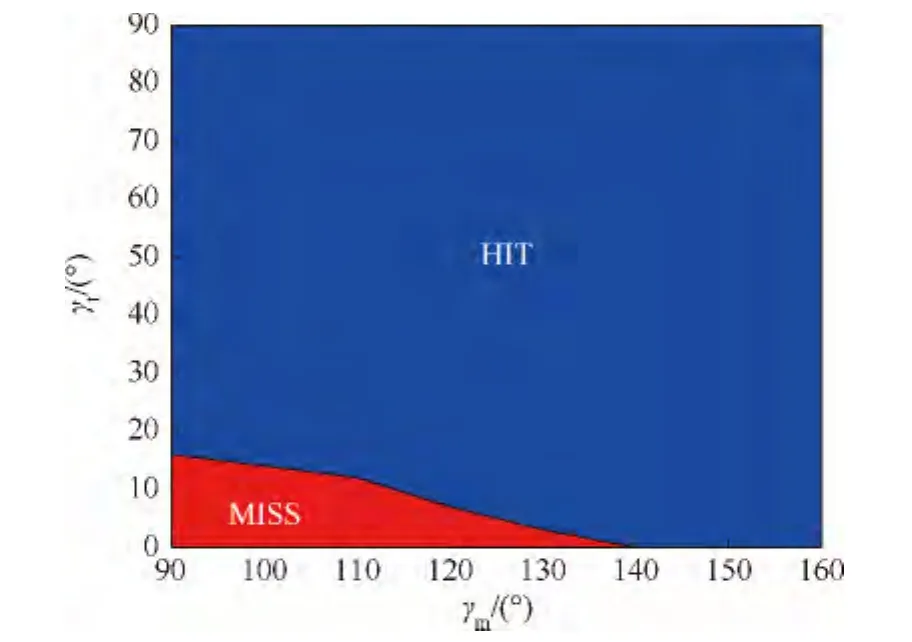
圖9 NDOGC的攔截區(qū)域Fig.9 Capture zone of NDOGC

仿真結(jié)果如圖8、圖9所示.圖中MISS表示導(dǎo)彈脫靶，HIT表示導(dǎo)彈命中目標(biāo).由結(jié)果可以看出，制導(dǎo)律NDOGC的可攔截區(qū)域遠(yuǎn)大于FTCG.NDOGC 僅在 γm0∈［90°，140°］，γt0∈［0°，17°］的小部分區(qū)域難以攔截目標(biāo)，在余下區(qū)域均可成功攔截.而 FTCG 在 γt0∈［0°，17°］及 γt0∈［34°，90°］的大部分區(qū)域都難以命中目標(biāo).故制導(dǎo)律NDOGC可適用的彈目初始航向角范圍更廣.

4.4 可攔截目標(biāo)速度范圍

對(duì)導(dǎo)彈而言，成功攔截目標(biāo)的速度區(qū)間也反應(yīng)了制導(dǎo)律的適用范圍.由于篇幅所限，本文僅以導(dǎo)彈和目標(biāo)的初始航向角分別為γm0=120°及γt0∈{20°，40°，60°}為例，分析兩種制導(dǎo)律的適用范圍.導(dǎo)彈的初始速度為Vm0=1 500m/s，目標(biāo)以加速度at=5g sin(0.5t)做正弦機(jī)動(dòng).

仿真結(jié)果如表1，在導(dǎo)彈初始航跡角、初始速度及加速度恒定的條件下，制導(dǎo)律NDOGC在目標(biāo)初始航跡角分別為 20°，40°，60°的條件下所攔截目標(biāo)的速度范圍均明顯大于制導(dǎo)律FTCG.仿真結(jié)果表明，對(duì)于高速機(jī)動(dòng)目標(biāo)攔截，NDOGC更加適用.

表1 兩種制導(dǎo)律攔截目標(biāo)的速度范圍Table 1 Velocity range of intercepting target for two guidance law

5 結(jié)論

針對(duì)動(dòng)能攔截器在大氣層外攔截機(jī)動(dòng)目標(biāo)且目標(biāo)加速度不可測(cè)等問(wèn)題，本文提出基于NDO和碰撞航線的新型滑模制導(dǎo)律.并與以零化視線角速率為目標(biāo)設(shè)計(jì)的有限時(shí)間收斂制導(dǎo)律對(duì)比，本文所述制導(dǎo)律能夠保證導(dǎo)彈以更短的時(shí)間、更小的過(guò)載、更大的末端速度實(shí)現(xiàn)對(duì)目標(biāo)的攔截.同時(shí)，擴(kuò)展了導(dǎo)彈的可攔截區(qū)域及可攔截目標(biāo)的速度范圍，具有較好的工程應(yīng)用前景.

References)

［1］朱戰(zhàn)霞，韓沛，陳鵬.基于非線性Terminal滑模的動(dòng)能攔截器末制導(dǎo)律設(shè)計(jì)［J］.西北工業(yè)大學(xué)學(xué)報(bào)，2013，31(2):233-238.Zhu Z X，Han P，Chen P.Design of nonlinear Terminal SMGL(sliding-mode guidance law)for KKV(kinetic kill vehicle)［J］.Journal of Northwestern Polytechnical University，2013，31(2):233-238(in Chinese).

［2］ Yuan L C.Homing and navigational courses of automatic target seeking devices［J］.Journal of Applied Physics，1948，19(12):1122.

［3］ Garnell P.Guided weapon control systems［M］.Oxford:Pergamon Press，1980:238-240.

［4］谷志軍，陳磊.大氣層外動(dòng)能攔截器順軌攔截技術(shù)研究［J］.宇航學(xué)報(bào)，2007，28(5):1195-1198.Gu Z J，Chen L.Research on interception along track for exoatmospheric［J］.Journal of Astronautics，2007，28(5):1195-1198(in Chinese).

［5］張友安，黃詰，孫陽(yáng)平.帶有落角約束的一般加權(quán)最優(yōu)制導(dǎo)律［J］.航空學(xué)報(bào)，2014，35(3):848-856.Zhang Y A，Huang J，Sun Y P.Generalized weighted optimal guidance laws with impact angle constraint［J］.Acta Aeronautica et Astronautica Sinica，2014，35(3):848-856(in Chinese).

［6］李浩，佘浩平.基于理想視線的彈道成型最優(yōu)導(dǎo)引律［J］.兵工學(xué)報(bào)，2014，35(8):1200-1204.Li H ，She H P.Trajectory shaping guidance law based on ideal line-of-sight［J］.Acta Armamentarii，2014，35(8):1200-1204(in Chinese).

［7］ Indig N，Ben-Asher J Z，F(xiàn)arber N.Near-optimal spatial midcourse guidance law with an angular constraint［J］.Journal of Guidance，Control，and Dynamics，2014，37(1):214-223.

［8］張運(yùn)喜，孫明瑋，陳增強(qiáng).滑模變結(jié)構(gòu)有限時(shí)間收斂制導(dǎo)律［J］.控制理論與應(yīng)用，2012，29(11):1413-1418.Zhang Y X，Sun M W，Chen Z Q.Sliding-mode variable structure finite-time convergence guidance law［J］.Control Theory ＆Applications，2012，29(11):1413-1418(in Chinese).

［9］ Zhou D，Sun S，Teo K L.Guidance laws with finite time convergence［J］.Journal of Guidance，Control，and Dynamics，2009，32(6):1838-1846.

［10］ Rao S，Ghose D.Terminal impact angle constrained guidance laws using variable structure systems theory［J］.IEEE Transactions on Control Systems Technology，2013，21(6):2350-2359.

［11］ Ran M P，Wang Q，Hou D L，et al.Backstepping design of missile guidance and control based on adaptive fuzzy sliding mode control［J］.Chinese Journal of Aeronautics，2014，27(3):634-642.

［12］舒燕軍，唐碩.軌控式復(fù)合控制導(dǎo)彈制導(dǎo)與控制一體化反步設(shè)計(jì)［J］.宇航學(xué)報(bào)，2013，34(1):79-85.Shu Y Y，Tang S.Integrated guidance and control backstepping design for blended control missile based on NDO［J］.Journal of Astronautics，2013，34(1):79-85(in Chinese).

［13］刁兆師，單家元.考慮自動(dòng)駕駛儀動(dòng)態(tài)特性的含攻擊角約束的反演遞推制導(dǎo)律［J］.宇航學(xué)報(bào)，2014，35(7):818-826.Diao Z S，Shan JY.Back-stepping guidance law with autopilot lag for attack angle constrained trajectories［J］.Journal of Astronautics，2014，35(7):818-826(in Chinese).

［14］ Qu P P，Zhou D.A dimension reduction observer-based guidance law accounting for dynamics of missile autopilot［J］.Proceedings of the Institution of Mechanical Engineers，Part G:Journal of Aerospace Engineering，2013，227(7):1114-1121.

［15］ Zhou D，Qu P P，Sun S.A guidance law with terminal impact angle constraint accounting for missile autopilot［J］.Journal of Dynamic Systems，Measurement，and Control，2013，135(5):51009.

［16］ Zarchan P.Representation of realistic evasive maneuvers by use of shaping filters［J］.Journal of Guidance，Control，and Dynamics，1979，10(4):434-439.

［17］ Shima T，Oshman Y，Shinar J.Efficient multiple model adaptive estimation in ballistic missile interception scenarios［J］.Journal of Guidance，Control，and Dynamics，2002，25(4):667-675.

［18］ Zhu Z，Xu D，Liu J，et al.Missile guidance law based on extended state observer［J］.IEEE Transactions on Industrial Electronics，2013，60(12):5882-5891.

［19］ Zhang Z，Li S，Luo S.Terminal guidance laws of missile based on ISMC and NDOB with impact angle constraint［J］.Aerospace Science and Technology，2013，31(1):30-41.

［20］ Ratnoo A，Ghose D.Collision-geometry-based pulsed guidance law for exoatmospheric interception［J］.Journal of Guidance，Control，and Dynamics，2009，32(2):669-675.

［21］ Bhat S P，Bernstein D S.Finite-time stability of continuous autonomous systems［J］.SIAM Journal on Control and Optimization，2000，38(3):751-766.

［22］ Shtessel Y B，Shkolnikov IA，Levant A.Smooth second-order sliding modes:Missile guidance application［J］.Automatica，2007，43(8):1470-1476.

［23］ Levant A.Higher-order sliding modes，differentiation and output-feedback control［J］.International Journal of Control，2003，76(9-10):924-941.

［24］ Hong Y.Finite-time stabilization and stabilizability of a class of controllable systems［J］.Systems ＆ Control Letters，2002，46(4):231-236.