某露天銅礦全境界開采規劃優化
畢春杰 戴曉江 宋小美
(昆明理工大學國土資源工程學院,云南 昆明 650093)
某露天銅礦全境界開采規劃優化
畢春杰 戴曉江 宋小美
(昆明理工大學國土資源工程學院,云南 昆明 650093)
基于數字礦床模型中的塊體模型,在給定的境界內,利用錐體排除法產生一系列地質最優開采體,建立動態規劃模型,以凈現值最大為目標函數,應用動態規劃法對最優開采體進行動態排序,就可以找到最優開采路徑作為最優開采方案。將上述方法應用于某露天礦,得出礦區的最佳開采年限為15 a,并給出了每年的開采區域、采礦量、剝巖量以及年末的累積凈現值。
開采計劃優化 錐體排除法 動態規劃 露天礦
確定露天礦開采工程實際合理的時空關系,是礦床開采過程中極具戰略性的關鍵因素[1]。 目前,國內外學者已經在露天礦開采規劃的優化方面做了很多的研究。比如黃光球[2]提出了露天礦分區開采的動態規劃模型,優化多分區開采采剝關系;張幼蒂[3]研究了采剝計劃和施工管理的整個系統的方案優化;Albach[4]在1967年應用線性規劃的方法求解出一個露天煤礦礦區的最佳產量,使礦山企業在滿足各種約束條件下獲得最大的總凈現值。Wang和Sevim[5]提出了露天開采整體優化的思想,并就金屬礦露天開采建立了整體優化模型和算法,本研究借鑒該方法的基本思想,對于一個圈定的露天坑境界,首先是利用錐體排除法產生一系列嵌套的地質最優開采體,以這些地質最優開采體作為工作幫坡角推進的候選位置,然后應用動態規劃法對這些地質最優開采體進行經濟評價,確定每年工作幫坡角的推進位置。
1 錐體排除法產生地質最優開采體原理
對于一個圈定的露天坑境界,如果一個采剝量為T、滿足工作幫坡角α約束的區段,所含有的金屬量是所有采剝量相同且滿足工作幫坡角α約束的區段中的最大者,則該區段稱為對應于T和α的地質最優開采體,如圖1,P1、P2、P3、P4即為地質最優開采體。
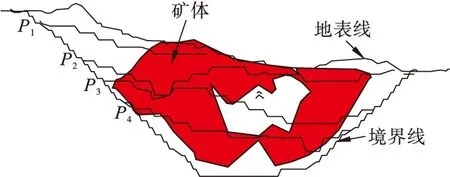
圖1 最終境界及其內的地質最優開采體序列
產生地質最優開采體的原理:以塊體模型為基礎,從最大的開采體PN(給定的境界)開始,在滿足開采體的邊坡角不大于最大工作邊坡角的條件下,從境界包含的塊體中剔除等于設定的開采體增量且金屬量最低的塊體的集合,得到倒數第2個開采體PN-1;如此重復,直到境界內剩余的礦巖量小于或者等于設定的最小年采剝總量,此時境界內剩余的礦巖量就形成了最小開采體P1。由于每次剔除的都是等于設定的采剝量中的金屬量最低的,即含礦物量最少的塊體集合,所以每次得到的開采體肯定是在相同條件下含金屬量最大的區域。
2 地質最優開采體動態規劃法排序
以產生的一系列最優開采體作為狀態,最優開采體數為階段數,一個階段的各種狀態就是這一系列最優開采體從小到大的排序。階段i上的狀態j只能由階段i-1的k狀態轉移而來,其中i-1≤k≤j-1。令mi,j(i-1,k)、qi,j(i-1,k)、ωi,j(i-1,k)分別為階段i-1上的狀態k轉移到階段i上的狀態j上的金屬量、礦量、巖量。假設礦石開采能力、采剝能力和選礦能力完全匹配,階段i-1上的狀態k轉移到階段i上的狀態j上需要的時間ti,j(i-1,k)為
階段i-1上的狀態k轉移到階段i上的狀態j上的利潤Pi,j(i-1,k)為
式中,A為年礦石生產能力;rm為礦石回采率;rp為選礦金屬回收率;gp為精礦品位;pi為階段i的精礦售價;y為廢石混入率;cm為采礦單位成本;cp為選礦單位成本;cw為剝巖單位成本。
平均利潤ai,j(i-1,k) 和小數部分利潤ri,j(i-1,k)為
式中,Li,j為ti,j(i-1,k)的整數部分。到達階段i的狀態j的累積時間Ti,j(i-1,k)為
階段i-1上的狀態k(i-1≤k≤j-1)轉移到階段i的狀態j上的累積凈現值NPVi,j(i-1,k)為
式中,d為折現率。
于是,動態規劃的遞歸目標函數為
將采剝計劃的每個階段的每個狀態的累積凈現值計算出來后,找到最大狀態的累積凈現值最大者,然后從該階段的該狀態反向搜索,便得到了最優的路徑方案,此路徑方案就是每個階段末幫坡角推進到的位置,組成了采剝計劃優化問題的最優解。
3 應用實例
為了驗證錐體排除算法模型和動態規劃模型在采剝計劃優化中的實用性,以某露天銅礦為工程背景,運用計算機進行編程,根據礦區收集到的資料進行礦區采剝計劃優化。此礦區已于2007年投產,本次全境界采剝計劃是在2012年末的采場現狀上,并滿足一定約束條件的情況下,對未開采部分的境界內礦巖的開采以凈現值最大化為目標,獲得在真正意義上最佳解的采剝計劃。
為了保證精度,同時考慮到程序的運行速度和礦山的實際情況,該礦區塊體以礦區臺階高度為塊體的高度,尺寸定為40 m×40 m×15 m,在X、Y、Z三維方向上共產生大量的塊體參與運算,如圖2所示。通過采剝計劃優化程序,提取的數據如表1所示。
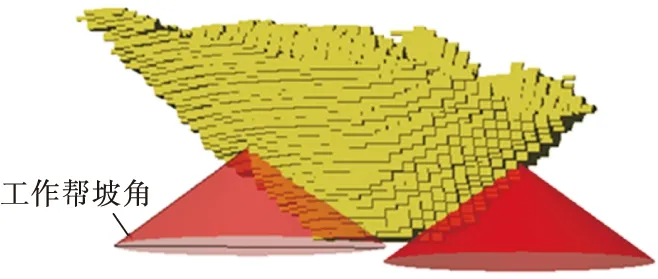
圖2 三維境界內產生地質最優開采體的示意
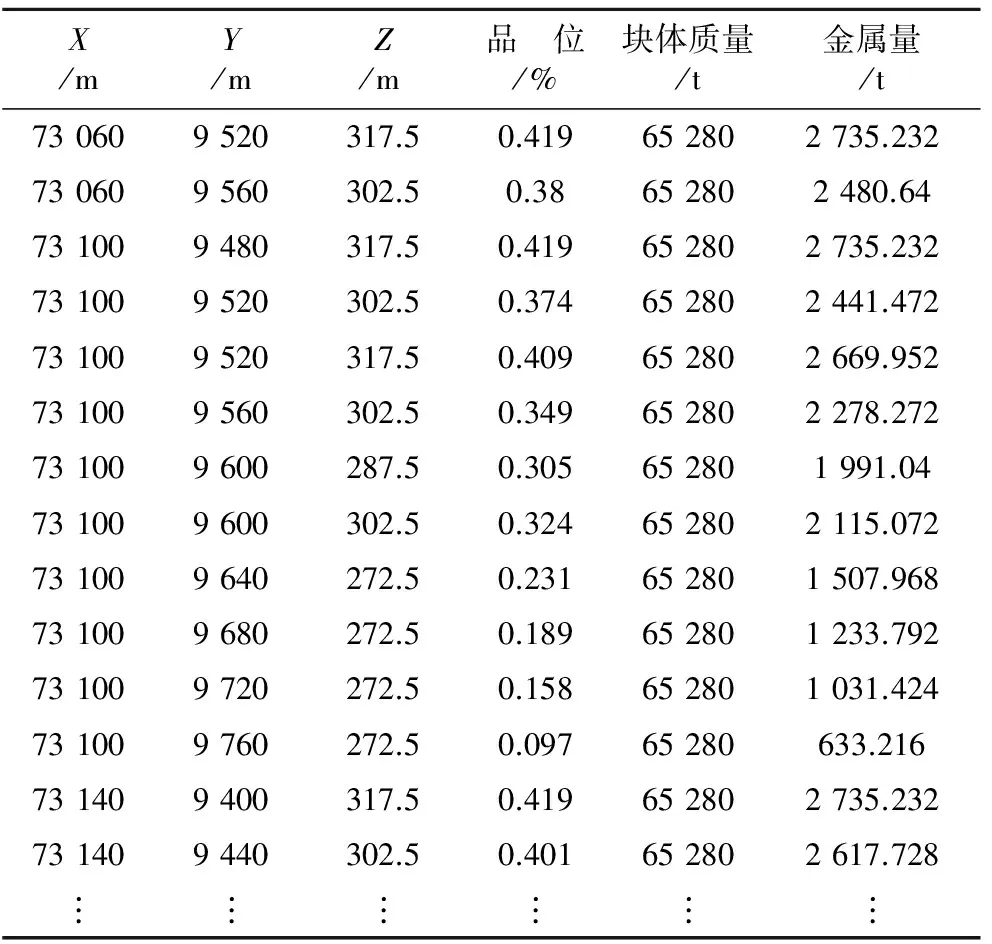
X/mY/mZ/m品 位/%塊體質量/t金屬量/t730609520317.50.419652802735.232730609560302.50.38652802480.64731009480317.50.419652802735.232731009520302.50.374652802441.472731009520317.50.409652802669.952731009560302.50.349652802278.272731009600287.50.305652801991.04731009600302.50.324652802115.072731009640272.50.231652801507.968731009680272.50.189652801233.792731009720272.50.158652801031.424731009760272.50.09765280633.216731409400317.50.419652802735.232731409440302.50.401652802617.728??????
本礦區所選用的礦區技術經濟指標如表2所示。

表2 某露天銅礦礦區技術經濟指標
由于本優化實例的礦區已經進行了境界優化,給定了最終境界,所以只需要以工作邊坡角為約束條件生成地質最優開采體序列。本礦區選取的最小年采剝量為1 000萬t,開采體增量為100萬t,礦區內礦巖總量為18 036.9萬t,將產生180個最優開采體,組成一個地質最優開采體序列。產生的地質最優開采體的狀態量如表3所示。
表3 某露天銅礦部分地質最優開采體的狀態量表
Table 3 The state of some optimum geologicalpits in a copper open-pit mine
t
將這一地質最優開采體序列置于動態規劃網絡圖中,以動態規劃模型對其進行動態排序。本實例采用全境界開采,以年為階段,地質最優開采體為狀態。由于企業給礦區下達的指標往往是年采礦量或者年采金屬量,因此,本實例以最小年采礦量、最大年采礦量、最小年采金屬量、最大年采金屬量為約束條件動態排序最優開采體,即確定每年末的工作邊坡角的推進位置。本實例的最優采剝計劃優化方案如表4所示,包括每年開采礦量、巖量、礦山服務年限。
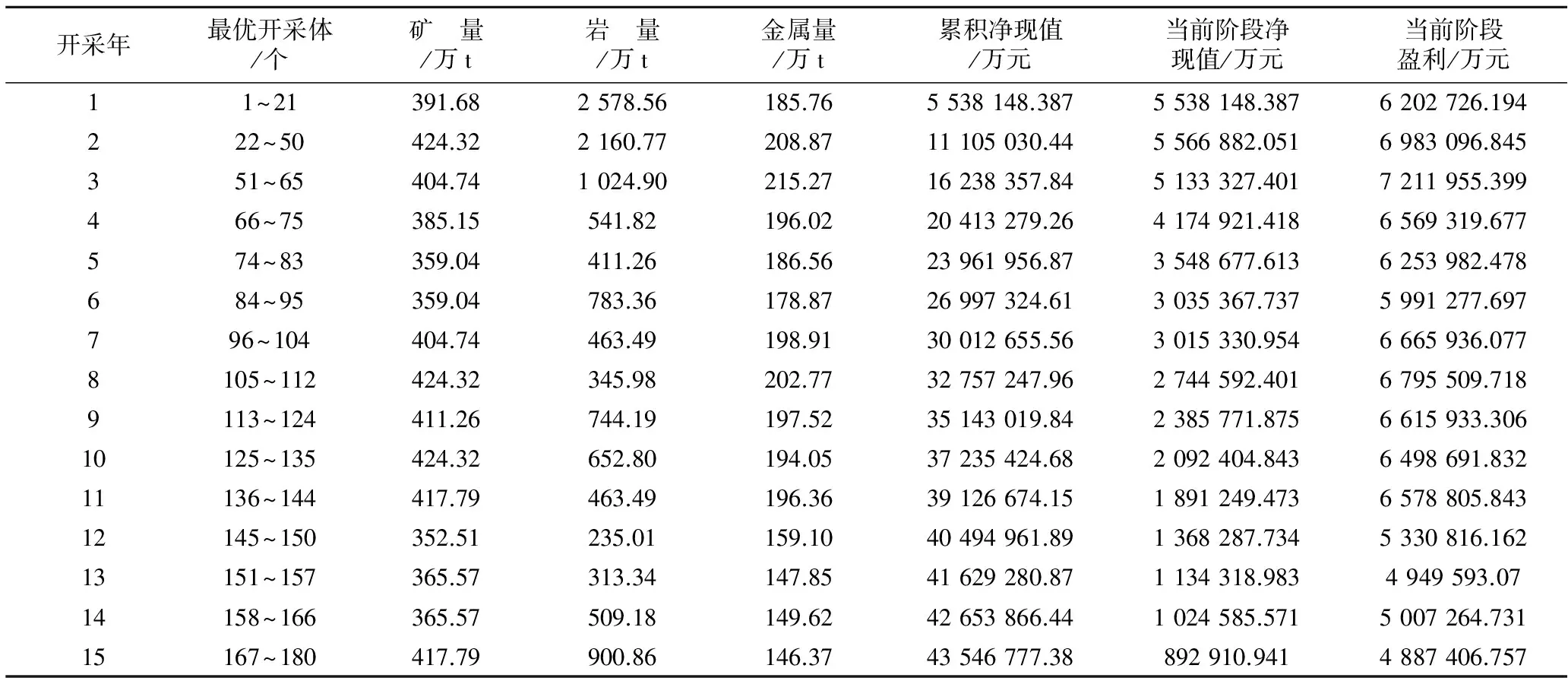
表4 某露天銅礦采剝計劃優化方案
由于本優化實例是以年為階段,所以此時的凈現值(NPV)計算會有所不同。凈現值的計算式變為
加入了采礦量和金屬量的約束條件, 根據修正后算法編制程序,然后進行動態排序,優化采剝計劃。
優化完成以后,將塊體的標記號作為塊體的一個新的屬性賦值到三維礦業軟件的塊體模型中,并根據優化結果進行塊體的顯示,不同顏色代表不同年的開采區域,如圖3所示。沿X方向、Y方向切剖開采區域,得到開采境界內的橫向剖面圖和縱向剖面圖,如圖4、圖5所示。
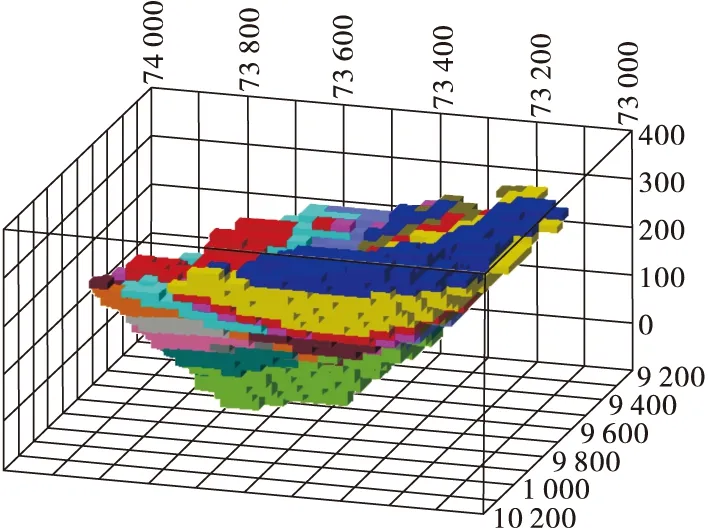
圖3 采剝計劃優化方案開采區域(單位:m)
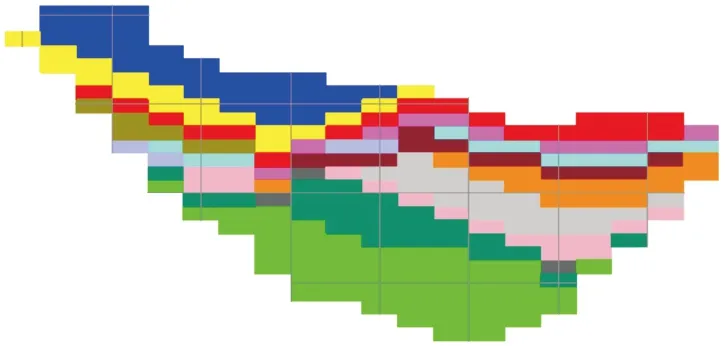
圖4 開采境界內橫向剖面
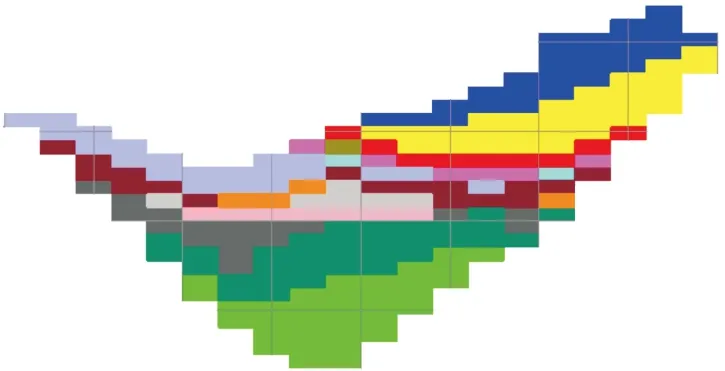
圖5 開采境界內縱向剖面
將帶有標記號屬性的塊體通過三維礦業軟件的采剝計劃編制的功能生成排查模型,可以得到每年末的礦區的采場現狀圖,如圖6所示。
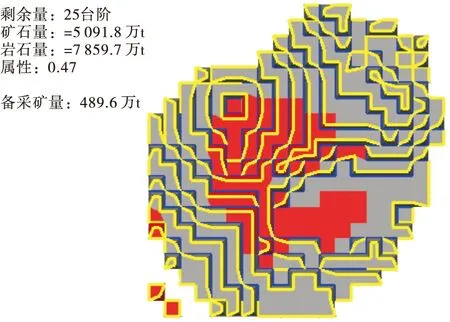
圖6 某露天銅礦第2年末采場現狀
由圖6可看出每年開采區域,開采后剩余的臺階數、礦量、巖量、備采礦量等信息,便于礦山企業的管理。
在動態排序的模型中加入階段開采礦量和金屬量的約束時,可以先使其波動范圍較小,根據優化結果可以很容易地看出設置的范圍過高或者過低。采剝計劃優化方案結果表明:①礦區的最佳開采年限為15 a;②每年的采礦量、剝離量和金屬量如表4所示,年采礦量和金屬量基本穩定,年采剝量有較大的波動;③開采順序為1,21,50,65,75,83,95,104,112,124,135,144,150,157,166,180,即第1年從第1個工作幫坡角的候選位置推進到第21個工作幫坡角候選位置,第2年從第22個工作幫坡角候選位置推進到第50個工作幫坡角候選位置,如此直到開采完整個開采境界。
4 結 語
介紹了應用錐體排除法產生地質最優開采體的原理和應用動態規劃法對地質最優開采體進行排序的算法,并且以某一露天銅礦余下的未開采區域為實例進行了優化,得到了每年的開采區域(采礦量、剝巖量)及每年末的累積凈現值,驗證了錐體排除算法模型和動態規劃模型在采剝計劃優化中的實用性。
[1] 牛成俊.現代露天開采理論與實踐[M].北京:科學出版社,1990:174-178. Niu Chengjun.The Modern Open-pit Mining Theory and Practice[M].Beijing:Science Press,1990:174-178.
[2] 黃光球.露天礦多分區開采采剝關系動態優化方法[J].冶金礦山設計與建設,1995(6):3-9. Huang Guangqiu.Dynamic optimization method open-pit stripping multi-partition mining relationship[J].Metal Mine Design & Construction,1995(6):3-9.
[3] 張幼蒂.露天礦剝采進度計劃優化研究現狀及發展趨勢[J].化工礦山技術,1996(6):2-9. Zhang Youdi.Research status and development trend of stipping and mining plan optimazation for open-pit[J].Chemical Mining Technology,1996(6):2-9.
[4] Albach H.Long range planning in open-pit mining[J].Management Science,1967,13(10):549-568
[5] Wang Q,Sevim H.Alternative to parameterization in finding a series of maximum metal pits for production planning[J].Mining Engineer,1995,298(2):178-182.
(責任編輯 石海林)
Optimization of the Whole Mining Plan in a Copper Open Pit
Bi Chunjie Dai Xiaojiang Song Xiaomei
(FacultyofLandResourcesEngineering,KunmingUniversityofScienceandTechnology,Kunming650093,China)
Based on the block model among the digital deposit models,and within a given region,the cone solution method was used to produce a series of optimal geological pits,and establish the dynamic programming model.With the maximized net present value as target function,the dynamic programming method was adopted to make the dynamic sequencing on the optimal pit.The optimal mining path can be chosen as the optimal mining scheme.Application of this scheme into a certain open-pit mine shows that its best service life is 15 years,and the annual mining area,mining amount,stripping quantity of rock,and the cumulative net present value at the end of each year are given respectively.
Mining optimization,Cone solution method,Dynamic programming,Open-pit mine
2015-06-05
畢春杰(1989—),男,碩士研究生。
TD854
A
1001-1250(2015)-10-033-04

