關于亞純函數φ(z)f(z)M[f]的值分布

金 瑾, 李 里

(1.畢節學院 數學系, 貴州 畢節 551700; 2.貴州電力職業技術學院 管理工程系, 貴陽 550003)

?

關于亞純函數φ(z)f(z)M[f]的值分布

金 瑾1*, 李 里2

(1.畢節學院 數學系, 貴州 畢節 551700; 2.貴州電力職業技術學院 管理工程系, 貴陽 550003)

設k和n0,n1,…,nk為任意的非負數,函數f(z)是復平面上超越亞純函數,函數φ(z)為f(z)的小函數,且φ(z)≡ /0.超越函數M[f]=(f(z))n0(f′(z))n1…(f(k)(z))nk.該文討論了超越亞純函數φ(z)f(z)M[f]值分布,提出一個新的定理,并進行了較為詳細的證明.

超越亞純函數;Nevanlinna理論; 值分布

1 引言與主要結果

195 9年,Hayman證明了下面的著名定理.

定理A[1]設f(z)為超越亞純函數,n為正整數,如果n≥3,則fn(z)f′(z)取每一個非零有窮復數無窮多次.

Hayman在文獻[2]中還猜測:定理A的結論對n=1和n=2也成立.1979年,Mues在文獻[3]中解決了n=2的情形.1995年,Bergweiler和Eremenko[4],陳懷惠和方明亮[5]獨立地解決了n=1的情形,并得到如下定理.

定理B[4-5]設f(z)為超越亞純函數,則f(z)f′(z)取每一個非零有窮復數無窮多次.

Sons,Steinmetz,楊重俊,楊樂,王躍飛等做了大量的工作并得到了許多重要的結果[6-11].

199 9年,龐學誠和Zalcman得到如下結果.

定理C[9]設f(z)為超越整函數,k和n為正整數,f(z)的所有零點的重數至少為k,則fn(z)f(k)(z)取每一個非零有窮復數無窮多次.

200 4年,張占亮對函數f(k)(z)-afn(z)進行了研究,并得到了如下結論.

定理D[15]設f(z)為平面內的超越亞純函數,a為非零有窮復數,則當n≥k+3時,函數f(k)(z)-afn(z)有無窮多個零點.

200 6年,王建平和儀洪勛在文獻[16]中證明了定理E和定理F.

定理E[16]設f(z)為超越亞純函數,k正整數(k≥2),f(z)的所有零點的重數至少為n,則對每一個k(k≥2),f(z)f(k)(z)取每一個非零有窮復數無窮多次.其中,當2≤k≤4時n=k+1;當k=5時,n=5;當k≥6時,n=6.

定理F[16]設f(z)為超越亞純函數,f(z)的所有零點的重數至少為n,則f(z)f(n)(z)取每一個非零有窮復數無窮多次.至多除去3個可能的例外正整數n=2,3,4.

200 6年,鄒溫林和張慶德將上述結果改進得到下面結果.

200 7年,江秀海和高凌云得到如下結論.

定理H[18]設f(z)為平面內的超越亞純函數,a為任意非零復數,對任意的正整數m,i0,i1,…,in,λ=i0+i1+…+in,Δ=i1+2i2+…+nin,則當m≥λ+Δ+2時,

wm+awi0(w′)i1(w″)i2…(w(n))in

可取無窮多個零點.

200 8年,方明亮又研究了f(z)+a(f′(z))n的值分布,得到下面結論.

定理I[19]設f(z)為平面內的超越亞純函數,a為非零復數,對任意的正整數n≥2,函數f(z)+a(f′(z))n取每一個有窮復數無窮多次.

本文利用亞純函數的Nevanlinna值分布理論和技巧,進一步探討亞純函數的值分布,得到如下結論.

這個結論改進了文獻[18-19,33-34]中的相關結論.

2 引理及其證明

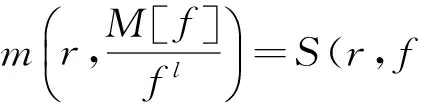
證明因

M[f]=(f(z))n0(f′(z))n1…(f(k)(z))nk,

且n0,n1,…,nk都是正整數.l=n0+n1+…+nk,所以

引理2設f(z)為復平面上的超越亞純函數,φ(z)為f(z)的不恒為零的小函數,φ(z)≡/0,M[f]=(f(z))n0(f′(z))n1…(f(k)(z))nk,k為正整數,n0,n1,…,nk為全為零的非負數.l=n0+n1+…+nk.則

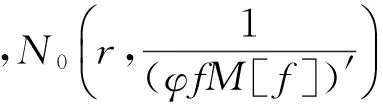
證明首先證明φ(z)fn(z)P[f]不恒為常數.

假設φ(z)f(z)M[f]為常數,則可設φ(z)f(z)M[f]=C(C為常數),顯然C≡/0,且

由此可得

故

這與f(z)為復平面上的超越亞純函數矛盾,即φ(z)fn(z)P[f]不恒為常數.

又由引理1及

可得

因此

(1)

記

(2)

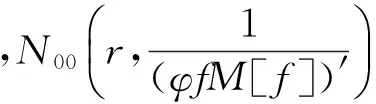
(3)

設z0為f(z)的p級零點,為φ(z)的t級極點,而且

則當p≤k,則z0為(φfM[f])′的至少為p+n0-t-1級零點;若t≥p,則z0至少為φ2(z)的極點.故

(4)

由(1)～(4)式可得

因此

成立.

引理3[32]設f(z)為復平面上的超越亞純函數,k為任意正整數,則

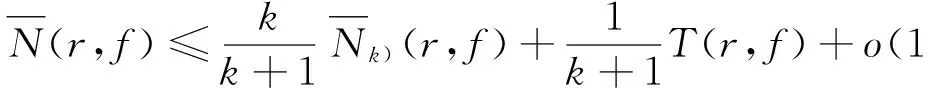
引理4[32]設f(z)為復平面上的超越亞純函數,則

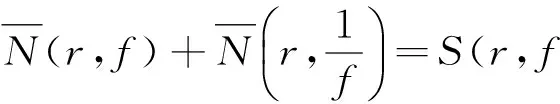
引理5設f(z)為復平面上的超越亞純函數,n和k為任意正整數,則

證明由引理2、引理3和引理4可得

所以

3 定理的證明

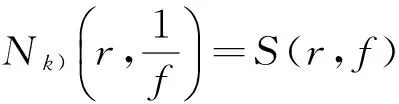
所以

即

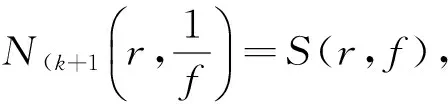
因此

由此得到φfM[f]取每一個非零有窮復數無窮多次.定理1證畢.

[1]HaymanWK.Picardvalueofmeromorphicfunctionandtheirderivatives[J].AnnMath, 1959, 70:9-42.

[2]HaymanWK.ResearchProblemsinFunctionThery[M].London:AthlonePrees, 1967.

[3]MuesE.UbereinproblemvonHayman[J].MathZ, 1979, 164:239-259.

[4]BergweilerW,EremenkoA.Onthesingularitiesoftheinversetoaofmeromorphicfunctionoffiniteorder[J].RevMatIberoamericana, 1995, 11:355-373.

[5]ChenHH,FangML.Onthevaluedistributionoffnf′[J].Science in China, 1995, A38:789-798.

[6] Sons L R.Deficiencies of monomiais[J].Math Z, 1969, 111:53-68.

[7] Steinmetz N. über die nullstellen von differential polynomen[J].Math Z, 1981, 176:255-264.

[8] Yang C C,Yang L,Wang Y F.On zeros of (f(k))n-a[J].China Sci Bull(in Chinese), 1993, 38:2215-2218.

[9] Pang X C,Zalcmam L.On theorems of Hayman and clunie[J].New Zealand J Math, 1999, 28:71-75.

[10] Wang J P.On the zeros offnf(k)-c(z)[J].Complex Variables, 2003, 48(8):695-703.

[11] Wang J P.On the zeros of the entire functionf(k)f-a[J].Chin Advances in Math(in Chinese), 2002, 31:41-46.

[12] Hayman W K.Meromorphic Functions[M].Oxford:Clarendon Press, 1964.

[13] Yi Hongxun,Yang Chungchun. Uniqueness Theory of Meromorphic Functions[M].Kluwer: Science Press, 2003.

[14] Doeringer W.Exceptional values of differetial polynomials[J].Pacific J of Math, 1982, 98:55-62.

[15] Zhang Zhanjing.On the zerosf(k)(z)-afn(z)[J].Mathematics in Practice and Theory(in Chinese), 2004, 31(11):129-134.

[16] Wang Jianping,Yi Hongxun. A fundamental inequality of the theory of meromorphic function and its applications[J].Acta Mathematica Sinica Chinese Series, 2006, 49(2):443-450.

[17] Zou Wenlin,Zhang Qingde.On distribution ofφ(z)fn(z)f(k)(z)[J].Journal of Sichuan Normal University:Natural Science, 2008, 31(6):662-666.

[18] Jiang Xiuhai,Gao Lingyun.The value distribution of functionwm+awi0(w′)i1…(w(n))in[J].Pure and Applied Mathematics(in Chinese), 2007, 23(1):17-20.

[19] Fang Mingliang, Zalcman L.The value distribution of functionf(z)+a(f′(z))n[J].Scien in China press(in Chinese), 2008, 38(3):279-285.

[20] Clunie J.On integral and meromorphic function[J].J London Math Soc, 1962, 98:55-62.

[21] He Yuzan,Xiao Xiuzhi.Algebroidal Function and Ordinary Differential Equations[M].(in Chinese)Beijing:Science Press, 1988.

[22] Golubew W W.Vorlesungen Uber Differentialgleichung in Komplexen[M].Berlin:Dduerscher Verlagder Wissenschten, 1958.

[23] Liu Huifang.On the growth of solutions of a class of differential equations with meromophic coefficients[J].Pure and Applied Mathematics, 2008, 24(1):25-29.

[24] Chen Yu.On the growth of meromophic solutions of a claas of linear differential equations[J].Pure and Applied Mathematics, 2009, 25(2):261-267.

[25] 金 瑾.關于高階線性微分方程解與其小函數的增長性[J].上海交通大學學報:自然科學版, 2013, 47(7):1155-1159.

[26] 金 瑾.一類高階齊次線性微分方程解的增長性[J].華中師范大學報:自然科學版, 2013, 47(1):4-7.

[27] 金 瑾.關于一類高階齊次線性微分方程解的增長性[J].中山大學學報:自然科學版, 2013, 52(1):51-55.

[28] 金 瑾.高階微分方程解與其小函數的關系[J].高校應用數學學報, 2013, 28(1):43-51.

[29] 金 瑾.一類高階齊次線性微分方程亞純解的超級及不動點[J].華中師范大學學報:自然科學版, 2011(1), 45(1):18-22.

[30] 金 瑾.單位圓內高階齊次線性微分方程解與不動點的研究[J].江西師范大學學報:自然科學版, 2013, 37(4):406-410.

[31] 金 瑾.單位圓內高階齊次線性微分方程解與不動點的研究[J].重慶師范大學學報:自然科學版, 2013, 37(4):406-410.

[32] 儀洪勛,楊重駿.亞純函數唯一性理論[M].北京:科學出版社, 1995: 173-238.

[33] 金 瑾.關于亞純函數φ(z)fn(z)f(k)(z)的值分布[J].純粹數學與應用數學, 2012(6):1-8.

[34] 李 偉,吳天毅.關于一般微分單項式的值分布[J].系統科學與數學, 2002, 22(10):58-66.

The value distribution of the meromorphic functionφ(z)f(z)M[f]

JIN Jin1, LI Li2

(1.Department of Mathematics, Bijie University, Bijie, Guizhou 551700;2.Department of Management Engineering， Guizhou Electric Power Vocational and Technical College， Guiyang 550003)

Let kandn0,n1,…,nkbe positive integers,f(z) be a transcendental meromorphic function in the complex plane,φ(z) be small function off(z), andφ(z) ≡ /0. The transcendental meromorphicM[f]=(f(z))n0(f′(z))n1…(f(k)(z))nk. In this paper, the value distributions of transcendental meromorphic functionφ(z)f(z)M[f] are discussed, and a new theorem and the detail proof are presented.

transcendental meromorphic function; Nevanlinna theory; value distribution

2014-11-16.

貴州省科學技術基金項目 (2012GZ10526);貴州省畢節地區科研基金項目(201102).

1000-1190(2015)04-0483-05

O174.5< class="emphasis_bold">文獻標識碼： A

A

*E-mail: jinjin62530@163.com.