判定連續隨機變量獨立性的兩個充要條件
王凡彬
(1.內江師范學院數學與信息科學學院,四川內江 641100;2.四川省高等學校數值仿真重點實驗室,四川內江 641100)
在多維隨機變量 (X1,X2,…,Xn) 中,各分量X1,X2,…,Xn獨立性的探討目前主要還是按定義進行的,即按如下兩個定義之一進行。
定義1 設n維隨機變量(X1,X2,…,Xn)的聯合分布函數為F(x1,x2,…,xn),Fi(xi)為Xi的邊際分布函數〔1〕。如果對任意n個實數x1,x2,…,xn,有
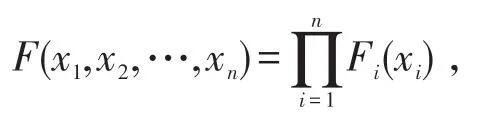
則稱X1,X2,…,Xn相互獨立。
定義2 設(X1,X2,…,Xn)為n維連續隨機變量,p(x1,x2,…,xn)為聯合密度函數,pi(xi)為Xi的密度函數〔1〕,如果對任意n個實數x1,x2,…,xn,有
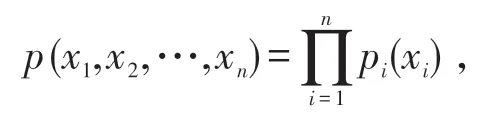
則稱X1,X2,…,Xn相互獨立。
按如上兩個定義對實際問題中的隨機變量的獨立性進行判定是較為困難和麻煩的。目前,對n維隨機變量(X1,X2,…,Xn)各分量獨立性的判定有一些研究〔2-10〕,但成果不多,或結果不夠好,不能用兩種方法進行處理。本文通過研究,得到了一個判定連續隨機變量獨立性的兩個充要條件,使得該問題的處理變得容易,提高了工作效率。
1 獨立性的判定
以下以二維連續隨機變量(X,Y)中X,Y的獨立性的判定討論為主,更高維情形的研究是類似的。
首先,從(X,Y)的聯合密度函數方面考慮,得到如下定理1。
定理1 設二維連續隨機變量(X,Y)的聯合密度函數為p(x,y),(x,y)∈D,D為 R2中的區域;其余,p(x,y)=0。則X,Y相互獨立的充要條件是:
(1)p(x,y)=φ(x)ψ(y),
(2)D=(a,b)×(c,d),
其中φ(x),ψ(y)分別為(a,b),(c,d)上的可積函數;a,b,c,d為實數,a,c可為-∞,b,d可為+∞。
證明:(充分性)按條件(1)、(2),X的邊際密度函數
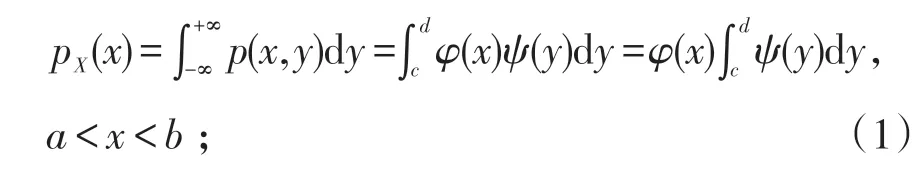
其余,pX(x)=0。
Y的邊際密度函數為
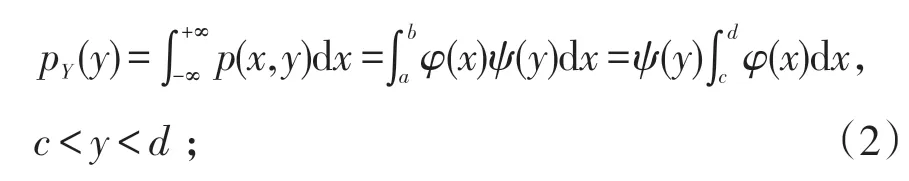
其余,pY(y)=0。則
其余,pX(x)pY(y)=0。(3)式的成立用到了
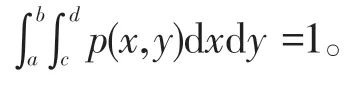
按獨立性定義,X,Y相互獨立。
(必要性)若X,Y相互獨立,則
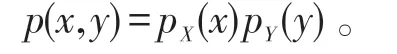
取pX(x)=φ(x),pY(y)=ψ(y),則條件(1)成立;又X,Y相互獨立,x,y的取值互相不影響,故D=(a,b)×(c,d),即條件(2)成立。
注1:定理1 條件(1)中,分解式p(x,y)=φ(x)ψ(y)不具有唯一性。
其次,從(X,Y)的聯合分布函數方面考慮,有下面的定理2。
定理2 設二維連續隨機變量(X,Y)的聯合分布函數為F(x,y),(x,y)∈D,D為 R2中的區域;其余,F(x,y)=0。則X,Y相互獨立的充要條件是:
(1)F(x,y)=f(x)g(y),
(2)D=(a,b)×(c,d),
其中f(x),g(y) 分別為(a,b),(c,d) 上的可導函數;a,b,c,d為實數,a,c可為-∞,b,d可為+∞。
證明:(充分性)當條件(1)、(2)成立時,(X,Y)的聯合密度函數為
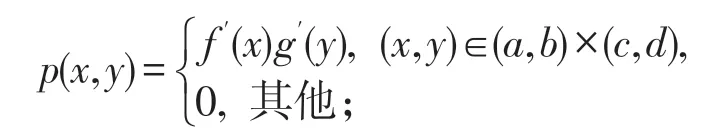
令φ(x)=f′(x),ψ(y)=g′(y),則
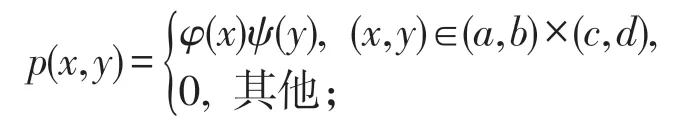
由定理1,X,Y相互獨立。
(必要性)當X,Y相互獨立時,有
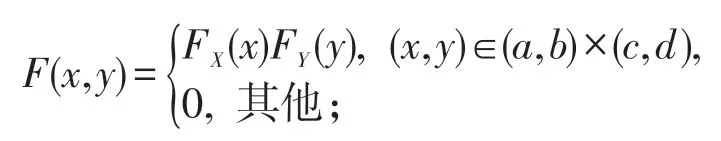
其中FX(x),FY(y)分別為X,Y的邊際分布函數。令f(x)=FX(x),g(y)=FY(y) ,即 知F(x,y)=f(x)g(y) ,(x,y)∈D= (a,b)×(c,d),即定理 2 中的條件(1)、(2)成立。
注2:定理2 條件(1)中,分解式F(x,y)=f(x)g(y)不具有唯一性。
2 應用
定理1、定理2 的優點在于在實際問題的判斷中,我們不必先由聯合密度函數p(x,y)求出pX(x) ,pY(y),然后再看是否有p(x,y)=pX(x)pY(y);或不必先由聯合分布函數F(x,y)求得FX(x),FY(y),再驗證是否有F(x,y)=FX(x)FY(y),那樣做將是比較麻煩的。而應用定理1、定理2,我們可直接觀察p(x,y) 或F(x,y)的形態和D的形狀,直接對p(x,y)或F(x,y)進行分解、判斷,這就節省了時間和精力。下面試舉兩例,說明定理1、定理2 的應用,從中讀者也可看到定理1、定理2的優點。
例1 設二維隨機變量(X,Y)的聯合密度函數如下,試問X與Y是否相互獨立?

解:(1)設φ(x)=xe-x,ψ(y)=e-y,則
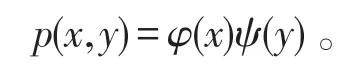
又 設a=0,b=+∞,c=0,d=+∞,則D=(0,+∞)×(0,+∞)=[(a,b)×(c,d)],說明定理1中的條件(1)、(2)均滿足,故X,Y相互獨立。
(2)雖然我們可取φ(x)=24x,ψ(y)=y,p(x,y)=φ(x)ψ(y),定 理 1 中 條 件(1)成 立 。 但D= {(x,y)|0 <x,y<1,0 <x+y<1}無法表成 (a,b)×(c,d)的形式,說明x,y的取值相互影響,故X,Y不相互獨立。
例2 設二維隨機變量(X,Y)的聯合分布函數如下,試問X與Y是否相互獨立?
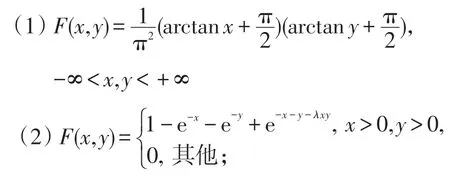
其中參數λ>0。
解:(1)令
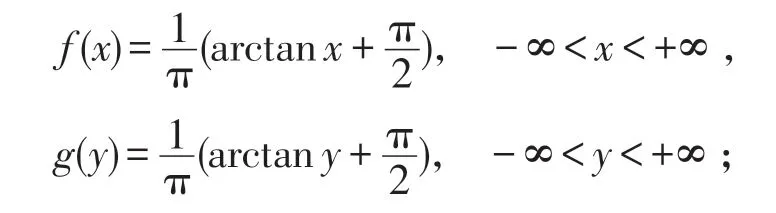
則定理2中條件(1)、(2)滿足,故X與Y相互獨立。
(2)雖然D=(0,+∞)×(0,+∞) ,定理 2 中的條件(2)滿足;但F(x,y) 無法表成F(x,y)=f(x)g(y) 的形式,定理2中條件(1)不滿足,故X,Y不相互獨立。
3 結果的推廣
把定理1 的結果進行推廣,就可得到下面定理3。
定理3 設n維連續隨機變量(X1,X2,…,Xn)的聯合密度函數為p(x1,x2,…,xn),(x1,x2,…,xn)∈D,D為Rn中的區域;其余,p(x1,x2,…,xn)=0 ,則X1,X2,…,Xn相互獨立的充要條件是:
(1)p(x1,x2,…,xn)=φ1(x1)φ2(x2)…φn(xn),
(2)D=(a1,b1)×(a2,b2)×…×(an,bn),
其中φi(xi) 為 (ai,bi) 上的可積函數,i=1,2,…,n;ai,bi為實數,ai可為-∞,bi可為+∞,i=1,2,…,n。
定理3的證明略,可參照定理1的證明完成。
把定理2 的結果進行推廣,就可得到下面定理4。
定理4 設n維連續隨機變量(X1,X2,…,Xn)的聯合分布函數為F(x1,x2,…,xn),(x1,x2,…,xn)∈D,D為Rn中的區域;其余,F(x1,x2,…,xn)=0 ,則X1,X2,…,Xn相互獨立的充要條件是:
(1)F(x1,x2,…,xn)=f1(x1)f2(x2)…fn(xn),
(2)D=(a1,b1)×(a2,b2)×…×(an,bn),
其中fi(xi) 為 (ai,bi) 上的可導函數,i=1,2,…,n;ai,bi為實數,ai可為-∞,bi可為+∞,i=1,2,…,n。
定理4的證明略,可仿照定理2的證明完成。
〔1〕茆詩松,程依明,濮曉龍. 概率論與數理統計〔M〕. 2 版.北京:高等教育出版社,2014.
〔2〕李裕奇,趙刊.n維隨機變量獨立性的一個充要條件〔J〕.西南交通大學學報,1998,33(5):513-517.
〔3〕驕俊生,張德然.關于二維連續型隨機變量獨立性的判斷〔J〕.工科數學,1995,11(2):101-104.
〔4〕劉國旗.關于二元隨機變量獨立性的判定條件〔J〕.安徽建筑工業學院學報:自然科學版,2001,9(2):76-78.
〔5〕佟毅.關于隨機變量獨立性的研究〔J〕.石油化工高等學校學報,1994,7(3):71-74.
〔6〕姚仲明,唐燕玉. 隨機變量的獨立性及其一個充要條件〔J〕. 安慶師范學院學報:自然科學版,2004,10(4):71-73.
〔7〕佟毅.隨機向量獨立性的一個充要條件〔J〕.工科數學,1995,11(1):54-57.
〔8〕傅自晦.關于正態隨機變量的獨立性與相關性〔J〕.工科數學,1998,14(2):141-143.
〔9〕趙海燕,謝成康.連續型隨機變量相互獨立的密度函數等價條件〔J〕.大學數學,2011,27(2):153-155.
〔10〕魏志道.Fuzzy 隨機變量的獨立性〔J〕.四川師范大學學報:自然科學版,1994,17(5):18-23.

