基于雙目視覺的機器人位姿標定技術研究

吳年祥，殷蔚民，鄒華東

（1.中國地質大學自動化學院，武漢 430074；2.安徽國防科技職業學院機電工程系，安徽六安 237001）

隨著工業技術的迅速發展，機器人技術在機械、機電、汽車、電子等行業發揮著重要角色。在柔性自動生產線中，機器人機械手的抓取、放置、裝配、焊接等應用最廣泛。然而，產品競爭日益激烈，產品質量的不斷提高要求工業機器人能在機電一體化等生產中完成三維空間精確操作，而基于視覺的機器人外部位姿標定技術的研究也顯得尤為重要。機器人外部位姿是指確定機器人世界坐標系和基礎坐標系及工件坐標系之間的關系〔1〕。而在機器人基坐標系固定情況下，通常將其與世界人坐標系設置重合，從而確定機器人基坐標系與工件坐標系之間的坐標變換關系即機器人外部位姿。本文通過分步標定法之一的機器人外部位姿來確定機器人工件坐標系與基坐標系之間的坐標變換關系，從而確定機器人工件坐標系與立體視覺傳感器坐標系之間的關系〔2〕。

1 機器人雙目立體視覺傳感器的三坐標數學模型

機器人雙目立體視覺在計量測量技術領域的作用充分體現靈活的運動性、通用性。通過安裝在機器人末端手關節上的左右放置的雙目激光立體視覺傳感器獲取空間點的三維信息。其雙目立體視覺測量示意圖如圖1 所示，數學模型如圖2 所示。被測工件與末端關節左右相對固定的立體視覺傳感器構成三角形，被測工件在兩臺攝像機上呈現立體圖像對，匹配相關的特征點，采用最小二乘法，計算左右兩幅圖像的視覺差異獲得空間特征點的三維坐標位置。

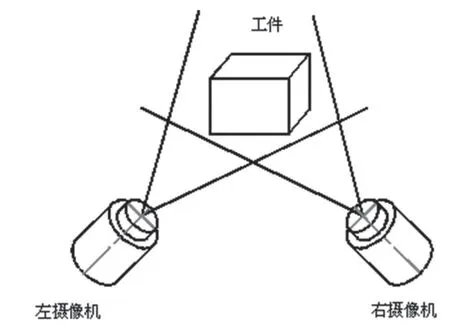
圖1 雙目立體視覺傳感器測量示意圖

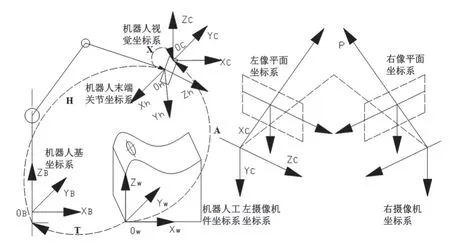
圖2 機器人外部位姿標定與視覺傳感器測量模型圖

左、右兩個相對位置固定的視覺傳感器所處的空間關系如式（1）所示：

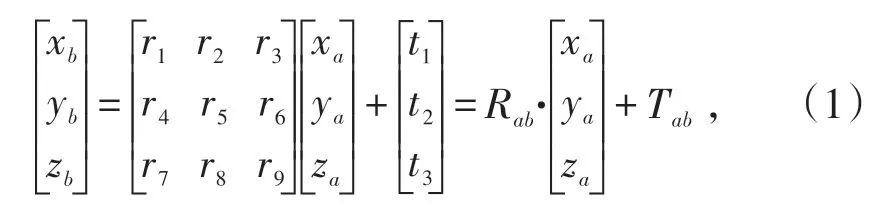
其中視覺傳感器的兩個外部參數：左、右相對位置攝像機坐標系間的平移矢量與旋轉矩陣分別用Tab和Rab來表示。聯立式（1）中的（xb，yb，zb）3 個方程，利用最小二乘算法求解該式，可以獲得視覺傳感器坐標系下空間特征點的三維坐標位置：

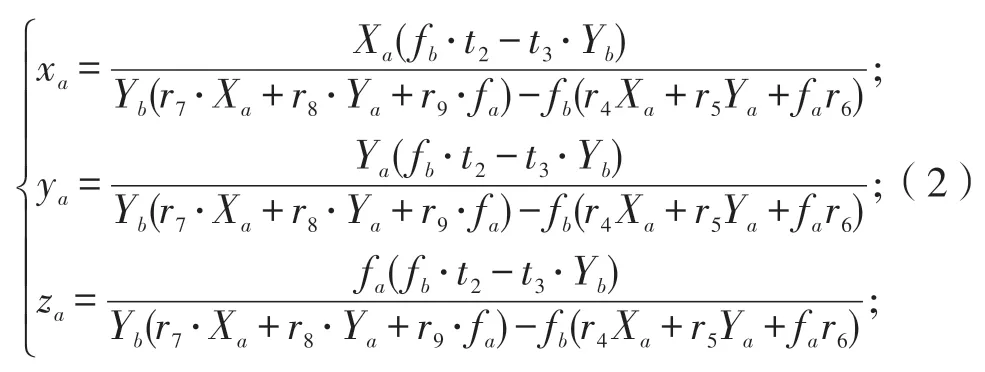
式（2）右邊的固定參數可以通過攝像機傳感器內部與外部參數的標定方法獲得〔3〕。因此，在雙目立體視覺傳感器下，以上數學模型的建立可以獲得空間被測點三維位置的信息（xa，ya，za）T。通過機器人手眼關系和靶標法可以間接得出空間任意有效被測點時，機器人工件坐標系和視覺傳感器坐標系之間的坐標變換關系。

2 機器人外部位姿標定方式

2.1 機器人位姿方程的建立與求解方法如圖2所示，按照Shiu 等〔4〕手眼標定算法以及機器人系統坐標變換鏈的閉合特征，用矩陣A 來表示工件坐標和視覺傳感器件坐標系之間的位置關系，矩陣T 表示工件坐標系和機器人基坐標系之間的位置關系，未知位置關系X表示視覺傳感器坐標系與機器人末端關節坐標系之間的齊次坐標變換矩陣，矩陣H表示機器人基坐標系相對于機器人末端關節的位姿，再經過機器人視覺傳感器坐標系到末端關節坐標系以及基坐標系的齊次坐標相關變換X·H，可以將任意空間位置點的坐標統一轉換至基坐標系下〔5〕。

由圖2 可知，該位姿標定坐標變換鏈的閉合特征，可以得出：

通過先求解工件坐標和視覺傳感器坐標系之間的位置矩陣關系A，可以求解矩陣T。由式（4）齊次矩陣坐標方程的變換，可以將經過標定后的視覺傳感器特征點的空間三維坐標值轉移到工件坐標系下。如果空間有若干個點Pi(i≥4)，經過其空間點的齊次坐標相關變換H·X，可以由在其工件坐標系下的坐標位置（xi，yi，zi）T轉換為基坐標系下的坐標位置（xBi，yBi，zBi）T。

假設：

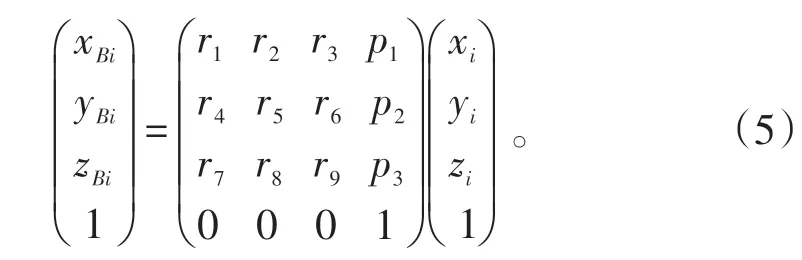
式（5）中

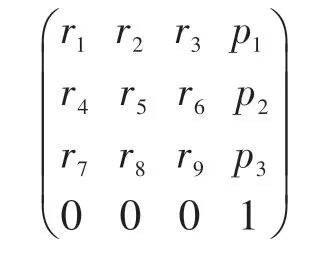
就是所求機器人外部位姿T，即工件坐標系和機器人基坐標系之間的位置關系，而T矩陣中的

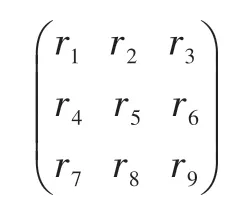
旋轉子矩陣依據正交約束方式建立方程為非線性，求解困難。為簡化方程，使用坐標空間多點采集方法，確立線性方程求解。

對于一個空間點可以列出3 個位置方向方程，假設有4 個已知點的坐標值（p1，p2，p3，p4）分別代入式（5），可以得出矩陣A 中的12 個不相關的未知量方程：將式（6-1）、（6-2）、（6-3）、（6-4）合并轉換成矩陣形式，可以得到式（9）：

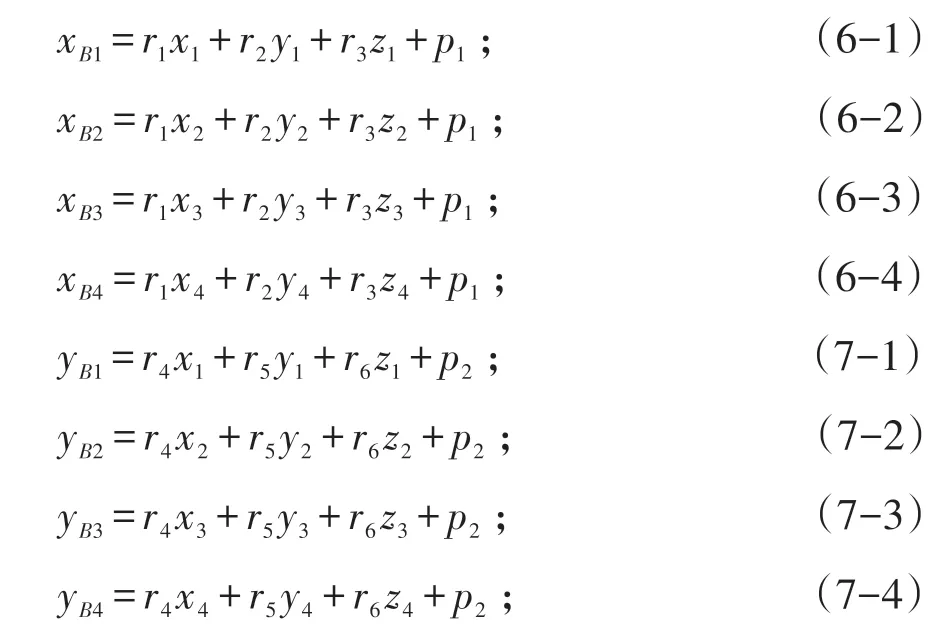
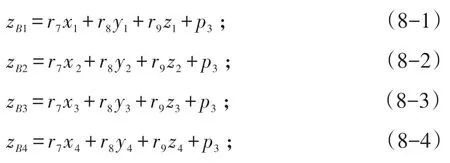
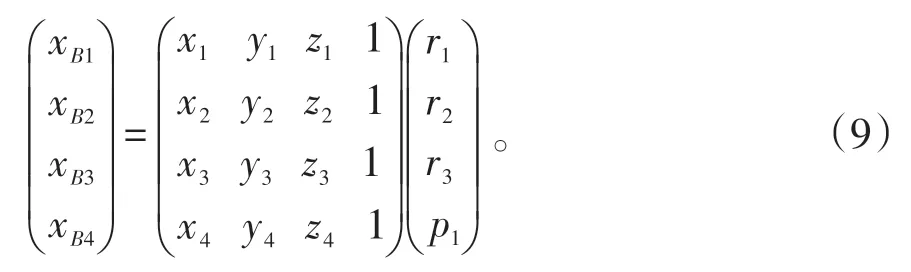
將式（9）的四元一次方程組利用高斯消去法（Gaussian Elimination）可以直接求解得到未知數：r1、r2、r3、p1。同理可以將式（7-1）、（7-2）、（7-3）、（7-4）和（8-1）、（8-2）、（8-3）、（8-4）合并轉換成矩陣形式，可以得到（10）、（11）：

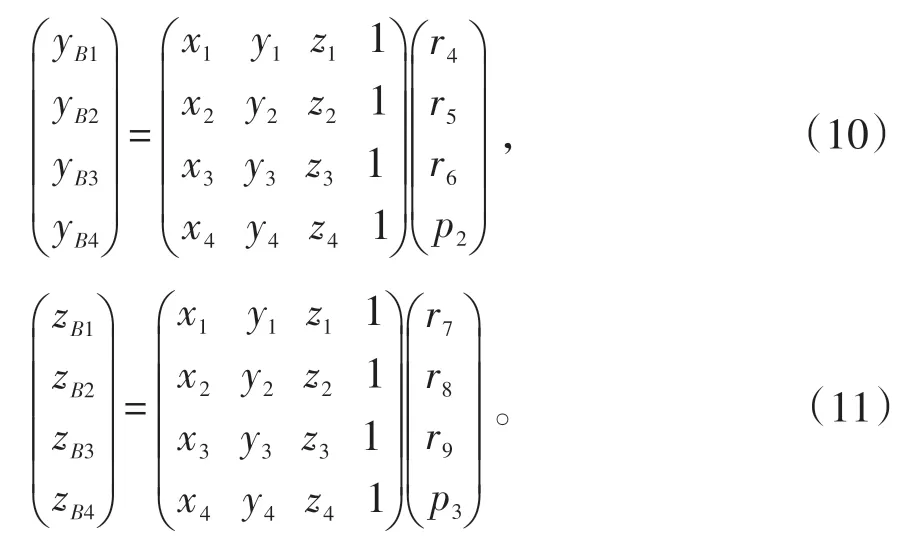
同理，再通過高斯消去法求解 r4、r5、r6、p2和 r7、r8、r9、p3矩陣。進而求得機器人外部位姿工件坐標系與機器人基坐標系之間的位置關系矩陣T。

在實際應用當中，考慮各種坐標系下的坐標值存在噪聲誤差，進一步提高精度問題，可進一步采用最小二乘法擬合，將方程組（9）、（10）、（11）簡化成D=C·Y矩陣方程形式：

式（12）為每一個方程組所對應的未知量向量，也同樣可以得出機器人的外部位姿。

2.2 機器人外部位姿的工具與標定方式通過以下靶標法來確定機器人在某一位姿時工件坐標系和機器人視覺傳感器坐標系之間齊次坐標變換矩陣A。如圖3，首先讓機器人固定在某一靜態位姿，其次利用CMM（三坐標測量機）標定一個定位夾，可以得到其夾具坐標系和靶標坐標系之間的精確位置關系，最后將圓形平面靶標定位安裝到工件坐標系范圍內，并且讓其工件定位基準和夾具定位基準重合，從而保證它們之間的坐標系重合。

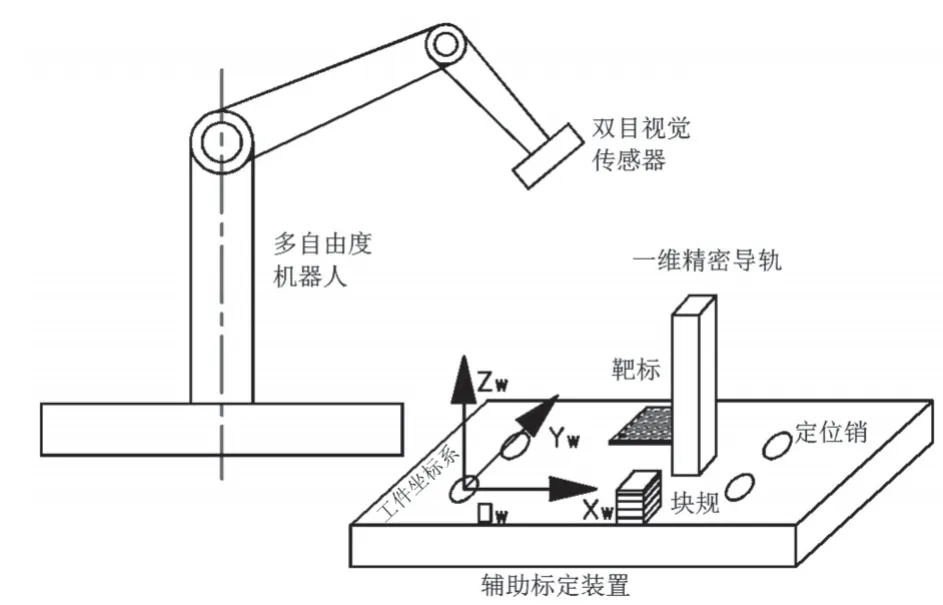
圖3 靶標法示意圖

在測量當中，圓形平面的靶標配合一維精密導軌和組合量塊的使用，使靶標能夠在視覺傳感器的可視范圍內移動，從而可以采集更多的空間已知坐標點。經過已標定的工件坐標系和靶標坐標系的關系，從而得出視覺傳感器所采集到的空間特征點在工件坐標系下的坐標值也是已知的，再利用“2.1”機器人位姿方程的建立與求解方式可以得出齊次坐標變換矩陣A。綜上所述知該靶標法利用了機器人在某一靜態位姿時的相關值進行了機器人在任意狀態時都固定不變的機器人外部位姿的求解〔6〕。

3 模擬研究實驗

本實驗采用模擬實驗方法來初步驗證基本立體視覺的機器人位姿標定程序設計算法的測量精度。

假設機器人實際外部位姿其中的一組數據矩陣為：

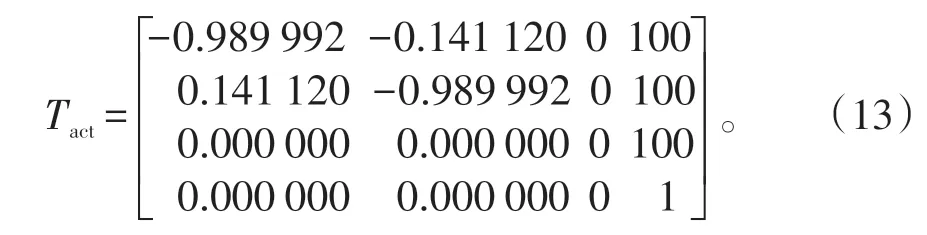
并假定，位于工件坐標系下4 個位置點（p1，p2，p3，p4）的坐標值分別為（1.5，2.0，3.3）T，（30.2，-5.7，8.9）T，（102.4，70.7，59.8）T，（-40.6，89.9，-50.4）T分別代入式（5），通過矩陣整理和運算可以得出在機器人基礎坐標系下4 個位置點的坐標值分別為：（98.2328，97.8083，103.3）T，（70.9066，101.381，108.9）T，（-11.352 4，15.556 9，159.8）T，（127.507，16.729 2，49.8）T。見圖4。

圖4 外部位姿標定求解

將上述位于機器人基坐標系與工件坐標系下4個點的坐標值輸入程序，得出機器人外部位姿計算結果：

外部位姿模擬實驗結果見圖5。

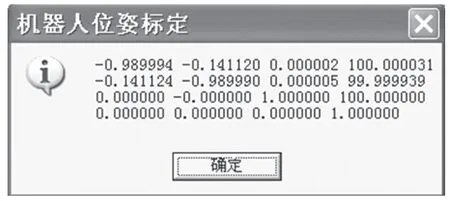
圖5 外部位姿模擬實驗結果

從假設的真值式（13）與計算結果式（14）可以看出，其數據誤差在10-5數量級上。同理，若在數據不存在噪聲因素的情況下，進行大量仿真實驗進行推論，其系統精度級別高。

4 結論

本文建立雙目立體視覺傳感器三坐標的數學模型，得出空間特征點的三維坐標。通過機器人外部位姿工具與靶標法利用了機器人在某一靜態位姿時的相關值進行了機器人在任意狀態時都固定不變的機器人外部位姿的求解。仿真實驗表明，在沒有噪聲因素的環境中，此方法可以獲得機器人外部位姿的精確求解。

〔1〕周富強.CCD 攝像機快速標定技術〔J〕.光學精密工程，2002，8（1）：97-99.

〔2〕楊濤.基于合作靶標的激光掃描車身坐標測量關鍵技術研究〔D〕.天津：天津大學，2009：6-7.

〔3〕楊劍，呂乃光，董明利.加權最小二乘算法在機器視覺系統中的應用〔J〕. 光學精密工程，2009，17（8）：1871-1873.

〔4〕Shiu Y C，Ahmad S. Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX=XB〔J〕.IEEE Transactions on Robotics&Automation，1989，5（1）：16-29.

〔5〕鄭俊，邾繼貴，葉聲華.基于雙目立體視覺的機器人測量技術研究〔J〕.計量技術，2005，17（4）：15-17.

〔6〕鄭俊. 基于立體視覺的通用測量機器人標定模式研究〔D〕.天津：天津大學，2005：25-29.