降雨條件下土質(zhì)高邊坡穩(wěn)定性影響因素分析

秦 帥 丁 涯

(1.重慶交通大學土木建筑學院，重慶 400074； 2.中建八局第三建筑有限公司，重慶 400010)

降雨條件下土質(zhì)高邊坡穩(wěn)定性影響因素分析

秦 帥1丁 涯2

(1.重慶交通大學土木建筑學院，重慶 400074； 2.中建八局第三建筑有限公司，重慶 400010)

選取影響土質(zhì)高邊坡穩(wěn)定性的指標，采用變量控制的方法，在ABAQUS軟件中分別計算了各個指標不同數(shù)值情況下的穩(wěn)定系數(shù)，并利用改進的灰色關聯(lián)分析法計算出土質(zhì)高邊坡穩(wěn)定性對各個因子的敏感性，為以后的邊坡工程設計和施工提供一定的參考。

降雨，土質(zhì)高邊坡，穩(wěn)定，灰色關聯(lián)度

土質(zhì)高邊坡作為一種普遍存在的地質(zhì)體，其穩(wěn)定性受到諸多因素的影響。不管是自然形成的高邊坡還是人工修筑的高邊坡，降水都是誘發(fā)邊坡失穩(wěn)的重要因素。由于降雨存在著諸多的不確定性，因此，對于降雨引發(fā)土質(zhì)高邊坡失穩(wěn)的一般規(guī)律的研究，長久以來多采用歸納統(tǒng)計的方法。歸納統(tǒng)計的方法具有一定的盲目性，無法排除一些偶然因素的影響。計算機技術的急速發(fā)展，包括計算能力的突飛猛進和大型有限元軟件的日趨完善，為用數(shù)值模擬方法模擬邊坡失穩(wěn)提供了必要的基礎。相對而言，數(shù)值模擬方法具有較大的優(yōu)勢。

本文試運用灰色關聯(lián)度評價方法，對降雨條件下土質(zhì)高邊坡失穩(wěn)的影響因素進行敏感性分析計算，并對其影響權重進行比較和排序。

1 土質(zhì)高邊坡穩(wěn)定性影響因素剖析

邊坡的失穩(wěn)從根本上來講，是力的平衡關系被打破之后，其自身調(diào)整至新的平衡的過程。土質(zhì)高邊坡是一個極其復雜的系統(tǒng)，影響因素復雜而眾多，但歸根結(jié)底，仍可以分為兩大類，即內(nèi)在因素和外在因素。

1.1 內(nèi)在因素

內(nèi)在因素是指能夠影響其穩(wěn)定性的土體自身所具有的特點，或其所處地質(zhì)環(huán)境的特點，包括：邊坡巖土體的地層、土質(zhì)、巖土體的結(jié)構面、地下水的作用和邊坡的形態(tài)與規(guī)模等。

1.2 外在因素

影響邊坡穩(wěn)定的外在因素大致可以分為自然因素和人為因素兩個方面。自然因素是指在公路工程所賦存的自然環(huán)境中，對邊坡穩(wěn)定性有重要影響的偶發(fā)或常發(fā)自然現(xiàn)象，主要有降水作用、地震作用和風化作用等。人為因素是指人類在改造自然的過程中，不可避免的對邊坡產(chǎn)生的影響。雖然人為因素在邊坡失穩(wěn)的誘因中屬于次要因素，但任何可能的因素都必須引起足夠的重視。

2 降雨條件下土質(zhì)高邊坡穩(wěn)定性影響因素分析

人們在對復雜系統(tǒng)進行系統(tǒng)分析時，以往大多采用統(tǒng)計分析或其他分析方法，然而這些分析方法都或多或少的存在一些問題，如要求樣本量足夠大、計算量較大、分析結(jié)果不夠可靠等。

1982年，鄧聚龍教授提出了灰色系統(tǒng)理論，這是一種運用全新方法描述信息不完全的系統(tǒng)并進行預測、決策、控制的系統(tǒng)理論。灰色關聯(lián)分析是灰色系統(tǒng)理論的主要內(nèi)容之一，它可以對物理機制不明確，甚至缺乏物理原型的因果之間建立使其顯化、量化和序化的數(shù)學模型，為復雜系統(tǒng)的建模和分析提供依據(jù)的重要分析手段。

本文擬采用灰色關聯(lián)分析法進行降雨條件下土質(zhì)高邊坡穩(wěn)定性影響因素分析。

2.1 灰色關聯(lián)分析基本方法

2.1.1 確定數(shù)據(jù)矩陣

首先指定影響系統(tǒng)行為的矩陣X，同時指定矩陣X中相應元素的參考值，一般為相應元素與標準值或臨界值的比值，組成比較矩陣Y。

(1)

(2)

2.1.2 矩陣無量綱化

考慮到各影響因素之間單位互不相同，數(shù)量級也可能有較大的差別，放在一起無法進行比較，因此有必要對矩陣進行無量綱化處理。此處選用區(qū)間相對值變換，方法如下：

(3)

(4)

2.1.3 求差值矩陣

(5)

并求出最大最小值。

Δ(max)=max(Δij)

(6)

Δ(min)=min(Δij)

(7)

2.1.4 關聯(lián)度矩陣與關聯(lián)度

灰色關聯(lián)分析方法的基本原理是通過對統(tǒng)計序列幾何關系的比較來分清系統(tǒng)中多因素的關系的緊密程度。序列曲線的幾何形狀越接近，則它們的關聯(lián)度就越大，反之則越小。因此將曲線之間的差值作為關聯(lián)度的衡量指標，比較因素同參考因素的相關性用關聯(lián)系數(shù)表示。

(8)

其中,ξ為分辨系數(shù)，ξ∈(0，1),通常取ξ=0.5。

關聯(lián)度按下式計算：

(9)

其中，wj為各個因素的權重。

關聯(lián)度的值域在[0,1]之間變化，關聯(lián)度越接近1，則說明結(jié)果相對應的參考數(shù)列越敏感，反之，越不敏感。

2.1.5 權的計算

由于各個影響因素在實際中的地位并不一樣，因此有必要引入權，來使計算結(jié)果更貼近現(xiàn)實。本文采用距離分析法來計算權。

1)原始數(shù)據(jù)。

此處將關聯(lián)度矩陣作為原始矩陣。記A=Zij。

(10)

2)同向化指標。

將逆指標轉(zhuǎn)化為正指標，轉(zhuǎn)化后的數(shù)據(jù)矩陣仍記為A。

3)數(shù)列矩陣無量綱化。

采用比重法消除原始數(shù)據(jù)的量綱，得到新的矩陣B。

(11)

4)確定樣本最優(yōu)最劣值。

選取矩陣B中各指標的極大極小值分別構成最優(yōu)樣本和最劣樣本，分別用B+，B-表示。

(12)

(13)

5)計算各樣本點到參考樣本點的距離。

(14)

(15)

6)計算各樣本點到最優(yōu)樣本點的相對接近度：

(16)

7)對Ck作歸一化處理，得關聯(lián)度權重向量值。

(17)

則w=(w1,w2,…,wm)T即為權重向量。

2.2 影響因素敏感性分析

本文將以基本邊坡形式為例，選取降雨強度、降雨持時、重度、有效粘聚力、有效內(nèi)摩擦角、坡度、坡高、飽和滲透系數(shù)這8個影響因子作為研究對象進行敏感性分析。通過變量控制的方法，分別控制這8個影響因素的變化，得到不同情況下的工況，并利用ABAQUS有限元軟件對此時的邊坡穩(wěn)定性進行驗算，得出相應的安全系數(shù)，結(jié)果如表1所示。

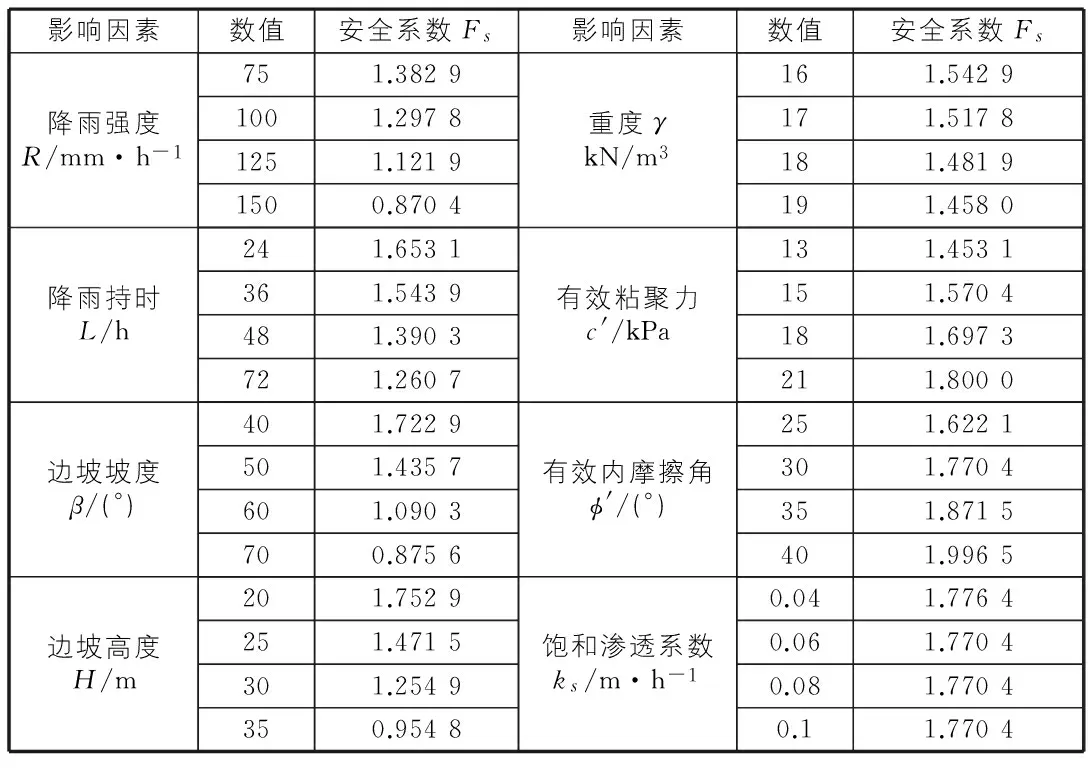
表1 影響因素和安全系數(shù)

根據(jù)表1中提供的數(shù)據(jù)，建立比較矩陣和參考矩陣。比較矩陣：

(18)

參考矩陣：

(19)

消除參考矩陣的量綱，得到灰色關聯(lián)系數(shù)矩陣：

(20)

將灰色關聯(lián)矩陣Z作為原始數(shù)據(jù)矩陣A，無量綱化后得到數(shù)據(jù)矩陣B：

(21)

從數(shù)據(jù)矩陣B中選取最優(yōu)最劣樣本：

B+=(0.732 80.730 50.641 50.632 60.615 10.536 90.570 60.685 6)T

(22)

B-=(0.330 20.326 20.354 00.333 40.357 20.456 50.361 00.380 9)T

(23)

計算各樣本點到參考樣本點的距離：

D+=(0.810 60.354 30.302 30.810 6)T

(24)

D-=(0.224 50.625 20.735 00.224 5)T

(25)

計算相對接近度：

Ck=(0.216 90.638 30.708 60.216 9)T

(26)

對Ck作歸一化處理，得到權重向量：

w=(0.121 80.358 40.397 80.121 8)T

(27)

最后計算得到關聯(lián)矩陣：

(28)

根據(jù)式(9)計算關聯(lián)度，結(jié)果如表2所示。

表2 降雨條件下邊坡穩(wěn)定性影響因素關聯(lián)度

從表2中可以看出，在降雨條件下影響邊坡穩(wěn)定性的影響因素敏感性排序：c′>φ′>L>R>H>β>γ>ks。

3 結(jié)語

降雨條件下土質(zhì)高邊坡的穩(wěn)定性主要受三個方面的影響，即土質(zhì)自身的物理力學特性、坡體的規(guī)模與形態(tài)和降雨條件這三大影響因素。其中，土質(zhì)自身的物理力學特性幾乎起到了決定性的作用，土體的有效粘聚力和有效內(nèi)摩擦角兩項指標的關聯(lián)度分別高達0.891 5和0.789 3。滲透系數(shù)對邊坡穩(wěn)定性的影響最小。其余幾項指標的關聯(lián)度則相差不大，但降雨條件下，降雨持時和降雨強度也是影響邊坡穩(wěn)定的重要因素。因此，邊坡在設計和施工時，必須重視降雨的影響，按照規(guī)范的要求設置相應的截水、排水設施，個別復雜的情況下須特殊設計，并謹慎驗算，確保邊坡穩(wěn)定。

[1] 張正雄，張福明，陳玉鳳.山區(qū)高等級公路邊坡失穩(wěn)原因分析與對策[J].林業(yè)建設，2004(4)：34-37.

[2] 丁繼新，尚彥軍，楊志法.降雨型滑坡預報新方法[J].巖石力學與工程學報，2004，23(21)：3738-3743.

[3] Dai F C．Lee C F．Frequency-volume relation and prediction of rainfall-induced landslides[J]．Engineering Geology，2001(59)：253-266．

[4] 張 珍，李世海，馬 力.重慶地區(qū)滑坡與降雨關系的概率分析[J].巖石力學與工程學報，2005，24(17)：3185-3191.

[5] Alonso E，Gens A，Lioret A．Effect of Rain Infiltration on the Stability of Slopes[J]．Unsaturated Soils，1995(1)：241-249．

[6] 林孝松.滑坡與降雨研究[J].地質(zhì)災害與環(huán)境保護，2001，12(3)：1-7．

[7] 林鴻州，于玉貞，李廣信.降雨特性對土質(zhì)邊坡失穩(wěn)的影響[J].巖石力學與工程學報，2009，28(1)：198-204．

[8] 姚愛軍，薛廷河.復雜邊坡穩(wěn)定性評價方法與工程實踐[M].北京：科學出版社，2008.

[9] 曹明霞.灰色關聯(lián)分析模型及其應用的研究[D].南京：南京航空航天大學,2007：7-21.

[10] 劉思峰，黨耀國，方志耕.灰色系統(tǒng)理論及其應用[M].北京：科學出版社，2005.

On analysis of influential factors for high soil slope stability under rainfall condition

Qin Shuai1Ding Ya2

(1.CivilEngineeringCollege,ChongqingCommunicationUniversity,Chongqing400074,China;

2.No.3ArchitecturalCompany,ChinaConstruction8thBureau,Chongqing400010,China)

The paper selects the indexes which affect the high soil slope stability, adopts the variable controlling method, calculates the stability coefficients with various numbers with ABAQUS software, and adopts the improved gray relational analysis method to calculate the sensibility of the factors of the high soil slope, so as to provide some reference for the slope engineering design and construction in future.

rainfall, high soil slope, stability, gray relation

1009-6825(2015)02-0056-03

2014-11-10

秦 帥(1989- )，男，在讀碩士； 丁 涯(1988- )，男，助理工程師

TU413.62

A