基于機會約束凸松弛的分區隨機無功備用優化方法

方斯頓 程浩忠 馬紫峰 宋 越 張 健 李柏青

(1.電力傳輸與功率變換教育部重點實驗室(上海交通大學) 上海 2002402.香港大學電機工程系 香港3.中國電力科學研究院系統所 北京 100192)

?

基于機會約束凸松弛的分區隨機無功備用優化方法

方斯頓1程浩忠1馬紫峰1宋 越2張 健3李柏青3

(1.電力傳輸與功率變換教育部重點實驗室(上海交通大學) 上海 2002402.香港大學電機工程系 香港3.中國電力科學研究院系統所 北京 100192)

針對含不確定性的新能源大量接入和系統無功功率的區域特性，提出一種基于電壓控制分區的區域隨機無功備用優化方法。首先采用基于凝聚聚類和模塊度指標對系統進行無功分區，然后利用松弛方法將含隨機性的優化模型轉換為確定型，最后提出基于無功分區的逐次無功備用優化方法。若干仿真算例的分析證明，機會約束凸松弛方法可較準確地轉換機會約束，而分區優化方法將高維的無功備用問題轉換為低維的子問題，提高了算法的尋優效率，獲得的優化方案可顯著提高區域無功備用和電壓穩定裕度，降低系統運行的風險，并對N-1故障后系統的電壓水平也有一定改善作用。

機會約束凸松弛 無功控制分區 無功備用 逐次分區優化 電壓穩定裕度

0 引言

發電機無功備用對維持電力系統的穩定運行具有重要意義[1]，對其進行優化可有效改善系統的安全水平。目前，無功備用容量主要有物理備用[2]和有效備用[3]兩種方式，而由于有效備用能夠更準確地衡量發電機的無功支撐能力，在實際中應用更加廣泛。隨著安裝位置不同，不同發電機無功備用的價值也不盡相同，有必要將總無功備用定義為單臺發電機無功備用的加權和。文獻[4]采用節點無功參與因子定義無功備用權系數，但其僅適用于鞍結分岔類型(Saddle Node Bifurcation，SNB)，不適合于極限誘導分岔類型(Limit Induced Bifurcation，LIB)。文獻[5]指出極限曲面法矢量能夠指示LIB時節點電壓的薄弱性，但由于極限曲面的復雜性，法矢量指標在某些區域可能變化較劇烈，不適合單獨使用。此外，由于無功功率的區域特性，發電機無功備用對電氣距離較遠的節點支撐能力較弱[5]，因此合理地對電力系統進行分區并確定薄弱區域，進而僅對薄弱區域進行無功備用優化可在保證系統電壓水平的情況下大幅度提升算法效率。

隨著以風能為代表的可再生能源大量接入，節點注入功率的隨機性日益明顯，目前在無功備用優化領域，考慮隨機性的模型還未見報道。但眾多研究表明，在含不確定性的系統中直接應用確定型模型會增加系統的運行風險。因此，在無功備用優化模型中考慮隨機性是值得嘗試的研究思路。目前，含多隨機變量的優化問題求解方法主要有區間數法[6]、魯棒優化[7，8]、模糊規劃[9]及機會約束規劃[10]等。區間數方法需給定隨機變量概率分布函數，在實際中很難獲得；魯棒優化把含隨機性的問題轉換為兩層問題求解，結果偏保守；模糊規劃在應用于復雜系統時難以定義合適的隸屬度函數；而機會約束則由于其簡單直觀得到廣泛應用。但機會約束一般不滿足凸性條件，因此很難直接采用經典算法進行求解，目前主要的求解方法包括智能算法[11-14]和松弛方法[15]。智能算法對優化模型的凸性要求不高，且全局搜索能力強，但計算效率低，很難應用于調度問題。松弛方法首先將機會約束轉換為確定型，進而采用經典算法進行求解，所得結果是原優化問題的下界(或上界)，通過檢驗后即得到原問題的解。

本文提出一種基于機會約束凸松弛的分區隨機無功備用優化方法，該方法不僅能提升系統的電壓穩定裕度，而且考慮隨機性的影響，降低系統的運行風險，仿真實例證明本文方法對N-1故障后的電壓水平也有顯著提升作用。

1 基于模塊度指標的無功分區

1.1 發電機與節點的電氣距離

電力系統潮流方程為

(1)

對等式兩邊進行微分

(2)

消去與有功、相角相關的量，可得到系統無功與節點電壓的關系

(3)

因此，可得到系統無功源對節點的控制靈敏度為

(4)

式中：G為無功源指標集；L為受控節點指標集；ΔQG為無功源的出力變化量；ΔVL為受控節點電壓的變化矢量；SLG為控制靈敏度矩陣。

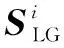
(5)

由此可定義分區s、t之間的距離為

(6)

式中Gs、Gt分別為各自分區中的無功源指標集。

1.2 基于凝聚聚類和模塊度的無功分區

1.2.1 模塊度指標

根據文獻[16]定義的加權有向圖模塊度衡量分區方案的解耦程度，模塊度指標定義為

(7)

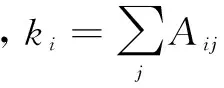
合理地分區應使區域內部的電氣距離近，而與區域外的距離遠，基于文獻[17]的定義，根據節點的不同類型定義電氣距離為

(8)

(9)

式中：dij為節點i、j的電氣距離；yij為節點i、j之間的導納值。若i為受控節點，αij為節點j電壓單位變化時節點i電壓變化量；若i為無功源節點，其電壓不變化，αij為節點j無功單位變化時節點i無功出力變化量。

1.2.2 無功分區步驟

根據上文定義的指標，采用分層無功分區算法，流程如圖1所示。

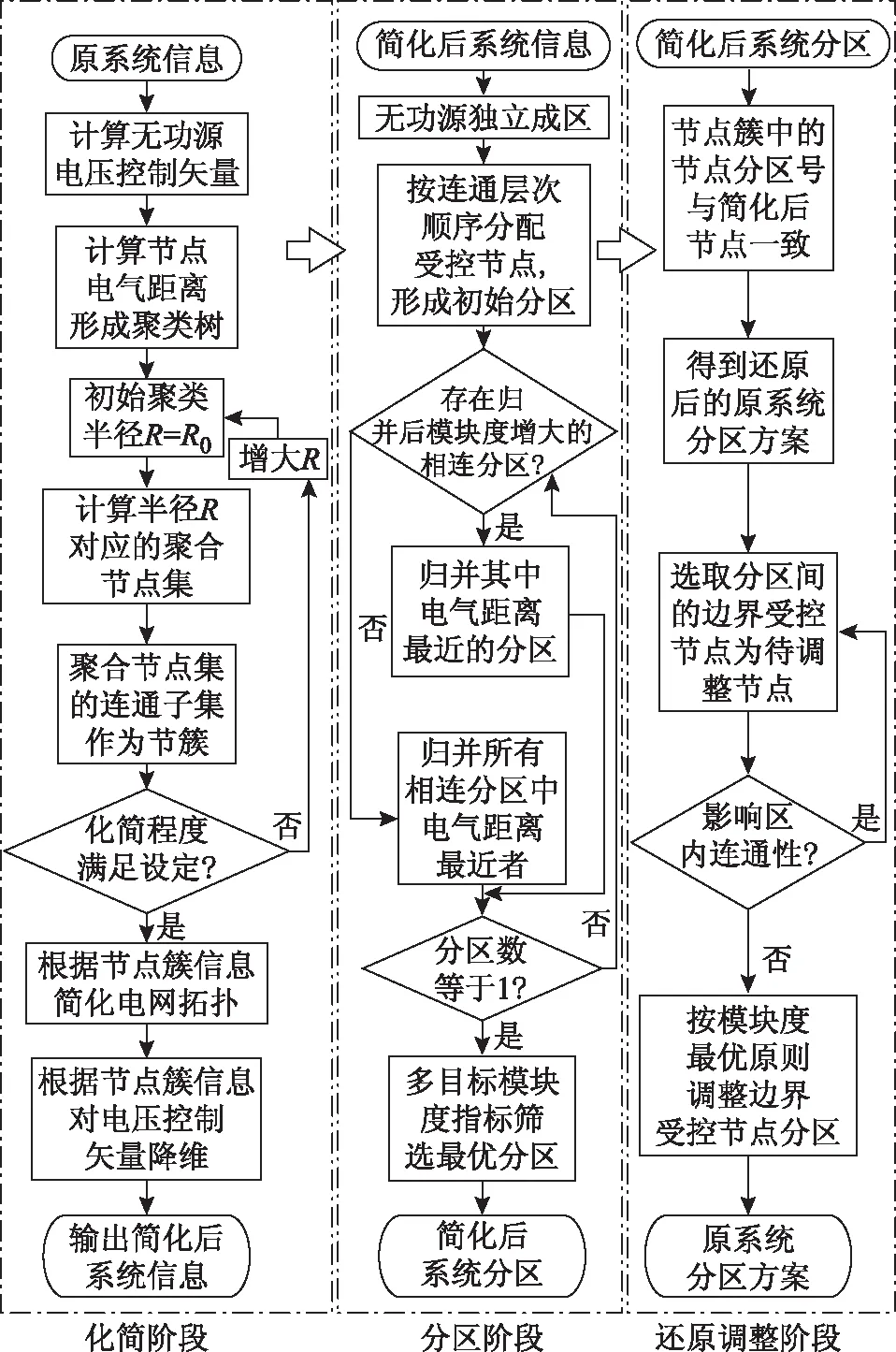
圖1 多層次分區算法流程Fig.1 Flow chart of the multi-level partitioning algorithm

2 考慮隨機性的無功備用優化模型

2.1 發電機無功備用權系數定義

文獻[4]指出節點參與因子可很好地表征SNB失穩模式下節點電壓的薄弱性，但卻無法應用于LIB情況。文獻[5]指出利用極限曲面法向量指標可衡量SNB和LIB情況下的節點電壓薄弱性，但該指標依賴于固定的負荷增長方向。因此，結合兩個指標，提出新的無功備用權系數為

(10)

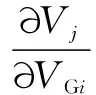
2.2 分區無功備用優化模型

1)分區k的無功備用為

(11)

2)變量約束為

(12)

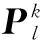
3 基于機會約束松弛的求解方法

3.1 機會約束松弛方法

對于形如式(13)的機會約束優化問題

maxEf0(x,δ)

s.t. Pr(f(x,δ)≤0)≥1-α

(13)

式中：x為決策變量；δ為隨機變量；α為某一特定概率。易知式(14)與式(13)中約束條件等價[18]

p(x):=Pr(f(x,δ)>0)≤α

(14)

設ψ為任一非負、非減的凸函數，并對?z>0，滿足ψ(z)>ψ(0)=1。 則對任意變量Z和任意t>0， 滿足

E[ψ(tZ)]≥E[1[0,+∞](tZ)]=
Pr(tZ≥0)=Pr(Z≥0)

(15)

式中1[0,+∞](·)為指標函數，即(·)≥0取1，否則取0。令Z=f(x,δ)， 并將t轉換為t-1， 得到

p(x)≤E[ψ(t-1f(x,δ))]

(16)

定義Ψ(x,t):=tE[ψ(t-1f(x,δ))]， 則可得

(17)

因此，式(13)可轉換為

(18)

且易知式(18)和式(13)的確定型形式具有相同的凹凸性，因此常用求解確定型優化的方法均可應用于求解式(18)。

當fi(x,δ)=aTx+b，δ=[aT,b]T，ψ(z)=(1+z)2時，式(18)具有更簡潔的解析式，如

(19)

3.2 線性化模型

為便于按式(19)進行松弛，將優化模型進行逐次線性化求解為

(20)

3.3 分區無功備用求解流程

本文對分區無功備用采用逐次優化的過程，首先篩選得到系統的薄弱區域和節點電壓越限區域，對該區域進行無功備用優化，并根據其結果更新系統參數直至獲得滿意解，其流程圖如圖2所示。

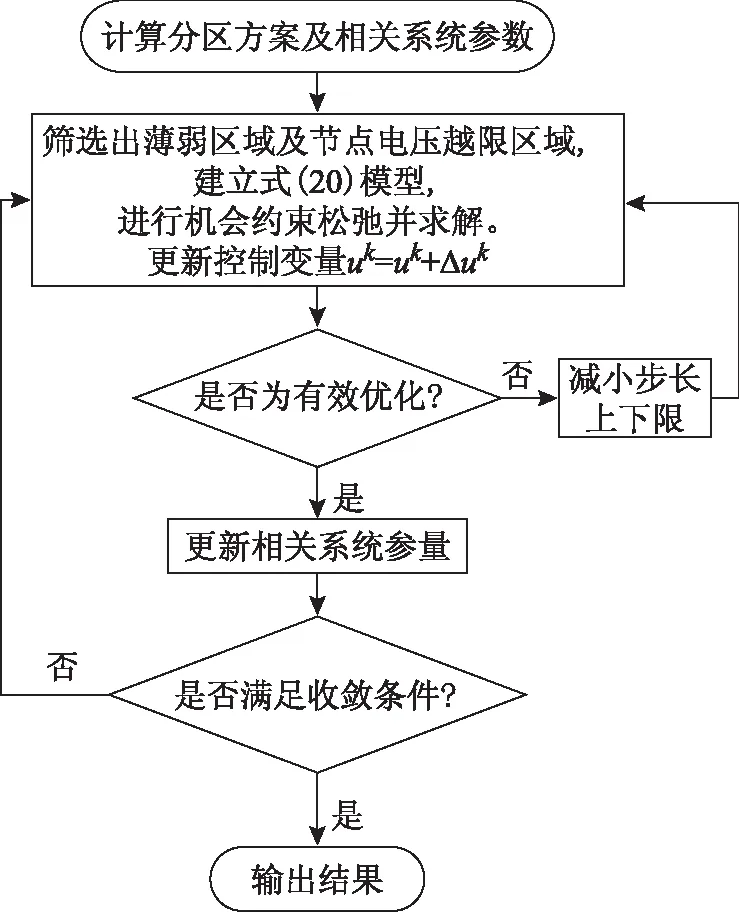
圖2 分區無功備用算法流程Fig.2 Flow chart of the proposed method

薄弱區域定義：

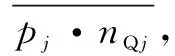
有效優化定義：

算法收斂判據：

1)所有約束條件均滿足。

2)迭代次數達到上限。

4 算例分析

4.1 6節點算例

為說明本文定義的無功備用權系數的有效性，首先采用case6ww系統進行測試，系統接線如圖3所示，節點1為平衡節點，節點2、3為PV節點，其余均為PQ節點，系統詳細參數見Matpower4.1[20]。臨界點處平衡機無功越限，失穩類型為LIB。

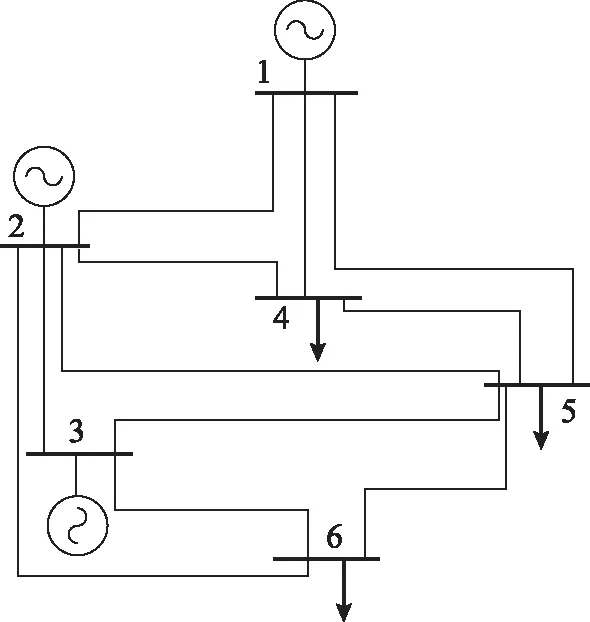
圖3 6節點系統單線圖Fig.3 Diagram of the 6-bus system

根據本文定義，3臺發電機的無功備用權系數分別為0.185 6、0.644 8、0.691 2，說明節點2、3的無功備用價值遠大于節點1。利用策略檢驗無功備用權系數定義的有效性：①方案A：發電機1無功上限提高0.5pu；②方案B：發電機2無功上限提高0.5pu；③方案C：發電機3無功上限提高0.5pu。

在不采用任何措施情況下，case6ww的電壓穩定裕度為0.978 4，而在方案A、B、C調整后，電壓穩定裕度分別為1.036 7、1.124 5、1.151 4。分別增長5.96%、14.93%、17.68%，與無功備用權系數的大小關系吻合較好。

為進一步說明發電機無功備用對電壓穩定裕度的影響，不計發電機無功上限，此時3臺發電機的無功備用系數分別為0.093 7、0.202 8、0.193 8，電壓穩定裕度為2.602 4，在此基礎上實施3種方案。①方案D：節點1端電壓調節至1.1pu；②方案E：節點2端電壓調節至1.1pu；③方案F：節點3端電壓調節至1.1pu。

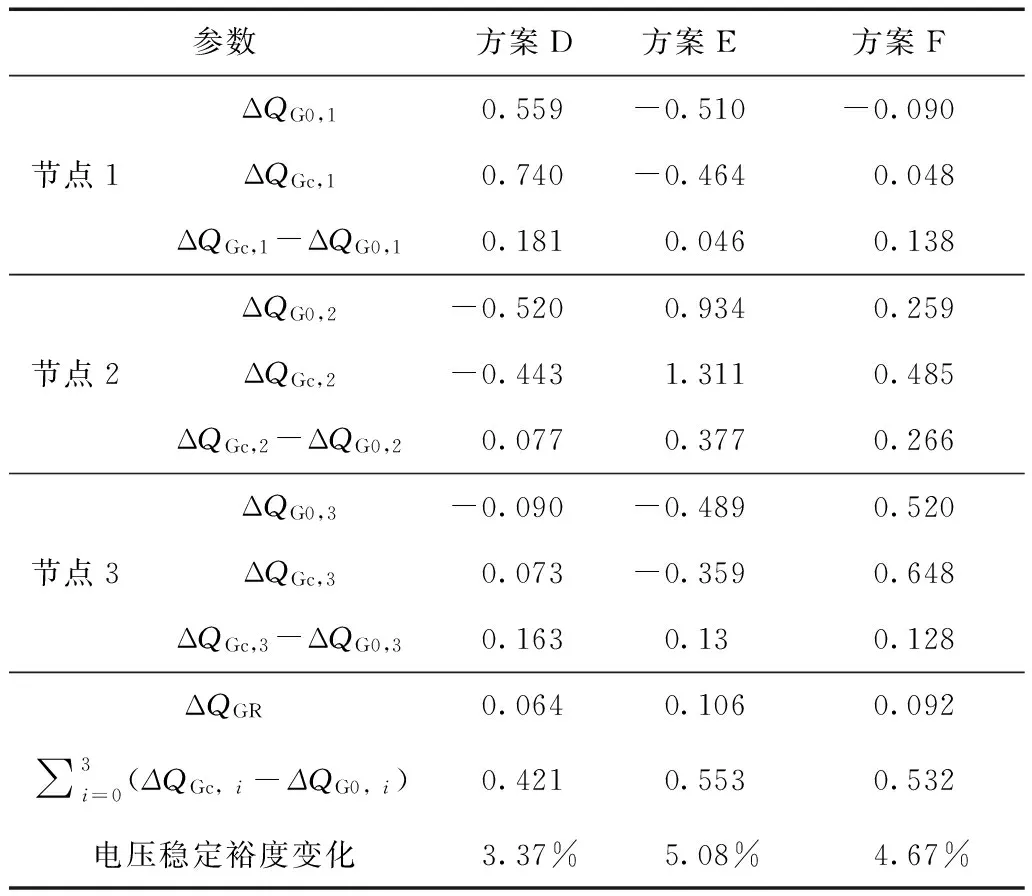
表1 各方案下發電機無功備用變化情況Tab.1 Generator reactive power reserve under different adjustment

從表2中數據可知，方案E、F分別使發電機2、3的無功備用明顯提高，提高了系統總無功備用，電壓穩定裕度上升。從表中也可看出，本文的無功備用定義可準確區分發電機的無功備用價值。

4.2 118節點算例

為說明本文所提隨機無功備用優化方法的有效性，以Matpower 4.1[20]中的IEEE 118節點系統為例，對優化算法進行分析，該系統共有54個發電機節點、9臺變壓器和17個電容補償節點，補償容量上限均為100 Mvar。節點電壓上限均設為1.06，下限為0.96，置信概率p(·)均設為98%。在節點50、51、57、58、93、94、95、96這8個節點裝設200MW的風電場，其中50、51、57、58為同一區域，93、94、95、96為另一區域，區域內風速相關性為0.8，區域間無相關性，風速均滿足威布爾分布W(c,k)=W(10.7, 3.97)。 設負荷均滿足正態分布，期望值等于負荷初始值，標準差為其期望值的5%，相關系數為0.5。

4.2.1 分區無功備用

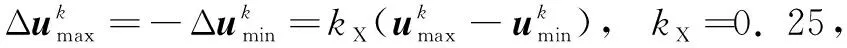
表2 IEEE 118節點系統分區結果Tab.2 Partition scheme of IEEE 118 bus system

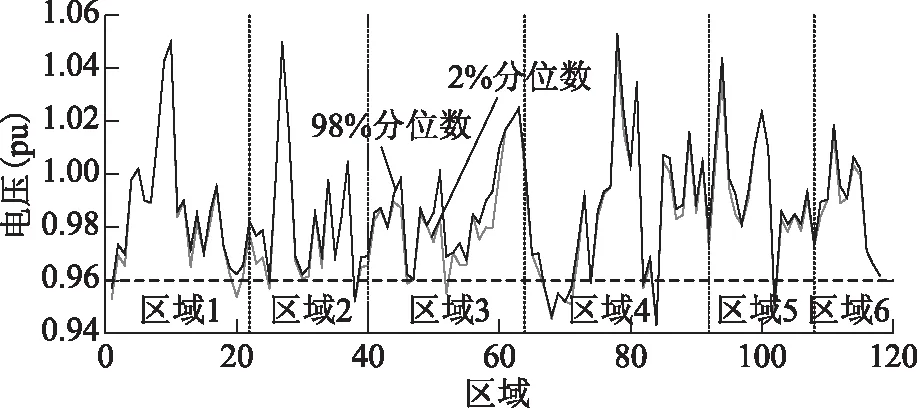
圖4 優化前節點電壓分位數信息Fig.4 Quantile of voltage profile before optimization

算法經過6次迭代收斂，迭代中系統變化情況如表3所示。優化后各區域電壓如圖5所示。

表3 系統狀態變化情況Tab.3 Effect of optimization on system states

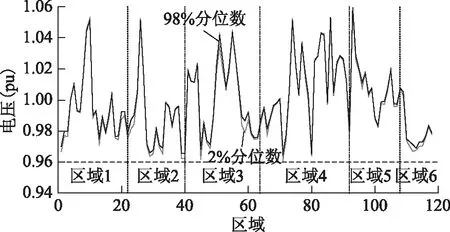
圖5 優化后節點電壓分位數信息Fig.5 Quantile of voltage profile after optimization

從圖5中可看出，本文采用的機會約束凸松弛辦法可有效轉換機會約束，違反的14個機會約束均得到滿足。此外，最薄弱95節點的PV曲線如圖6所示，在嚴重故障方面，支路8-5開斷是嚴重故障，電壓穩定裕度僅0.67，遠低于正常水平。而本文方法得到方案在8-5支路開斷后的負荷裕度由2 821.79 MW上升到3 763.7 MW。

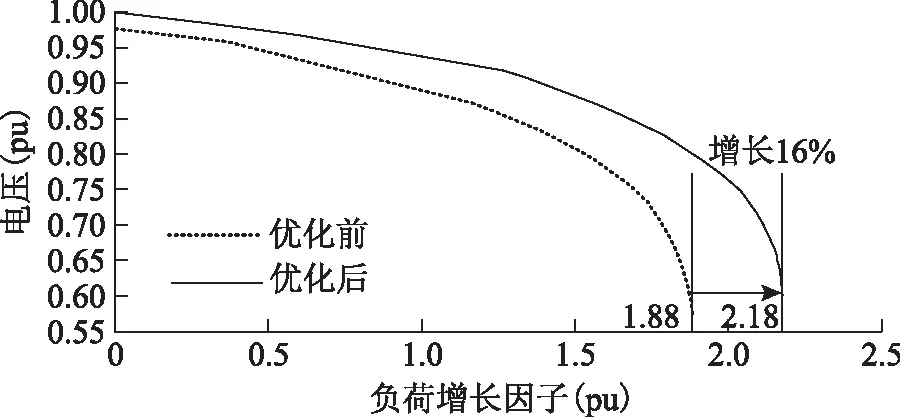
圖6 優化前后PV曲線Fig.6 PV curves before and after optimization

4.2.2 參數對優化結果的影響

為分析參數對優化結果的影響，步長參數kX和分區數與優化得到的電壓穩定裕度之間的關系如圖7所示，與迭代次數關系如圖8所示。

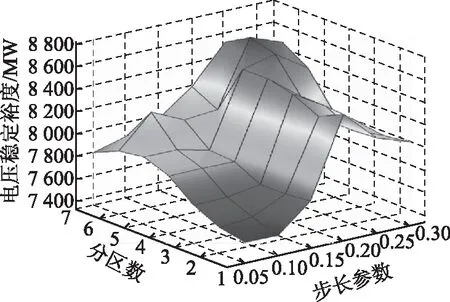
圖7 參數對尋優結果影響Fig.7 Influence of parameter on results of optimization

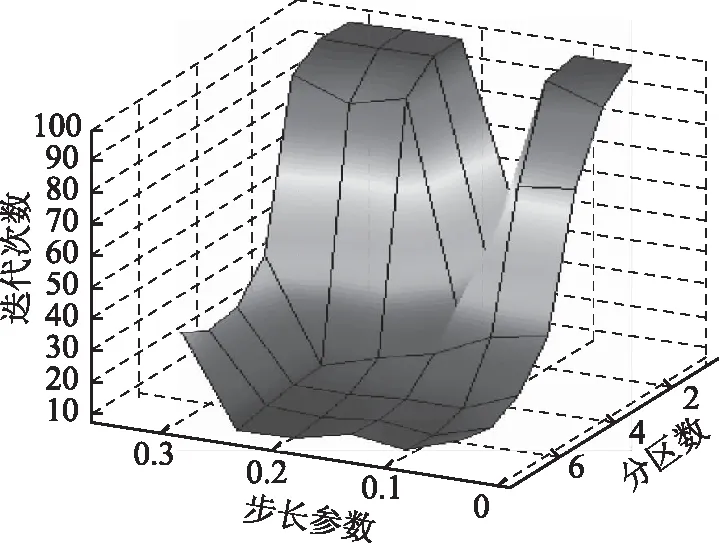
圖8 參數對迭代次數的影響Fig.8 Influence of parameter on iteration times

從圖7和圖8中可看出，步長參數kX和分區數過大和過小都會影響算法的尋優效果，而算法迭代次數受分區數影響更大。當kX較大時，線性化模型的準確度低，可能會因為優化失敗降低解的質量，迭代次數也因此增大；當其過小時則會使迭代次數增多，同樣影響結果。而分區數過小時，會由于少量不合理的控制措施而使優化失敗，系統狀態回滾引發后續的優化失敗，迭代次數急劇增加。

4.2.3 與傳統無功備用優化方法效果對比

隨機無功備用優化是含機會約束的大規模非線性約束規劃問題，通常可采用轉換法[21]、模擬法[22]和點估計法[1]求解。轉換法采用混合蛙跳算法，參數設置同文獻[21]，模擬法和點估計法均將原問題轉換為多次的優化運算，單次計算均采用逐次線性化的優化方法，模擬法采樣規模為200，點估計采用三點法。所得結果對比如表4所示。

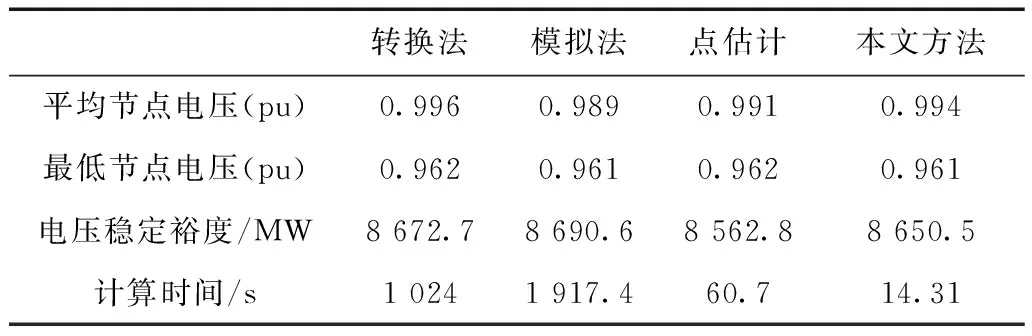
表4 多種方法結果對比Tab.4 Results of different methods for optimization

由表4中數據可知，本文方法求得結果較準確，且計算效率明顯高于其他3種方法，這說明了本文所提機會約束松弛方法的可靠性和有效性。

4.3 實際大系統

為體現本文方法在實際大系統中的效果，本文采用我國某大區域電網2013年夏高方式下網架進行分析，該網絡保留500 kV及以上負荷節點和220 kV及以上發電機節點，風電機裝機容量為3 780 MW。該系統節點數量為1 594，發電機數目為535，線路數量為3 359。電壓上下限分別設為1.05和0.92，其余參數同5.2節，優化前后結果如表5所示。

表5 實際系統優化前后結果Tab.5 Results of real power system before and after optimization

5 結論

本文提出了一種基于機會約束松弛的分區隨機無功備用優化方法。6節點系統證明了本文無功備用定義的有效性，IEEE 118節點系統和某實際系統的仿真結果證明該方法的正確性，松弛方法能有效轉換機會約束，使得優化結果能滿足機會約束而降低系統的運行風險。得到結論如下：

1)本文的無功備用定義能有效識別發電機無功備用的價值。

2)本文采用的機會約束松弛辦法可有效轉換機會約束，使得最終優化結果較好的滿足了機會約束，從而降低系統的運行風險。

3)本文方法能有效改善系統的電壓水平，提高電壓穩定裕度。

4)與多種方法的比較證明本文方法具有較高效率，并能應用于實際電網分析中。

5)本文方法對嚴重故障下的電壓穩定裕度也有一定改善作用。

[1] Fang Sidun，Cheng Haozhong，Song Yue.Stochastic optimal reactive power dispatch method based on point estimation considering load margin[C].Proceedings of 2014 IEEE Power Engineering Society General Meeting，Washington，USA，2014：1-5.

[2] Arya L D，Singh P，Titare L S.Anticipatory reactive power reserve maximization using differential evolution[J].International Journal of Electrical Power & Energy Systems，2012，35(1)：66-73.

[3] Ruiz P A，Sauer P W.Reactive power reserve issues[C].38th North American Power Symposium，Carbondale，USA，2006：439-445.

[4] Menezes T V，da Silva L C P，da Costa V F.Dynamic VAR sources scheduling for improving voltage stability margin[J].IEEE Transactions on Power Systems，2003，18(2)：969-971.

[5] Kataoka Y，Shinoda Y.Voltage stability limit of electric power systems with generator reactive power constraints considered[J].IEEE Transactions on Power Systems，2005，20(2)：951-962.

[6] 劉志文，劉明波，林舜江.REI等值技術在多區域無功優化計算中的應用[J].電工技術學報，2011，26(11)：191-201. Liu Zhiwen，Liu Mingbo，Lin Shunjiang.Research on application of REI equivalent technique into multi-area reactive power optimization computing[J].Transactions of China Electrotechnical Society，2011，26(11)：191-201.

[7] 王綿斌，譚忠富，張麗英，等.市場環境下電網投資風險評估的集對分析方法[J].中國電機工程學報，2010，30(19)：91-99. Wang Mianbin，Tan Zhongfu，Zhang Liying，et al.Power grid investment risk evaluation model based on set-pair analysis theory in power market[J].Proceedings of the CSEE，2010，30(19)：91-99.

[8] Beyer H G，Sendhoff B.Robust optimization-acomprehensive survey[J].Computer Methods in Applied Mechanics and Engineering，2007，196(33-34)：3190-3218.

[9] 張曉花，趙晉泉，陳星鶯.節能減排多目標機組組合問題的模糊建模及優化[J].中國電機工程學報，2010，30(22)：71-76. Zhang Xiaohua，Zhao Jinquan，Chen Xingying.Multi-objective unit commitment fuzzy modeling and optimization for energy-saving and emission reduction[J].Proceedings of the CSEE，2010，30(22)：71-76.

[10]于佳，任建文，周明.基于機會約束規劃的風蓄聯合動態經濟調度[J].電網技術，2013，37(8)：2116-2122. Yu Jia，Ren Jianwen，Zhou Ming.A chance-constrained programming based dynamic economic dispatch of wind farm and pumped-storage power station[J].Power System Technology，2013，37(8)：2116-2122.

[11]馮士剛，艾芊.帶精英策略的快速非支配排序遺傳算法在多目標無功優化中的應用[J].電工技術學報，2007，22(12)：145-151. Feng Shigang，Ai Qian.Application of fast and elitist non-dominated sorting generic algorithm in multi-objective reactive power optimization[J].Transactions of China Electrotechnical Society，2007，22(12)：145-151.

[12]陳杉，陳民鈾，黃薏宸.含分布式發電的配電網多目標無功優化策略研究[J].電力系統保護與控制，2013，41(10)：45-51. Chen Shan，Chen Minyou，Huang Yichen.Multi-objective reactive power optimization of distribution system penetrated with distributed generation[J].Power System Protection and Control，2013，41(10)：45-51.

[13]張聰譽，陳民鈾，羅辭勇，等.基于多目標粒子群算法的電力系統無功優化[J].電力系統保護與控制，2010，38(20)：153-159. Zhang Congyu，Chen Minyou，Luo Ciyong，et al.Power system reactive power optimization based on multi-objective particle swarm algorithm[J].Power System Protection and Control，2010，38(20)：153-159.

[14]王瑞，林飛，游小杰，等.基于遺傳算法的分布式發電系統無功優化控制策略研究[J].電力系統保護與控制，2009，37(2)：24-29. Wang Rui，Lin Fei，You Xiaojie，et al.Research on the reactive power control of distributed generation system based on genetic algorithm[J].Power System Protection and Control，2009，37(2)：24-29.

[15]周任軍，劉志勇，李獻梅，等.采用多隨機變量超分位數方法的機組碳捕集率優化決策[J].電網技術，2014，38(11)：3006-3011. Zhou Renjun，Liu Zhiyong，Li Xianmei，et al.Optimal decision of unit carbon capture rate using multiple random variable superquantile[J].Power System Technology，2014，38(11)：3006-3011.

[16]Newman M E J.Analysis of weighted networks[J].Physical Review E，2004，70(5)：056131.

[17]熊虎崗，程浩忠，孔濤.基于免疫—中心點聚類算法的無功電壓控制分區[J].電力系統自動化，2007，31(2)：22-26. Xiong Hugang，Cheng Haozhong，Kong Tao.Network partitioning for reactive power/voltage control based immune-central point clustering algorithm[J].Automation of Electric Power Systems，2007，31(2)：22-26.

[18]Nemirovski A，Shapiro A.Convex approximations of chance constrained programs[J].SIAM Journal on Optimization，2006，17(4)：969-996.

[19]段玉兵，龔宇雷，譚興國，等.基于蒙特卡羅模擬的微電網隨機潮流計算方法[J].電工技術學報，2011，26(1)：274-278. Duan Yubing，Gong Yulei，Tan Xingguo，et al.Probabilistic power flow calculation in microgrid based on monte-carlo simulation[J].Transactions of China Electrotechnical Society，2011，26(1)：274-278.

[20]PSERC.Power System Engineering Research.Matpower 4.1[EB/OL].http：//www.pserc.cornell.edu/matpower/.

[21]張沈習，陳楷，龍禹，等.基于混合蛙跳算法的分布式風電源規劃[J].電力系統自動化，2013，37(13)：76-83. Zhang Shenxi，Chen Kai，Long Yu，et al.Distributed wind generator planning based on shuffled frog leaping algorithm[J].Automation of Electric Power Systems，2013，37(13)：76-83.

[22]方斯頓，程浩忠，徐國棟，等.基于非參數核密度估計的擴展準蒙特卡洛隨機潮流方法[J].電力系統自動化，2015，39(7)：21-28. Fang Sidun，Cheng Haozhong，Xu Guodong，et al.An extended quasi Monte-Carlo probabilistic load flow method based on non-parametric kernel density estimation[J].Automation of Electric Power Systems，2015，39(7)：21-28.

Stochastic Optimal Reactive Power Reserve Dispatch Based on Convex Relaxation of Chance Constraints Considering Voltage Control Areas

FangSidun1ChengHaozhong1MaZifeng1SongYue2ZhangJian3LiBoqing3

(1.School of Electronic Information and Electrical Engineering Shanghai Jiao Tong University Shanghai 200240 China 2.Department of Electric Engineering of Hong Kong University Hong Kong 3.China Electric Power Research Institute Beijing 100192 China)

In order to address the uncertainties of sustainable energy integration and regional characteristics of reactive power，a stochastic optimal reactive reserve dispatch method based on voltage control area is proposed in this paper.At first，agglomerative clustering and modularity index are employed to find the system reactive area.And then the convex relaxation method is adopted to transform the stochastic optimization model into deterministic.Finally，a successive regional optimal reactive reserve optimization method is proposed.Several test cases demonstrate that convex relaxation is able to convert chance constraints accurately.The proposed method transforms the high dimensional original optimization problem into several regional sub-problems with low dimension，which leads to high computational efficiency.The dispatch scheme has significantly enhanced the reactive power reserve and voltage stability margin.The operational risk of the power system is also decreased，which also enhances the voltage profile ofN-1 scenarios.

Convex relaxation of chance constraints，voltage control area，reactive power reserve，successive regional optimization，voltage stability margin

國家自然科學基金重點項目(51337005)和國家重點基礎研究發展(973)計劃(2014CB23903)資助。

2014-12-29 改稿日期2015-03-09

TM315

方斯頓 男，1991年生，博士研究生，研究方向為電力系統無功與電壓穩定性。(通信作者)

程浩忠 男，1962年生，教授，博士生導師，研究方向為電力系統規劃，電力系統無功與電壓穩定性，電能質量，負荷預測，電力市場。