淺析三角函數問題的解決思路
2015-04-10 13:53:46李素英
新課程(下) 2015年11期
李素英
(江蘇省徐州經貿高等職業學校)
解決三角函數問題時,處理的對象一般是變量的個數、次數的高低和項數的多少等,從這些方面入手,認真審題,周密思考,充分挖掘問題中的隱含條件,就能化繁為簡,順利解決問題.下面筆者就三角函數問題的特點,歸納出三種解決思路,以期拋磚引玉.
思路一:將多個三角函數轉變為一個三角函數
解析:此函數雖略顯復雜,但把ωx看成一個整體后,該函數仍可變形為只含一個三角函數的形式.
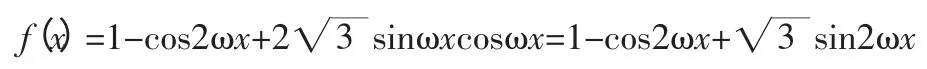
思路二:將三角函數轉變為一元二次函數
(1)y=asin2x+bsinx+c
(2)y=acos2x+bsinx=a(1-2sin2x)+bsinx=-2asin2x+bsinx+a
(3)y=a(sinx+cosx)+bsinxcosx,令t=sinx+cosx,則,,則原函數可化為
例2.求函數f(x)=cos2x-8cosx+7(0≤x≤π)的值域.
解析:此函數形式可變形為一元二次函數的形式.
f(x)=2cos2x-1-8cosx+7=2cos2x-8cosx+6=2(cosx-2)2-2,
∵0≤x≤π,∴-1≤cosx≤1,∴f(x)min=2(1-2)2-2=0,
f(x)max=2(-1-2)2-2=16,即f(x)∈[0,16].
思路三:分式型三角函數的常用處理手段
解析:典型的分式型三角函數,借助正弦函數的取值范圍,能順利解決。
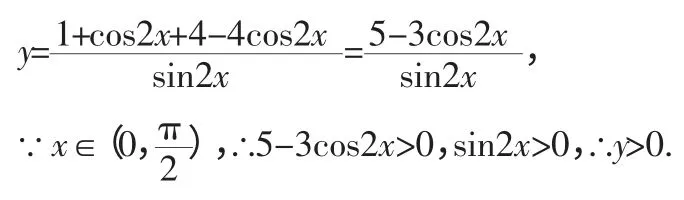
上式可變形為ysin2x+3cos2x=5。其中
猜你喜歡
作文·小學低年級(2025年8期)2025-08-01 00:00:00
中學生數理化·中考版(2023年8期)2023-06-27 06:38:50
小學生學習指導(低年級)(2021年3期)2021-07-21 03:02:36
中華詩詞(2020年1期)2020-09-21 09:24:52
小學生作文(中高年級適用)(2018年5期)2018-06-11 01:22:56
小學生學習指導(低年級)(2018年3期)2018-01-31 02:18:59
數學小靈通·3-4年級(2017年10期)2017-11-08 08:42:59
數學小靈通(1-2年級)(2017年10期)2017-11-08 08:39:18
中學生數理化·七年級數學人教版(2017年11期)2017-04-23 07:18:00
數學大王·中高年級(2016年12期)2016-12-26 21:37:36

