關注三點，生成課堂精彩

江蘇如皋市江安鎮江安小學（226534） 嚴世林

課堂教學是一個充滿生成性的、不確定的、動態發展的過程。在這個過程中，學生會有奇思妙想，也會出現諸多錯誤……教師要時刻關注學生的學習動態，精心預設，合理調控，動態生成，只有這樣，才能使課堂教學更加精彩。

一、關注學習起點，主動應對生成

在學習數學新知之前，學生對所學的新知都會有一些或多或少的學習經驗，這也是學生學習的起點。在數學教學中，教師要時刻關注學生學習的起點，依據學生的理解接受程度，設計出有效的教學策略，起到對教學過程隨時調控的教學目的。

如在教學“時，分，秒”之前，我出示了以下問題：1.鐘面上一共有（ ）個大格；2.每個大格內又分為（ ）個小格；3.鐘面上一共有（ ）個小格。大多數學生看到題目都有種無從下手的感覺，說明了學生對這種表述方式在理解上還存在一定困難。在準確把握學生起點的基礎上，我換了個提問的形式：“你知道這個鐘面上一共有多少個數字嗎？每個數字之間都有一定距離，我們把個距離稱之為一大格，現在，你知道鐘面上有多少個大格嗎？”基于學生理解提出問題，學生很快就能準確給出答案。

在“時，分，秒”的教學中，認識鐘面，了解大格、小格指的是什么，以及分清時針、分針、秒針是教學的基礎。在這個教學過程中，教師通過問題準確把握了學生的起點，然后立足于起點，在基于學生理解認識的基礎上展開。這樣的教學，為課堂教學的動態生成提供了保證。

二、關注學習疑點，充分開發生成

學貴有疑。學生在學習的過程中，只在有疑問時，才會有進一步探索的要求。因此，教師要充分關注學生的學習疑點，巧妙開發利用，進而使學生在存疑、探疑、釋疑的過程中加深對問題的認識，生成精彩的課堂。

如在教學“有余數的除法”時，教學重點是讓學生在擺一擺、分一分中了解余數以及有余數的除法的含義，并且理解除數與余數之間的關系。在教學時，首先以“把7個蘋果平均分給3個學生，每個學生可以分到幾個，還余下幾個”為例，讓學生擺一擺、想一想，學生很容易就得出了“每個學生分2個，還余下1個”的結論。此時，我順勢指出：“余下的這個我們就把它叫做余數。現在你們還有什么疑問嗎？”在教師的鼓勵和支持下，有學生提出自己對除數和余數之間的關系還不是很了解。于是我讓學生分別拿出8根小棒、9根小棒、10根小棒……擺成正方形，并在旁邊寫上算式。

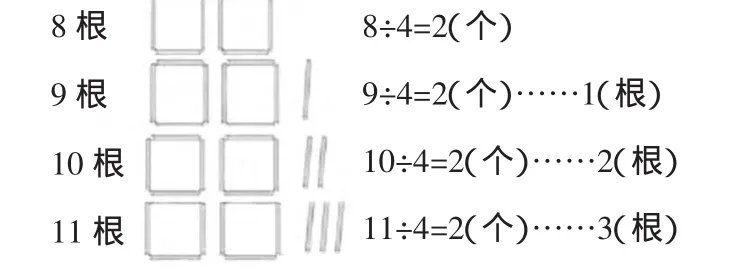
學生經過動手操作得出以上結果后，我再讓學生仔細觀察這些算式中的除數與余數，經過比較，學生輕松得出了“余數一定比除數小”的結論。

在這個教學過程中，面對學生的疑惑，教師沒有直接告知，而是巧妙地開發利用，讓學生通過親自動手實踐來解決這個謎團，使得學生的感受更深刻，提高了學習效率。

三、關注易錯點，有效促進生成

富蘭克林曾說：“垃圾是放錯了地方的寶貝。”在數學教學中，面對教師的提問，學生總會出現各種各樣的錯誤。其實，教師如果利用好這種錯誤，也可以使錯誤資源綻放精彩。因此，教師面對學生的錯誤時，不妨借“錯”發揮。

如教學“利用商不變的規律進行簡便計算”時，我以“8500÷200”為例展開教學，依據被除數和除數同時擴大或者縮小的規律，把原式化為“85÷2”，進而得出了“得數是42，余數是100”的結果。有學生馬上提出了反對意見：“你不是常說余數一定要比除數小嗎？在這里余數怎么比除數大啊？我故作茫然，借題發揮道：“對呀，余數是不可以比除數大的呀，看來這樣的簡算有問題！大家再認真思考一下，確定是不是真的計算錯了？”學生立即認真查找，發現余數100是相對除數是200時的余數，而不是改變后的除數是2的余數，這樣一來，學生豁然開朗。

當學生出現錯誤時，教師借“錯”發揮，引領學生主動探究，發現錯誤的本質。這樣，學生在發現錯誤、追究本質的過程中，收獲了柳暗花明的驚喜，進而把課堂推向了高潮。

總之，在數學教學中，關注學習起點就是關注學生學習的就近發展區；關注學習疑點，就是關注學生探究的起點；關注學習錯點，就是真正的以生為本。就讓我們時刻關注學生，發現問題，主動應對，打造出充滿無限活力的數學課堂吧！