基于圖論模型的一類集成電路布線算法

耿顯亞，許 峰

安徽理工大學 理學院，安徽 淮南 232001

1 引言

集成電路從20世紀60年代開始，到目前為止已經發展到超大規模集成電路。目前我國集成電路的發展非常迅猛，但是和發達國家的水平相比還是有很大的差距。一般來說一個國家電子工業的增長速率是國家經濟增長速率的3倍，而集成電路的增長速率又可以達到電子工業的2倍。這樣估算，再過幾十年我國的集成電路的市場總額將達到世界集成電路市場份額的四分之一。因此，集成電路的發展任重而道遠，只有把集成電路產業發展到世界先進水平，我國的經濟才能在世界處于領先地位。

隨著集成電路技術的飛速發展，除了工藝技術、設備和材料等方面的不斷改進，設計技術的進步也起著舉足輕重的作用。在集成電路設計的每個環節和整體設計中都普遍使用CAD技術，隨著集成度的提高，芯片內部集成的晶體管數目越來越多，集成電路設計的復雜性也越來越高，要在幾十平方毫米的硅片上完成數百萬個器件的電子系統的設計，只靠人工設計是完全不可能的，借助計算機輔助設計工具進行電路設計勢在必行。由于芯片及其之間的關系可以用圖的結構來表示，這樣圖論的思想方法就可以用到超大規模集成電路設計中。組合優化和圖論的方法在超大規模集成電路設計中被廣泛地應用，近幾十年國內外學者已經做了深入的研究，在此領域中出現了許多優秀的成果[1-8]。德國波恩（Bonn）大學離散數學研究所（Research Institute for Discrete Mathematics）一直從事這一領域的研究，該研究所的主要研究人員大多是圖論和組合數學領域的專家，他們自主研發了一套EDA工具（Bonn Tools），被用于上千款IBM芯片的設計。超大規模集成電路設計中許多問題都是NP-難的，在實際應用中常采用啟發式算法。本文主要考慮圖論的思想方法在超大規模集成電路布線中的應用。

2層曼哈頓模型通道布線是一類很普遍并且研究的比較多的布線類型[9-14]。對于2層曼哈頓模型的通道布線問題，有很多比較有效的啟發式算法解決這類問題[15-17]，另外還有很多理論上比較好的改進結果[18-22]。本文主要研究一類2層曼哈頓模型通道布線。

2 通道布線的描述

考慮的是2層曼哈頓模型的通道布線，并且是固定通道的長度。一個通道布線問題是2部的，如果它的線網都包含兩個結點，并且這兩個結點一個在北面的邊界，一個在南面的邊界。一個通道布線問題是稠密的如果北面和南面的兩個邊界上都有屬于線網的結點，就是說沒有空結點（不屬于任何一個線網的結點）。一個線網是平凡的如果該線網只包含兩個結點并且兩個結點在同一列。另外還有兩個與線網有關的圖論概念：水平約束圖HCG和垂直約束圖VCG。

定義1設一個線網Ni，它所占的軌道跨度為Ii，最左邊的結點為li，最右邊的結點為ri，水平約束圖是一個無向圖，Gh=(V，Eh)，其中：

V={Vi|Vi表示Ni在圖中對應的結點}

Eh={(Vi，Vj)|Ii和Ij不能放在一個軌道上}

在一個通道布線問題中，如果一個線網Ni的結點在北面的邊界上，而線網Nj的結點在南面的邊界上，那么就說線網Ni與線網Nj有垂直約束關系。

定義2垂直約束圖是一個有向圖（圖1），Gv=(V，Ev)，其中：

Ev={(Vi，Vj)|Ni和Nj有垂直的約束關系}

圖1 線網的水平約束圖和垂直約束圖

水平約束圖與通道的軌道高度有密切的關系。如果兩個線網有水平約束，那么它們就不能放在同一層軌道上。因此水平約束圖的最大團里面的所有線網都不能放在同一層軌道上，故最大團就是通道布線問題軌道高度的一個下界。

如果兩個線網有垂直約束，那么它們一定就有水平約束，因此垂直約束圖隱含著水平約束圖，反之則沒有這樣的關系。垂直約束圖上的每一條有向路上的線網也具有水平約束，故這些結點都不能放在同一水平軌道上，因此垂直約束圖的最長有向路也是一個通道布線問題軌道高度的一個下界。

3 通道布線的算法

本章考慮的是2部的且垂直約束圖不帶有向圈的布線問題，由前面的定義知道2部的通道布線問題表示每一個線網都只有兩個結點，并且這兩個結點一個在北面的邊界上，另一個在南面的邊界上。現在假定該通道布線的線網垂直約束圖是不含有向圈的。

首先把要考慮的通道布線問題進行公式化的描述。因為垂直約束圖不含有向圈，那么就只包含有向路，假定在垂直約束圖里面有k條有向路，不妨記為：Pn1,Pn2,…，Pnk，這里ni表示路Pni上包含的線網數目。每一個有向路上的線網記為：Ni1,Ni2,…，Nini(i∈{1,2,…，k})。根據這樣的定義，就有下面的式子成立：

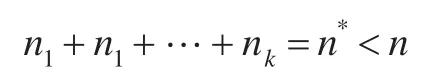
為了介紹算法方便，用一個實例進行說明，這樣可以清晰地顯示算法的進程。在圖2的例子中n=13，n*=10，k=3；并且在圖中，也畫出了該通道布線問題的水平約束圖和垂直約束圖。

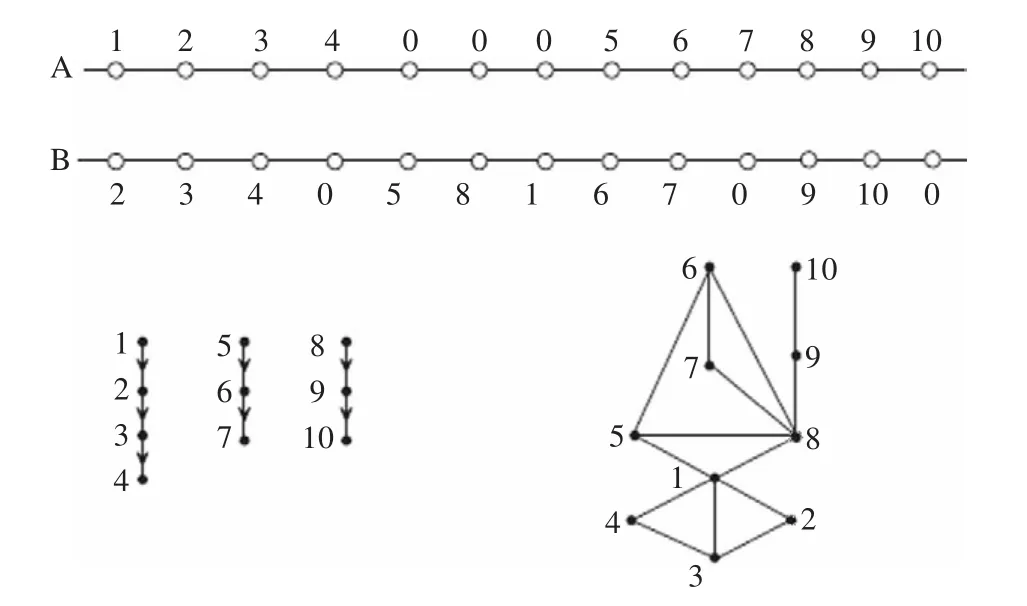
圖2 通道布線的一個實例

下面詳細介紹針對該問題的算法，該算法分為四階段。

第一階段

在進行第一階段之前，首先把平凡的線網先布好，平凡的線網即是它的兩個結點的位置在同一列上，這樣的線網布線時就不用分配水平軌道了，就是說可以直接用一個垂直線段連接起該線網的兩個結點即可。因此可以不用考慮平凡線網，也可以說通道布線問題不包含平凡線網。在后面的算法中，就不再考慮平凡線網的問題。

這里考慮的布線問題的垂直約束圖中只包含有向路，首先，任意的選擇一條有向路，不妨記為Pn1。現在就布選擇出來的該有向路上的線網。按照從北面到南面的順序，給每一個線網分配一個水平的軌道，線網的順序是按照該有向路上的定向來進行，就是說該有向路上的第一個線網分配給它第一個水平軌道，然后依此類推。前面已經定義，本文的通道布線是曼哈頓模型的，就是說一層水平走線，另一層垂直走線，在這里假定上面的一層是垂直走線，而底下的一層是水平走線。根據這個假定，就可以直接布好這個有向路上的線網：對每一個線網，在它所分配到的軌道底層用水平線段處把它的兩個結點連接起來，然后在頂層相應的列用垂直線段把水平線段的端點與結點連接起來。因為前面的定義，該有向路上總共有n1個線網，該有向路就占用了n1行軌道。在圖3中，P101是有向路（1，2，3，4）。

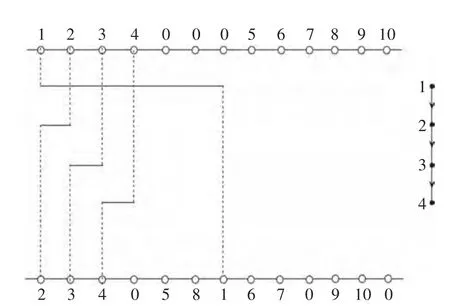
圖3 第一階段的實例演示

第二階段

在第一階段首先處理了一條有向路上的線網，在這個階段再處理一條有向路上的線網。在剩下的有向路中，隨機的選擇一條有向路出來，不妨記該有向路為Pn2。現在布這條有向路上的線網，首先考慮線網N21。

在水平約束圖HCG中，如果線網N21和N11之間沒有邊相連，那么就把線網N21放在N11所在的那個軌道上，也就是第一行軌道上。N21的連接方式與上面的線網的連接方式一樣，就是底層在軌道上用水平線段，頂層用垂直線段把水平線段的端點與結點連接起來。這樣的連接是合理的，因為這兩個線網即沒有水平約束也沒有垂直約束。如果N21和N11在水平約束圖HCG中有邊相連，那么就考慮線網N21和N12，如果這兩個線網在水平約束圖HCG中沒有邊相連，那么就把線網N21放在N12所在的那個軌道上，也就是第二行軌道上，N21的連接方式與上面的線網的連接方式一樣。如果這兩個線網在水平約束圖HCG中有邊相連，那么就繼續考慮下一行上的線網，即是線網N13與N21在水平約束圖HCG上的關系，直到考慮完所有的已經布線的軌道，如果前面已經布線的軌道上面的線網都與N21在水平約束圖HCG上有邊的連接關系，那么就是說前面的軌道都不能夠放置線網N21，只能把線網放在軌道n1+1上，并且這個線網的連接方式與上面的線網是相同的。這樣就把線網N21布好了。

然后再考慮線網N22。如果線網N21是放在軌道n1+1上的，那么就直接可以按照順序把線網N22放在軌道n1+2上。如果線網N21是放在軌道ni(1≤i≤n1)上的，那么首先考慮線網N22和N1i+1，如果它們在水平約束圖HCG中沒有邊相連，那么就把線網N22放在N1i+1所在的那個軌道上，如果它們在水平約束圖HCG中有邊相連，那么考慮線網N22和N1i+2，依此類推，直到找到N22可以放的那個軌道，然后用上面的方法把該線網用水平線段和垂直線段連接起來。對于N2i(2≤i≤n2)，用上面處理線網N22的方法，可以找到一個合適的軌道把該線網布好。圖4是這個階段的一個實例演示。

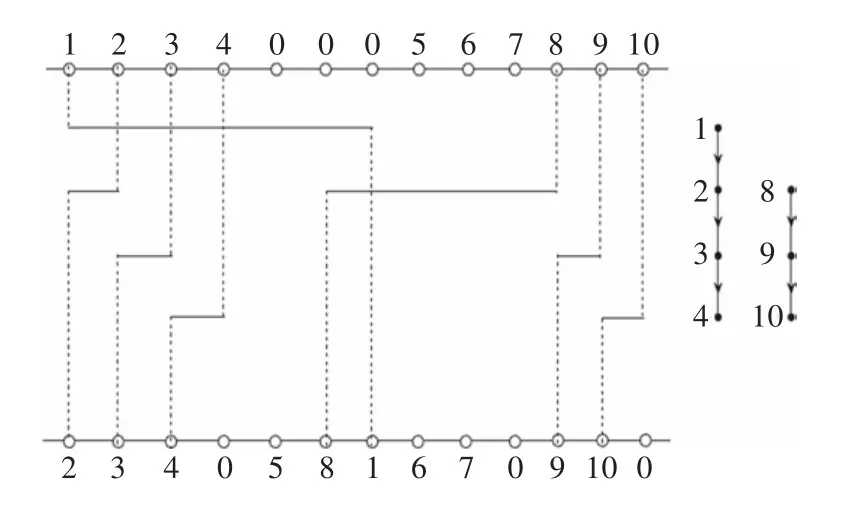
圖4 第二階段的實例演示

第三階段

在前面兩個階段首先處理了兩條有向路上的線網，在這個階段再處理一條有向路上的線網。在剩下的有向路中，隨機的選擇一條有向路出來，不妨記該有向路為Pn3。現在來布這條有向路上的線網，首先考慮線網N31：策略是找到該線網所能放置的最靠近北面的軌道，因此就從第一行軌道開始考慮。目前在第一行軌道上，有可能有兩個線網N11和N21布在該軌道上，至少也有一個線網N11布在該軌道上，N21是否能放置在該軌道是不確定的。所以確定線網N31是否能布在該軌道上，就要在水平約束圖上看線網N31與軌道上面的線網之間的關系。如果線網N31和第一行軌道上的線網之間沒有邊相連，那么就把線網N31放在該軌道上，也就是第一行軌道上。N31的連接方式與上面的線網的連接方式一樣，就是底層用水平線段在軌道上，頂層用垂直線段把水平線段的端點與結點連接起來。這樣的連接是合理的，因為這個線網與第一行軌道上面的線網即沒有水平約束也沒有垂直約束。

如果線網N31至少與第一行軌道上的一個線網之間在水平約束圖HCG中有邊相連，那么就考慮線網N31和第二行軌道上面的線網，這行軌道上的線網也是不確定的，該軌道上至少有一個線網N12，另外還可能有線網N21和N22，具體是否有這些線網要看前面的階段的情況。現在如果N31與第二行軌道上的所有線網之間在水平約束圖HCG中都沒有邊相連，那么就把線網N31放在該軌道上，也就是第二行軌道上，N31的連接方式與上面的線網的連接方式一樣。如果線網N31至少與第二行軌道上的一個線網之間在水平約束圖HCG中有邊相連，那么就繼續朝下面的軌道進行掃描，類似上面的方法，直到找到合適的軌道來布線線網N31。

然后再考慮線網N32。如果線網N31是放在最下面的那個軌道上，就是說這個軌道下面的軌道都沒被占用，那么就直接可以按照順序把線網N31放在下一軌道上。如果線網N31是放在軌道ni上，并且該軌道ni下面還有已經用過的軌道，那么首先考慮線網N22和軌道ni+1上的線網，如果它們在水平約束圖HCG中沒有邊相連，那么我們就把線網N32放在軌道ni+1上，如果它們在水平約束圖HCG中有邊相連，那么考慮線網N22和軌道ni+1上的線網，依此類推，直到找到N32可以放的那個軌道，然后用上面的方法把該線網用水平線段和垂直線段連接起來。

對于N3i(3≤i≤n3)，用上面處理線網N32的方法，可以找到一個合適的軌道把該線網布好。圖5是這個階段的一個實例演示。

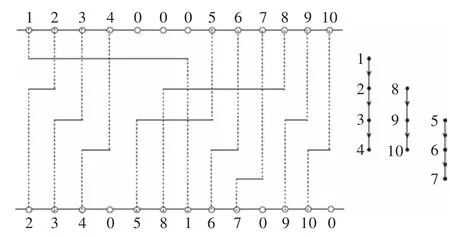
圖5 第三階段的實例演示

第四階段

前面的三階段已經處理了三條有向路上的線網，如果這時候有向路還沒處理完，那么剩下的有向路Pn4，Pn5，…，Pnk就按照階段三的方法，就可以把這些線網全部都布線好。這樣本文的算法就完成了，下面分析下這個算法的時間復雜性及對比其他的算法所具有的優勢。

現在來分析算法的復雜性。

當在第一階段選擇了一條有向路，需要固定的時間來布這條有向路上面的線網；當在第二階段選擇了一條有向路，需要進行n1次比較；當在第三階段選擇了一條有向路，至多需要進行n1+n2次比較。依此類推，當選擇了第k條有向路，至多需要進行n1+n2+…+nk次比較。

這樣如果這個算法完成，至多需要比較的次數C為：

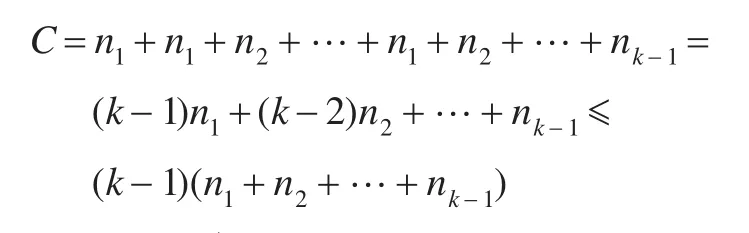
因為n＞n*=n1+n2+…+nk-1+nk，所以有k＜n。這樣由上面的式子就可以得到：

C＜n·n+n2

因為每次的比較需要固定的時間，所以這個算法能在多項式時間內完成。

現在分析本文的算法所得到的軌道上界及與其他算法的比較。

文獻[22]給出了該問題的一個算法，該算法對每一個線網分配一行軌道，故總共需要n*行軌道來進行布線。在該算法中，考慮線網之間的水平約束，讓盡可能多的線網放在同一行軌道上，布線需要的軌道高度小于或等于n*。下面來進行詳細的分析：

情況1如果最長路為Pm，并且把這個最長路首先選擇出來，就是說先用前面的nm軌道來進行布線。再選擇其他的有向路時，如果都是可以放在前面的nm行軌道中來進行布線，那么算法完成時，就總共需要nm行軌道來進行布線。所以在這種情況下，算法得到的軌道高度為nm，再加上nm＜n*，就可以得到在這種情況下本文算法是更優的。

情況2如果在算法的第二到第四階段，后面的有向路上的線網都不能用前面已經用過的軌道，就是說每次處理一個線網時，它都會和前面每一行上面的線網在水平約束圖上有邊相連，只能用一個新的行來進行布線。那么這種情況下，本文算法就同樣是每一個線網分配到一個軌道，這樣算法完成時候所用到的軌道高度為n*，本文算法就和前面的算法得到的結果是一樣的。

情況3如果算法的第二到第四階段，有些線網可以用前面已經用到的軌道，但是并不是所有的線網都可以用到前面的軌道，這種情況就是介于第一種情況和第二種情況之間，這時本文算法完成時所用到的軌道高度是大于最長路上的點數而小于所有的線網之和。在這種情況下，本文算法同樣是優于前面的算法。

由前面的三種情況可知，本文算法能夠得到更優的布線軌道高度。

4 結束語

針對一類2層曼哈頓模型的通道布線問題給出有效算法。通道布線問題的線網約束關系可用水平約束圖（無向）HCG和垂直約束圖（有向）VCG來表示。針對2部且垂直約束圖不包含有向圈的布線問題，提出了一個依據圖論模型的最優軌道高度布線算法。該算法根據通道上結點的水平約束圖和垂直約束圖，依次安排好每一個結點的布線軌道，進而通過通孔可以把所有的結點在2層軌道上布線完成。計算分析結果表明，相比較于目前的算法，本文算法可以得到更好的軌道高度。

[1]洪先龍，嚴曉浪，喬長閣.超大規模集成電路布圖理論與算法[M].北京：科學出版社，1998：2-15.

[2]Lee C Y.An algorithm for path connections and its applications[J].IRE Trans on Electronic Computers，1961：346-365.[3]Soukup J.Fast maze router[C]//Proc of 15th Design Automation Conference，1978：100-102.

[4]Hadlock.A shortest path algorithm for grid graphs[J].Networks，1977，7：323-334.

[5]Hightower D W.A solution to the line routing problem on the continuous plane[C]//Proc of the 6th Design Automation Workshop，1969：1-24.

[6]Mikami K，Tabuchi K.A computer program for optimal routing of printed circuit connectors[J].IFIPS Proc，1968，47：1475-1478.

[7]Chiang C，Sarrafzadeh M，Wong C K.A weighted steinertree-based global router[C]//Proceedings of International Conference on CAD，1992.

[8]Heisterman J，Lengauer T.The efficient solution of integer programsfor hierarchical global routing[J].IEEE Trans on CAD，1991，10：748-753.

[9]Caeden R C，Cheng C K.A global router using an efficient approximate multicommodity multiterminal flow algorithm[C]//Proc of IEEE/ACM Design Automation Conference，1991：316-321.

[10]康志偉.一種新的基于關鍵路徑的時延驅動總體布線算法的研究及其實現[D].北京：清華大學，1995.

[11]Huang J，Hong X L，Cheng C K，et al.An timing-driven global routing algorithm[C]//Proc of IEEE/ACM Design Automation Conference，1993：596-599.

[12]Hong X L，Xue T X，Huang J，et al.An efficient timing driven global routing algorithm for gate array and standard cell design[J].IEEE Trans on CAD，1997，16：1323-1331.

[13]Parng T M，Tsay R S.An new approach tosea-of-gates global routing[C]//Proc of International Conference on CAD，1989.

[14]崔穎惟，喬長閣，洪先龍，等.一種基于擁擠度分析的層次迭代PCB總體布線算法[J].微電子和計算機，1995（S）：58-60.

[15]Recski A，Salamon G，Szeszleer D.Improving size bounds for subcases of square-shaped switchbox routing[J].Periodica Polytechnica：Ser EL ENG k，2004，48：55-60.

[16]Yan J T，Chen Z W.Obstacle-aware length-matching bus routing[C]//Proc of the 2011 International Symposium on Physical Design，2011：61-67.

[17]Golda B，Laczay B，Mann Z A，et al.Implementation of VLSI routing algorithms[C]//Proc of IEEE 6th Internat Conf on Intelligent Engineering Systems，Croatia，2002：383-388.

[18]Kohira Y，Suehiro S，Takahashi A.A fast longer path algorithm for routing grid with obstacles using biconnectivity based length upper bound[C]//Proceedings of Asia and South Pacific Design Automation Conference，2009：600-605.

[19]Bui T N，Chauduri S，Leighton F T，et al.Graph bisection algorithms with good average case behaviour[J].Combinatorica，1987，7：171-191.

[20]Garey M R，Johnson D S.Computers and intractability：a guide to the theory of NP-completeness[M].San Francisco，CA：W H Freeman and Co，1979.

[21]Kramer M R，van Leeuwen J.The complexity of wire routing and finding minimum area layouts for arbitrary VLSIcircuits[M]//Advancesin Computing Research，Volume 2：VLSI-Theory.Greenwich，Connecticut：JAI Press，1984：129-146.

[22]SzeszleerD.A new algorithm for2-layer，manhattan channel routing[C]//Proc of the 3rd Hungarian-Japanese Symposium on Discrete Mathematics and Its Applications，2003：179-185.