不完備決策系統規則獲取的相容矩陣算法

汪 凌

安慶師范學院 經濟與管理學院，安徽 安慶 246011

1 引言

決策規則獲取是粗糙集理論及應用研究的一個重要內容。基于粗糙集的決策規則獲取本質上是按照屬性特征將對象進行分類的問題。目前已有很多文獻研究了不完備信息系統的決策規則獲取方法。如文獻[1-3]給出了基于決策矩陣的增量式規則獲取算法，該算法需要計算和保存分辨矩陣的中間環節，時間復雜度較高；文獻[4-5]提出了利用上下近似集來填補空缺值并提取決策規則的算法，該算法適用于系統中空值較少的情況；文獻[6]提出了基于量化容差關系的規則獲取算法，該算法較多地依賴于先驗知識；文獻[7]給出基于相容關系的不完備信息決策系統規則提取算法，文獻[8-9]給出了基于廣義決策函數及擴展形式的決策規則獲取算法等。但這兩種方法都存在一定的局限性，如計算相容矩陣或分配矩陣計算復雜，占用空間大，以及數據集很大時的規則獲取效果不理想等[10-11]。針對以上問題，本文根據不完備信息決策系統中相容條件屬性矩陣和決策屬性矩陣的概念，通過計算分析矩陣，提出一種基于相容矩陣的不完備信息決策系統規則獲取算法，并從理論上對算法進行分析。通過實例驗證了該算法的正確性和有效性。

2 算法理論基礎

2.1 不完備信息系統與廣義決策函數

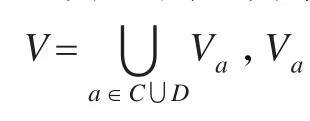
定義2不完備信息決策系統DS=＜U，C∪D，V，f＞，???B?C，U上的一個相容關系定義為：

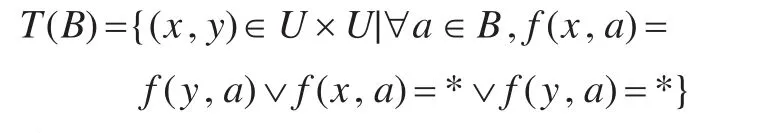
令TB(x)={y∈U|(x，y)∈T(B)}，對于屬性子集B而言，TB(x)是與x可能不可分辨的對象的最大集合。

定義3不完備信息決策系統DS=＜U，C∪D，V，f＞，U={x1，x2，…，xn}，B?C，廣義決策函數 ?B:U→P(Vd)定義為：

?B(x)={i|i=f(y，d)，y∈TB(x)}

其中，P(Vd)表示Vd的冪集，?B(x)表示TB(x)中元素在d上取值集合。

性質1不完備信息決策系統DS=＜U，C∪D，V，f＞，對?x∈U，若Card(?C(x))=1，則稱DS是協調（或相容、一致）的，否則稱DS是不協調（或不相容、不一致）的。

性質2[13-14]不完備信息決策系統DS=＜U,C∪D,V,f＞，設X為具有性質∧(c，v)(c∈C，v∈Vc)的實例集合，Y為具有性質∨(d，w)(w∈Vd)的實例集合，則：

（1）決策規則γ:∧(c，v)→∨(d，w)為真當且僅當X?Y，其中C為規則條件部分的所有屬性集合。

（2）決策規則γ:∧(c,v)→∨(d,w)(c∈C,v∈Vc,w∈Vd)是最優的當且僅當該規則為真且出現在γ中的合取與析取的真子集構成的任何規則均為假。

由上述定義及性質定理可知，對于任意x(x∈U)，最優規則的決策部分為 (d，w1)∨(d，w2)∨…∨(d，wn)，則有{w1，w2，…，wn}=?C(x)。

2.2 條件屬性矩陣和決策屬性矩陣

定義4[15]不完備信息決策系統DS=＜U,C∪D,V,f＞，U={x1，x2，…，xn}，則屬性子集B?C對應的相容條件屬性矩陣MB定義為：

其中，mij為相容條件屬性矩陣中第i行j列的元素，i，j=1，2，…，n。

定義5[15]不完備信息決策系統DS=＜U,C∪D,V，f＞，U={x1，x2，…，xn}，DS的決策屬性矩陣 MD定義為：

其中，mij為決策屬性矩陣中第i行j列的元素，i，j=1，2，…，n。顯然，決策屬性矩陣是一主對角線為1的n階對稱矩陣。

條件屬性子集相容矩陣表述的是該條件屬性子集所確定的不完備信息決策系統中所有實例的相容關系；而決策屬性矩陣表達的則是所有實例間確定不同決策屬性值的區分關系。

在?C、MB及 MD等定義描述的基礎上，可以得出定理1。

定理1不完備信息決策系統DS=＜U，C∪D，V，f＞，U={x1，x2，…，xn}，屬性子集B?C對應的相容條件屬性矩陣，決策屬性矩陣 MD=，其中、、(1≤i≤n)是 1×n維向量，上標T表示矩陣的轉置。若存在的第i行與的第i行相互一致，則存在一條決策規則：

證明根據條件屬性矩陣與決策屬性矩陣的定義，如果的第i行與的第i行相互一致，意味著對于條件屬性子集B，對象xi與決策不可分辨類D中的任意對象xj之間都是不相容的。反之，如果在決策屬性類別中存在yk與xi相容，則有yk∈TB(xi)，所以會存在不一致現象，與相互一致矛盾。因此，對于?xj∈TB(xi)，f(xj，d)∈?C(xi)，必然存在一條決策規則：。

定理1表明，當條件屬性子集確定的一個實例的廣義決策函數值與整個條件屬性集確定的廣義決策函數值相互一致時，必然能得到一條決策規則，這實際上給出了從不完備信息決策系統中提取相應決策規則集的方法。

3 不完備決策系統規則獲取的相容矩陣算法

3.1 算法思想及描述

根據以上命題和定理，提出一種相容關系下基于矩陣計算的不完備決策系統規則獲取算法。該算法通過計算相容屬性矩陣和決策屬性矩陣，當條件屬性子集確定的一個實例的廣義決策函數值與整個條件屬性集確定的廣義決策函數值相互一致時，就可直接生成一條決策規則。采用相同的分析處理方法，就可從不完備信息決策系統中提取出全部的決策規則集。不完備信息決策系統中大數據集的決策規則獲取流程，如圖1所示。

不完備信息決策系統規則獲取的相容矩陣算法具體過程描述如下所示。

輸入：不完備信息決策系統DS=＜U，C∪D，V，f＞，U={x1，x2，…，xn}，C為條件屬性集，D為決策屬性集。

輸出：DS=＜U，C∪D，V，f＞的所有決策規則集。

步驟1計算DS中條件屬性C對應的相容條件屬性矩陣MC和決策屬性矩陣MD。

步驟3 fori=1ton。

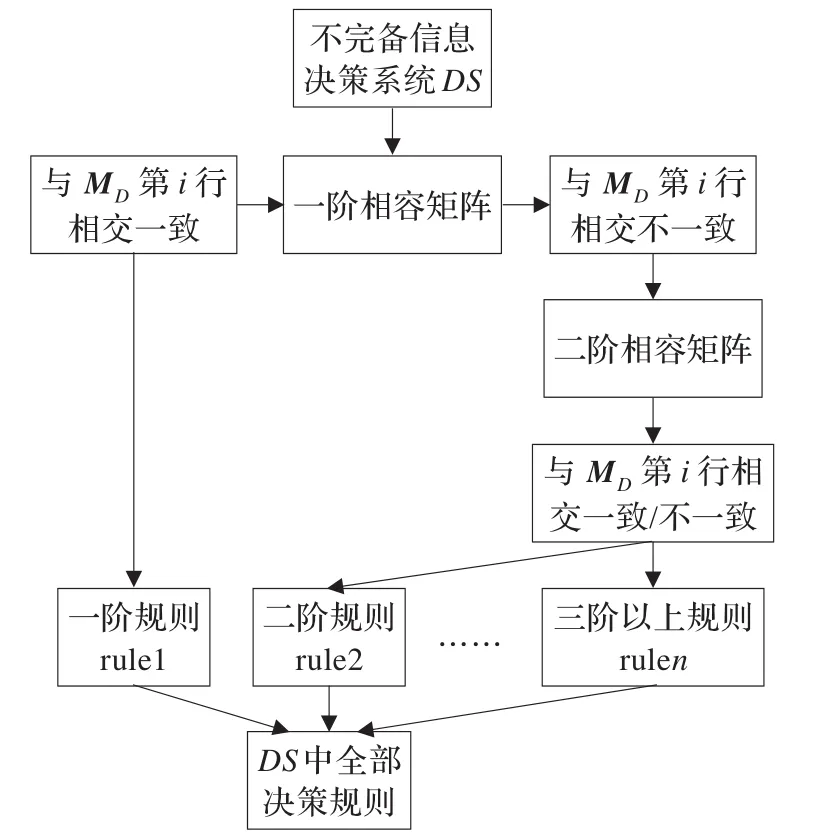
圖1 不完備信息決策系統大數據集的規則獲取流程

（1）取一階相容條件矩陣M{c}的第i行與決策屬性矩陣MD的第i行相交；

（2）若存在 M{c}的第i行與 MD的第i行不一致，nexti，否則轉步驟4。

步驟4根據對象xi的屬性第i行對應的屬性cm∈C，dn∈D的取值生成決策規則：∧(cm=vcm)→∧(dn=vdn)，同時將第i行置為零，提取出所有的一階決策規則。

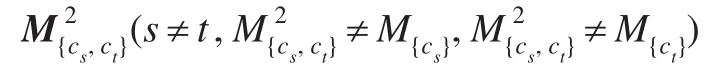
步驟6采用類似步驟5的處理方法提取所有三階以上的決策規則，直至無非零的同階相容矩陣為止，最后輸出所有的決策規則集。

3.2 算法分析

上述規則獲取算法中的相容條件屬性矩陣和決策矩陣的生成是執行整個算法的基礎。因此，本算法的計算復雜度主要由步驟1～步驟5決定。

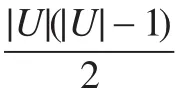
綜合以上分析可知，本算法總的計算復雜度為O(|U|22|C|)，計算量的增長相對于對象個數是多項式級的，相對于屬性個數是成指數級形式的。

本算法在數據計算量上具有較大的優勢，矩陣運算將粗糙集規則提取過程中的復雜比較過程轉換成對簡單的0、1矩陣或向量的操作，而不是對象集的處理。此外，由于決策屬性矩陣只考慮上三角或下三角即可獲取相同結果，因而本算法能夠減少一半的矩陣計算量，大大提高了算法的效率。

4 實例分析

為了驗證算法的有效性，以某城市交通流狀態不完備信息決策系統為例計算最小決策規則集。該不完備信息決策系統如表1所示，其中論域U={x1，x2，…，x6}，條件屬性集C={F，S，D，L}，其中F表示Traffic Flow，S表示 Average Speed，D表示 Vehicle Density，L表示Team Length，決策屬性g0gggggg表示Mode。

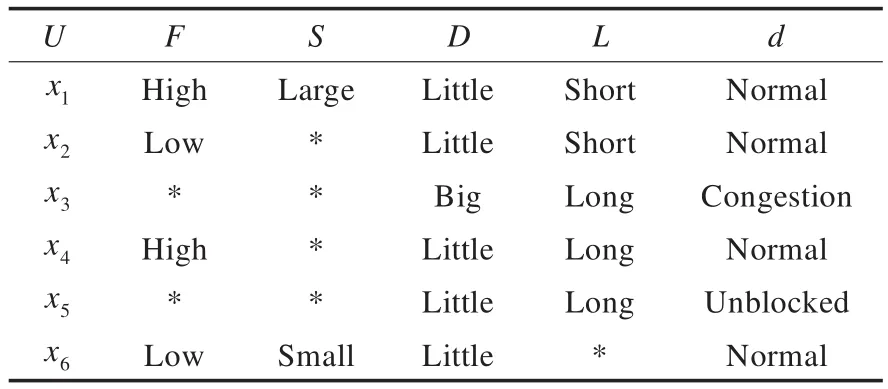
表1 城市交通交通流狀態不完備信息決策表

表1所示的不完備信息決策表中，存在多個條件屬性值未知，因此可以根據上述算法步驟對表1進行如下處理：

（1）根據步驟1，計算不完備信息決策表DS的決策屬性矩陣MD和條件屬性矩陣MC：

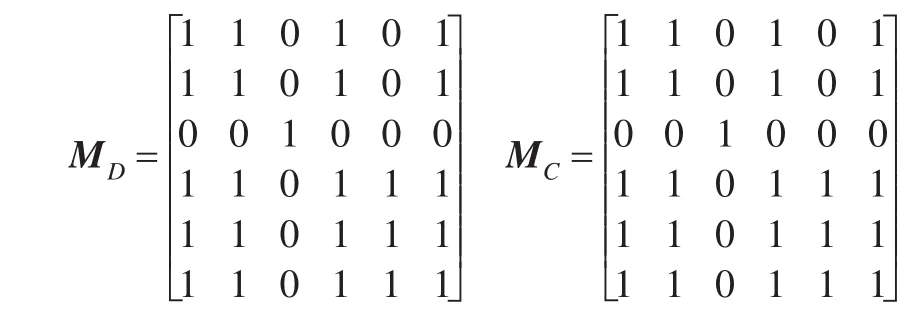
（2）根據步驟2，計算一階相容條件屬性矩陣：

（4）根據算法步驟5，將（3）中所有非零一階相容條件屬性矩陣兩兩相交，得到如下三個滿足條件的所有二階相容屬性矩陣：

對提取的決策規則進行刪除、合并等步驟操作，得該不完備信息決策表最終的決策規則集如表2所示。

表2 城市交通流狀態決策規則集

決策規則對應的語言描述分別為：

rule1如果該路段或交叉口車輛密度是大，則交通流狀態為擁擠的；

rule2如果該路段或交叉口車輛密度是小，則交通流狀態為正常的或暢通的；

rule3如果該路段或交叉口車隊長度是短，則交通流狀態為正常的。

通過提取以上決策規則，即可對城市交通流狀態模式進行辨識。將所有決策規則存儲于城市交通管理決策支持系統中，則可直接判別出任一時刻的交通流狀態模式。

將相同的數據集采用Rosetta Version1.4.41進行規則提取，通過分析比較發現，兩種算法得到的決策規則數基本一致，且該矩陣算法減少了計算量，具有較高的運算效率，實例分析表明了該算法的有效性和實用性。

5 結論

決策規則獲取是粗糙集理論及應用研究的一個重要內容。現有的決策規則獲取算法的低效性一定程度上限制了粗糙集理論的廣泛應用，因而尋求高效的規則獲取算法具有重要意義。本文基于相容關系下的條件矩陣和決策矩陣，提出一種基于相容矩陣運算的不完備決策系統規則獲取算法。該算法在提取規則時減少了矩陣生成的比較次數，降低了矩陣占用空間，通過比較向量大小即可快速求出大數據集的全部決策規則集，因而大大提高了規則獲取效率，對于基于規則獲取的系統辨識而言具有較強的實用價值。

[1]Liu Yong，Xu Congfu，Li Xuelan，et al.A dynamic incremental rule extracting algorithm based on the improved discernibility matrix[C]//Proceedings of the IEEE International Conference on Information Reuse and Integration.NV，USA.2003.NJ，USA：IEEE Computer Society Press，2003：93-97.

[2]李春生，尹旭日，陳世福.基于Rough集的規則學習研究[J].小型微型計算機系統，2001，22（8）：982-984.

[3]Kryszkiewicz M.Rules in incomplete information system[J].Information Science，1999，113：271-292.

[4]Leung Y，Wu W.Knowledge acquisition in incomplete information system：a rough set approach[J].European Journal of Operational Research，2006，168：164-180.

[5]Hong Tzungpei，Tseng Lihui，Wang Shyueliang.Learning rules from incomplete training examples by rough sets[J].Expect Systems with Applications，2002，22（4）：258-293.

[6]Stefanowski J，Tsoukias A.Valued tolerance and decision rules[M]//Ziarko W，Yao Y.Rough Sets and Current Trends in Computing.Berlin：Springer，2002：271-278.

[7]Ziarko W.Variable precision rough set model[J].Journal of Computer and System Sciences，1993，46（1）：39-59.

[8]黃兵，周獻中.不完備信息系統分配約簡與規則提取的矩陣算法[J].計算機工程，2005，31（17）：20-22.

[9]Mollestad T，Skowron A.A rough set framework for data mining of propositional defalut rules[C]//Proc of the 9th International Symposium on Methodologies of Intelligent Systems，1996：448-457.

[10]尹旭日，陳世福.一種基于Rough集的缺損規則挖掘算法[J].計算機研究與發展，2000，12（37）：1441-1445.

[11]Komorowski J.ROSETTA：a rough set toolkit for analysis of data[C]//Proc of the 3rd International Joint Conference on Infromation Sciences.SanJose，Calfornia，USA，1997.North Calfornia，USA：Durham，1997，3：403-407.

[12]Wu Weizhi，Mi Jusheng，Zhang Wenxiu.A new rough set approach to knowledge discovery in incomplete information systems[C]//IEEE Proc of the 2nd International Conference on Machine Learning and Cybernetics，2003：1713-1718.

[13]Pawlak Z.Drawing conclusions from data-the rough set way[J].International Journal of Intelligent Systems，2001，16：3-11.

[14]Hu X H.Knowledge discovery in database：an attributeoriented rough setapproach[D].Regina：University of Regina，1995.

[15]Ziarko W，Hu N.Rule discovery from databases with decision matrices[C]//Proc of the International Conference on Methodologies for Intelligent System（ISMIS96），Zakopane，Poland，1996.Heidelberg，Germany：Springer-Verlag，1996：653-662.