Boole環上的粗糙近似算子
李興寬
云南民族大學 管理學院,昆明 650031
粗糙集理論是一種新的處理不確定性問題的數學工具[1-2]。自1982年由波蘭數學家Pawlak首次提出以來,經過二十多年的研究與發展,已經在理論和實際應用上取得了長足的發展,特別是由于20世紀80年代末和90年代初在知識發現等領域的成功應用而受到了國際上廣泛關注。目前,它已經在人工智能的諸多領域中得到了成功的應用。
隨著粗糙集理論的成功應用,關于其數學基礎的研究工作也逐漸受到學術界關注。不同背景下的粗糙近似是粗糙集理論的一個研究熱點。Iwinski[3]討論了粗糙集的格論性質;Pomy與Pomykala[4]證明了某一論域上的粗糙集形成一個雙Stone代數;Yao與Lin[5-6]證明了基于自反和傳遞關系的粗糙集代數是模態邏輯系統S4的恰當的模型;張化光、梁洪力研究了基于 Boole代數[7]的粗糙近似;陳建飛、林公源研究了基于Griss代數的粗糙近似[8];陳世聯研究了基于蘊含格[9]的粗近似;趙濤、秦克云研究了基于分子格等的粗糙近似[10];同時,還有一些學者研究了半群、群、環背景下的粗糙近似算子[11-13],這些粗糙近似豐富和發展了粗糙集理論。
目前對以Boole環為基礎的粗糙集理的研究卻非常少見,本文以Boole環為基礎,定義了Boole環上的粗糙上近似和下近似,研究了Boole環上的粗糙近似算子及其性質,進一步豐富和發展了粗糙集理論。
1 Boole環及其上的同余關系
定義1[14]設(S,*,+)是一個環,若?a∈S,有a*a=a,則稱S為Boole環。
性質1[12]若S為Boole環,則 ?a∈S,有a+a=0,且S是可換環。
定義2[15]設(S,*,+)是一個環,R是S上的一個等價關系,若 ?a,b,c,d∈S,有aRb,cRd?(a+c)R(a+d),(ac)R(bd),則稱R是S上的一個同余關系。
由此,R是環(S,*,+)上的同余,就是指R既是群(S,+)上的同余,又是半群(S,*)上的同余。
定義3 設 (S,*,+)是一個Boole環,?x,y∈S,規定S上的二元關系:

易知,≤1,≤2是S的偏序關系。
設(S,*,+)是一個Boole環,R是S上的一個同余關系。則S/R={[x]R|x∈S}是S的一個劃分。其中[x]R={y|y∈S,(x,y)∈R}為x所在的等價類。
性質1設(S,*,+)是一個有限Boole環,R是S上的一個同余關系。 ?X∈S/R,若X={x1,x2,…,xn},x1*x2*...*xn∈X。
證明?i,j,1≤i,j≤n,(xi,xj)∈R,由R是S上的一個同余關系及Boole環S的冪等性知:
(xi*xi*...*xi,x1*x2*...*xn)=(xi,x1*x2*...*xn)∈R因此x1*x2*...*xn∈X。
推論1設(S,*,+)是一個有限Boole環,R是S上的一個同余關系,則S關于R的每個同余類中均有最大元(對于≤1來說)。
證明設X∈S/R,其中X={x1,x2,…,xn},因為?x,y∈S,x≤1y?x*y=y,由性質2知,x1*x2*…*xn∈X。
推論2設(S,*,+)是一個有限Boole環,R是S上的一個同余關系,則S關于R的每個同余類中均有最小元(對于≤2來說)。
定義4設(S,*,+)是一個Boole環,≤是S的偏序關系。?x,y∈S,若映射C:S→S滿足
(1)x≤C(x);
(2)x≤y?C(x)≤C(y);
(3)C(C(x))=C(x)。
則稱C為Boole環S上的閉算子。
設C為Boole環S上的閉算子,x∈S,若C(x)=x,則稱x是C閉的。
定義5設(S,*,+)是一個Boole環,≤是S的偏序關系。?x,y∈S,若映射I:S→S滿足
(1)I(x)≤x;
(2)x≤y?I(x)≤I(y);
(3)I(I(x))=I(x)。
則稱I為Boole環S上的內部算子。
設I為Boole環S上的內部算子,x∈S,若I(x)=x,則稱x是I開的。
性質2設(S,*,+)是一個有限Boole環,R是S上的一個同余關系。?x∈S,記C(R)(x)=∨[x]R則C(R)是(S,*,+)上的閉算子,其中∨表示取最大元。
性質2顯然成立,證明從略。
設C(R)是(S,*,+)上的閉算子,CR表示S中所有C(R)閉元素所成的集合,即?x∈S,x∈CR?C(R)(x)=x。
性質3設(S,*,+)是一個有限Boole環,R是S上的一個同余關系。≤1與≤2是由(1)和(2)定義的兩個偏序,記
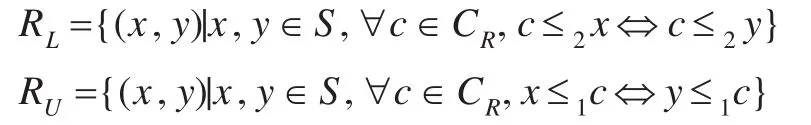
則:(1)RL是 Boole環 (S,*,+)上的一個同余關系;(2)RU=R。
證明(1)RL是S上的一個等價關系。設x,x′,y,y′∈S,(x,x′)∈RL,(y,y′)∈RL,若對c∈CR,c≤2inf{x,y},則c≤2x,c≤2y?c≤2x′,c≤2y′,所以c≤2inf{x′,y′}。
同理由c≤2inf{x′,y′}?c≤2inf{x,y}。因為
inf{x,y}=x*y,inf{x′,y′}=x′*y′
所以 (x*y,x′*y′)∈RL,即RL是S上的一個同余關系。
(2)因為[x]R必有一個元素x,使CR(x)=x,所以|CR|=|S/R|,且?c∈CR,c對于≤1是S中關于R同余類中的最大元,即 ?x,y∈S,(x,y)∈R?(x,y)∈RU,所以RU=R。
性質4設(S,*,+)是一個有限Boole環,R是S上的一個同余關系。 ?x∈S,記I(R)(x)=∧[x]R,則I(R)是(S,*,+)上的內部算子,其中∧表示取最小元。
證明以下分三個步驟證明:
(1)因為I(R)(x)是同余類[x]RL中的最小元,所以I(R)(x)≤2x。
(2)設x,y∈S,且x≤2y:
由 (x,I(R)(x))∈RL和 (y,I(R)(y))∈RL可 知 (x*y,I(R)(x)*I(R)(y))=(x,I(R)(x)*I(R)(y))∈RL。由(1)可知I(R)(x)≤2I(R)(x)*I(R)(y)= ∧{I(R)(x),I(R)(y)}≤2I(R)(y)。
(3)設x∈S,由I(R)(x)≤2x以及(2)的結論可知I(R)(I(R)(x))≤2I(R)(x)。因為 (x,I(R)(x))∈RL,(I(R)(x),I(R)(I(R)(x)))∈RL,由傳遞性知,(x,I(R)(I(R)(x)))∈RL,從而I(R)(x)≤2I(R)(I(R)(x)),故I(R)(I(R)(x))=I(R)(x)。
由此,I(R)是(S,*,+)上的內部算子。
用IR表示S中I(R)開元素全體構成的集合,即?x∈S,x∈IR?I(R)(x)=x。當x∈S且滿足C(R)(x)=I(R)(x)=x,稱元素x是開閉的。
定義6設(S,*,+)是具有最小元的有限Boole環,R是S上的一個同余關系,則稱(S,IR,CR)為同余近似空間。
設 (S,IR,CR)為同余近似空間,?c∈CR,由RL的表達式知,c是同余類[c]RL中的最小元,因此c∈IR,從而CR?IR,即?x∈S,x是開閉?x∈CR。
對于有限Boole環(S,*,+),可以證明S中有最大元,即1S∈S,而且1S=∨[1S]R,因此1S∈CR。
性質5設(S,IR,CR)為同余近似空間,則CR中有最小元。
證明因為S有最小元,所以∨[0S]R∈CR。?x′∈CR,若x′≠∨[0S]R,則存在x∈S,使得x′=∨[x]R。由 0S≤1x及閉算子的單調性,有∨[0S]R≤1x,即CR存在最小元∨[0S]R。
性質6設(S,IR,CR)為同余近似空間,則CR與IR均為完備格。
證明 由于CR?S是有限集,且具有最大元和最小元。因此,?X∈CR,supX與infX存在,即CR是完備格。又由于CR?IR,有 1S∈IR,由RL的定義,有∧[0S]RL=0S,即 0S∈IR,故IR是完備格。
2 同余近似空間的近似算子及性質
定義7 設(S,IR,CR)為同余近似空間,?x∈S,則
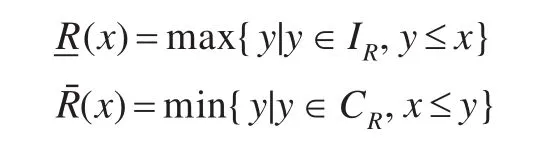
分別稱為x關于同余近似空間(S,IR,CR)的下近似集和上近似集,分別稱為下近似算子和上近似算子。
性質7 設(S,IR,CR)為同余近似空間,?x∈S,有:
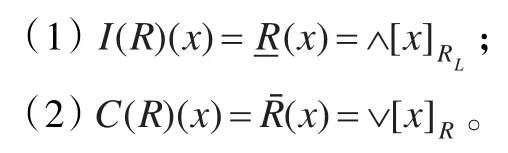
證明因為I(R)(x)=∧[x]RL∈IR,由算子I(R)的遞減性知I(R)(x)≤x,于是I(R)(x)≤max{y|y∈IR,y≤x}。
另一方面,?y∈IR,若y≤x,則y=I(R)(y)≤I(R)(x),從而 max{y|y∈IR,y≤x}≤I(R)(x),即(1)成立。
同理可證明(2)成立。
性質8 設 (S,IR,CR)為同余近似空間,?x,y∈S,近似算子和具有性質:
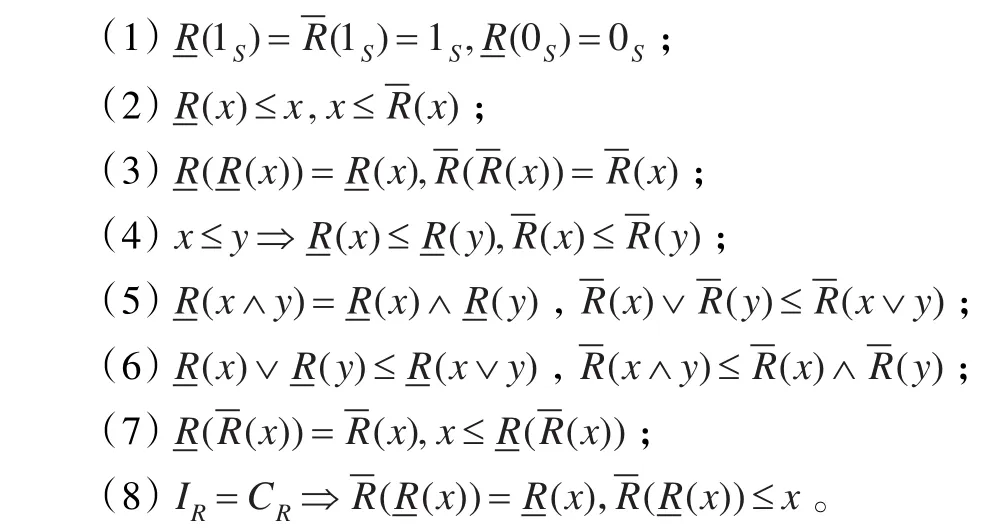
證明(1)(0S)=0S顯然,由于1S∈CR?IR,所以1S=∨[1S]R=(1S),(1S)=max{y|y∈IR,y≤1S}=1S。
由內部算子和閉包算子的性質,可知(2)、(3)、(4)成立。
下面證明(5)。
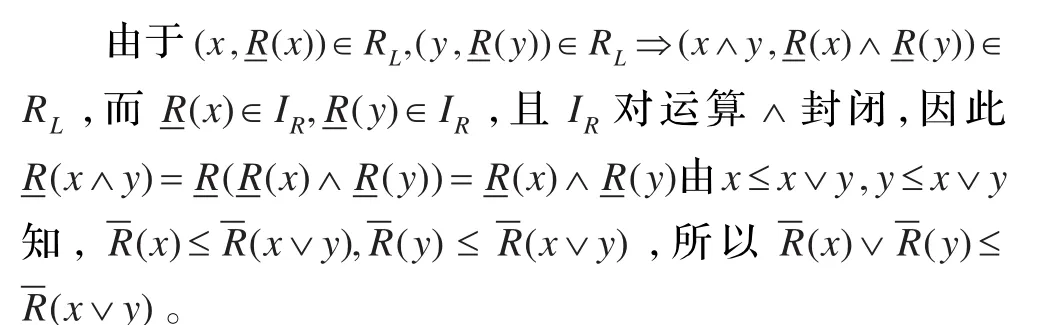

3 結語
本文從定義Boole環上的偏序關系入手,研究了Boole環上閉算子和內部算子的的性質,由此引入了同余近似空間和同余近似空間中上近似和下近似算子的定義,研究了上近似算子和下近似算子的性質。
[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Science,1982,11:341-356.
[2]Pawlak Z.Rough sets:theoretical aspects of reasoning about data[M].Boston:Kluwer Acadeic Publishers,1991.
[3]Iwinski T.Algebraic approach to rough sets[J].Bull Polish Acad Sci Math,1987,35:673-683.
[4]Pomykala J,Pomy J A.The stone algebra of rough sets[J].Bull Polish Acad Sci Math,1988,36:495-508.
[5]Yao Y Y.Twoviews of the theory of rough sets in finite universes[J].International Jour nal of Approx imate Reasoning,1996,15:291-317.
[6]Yao Y Y,Lin T Y.Generalization of rough sets using modallogic[J].Intelligent Automation and Soft Computing,1996,2:103-120.
[7]張化光,梁洪力.粗糙集的兩種新型算子及其Boolean代數性質[J].應用科學學報,2004,22(4):503-508.
[8]陳建飛,林公源.關于粗糙集的一點注記[J].云南民族學院學報:自然科學版,2002,11(2):65-67.
[9]陳世聯.粗糙集代數與蘊涵格[J].計算機工程與科學,2008(5):115-117.
[10]趙濤,秦克云.基于分子格的粗糙集模型推廣[J].計算機科學,2012,39(2):255-257.
[11]于佳麗,舒蘭.半群中粗理想的性質[J].電子科技大學學報,2002,31(5):539-541.
[12]林仁炳,王基一.粗糙群的同態性質[J].模式識別與人工智能,2006,19(3):338-341.
[13]張友,王書臣.粗糙子環的判定[J].大連民族學院學報,2009(1):29-31.
[14]盛德成.抽象代數[M].北京:科學出版社,2000:133-134.
[15]盛德成.抽象代數[M].北京:科學出版社,2000:83-84.

