基于弦長位置矩陣的目標識別

柴 華，楊明強

1.國家知識產權局專利局 專利審查協作北京中心，北京 100190

2.山東大學 信息科學與工程學院，濟南 250100

1 引言

在許多實際應用中，圖像并不是從相同的視點獲取的，經常發生視點的改變。視點的改變使得圖像往往經歷仿射變換甚至投射變換等相對較為復雜的幾何畸變，仿射變換相對于平移、旋轉、尺度變化等是對圖像幾何畸變的更為準確的逼近。因此，圖像分析和計算機視覺中對仿射不變性的研究越來越引起了國內外工程界的重視，仿射變換的不變性特征提取和識別研究具有更加重要的意義。現在，對于仿射不變特征的提取主要是提取用于識別目標的局部特征或者全局特征。在圖像處理中，仿射幾何的研究對象是圖像中的點、線、面。在仿射變換下，圖像中的點和線之間的關系存在著很多不變性，例如，平行不變、單比不變等等。仿射目標形狀識別就是利用從圖像中提取到的仿射不變特征，實現對目標形狀的檢測、定位與分類[1-2]。

常用的仿射不變目標識別的方法大體上可以分為以下幾類：

（1）用傅里葉描述子來表示輪廓形狀[3]。傅里葉描述子的優點在于目標圖像在有部分被遮擋的情況下，依然可以對目標圖像進行有效分類。傅里葉描述子很容易進行歸一化處理，以獲得具有旋轉、平移以及尺度不變的特征向量。輪廓上采樣點的數目，采樣點的間隔，量化誤差以及輪廓的擾動等等因素都會對基于傅里葉描述子的方法產生影響。

（2）用矩不變量來表示輪廓邊緣[4-5]。這種方法采用目標輪廓邊緣的矩不變量特征來實現目標的分類識別。其優點在于矩不變量不受目標模型和檢測圖像之間旋轉，平移以及尺度縮放的影響，同時計算量較小，速度較快。與傅里葉描述子的方法類似，矩不變量的方法也需要大量的數據庫進行訓練以獲得良好的識別結果。

（3）用幾何不變量表示仿射不變特征量。幾何不變量是目標圖像的內在信息，具有不隨著視點改變而發生改變的性質，因此近年來在計算機視覺領域越來越受到研究人員的重視。在目標識別中，用于簡單的二維目標形狀的識別的主要有幾何不變量包括代數不變量[6]、微分不變量[7-8]。

目標的形狀仿射相似不變特征提取可以根據圖像信息利用的程度分為基于全局不變特征的方法和基于局部不變特征的方法[9]。基于局部不變特征的方法和基于全局不變特征的方法具有各自的特點和適用領域。前者利用的是目標形狀的整體信息，通常計算量較大，但對于噪聲畸變相對敏感；后者僅是利用了目標形狀的局部信息，通常來說計算量較小，可用于實時性要求較高的應用場合，但是抗噪聲的能力相對較強[10-11]。目前，在仿射不變性特征提取方法的模型建立和適用性方面，建立起一種適用范圍廣、魯棒性強同時又能有效區分不同目標類別的方法還存在著相當大的困難[12-13]。

本文提出了一種基于目標形狀各個方向上的不同弦長的分布信息的弦長位置矩陣算法，用該算法提取的目標形狀特征具有仿射不變性。

2 弦長關聯統計算法

形狀特征是描述圖像內容的另一個重要特征，也是計算機視覺和模式識別研究的一個基本問題。形狀是物體的基本特征之一，用形狀特征區別物體非常直觀，利用形狀特征檢索圖像可以提高檢索的準確性和效率。形狀特征通常和目標聯系在一起，因而含有一定的語義信息，是圖像中最顯著的核心特征，可以有效地對圖像中感興趣的目標進行檢索。

弦長關聯算法的基本原理是利用統計學算法，根據形狀弦長的相關特性，統計形狀的各個方向的弦長，并用直方圖表示出來。各個方向的弦長統計直方圖形成弦長的相關矩陣，用該矩陣表示形狀特征[14]。該算法具有平移、旋轉和尺度變化不變性，并且對于輕微遮擋和噪聲干擾具有卓越的抵抗能力。弦長關聯統計算法可以處理各種類型的二維圖像，甚至是具有空洞或者被分為單獨的幾個部分的圖像。因此，可以應用該算法來從圖像中分割出感興趣的目標。該算法提出的形狀描述符與檢索方法還表現出具有圖像變換的不變性。由于該算法利用了圖像的統計特性，因此對單個樣本或少數幾個樣本取值的變化不是特別敏感，這就使得使用該算法提取的弦長特征量對目標圖像局部區域內的變化不敏感。因此，對于輕微遮擋的目標圖像，該算法也具有良好的識別效果。

但是該算法沒有考慮到仿射變換的影響，沒有特定的操作來抵抗仿射變換，在理論上缺乏對目標抵抗仿射變換能力的依據，在實驗中表現出的抵抗仿射變換能力不夠理想，主要原因之一是該算法統計弦長時僅作歸一化處理，未考慮到仿射變換對于各個方向平行弦間距的影響，同時沒有考慮到弦長分布的位置信息。本文對統計弦長的處理方法加以改進，完善其理論結構，進一步充分挖掘圖像目標的固有信息，使其在抗仿射變換方面取得突破，進一步提高該算法的性能。

3 弦長位置矩陣

弦長位置矩陣是利用表示弦長位置信息的三維矩陣來表示目標圖像的形狀特征，避免利用統計學的方法忽略了弦長位置的問題。首先，可以根據仿射變換前后封閉區域面積之比的特點來確定弦長的位置，將弦長的位置信息作為目標形狀識別的一個特征量。在統計各個方向的弦長時，由于目標的形狀特點或者內部存在空洞等原因，目標邊界上的兩點連線被分為若干部分，也就是同一位置上存在若干長度不同的弦，如圖1所示。

圖1 相同位置不同弦長示意圖

在記錄弦長時，應將同一位置的這些弦長分別記錄下來，然后按照弦的長度進行排序，將排序的信息作為位置信息的補充。因此，可以構造一個包含弦長位置信息的矩陣M[n，k，θ]來表示形狀特征，其中，n為弦長的位置信息，k為弦長的排序信息，θ為弦長的角度信息，矩陣的元素為歸一化的弦長。

3.1 弦長位置信息的統計

首先，將圖像采用閾值分割法進行二值化處理。將獲得的二值化圖像旋轉θi角度。假設θi方向上的弦長集合由 C={ci，n/n∈[1，N]}表示，其中N是各個方向上弦的數量。

弦長的位置根據仿射變換前后封閉區域面積之比不發生改變的特點來確定。當從固定的方向進行弦長統計時，弦長的位置可用一系列參數標號來表示。根據弦長統計的特點，此處采用統計弦長和的方法來計算區域面積。弦長利用弦與形狀邊界的交點之間的歐式距離進行計算。

為了避免統計過程中的累積誤差，利用第n條弦與圖像起始邊界組成的封閉區域面積來統計第n條弦ci，n的位置，按照下面的公式計算

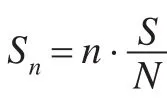
3.2 弦長位置的仿射不變性

圖2 旋轉θi角度后目標形狀平行弦位置

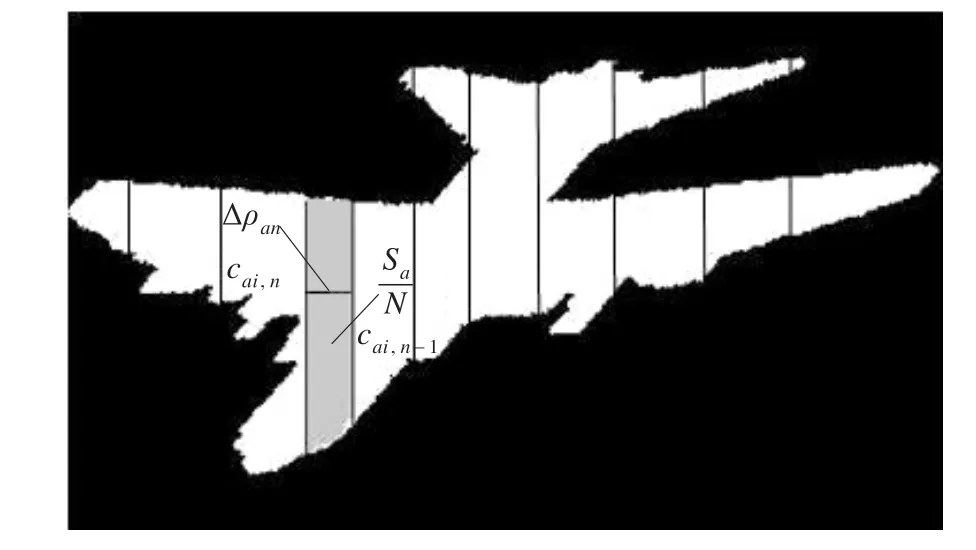
圖3 經過仿射變換旋轉θai角度后目標形狀平行弦位置

由圖2和圖3可以看出，兩條相鄰平行弦間的面積與整體面積之比不發生改變，因此，弦長的相對位置，即弦長的位置標記n，在仿射變換之后不發生改變。

3.3 弦長位置矩陣的構造

確定弦ci，n的位置之后，統計在該位置上所有弦長的信息。假設弦ci，n與形狀邊界依次交于點p1(x1，y1)，p2(x2，y2)，…，pm(xm，ym)，m=2k。位于弦ci，n的位置上的第j條弦的長度利用該弦與形狀邊界的交點p2j與p2j-1之間的歐氏距離表示，即

令向量 D為在弦ci，n位置上所有弦長的集合D={L1，L2，…，Lk}，將 D內的元素按照弦長進行降序排列，得到排序后的集合 D′={L′1，L′2，…，L′k}。如果將角度θ的范圍[0，179]均勻量化為F個區間，當弦長位置序號n從1增加到N，角度θ從增加0到θF，可以獲得N×F個弦長集合，將這些弦長集合進行排列，組成弦長位置矩陣M。

按照上述方法，統計各個方向的弦長以及位置信息的特征，形成弦長位置特征矩陣M[n，k，θ]。為了進一步增強提取的形狀特征矩陣對于仿射變換的抵抗能力，對弦長特征矩陣 M[n，k，θ]中的弦長采用相對弦長進行歸一化處理。此處的相對弦長是絕對弦長與矩陣中的最大弦長的比值，即

其中，Lmax，i為θi方向上的最大弦長。

4 相似性測度

本文的相似性測度采用動態空間彎折匹配算法（DSW）[15]，動態空間彎折匹配算法是基于動態時間彎折距離（DTW）的非線性技術的算法。

當提取的形狀特征序列Q和G不具有相同的維數，同時具有彎折的情況時，通常采用動態時間彎折距離來度量特征之間的相似性。動態時間彎折距離基于兩個特征序列中的各點間的非剛性排列，它允許特征序列中的點進行復制后再進行對齊匹配。

定義n行m列矩陣T為時間序列Q和G的距離矩陣，矩陣T中的元素為不同時間序列數據對象之間的點的歐氏距離：

其中，d(qi，gi)是兩個時間序列數據點之間的距離值，可以認為是對象q與g之間相異性的量化表示。

為了矩陣處理方便，應該把彎曲路徑的擺動范圍限制在距離矩陣的對角線兩側附近，因此，在不考慮區域外的距離相似因子的情況下稱這種彎曲路徑的子集為彎曲窗口。通過預先設定的寬度為w的對角彎曲窗口進行查找的動態時間彎曲距離dDTW(Q，G)由下列公式定義：

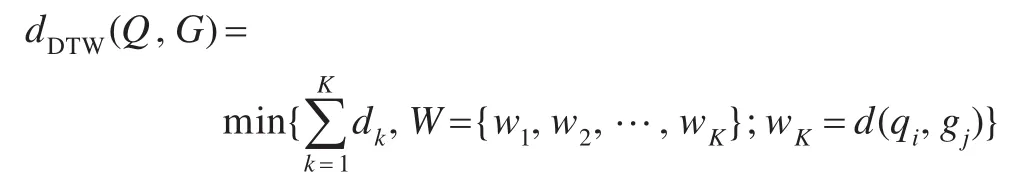
動態空間彎折距離按照下列公式進行定義[9]：

其中，LQG是最小彎曲路徑在距離矩陣T中經過的元素的個數。

在進行相似性比較時，首先計算查詢圖像與模板圖像的弦長位置矩陣 MT[n，k，θ]與 MQ[n，k，θ]中每個方向上位于相同位置的最大弦長之間的距離，即計算二維矩陣 MT[n，1，θ]與 MQ[n，1，θ]之間的距離d1：

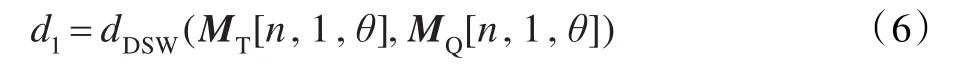
在一般情況下，利用d1可以識別出大部分目標圖像。此處，還可以根據不同的計算精度要求來選擇需要計算的二維矩陣 M[n，i，θ]之間的距離di：

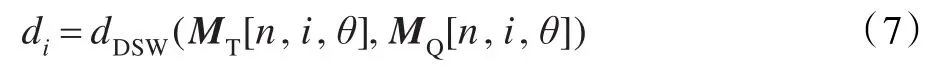
將計算得到的距離d1d2…di進行加權求和，得到最終的判決距離DistM：

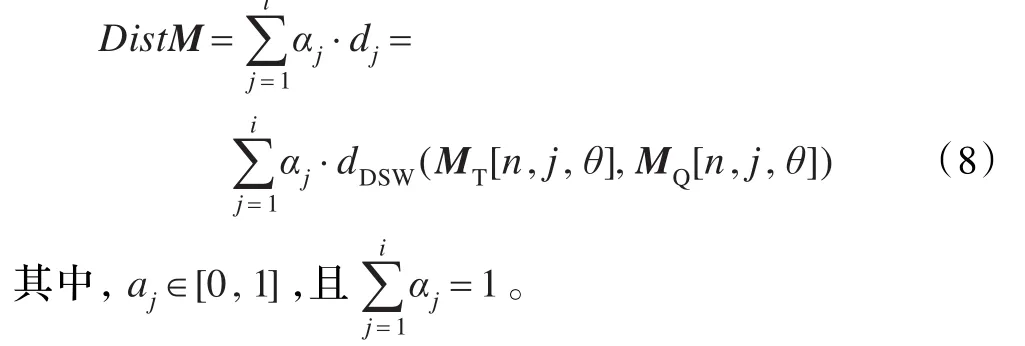
5 實驗結果

在軍事科技的應用中，從獲取的目標圖像中能夠快速地區分出不同的飛行器類型以及飛行器的不同飛行姿態具有十分重要的意義。實驗采用實際的飛行器圖像來驗證本文提出的算法的形狀描述能力，利用弦長位置矩陣提取的仿射不變特征進行飛行器圖像識別。在本文實驗中采用在文獻[16]中采用的相同的飛行器數據庫，模板圖像的輪廓經過任意的仿射變換產生測試圖像。模板圖像和測試圖像如圖4所示。

圖4 模板圖像和相應的測試圖像

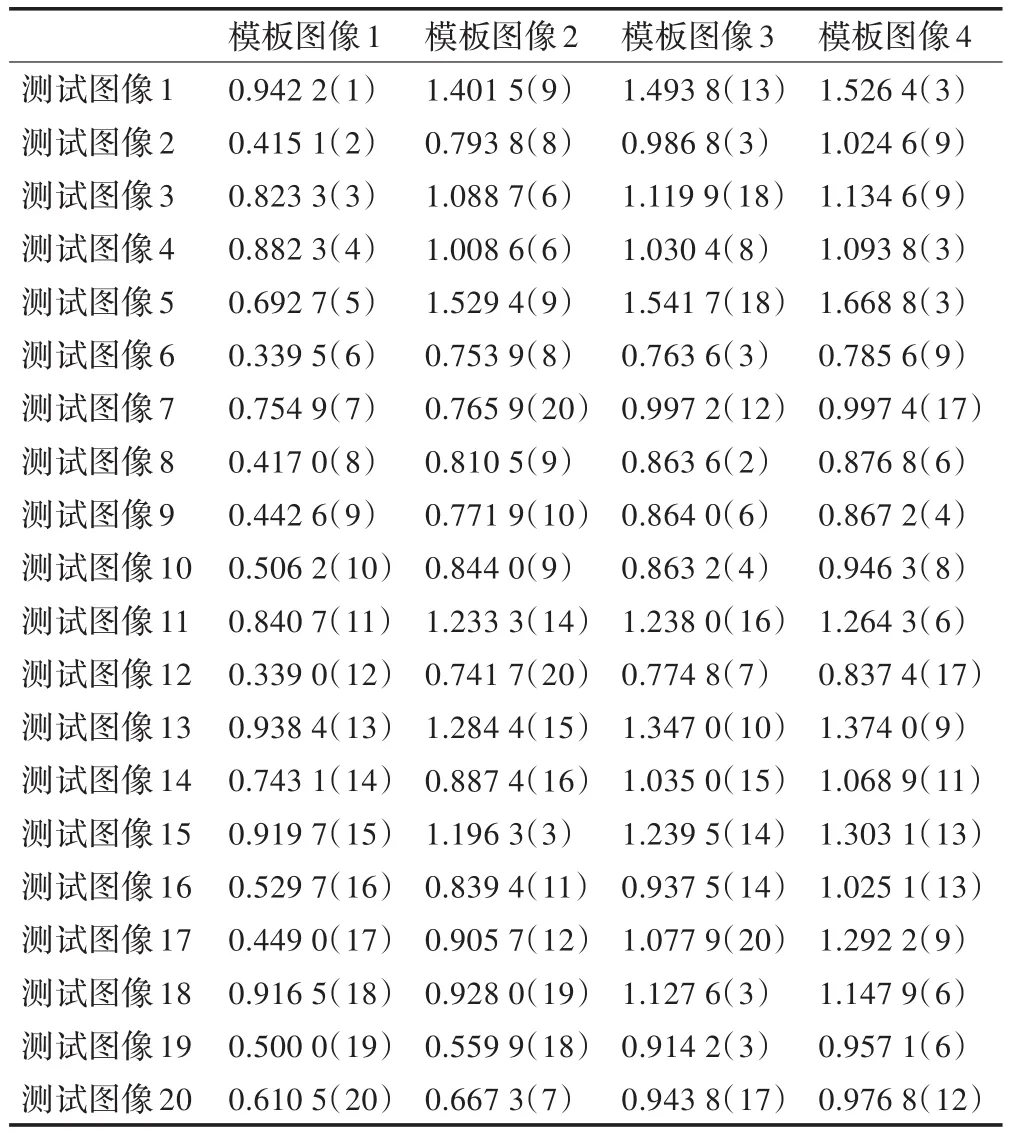
表1 最接近的4幅模板圖像的動態空間彎折距離

表1給出了與每幅測試圖像最接近的4幅模板圖像的動態空間彎折距離。其中，按照公式（8）定義的測試圖像與模板圖像之間的動態空間彎折距離列在表的4列中。第1列為與對應的測試圖像最為匹配的模板圖像的動態空間彎折距離。兩幅圖像的動態空間彎折距離越小，則說明兩幅圖像的相似程度越高，多幅圖像中與其動態空間彎折距離最小的圖像為與其最為相似的圖像，表1中動態空間彎折距離數值后括號內的標號為與該距離數值對應的模板圖像的標號，由實驗結果可以看出，與測試圖像相比動態空間彎折距離最小的模板圖像是與其對應的進行仿射變換之前的模板圖像，由此可見，測試圖像可以被正確地識別，識別率可以達到100%。而弦長關聯統計算法則沒有考慮到弦長位置的變化，對于仿射變換無法抵抗，對仿射變換之后的測試圖像無法正確識別出相應的模板圖像，識別率為0。實驗結果表明弦長位置矩陣是一種有效的形狀描述方法，對于仿射變換具有良好的魯棒性。

6 結束語

提出了一種基于弦長位置矩陣的形狀特征提取算法，通過統計目標形狀各個方向上的弦長位置信息和不同弦長的排序信息來構造仿射不變特征量，利用弦長位置矩陣來表示目標形狀的特征。本文算法易于實現，在識別性能上是優越的。實驗結果表明該算法提取的形狀特征具有良好的仿射不變性，與弦長關聯統計算法相比較，本文提出的算法在抵抗仿射變換方面具有卓越的表現。

[1]章毓晉.圖像工程[M].北京：清華大學出版社，2000.

[2]許錄平.數字圖像處理[M].北京：科學出版社，2007.

[3]Zhang Shaoting，Zhan Yiqiang，Zhou Yan，et al.Efficient sparse shape composition with its applications in biomedical image analysis：an overview[C]//Proceedings of the 9th IEEE International Symposium on Biomedical Imaging（ISBI），2012：976-979.

[4]Hu M K.Visual pattern recognition by moment invariant[J].IRE Trans on Information Theory，1962，8（2）：179-187.

[5]Khotanzad A，Hung Y H.Invariant image recognition by Zemike moments[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12（5）：489-497.

[6]Forsyth D A，Mundy J L.Invariant descriptor for 3-D object recognition and pose[J].IEEE Trans on Pattern Anal Mach Intell，1991，13（10）：971-991.

[7]Weiss I.Noise-resistant invariant of curves[J].IEEE Trans on Pattern Anal Mach Intell，1993，15（9）：943-948.

[8]Weiss I.Geometric invariants and object recognition[J].Int J Comput Vision，1993，10（3）：207-231.

[9]陳濤.圖像仿射不變特征提取方法研究[D].長沙：國防科學技術大學，2006.

[10]呂玉增.形狀仿射不變特征提取與識別研究[D].長沙：國防科學技術大學，2008.

[11]孫即祥.模式識別中的特征提取與計算機視覺不變量[M].長沙：國防工業出版社，2001.

[12]Lazebnik S，Sehmid C，Ponce J.A sparse texture representation using affine-invariantregions[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition，2003：319-324.

[13]Rothganger F，Lazebnik S，Schmid C，et al.3D object modeling and recognition using affine invariant patches and multi-view spatial constraints[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition，2003：272-277.

[14]Yang Mingqiang，Kidiyo K，Joseph R.Shape matching and object recognition using Chord contexts[C]//Proceedings of 2008 International Conference on Visualisation，9-11 July，2008：63-69.

[15]Yang Mingqiang.Shape-based feature extraction and similarity matching[D].France：INSA，2008.

[16]Dudani S A.Aircraft identification by moment invariants[J].IEEE Trans on Comput，1997，21：39-46.