乘積季節(jié)ARIMA模型的建立及其在河南省甲型病毒性肝炎發(fā)病數(shù)預(yù)測中的應(yīng)用

李軍，史魯斌，肖占沛

河南省疾病預(yù)防控制中心，河南鄭州 450016

甲型病毒性肝炎（甲肝）是由甲肝病毒引起的以肝臟損害為主的消化系統(tǒng)傳染性疾病，主要經(jīng)糞—口途徑傳播；隨著甲肝疫苗預(yù)防接種的推廣和衛(wèi)生狀況的改善，河南省甲肝的發(fā)病率逐年下降，但仍存在不同程度的甲肝流行以及局部地區(qū)的暴發(fā)[1]。傳染病的流行狀況往往受到經(jīng)濟(jì)水平、社會環(huán)境和生活方式、針對性的疫苗接種率等多種因素的影響。近幾年來國內(nèi)外有研究者[2-5]利用疫情監(jiān)測數(shù)據(jù)構(gòu)建ARIMA模型，預(yù)測傳染病的發(fā)病趨勢，取得較好的預(yù)測效果。該研究將利用河南省2008—2013年分月甲肝疫情監(jiān)測數(shù)據(jù)建立ARIMA模型，并利用2014年的監(jiān)測數(shù)據(jù)評價ARIMA模型的預(yù)測效果。

1 資料與方法

1.1 資料來源

疫情數(shù)據(jù)來源于中國疾病預(yù)防控制信息系統(tǒng)中河南省2008～2013年分月的甲肝監(jiān)測數(shù)據(jù)。

1.2 研究方法

采樣時間序列法，利用河南省2008—2013年分月的甲肝疫情監(jiān)測資料，通過SAS 9.1統(tǒng)計軟件，建立甲肝發(fā)病的ARIMA模型的多個模型，篩出最優(yōu)模型，利用2014年1—12月的甲肝疫情資料評價該模型的預(yù)測效果。ARIMA模型分為自回歸模型（AR)、移動平均模型（MA)、ARIMA模型[6]。

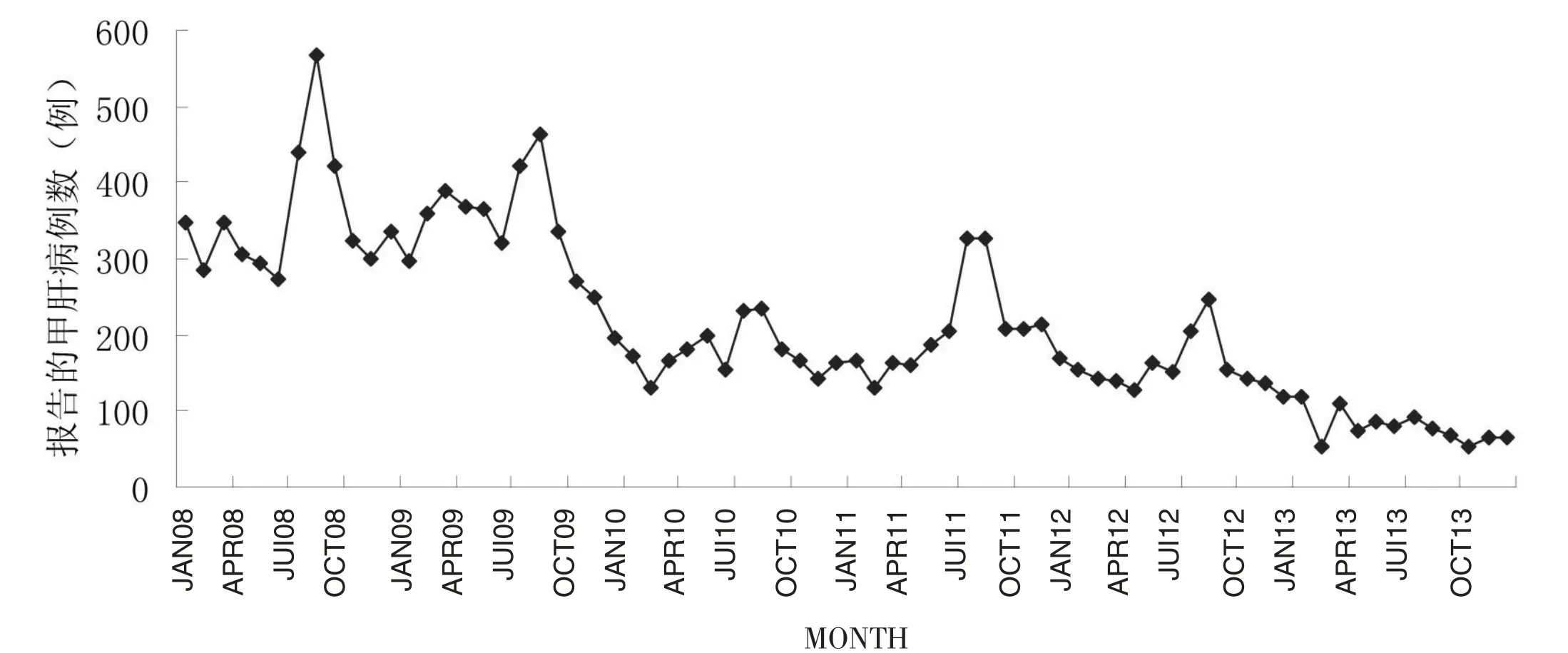
圖1 2008—2013年河南省報告的甲肝病例數(shù)按月分布圖

一般ARIMA建模包括模型的識別、參數(shù)估計、模型檢驗3個步驟，依據(jù)河南省2008—2013年甲肝分月的監(jiān)測數(shù)據(jù)，通過這3個步驟反復(fù)建模，篩選出最優(yōu)的預(yù)測模型。

①模型識別：觀察2008—2013年甲肝分月監(jiān)測數(shù)據(jù)的時間序列的平穩(wěn)性，如若是非平穩(wěn)序列，要通過數(shù)據(jù)轉(zhuǎn)化和一階周期為12的季節(jié)性差分將序列平穩(wěn)化。先對序列的季節(jié)性成分進(jìn)行分析，再識別非季節(jié)性成分，通過觀察序列的自相關(guān)系數(shù)和偏相關(guān)系數(shù)初步確定階值。

②參數(shù)估計：模型參數(shù)估計運用最大似然法或最小二乘法，根據(jù)序列的自相關(guān)系數(shù)和偏相關(guān)系數(shù)，經(jīng)過不同方法的參數(shù)選擇、比較、篩選，計算出自回歸移動平均過程的系數(shù)，并對其標(biāo)準(zhǔn)誤進(jìn)行假設(shè)檢驗。

③模型檢驗：一個合適的模型的殘差序列是白噪音過程，其自相關(guān)系數(shù)（autocorrelation function，ACF）和偏向相關(guān)系數(shù)（partial autocorrelation function，PACF）應(yīng)與0無統(tǒng)計學(xué)差異，利用此標(biāo)準(zhǔn)對所建立的ARIMA模型是否合適作出診斷。若幾個模型都能滿足要求，選取Akaike信息準(zhǔn)則 （Akaike information criterion，AIC）和Schwarz貝葉斯準(zhǔn)則（Schwarz Bayesian information criterion，SBC）、殘差序列的方差（Variance estimate，VE）以及方差估計的平方根（standard error estimate，std.EE）較小者，則模型效果較好[7]。

2 結(jié)果

2.1 河南省2008—2013年甲肝報告病例數(shù)的變化趨勢

河南省2008—2013年甲肝報告病例數(shù)呈現(xiàn)明顯的季節(jié)性，每年的6～9月呈現(xiàn)發(fā)病高峰，11月至次年3月呈現(xiàn)發(fā)病低谷，且呈現(xiàn)逐年遞減趨勢，提示該時間序列為非平穩(wěn)序列。2008—2013年河南省報告的甲肝病例數(shù)按月分布情況見圖1。

2.2 模型識別結(jié)果

在對原始數(shù)據(jù)進(jìn)行對數(shù)轉(zhuǎn)換的基礎(chǔ)上進(jìn)行了一階差分和一階周期為12的季節(jié)性差分，將序列平穩(wěn)化，生成數(shù)據(jù)系列（圖2），圖2的圖形顯示差分后序列近似平穩(wěn)。延遲1階和12階的自相關(guān)系數(shù)顯著大于可信區(qū)間范圍，說明差分后仍具有短期相關(guān)性和明顯的季節(jié)性，考慮擬合ARIMA乘積季節(jié)模型。

2.3 參數(shù)估計結(jié)果

經(jīng)過參數(shù)比較和選擇，根據(jù)AIC和SBC的最小的準(zhǔn)則和模型簡潔原則，初步判斷為模型ARIMA(1,1,0)(2,1,2)，見表1。

表1 各模型的擬合優(yōu)度統(tǒng)計量

2.4 模型的檢驗結(jié)果

模型ARIMA(1,1,0)(2,1,2)延遲6階、12階、18階、24階、30階、36階X2檢驗統(tǒng)計量的P均＞0.05，表明模型對數(shù)據(jù)信息提取充分，擬合效果較好，見圖3。

3 討論

某地甲肝的暴發(fā)流行與當(dāng)?shù)氐慕?jīng)濟(jì)、衛(wèi)生、甲肝疫苗接種等有關(guān)。由于受諸多因素的影響，甲肝暴發(fā)或者流行的早期預(yù)警尤為重要。

傳統(tǒng)的甲肝預(yù)測預(yù)警模型可以分為兩類：回歸分析模型和時間序列模型。前者由于受到各種未知因素的影響、難以獲得足夠的數(shù)據(jù)進(jìn)行分析，因此有一定的局限性。后者將已知的、未知的因素綜合成一個統(tǒng)一的因素，將這些因素蘊含在時間序列這個變量中，所需的原始資料較少，對疾病短期內(nèi)的預(yù)測效果較好，具有一定的應(yīng)用前景[8-10]。

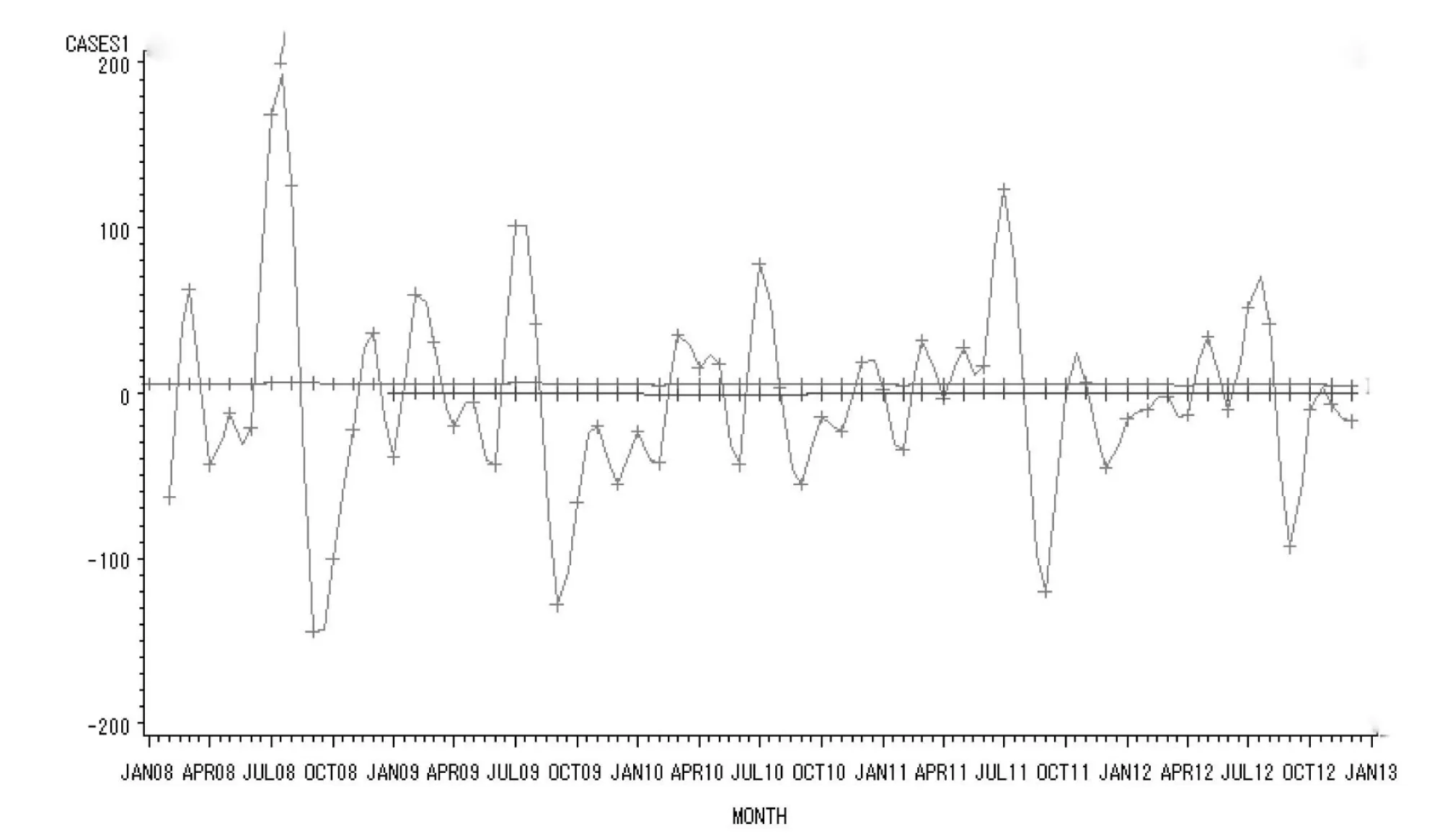
圖2 1階與12步差分和對數(shù)轉(zhuǎn)換后序列圖

圖3 河南省甲肝按月報告病例數(shù)的擬合效果圖

該研究對河南省2008—2013年的甲肝監(jiān)測數(shù)據(jù)資料進(jìn)行擬合建模，結(jié)果顯示，河南省2008—2013年的甲肝監(jiān)測數(shù)據(jù)呈現(xiàn)逐年降低的趨勢，且具有明顯的季節(jié)性周期。篩選ARIMA（1，1，0）（2，1，2）12模型為最優(yōu)模型，利用此模型對2014年1—12月的甲肝監(jiān)測數(shù)據(jù)進(jìn)行預(yù)測，結(jié)果顯示預(yù)測值與真實值接近，提示該模型有較好的預(yù)測效果，在河南省甲肝發(fā)病預(yù)測中具有較高的推廣應(yīng)用價值，可為河南省甲肝的防控措施及預(yù)警機制提供參考。

[1]朱奕奕，馮瑋，趙琦，等.ARIMA乘積季節(jié)模型在上海市甲肝發(fā)病預(yù)測中的應(yīng)用[J].復(fù)旦學(xué)報：醫(yī)學(xué)版，2012,39（5）：460-464.

[2]楊召，葉中輝，尤愛國，等.乘積季節(jié)ARIMA模型在結(jié)核病發(fā)病預(yù)測中的應(yīng)用[J].中國公共衛(wèi)生，2013,29（4）：469-472.

[3]彭志行，鮑昌俊，趙楊,等.ARIMA乘積季節(jié)模型及其在傳染病發(fā)病預(yù)測中的應(yīng)用[J].數(shù)理統(tǒng)計與管理，2008,27（2）：362-368.

[4]金如鋒，邱紅，周霞,等.ARIMA模型和GM(1，1)模型預(yù)測全國3種腸道傳染病發(fā)病率[J].復(fù)旦學(xué)報：醫(yī)學(xué)版，2008,35（5）：675-680.

[5]時照華，蘇虹，秦鳳云,等.ARIMA模型在常見呼吸道傳染病疫情預(yù)測中的應(yīng)用[J].安徽醫(yī)科大學(xué)報，2013,48（7）：783-785.

[6]黃春萍，鄧晶，張磊,等.ARIMA模型在麻疹預(yù)警中的應(yīng)用[J].疾病監(jiān)測，2008,23（1）：53-55.

[7]李永紅，林枚，董柏青,等.ARIMA模型在細(xì)菌性痢疾預(yù)測中的應(yīng)用[J].現(xiàn)代預(yù)防醫(yī)學(xué)，2010,37（7）：1203-1204.

[8]葉孟良，李智濤，歐榮.ARIMA模型在預(yù)測重慶市醫(yī)院日住院量中的應(yīng)用[J].重慶醫(yī)學(xué)，2012,41（13）：1260-1261.

[9]牟瑾，謝旭，李媛,等.將ARIMA模型應(yīng)用于深圳市1980-2007年重點法定傳染病預(yù)測分析[J].預(yù)防醫(yī)學(xué)論壇，2009,15（11）：1051-1052.

[10]張彥琦，唐貴立，王文昌,等.ARIMA模型及其在肺結(jié)核預(yù)測中的應(yīng)用[J].現(xiàn)代預(yù)防醫(yī)學(xué)，2008,35（9）：1608-1612.