Timoshenko梁靜力學和動力學問題有限體積法求解

井麗龍,張文平,明平劍,付麗榮,劉曉剛

(哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001)

Timoshenko梁靜力學和動力學問題有限體積法求解

井麗龍,張文平,明平劍,付麗榮,劉曉剛

(哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001)

為探究Timoshenko梁模型數(shù)值計算方法，開展了基于有限體積法的Timoshenko梁數(shù)值計算方法研究。利用有限體積法對考慮剪切變形的梁進行了離散，并進行了靜力學分析和動力學分析，通過幾個經(jīng)典算例將此方法所得到的數(shù)值解與解析解及有限元解進行了對比，結(jié)果證明，有限體積法有較高精度。與此同時利用有限體積法離散Timoshenko梁時當梁為細長梁時不存在剪切自鎖現(xiàn)象。有限體積法可以應(yīng)用于Timoshenko梁模型靜力彎曲分析、固有特性和動力響應(yīng)分析。

有限體積法；Timoshenko梁；靜力學；動力學；剪切自鎖現(xiàn)象; 固有頻率；位移響應(yīng)

在有限元結(jié)構(gòu)分析中，深梁和中厚板剪切自鎖是比較突出的問題，它通常給出較大誤差的結(jié)果來掩蓋真實的求解值。如果不仔細對結(jié)果進行分析，帶來的后果是十分嚴重的。尤其是對于應(yīng)用廣泛的梁、板、殼體結(jié)構(gòu)，彎曲變形是主要變形形式，不合理的剪切自鎖將帶來巨大誤差的分析結(jié)果。做任何復雜的工程分析前，有必要對自鎖問題進行分析。有限元方法中常采用減縮積分單元、全積分二階單元、一階單元細密格式和Wilson非協(xié)調(diào)模式[1]來解決此問題且相對復雜，而有限體積法卻有著獨特的性質(zhì)即對于Timoshenko梁模型在分析細長梁時不存在剪切自鎖現(xiàn)象，其原因是有限體積法所列的方程來自于對各控制體廣義力平衡方程，計算中沒有有限元法中數(shù)值積分這一過程，因此不存在有限元中出現(xiàn)的剪切自鎖現(xiàn)象，進而有必要研究基于有限體積法對Timoshenko梁在不同跨高比下的靜力學與動力學研究。有限體積法作為一種數(shù)值計算的方法多應(yīng)用于流體、傳熱等領(lǐng)域[2-6]，其在結(jié)構(gòu)計算方面的應(yīng)用較少。Demirdzic等采用有限體積法，在處理固體力學離散單元間位移分布時，提出了將一個單元與周圍單元位移采用線性分布，通過用常應(yīng)變平面單元平均分配兩個單元之間的位移計算出應(yīng)變，并奠定了有限體積法應(yīng)用于結(jié)構(gòu)分析的基礎(chǔ)。Wheel采用單元與每個面單元間位移線性分布假設(shè)，并對Mindlin板進行了分析，其結(jié)果認為采用中厚板模型模擬薄板時沒有“自鎖現(xiàn)象”。在用有限元法對大跨高比Timoshenko梁模型分析時會出現(xiàn)剪切自鎖現(xiàn)象，即梁過度剛硬不發(fā)生彎曲變形只有零解，這是由于約束條件未能精確滿足，在梁很薄時導致不確定地夸大了剪切應(yīng)變能項的量級而造成的，在梁、板、殼的有限元分析中，此種現(xiàn)象稱為剪切自鎖現(xiàn)象，而利用有限體積法解決考慮剪切變形的梁、板模型時卻不存在剪切自鎖現(xiàn)象[7-8]。

本文利用有限體積法基于Timoshenko梁模型對不同跨高比的梁進行了靜力分析[8]，固有頻率提取和動力響應(yīng)分析驗證了有限體積法能夠?qū)imoshenko梁模型進行較精確的模擬并展現(xiàn)出此方法不存在剪切自鎖的現(xiàn)象。

1 控制方程

1.1 平衡方程

(1)

式中:σ是應(yīng)力張量，F(xiàn)是體力向量，u是位移向量。當問題為靜力問題時慣性力為零。

1.2 本構(gòu)方程

Timoshenko梁理論源自1921年Timoshenko提出的及剪切變形的梁修正理論，在分析中將剪切變形和轉(zhuǎn)動慣量考慮進去。Timoshenko梁模型適合于描述短梁、層合梁受高頻激勵所引起的振動現(xiàn)象。

由材料力學的基本公式可知：

(2)

式中：M、Q為彎矩和剪力，E為楊氏模量，I為截面慣性矩，ψ為彎矩引起的轉(zhuǎn)角，w為撓度，k'為剪切修正系數(shù)(矩形截面時取0.833)[9]，A為截面面積，G為剪切彈性模量。

2 數(shù)值方法

對于Timoshenko梁模型，此模型為一維模型，對于梁的狀態(tài)用兩個變量(撓度w和截面轉(zhuǎn)角ψ)描述。對于此一維模型本文采取的是均勻網(wǎng)格來進行計算，如果要進行非均勻一維網(wǎng)格的相關(guān)計算可引入等參單元再進行相應(yīng)計算。

本文采用的是兩節(jié)點一維控制體對梁模型進行離散，基于有限體積法中的格心法將兩個變量(撓度w和截面轉(zhuǎn)角ψ)存儲于控制體中心，控制體之

間界面的值可通過相鄰兩個控制體中心變量的插值得到。控制體離散示意圖如下圖1所示。取其中一個控制體，其受力如圖2所示。

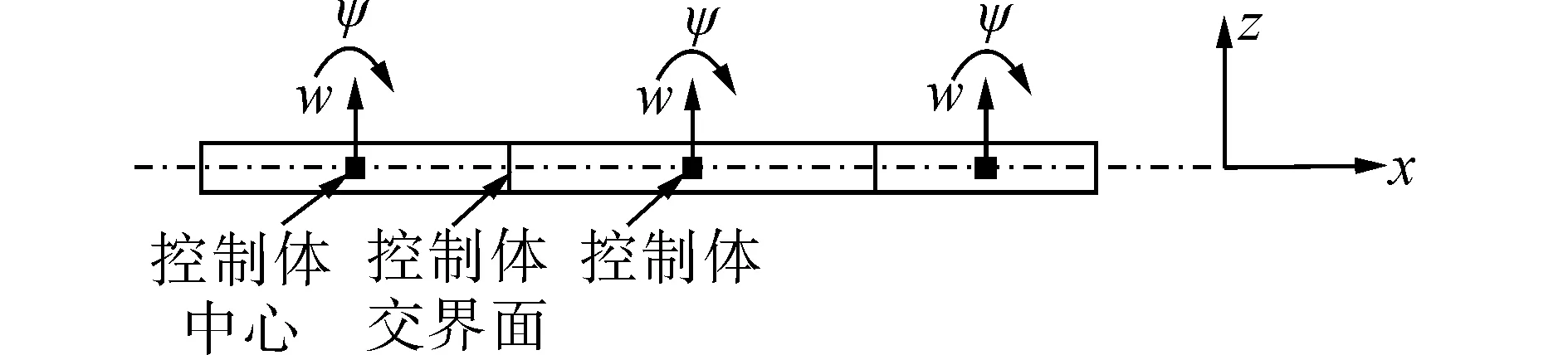
圖1 控制體離散示意圖Fig. 1 Discrete control volume

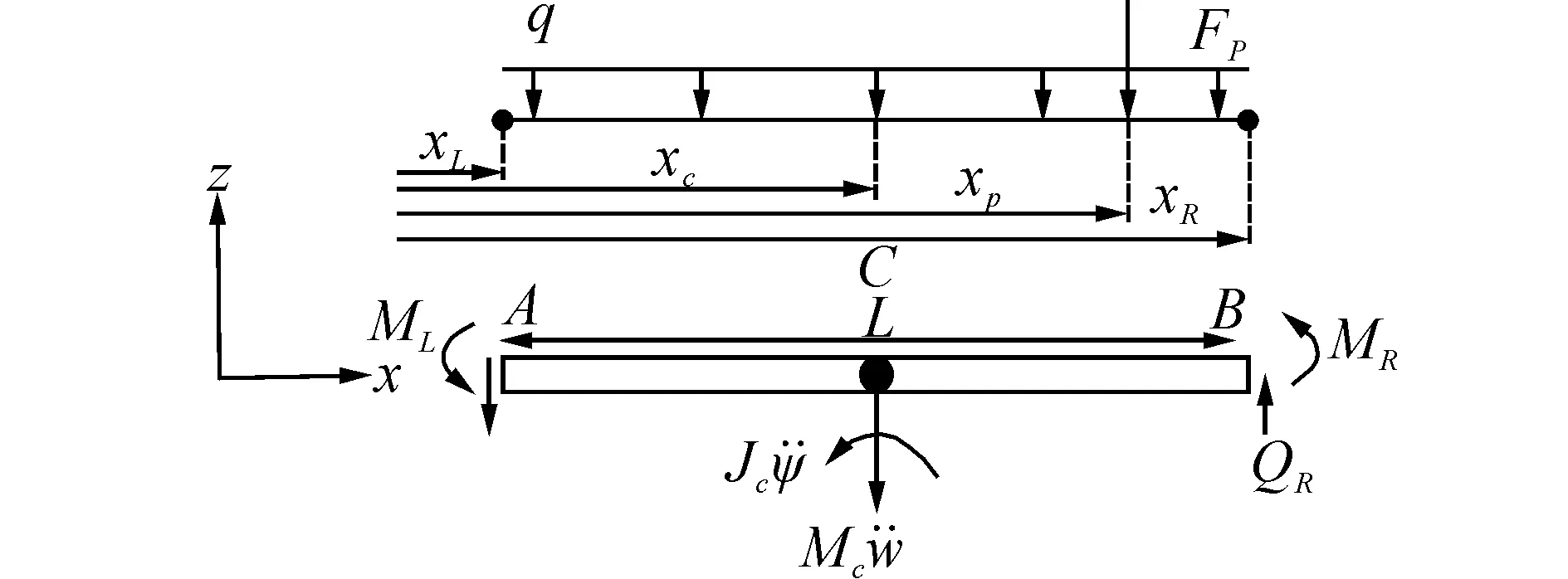
圖2 控制體受力示意圖Fig. 2 A control volume under internal and external loads

其廣義力平衡方程為

(3)

式中：n為法向方向(+1或者-1)，Mc、Jc分別為單元質(zhì)量和轉(zhuǎn)動慣量，M、Q分別是彎矩、剪力，q為均布載荷，F(xiàn)p為集中載荷，由于小變形假設(shè)cosθi=1。

將方程(2)代入式(3)，可得到關(guān)于撓度w和截面轉(zhuǎn)角ψ為未知量的方程組：

(4)

對于方程中的dψ/dx和dw/dx項采用線性插值的方法進行近似。

圖3 控制體變量示意圖Fig. 3 Variable of the control volume

假設(shè)i為第i個節(jié)點，則角標i表示各節(jié)點變量，假設(shè)ic表示第i個控制體中心變量，如圖3所示，則根據(jù)線性插值可以得到

(5)

邊界控制體處理：

左邊界控制體

(6)

右邊界控制體

(7)

對于邊界條件處理：兩端簡支，w1=0,M1=0,wn+1=0,Mn+1=0；兩端固支，w1=0,ψ1=0,wn+1=0,ψn+1=0；一端固支一端自由，固支端采用與上式相同式子，自由端Mn+1=0,Qn+1=0推導出廣義位移的關(guān)系。

通過對所有離散單元列平衡方程可以得到求解梁方程的一般矩陣形式，其壓縮形式如下：

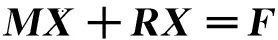
(8)

2.1 靜力學分析

對于靜力學問題，其中一個控制體其廣義力平衡方程與式(3)類似，令慣性力為零即可得到

RX=F

(9)

式中：R為2n×2n對稱帶狀矩陣，與幾何參數(shù)材料參數(shù)有關(guān)；X為廣義位移(各控制體中心的撓度與轉(zhuǎn)角)；F為廣義載荷(等效的力與彎矩，通過力平衡將其等效)，線性方程組的求解采用一般的數(shù)值解法即可實現(xiàn)如高斯消去法。

2.2 固有頻率提取

對于Timoshenko梁模型，其自由振動方程為式(8)去掉外載荷項。由梁的理論可假設(shè)位移響應(yīng)滿足如下關(guān)系：

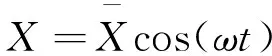
(10)

則可推導出頻率方程：

(11)

利用QR分解法可求得相應(yīng)的特征值，開平方即為相應(yīng)的固有頻率。

2.3 動力響應(yīng)分析

當梁受到外部激勵時，它將產(chǎn)生動力響應(yīng)，由于彈性體的振型具有正交性，因此可以用模態(tài)分析法，方便地求得彈性體對外部激勵的響應(yīng)，當用有限體積法進行近似時主要基于以下思路：

1) 應(yīng)用達朗貝爾原理對每個離散后的控制體建立廣義力平衡方程：∑Mc=0,∑Fz=0。

2) 集成所有控制體形成整個梁的廣義力平衡方程進而形成振動方程，形式如式(8),此式左邊各項見固有頻率分析，F(xiàn)代表外部受到的激勵f(x,t)。

3) 對相應(yīng)時間項x(x,t)的求解采用經(jīng)典的中心差分法[9]進行求解。

3 算例

3.1 懸臂梁受均布載荷靜力分析

均布載荷Q=100 N/m;梁長L=1 m;梁寬T=0.02 m；梁高為H;剪切修正系數(shù)Ks=0.833; 楊氏模量E=210 GPa;泊松比0.3。

懸臂梁撓度曲線表達式[10]：

(12)

式中:α為剪切系數(shù)[10]。計算了3種跨高比的撓度：選擇梁截面高度為0.008m，寬度為0.02m，跨高比為125，計算結(jié)果如圖5(a)。其次選擇梁截面高度為0.02m，寬度為0.02m，跨高比為50，計算結(jié)果如圖5(b)。最后選擇梁截面高度為0.2m，寬度為0.01m，跨高比為5，計算結(jié)果如圖5(c)。

圖4 懸臂梁示意圖Fig. 4 Cantilever beam under equal distributing loads

(a) L/H=125

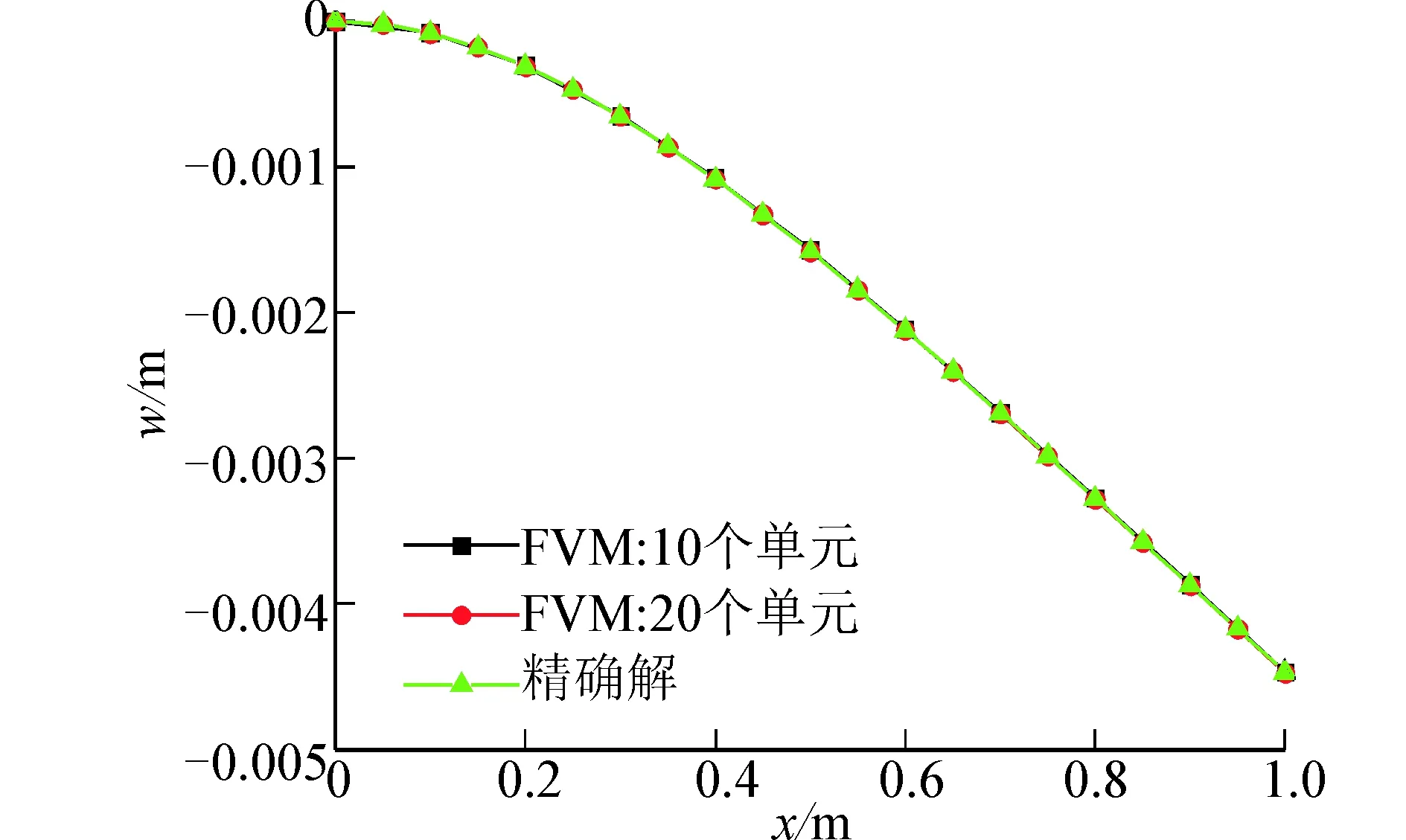
(b) L/H=50

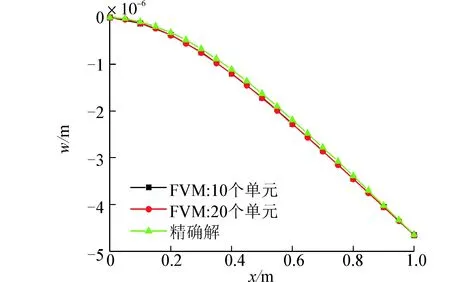
(c) L/H=5圖5 懸臂梁受均布載荷撓度曲線Fig. 5 The deflection curve for different L/H cantilever beams under uniform load

通過計算3種跨高比懸臂梁的撓度，從結(jié)果可以看出隨著離散控制體數(shù)的增加用有限體積法計算的結(jié)果趨近于精確解，并且當跨高比大于100時Timoshenko梁模型不存在剪切自鎖現(xiàn)象。

3.2 簡支梁受均布載荷靜力分析

均布載荷q=1 000 N/m;梁長L=1 m;梁寬T=0.02 m;梁高為H;剪切修正系數(shù)Ks=0.833; 楊氏模量E=210 GPa;泊松比為0.3;鐵木辛柯梁模型精確解：

(13)

式中：α為剪切修正系數(shù)，具體推導見文獻[11]。

圖6 簡支梁示意圖
Fig. 6 Sketch of simply-supported beam

計算了3種跨高比的撓度以及與精確解的誤差：首先選擇梁截面高度為0.2m，寬度為0.02m，跨高比為5，計算結(jié)果如圖7(a)，其次選擇梁截面高度為0.02m，寬度為0.02m，跨高比為50，計算結(jié)果如圖7(b)，最后選擇梁截面高度為0.008m，寬度為0.02m，跨高比為125，計算結(jié)果如圖7(c)。

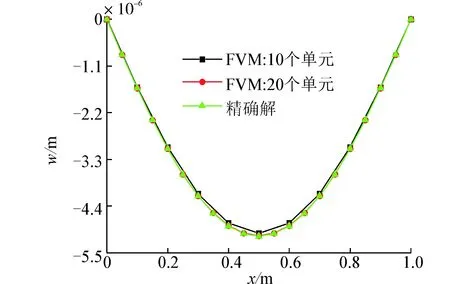
(a) L/H=5

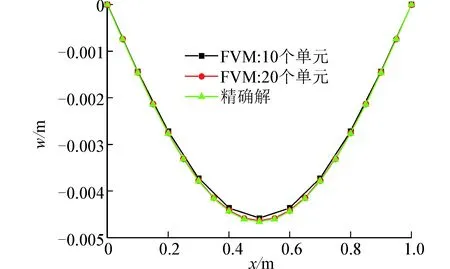
(b) L/H=50

(c) L/H=125圖7 簡支梁受均布載荷撓度曲線Fig. 7 The deflection curve for different L/Hsimply-supported beams under uniform load

將上述3種跨高比的數(shù)值結(jié)果進行誤差分析，其誤差如圖8所示:

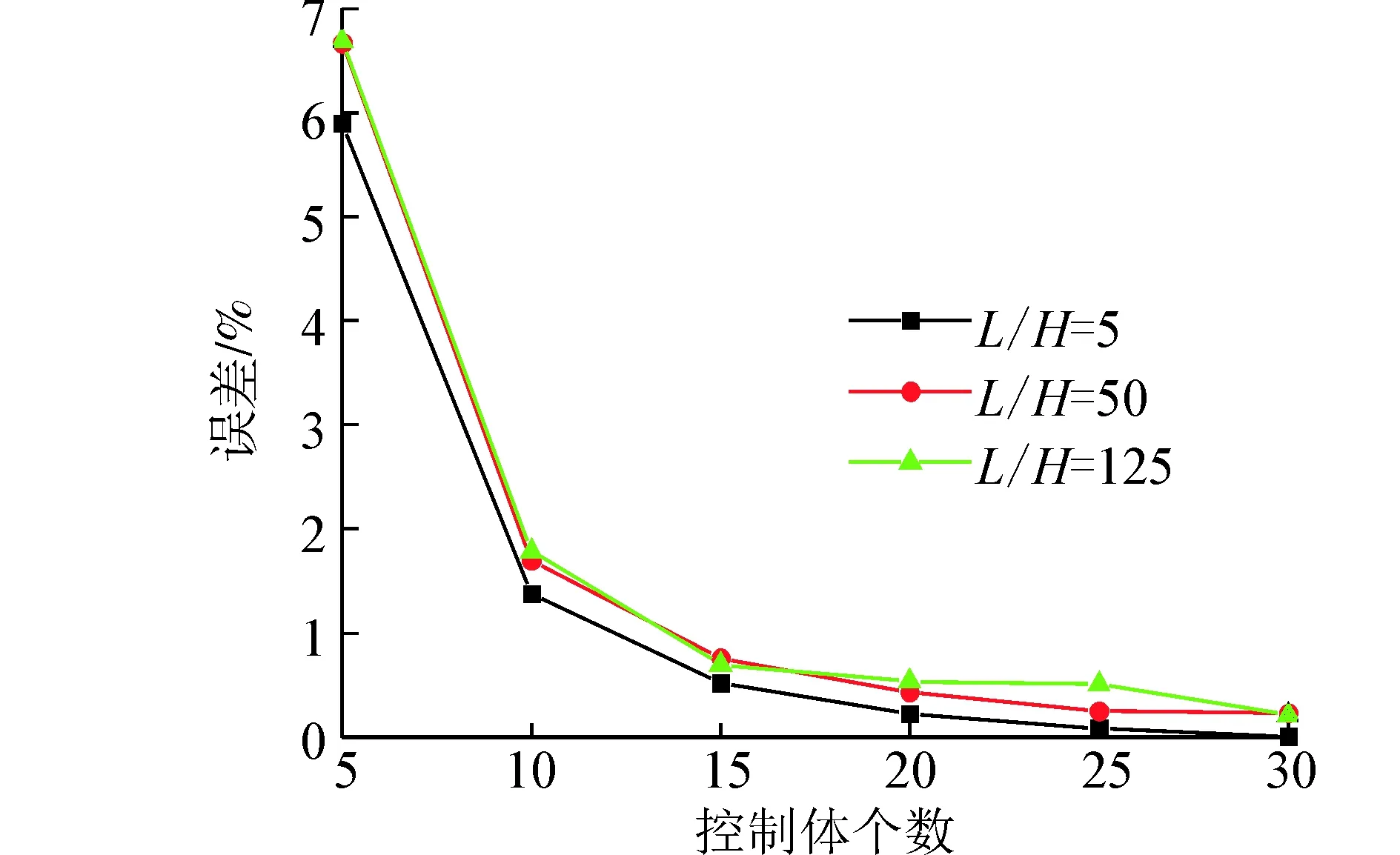
圖8 不同跨高比數(shù)值解與精確解的誤差Fig. 8 Error in the numerical and exact solution in different length-height ratios

此算例計算了3種跨高比簡支梁的撓度并與精確解進行了對比和相對誤差的計算，通過分析可知此方法對于不同跨高比的簡支梁同樣能夠較精確的描述并且隨著離散控制體的增加其得到的數(shù)值解與精確解的誤差在逐漸降低，與此同時當跨高比大于100時不存在剪切自鎖現(xiàn)象,進而也驗證了有限體積法可以應(yīng)用于梁的靜力分析。

3.3 簡支梁固有頻率的提取

簡支梁如圖6所示，梁長度為1m;材料密度為7 800kg/m3；材料泊松比為0.3。固有頻率精確解[11]為

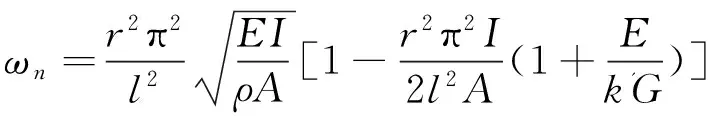
r=1，2,3...

(14)

計算了兩種跨高比簡支梁的固有頻率，分別對有限體積法及有限元法進行了誤差分析：首先用有限體積法和有限元法分別計算了截面高度為0.01m、寬度為0.01m，即跨高比為100的簡支梁的前三階固有頻率，并與精確解進行了對比如圖9(a)，其次用有限體積法和有限元法分別計算了截面高度為0.1m，寬度為0.01m即跨高比為10的簡支梁的前三階固有頻率，并與精確解進行了對比如圖9(b)。

(a) L/H=100

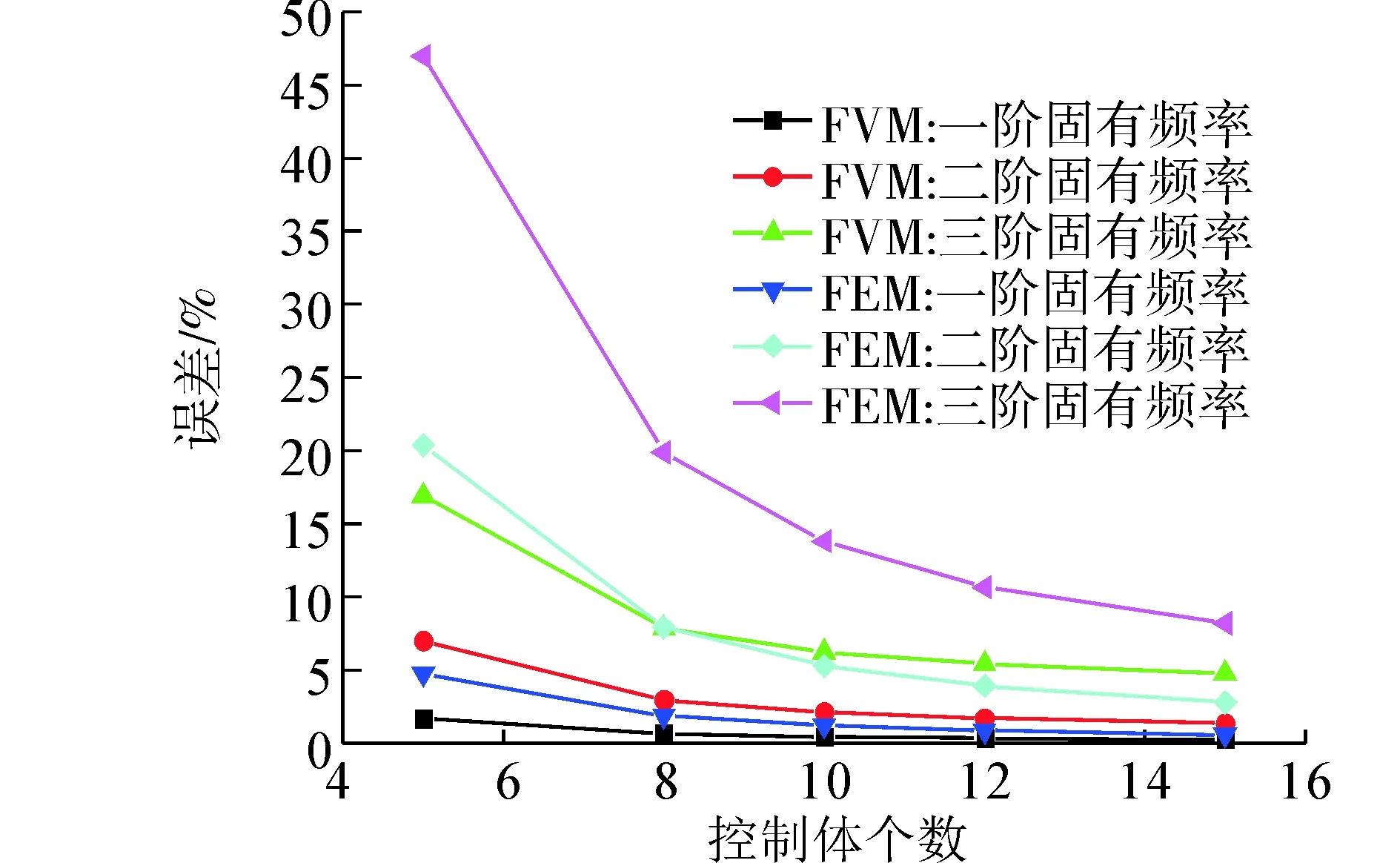
(b) L/H=10圖9 簡支梁前三階固有頻率誤差分析Fig. 9 Error analysis of first, second and third natural frequencies for simply-supported beam

此算例計算了2種高跨比梁的前三階固有頻率，通過以上兩圖對比可以看出隨著控制體數(shù)的增加固有頻率與精確解的誤差是越來越小的，與此同時在相同離散單元的情況下，對于前三階固有頻率的提取有限體積法的精度要比有限元的精度高。并且利用有限體積法得到的一階固有頻率與精確解之間的誤差最小，因此用有限體積法離散并用相應(yīng)提取特征值技術(shù)進行計算所得到的固有頻率是相對準確的，進而驗證了有限體積法可以應(yīng)用于Timoshenko梁模型固有頻率的提取。

3.4 簡支梁動力響應(yīng)分析

3.4.1 算例1

簡支梁如圖6所示，所承受載荷為Q，其隨時間分布如圖10所示;材料密度為7 800 kg/m3；泊松比為0.3；楊氏模量為210 GPa；剪切修正系數(shù)取0.833,選取的時間步長為10-6s，計算3種不同跨高比的梁中點響應(yīng)。

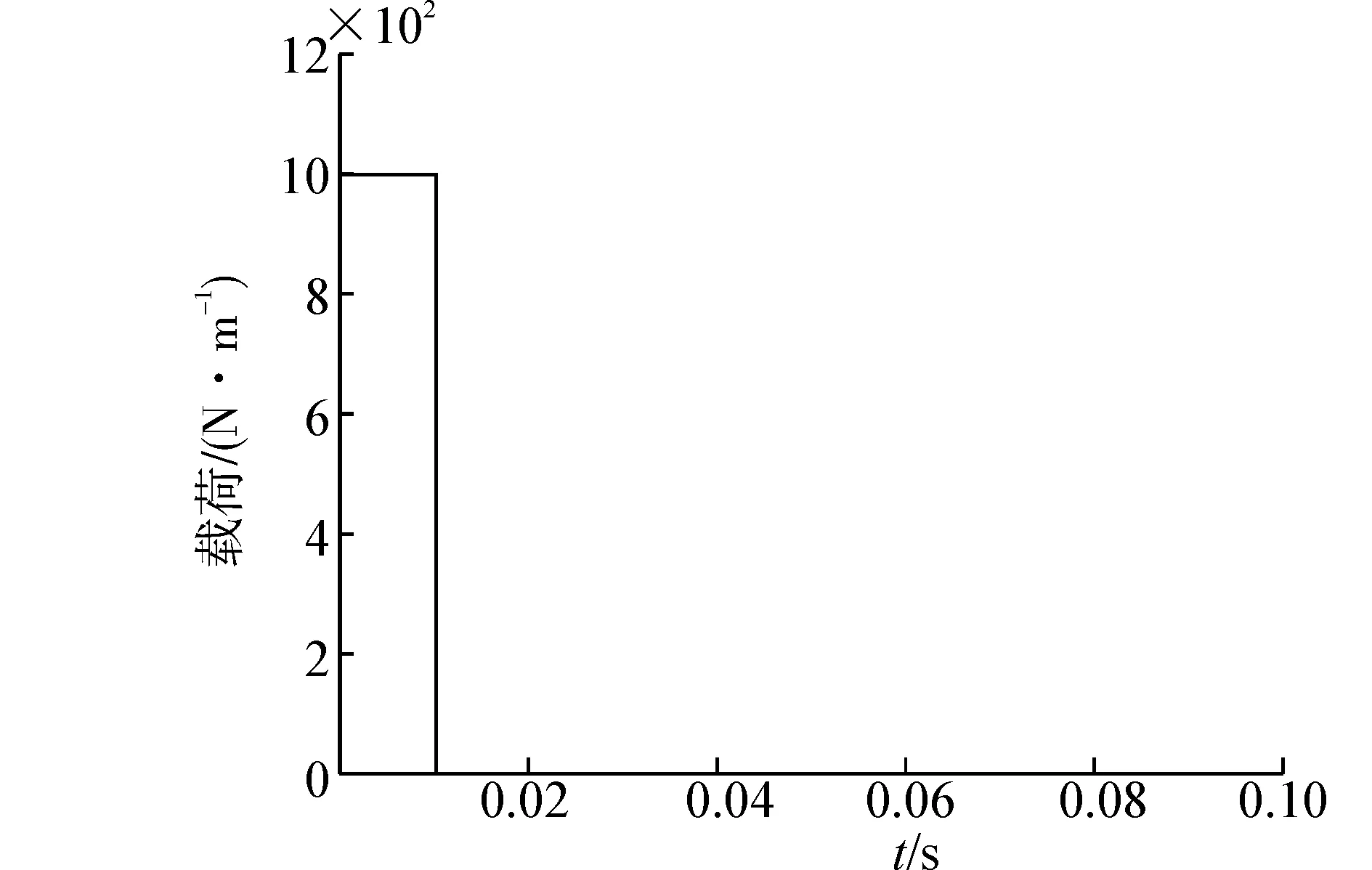
圖10 載荷隨時間分布圖(均布載荷)Fig. 10 Load-time curve(uniform load)

根據(jù)此載荷分布則解析解[12]：

當t<0.001s時，

(i=1,2,3,4)

(15)

當t>0.001 s時，

(i=1,2,3,4)

(16)

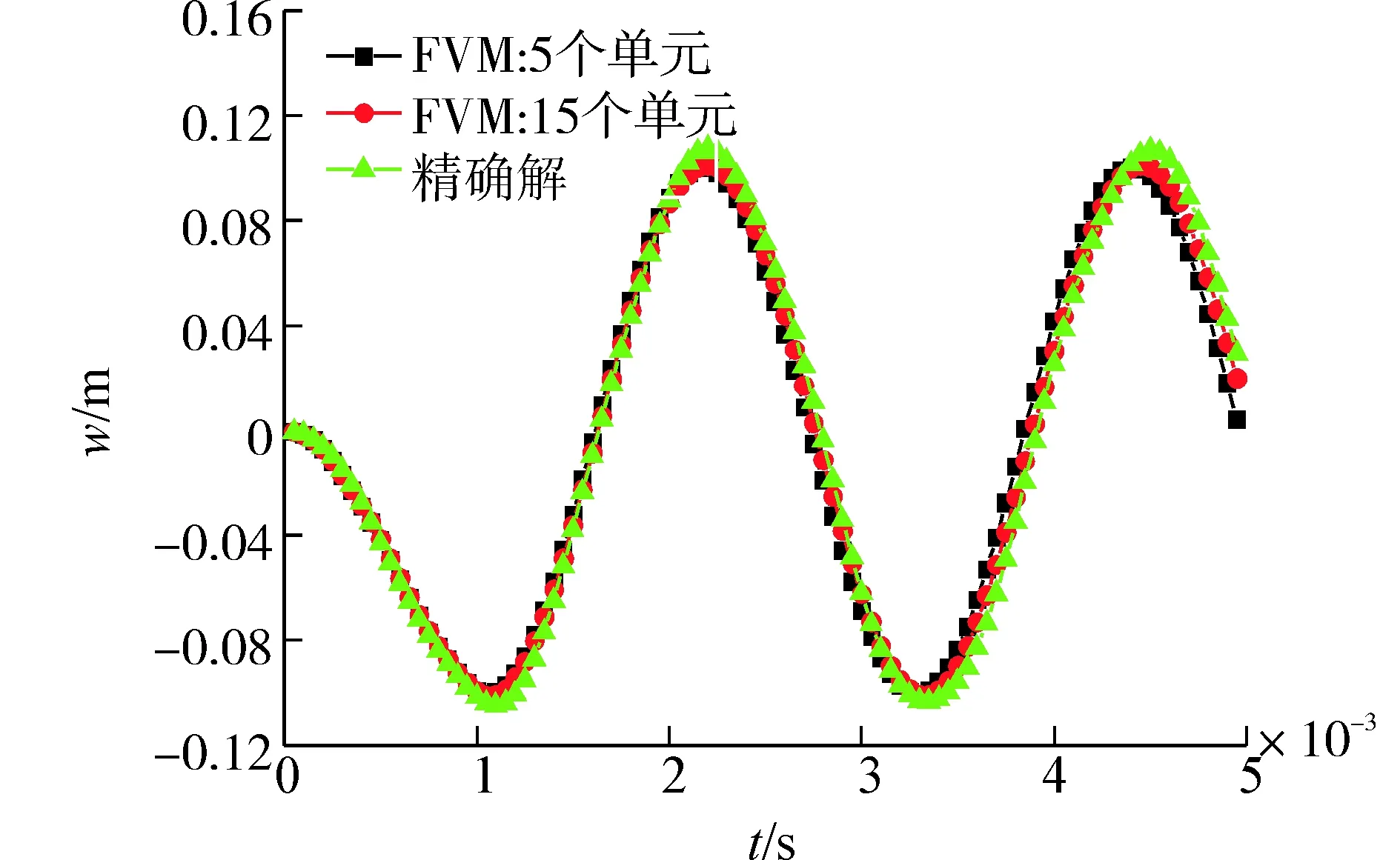
(a) L/H=5

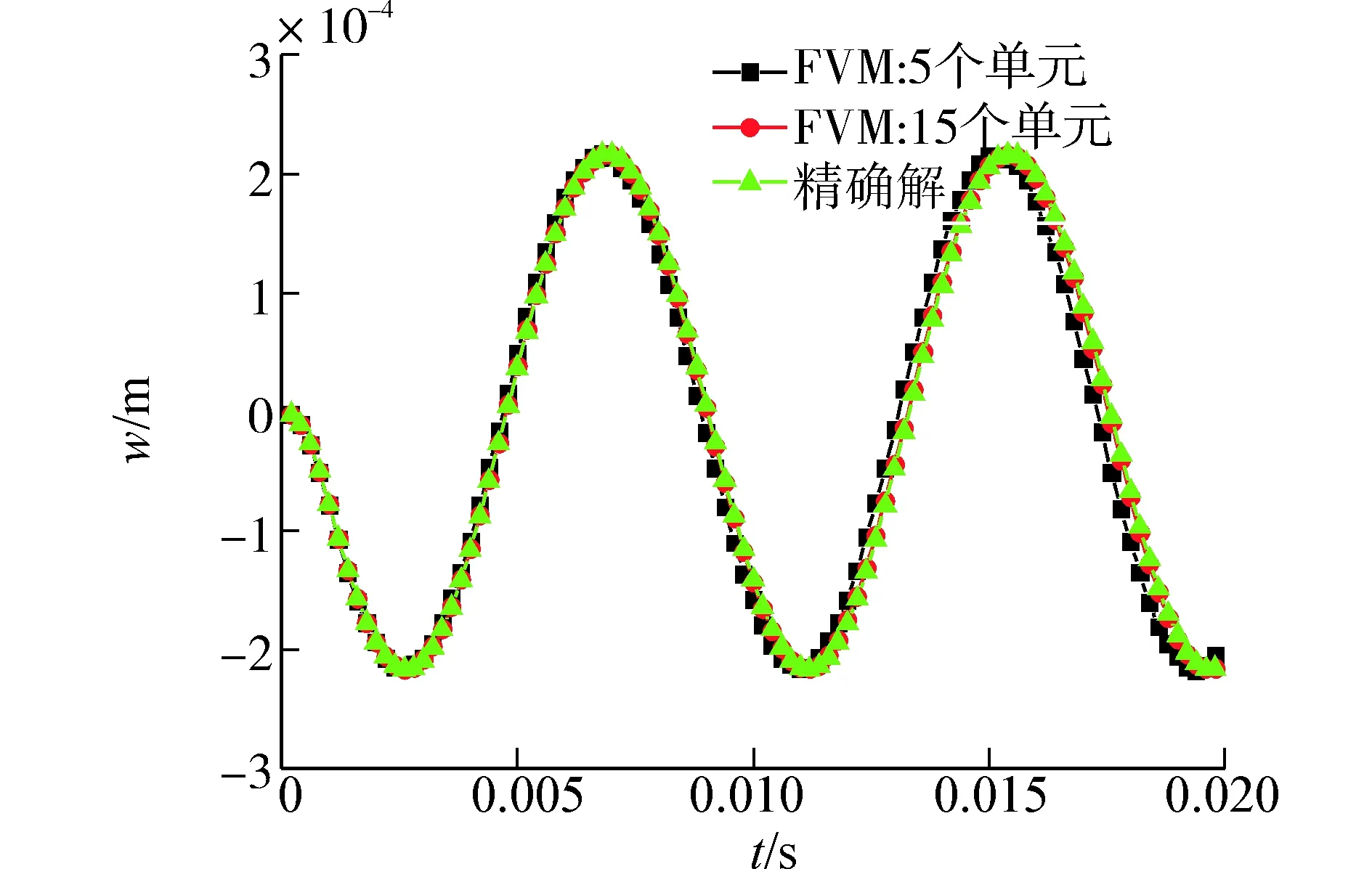
(b) L/H=20

(c) L/H=100圖11 簡支梁受均布載荷位移響應(yīng)曲線Fig. 11 Displacement-time curve for simply-supported beam under uniform load

首先計算了截面高度為0.2 m、寬度為0.01 m即跨高比為5，載荷分布如圖10，0.005 s的梁中點位移響應(yīng)，結(jié)果如圖11(a)，然后計算了截面高度為0.05 m、寬度為0.02 m即跨高比為20，載荷分布如圖10，0.02 s的梁中點位移響應(yīng)，結(jié)果如圖11(b)，最后計算了截面高度為0.01 m、寬度為0.02 m即跨高比為100，載荷分布如圖10，0.02 s的梁中點位移響應(yīng)，結(jié)果如圖11(c)。

此算例計算了3種跨高比簡支梁受均勻分布力的動力響應(yīng)，從圖中可以看出隨著控制體數(shù)的增加響應(yīng)曲線趨近于精確解并且當跨高比為100時不存在剪切自鎖現(xiàn)象，進而驗證了有限體積法可以應(yīng)用于Timoshenko梁模型的動力學分析。

3.4.2 算例2

一簡支梁的截面寬度為T;所承受載荷為F1和F2，作用的位置和載荷大小如圖12、13所示;材料密度為7 800kg/m3，泊松比為0.3，楊氏模量為210GPa，剪切修正系數(shù)為0.833,選取的時間步長10-6s，計算梁中點響應(yīng)。

圖12 載荷作用位置示意圖Fig. 12 Sketch of pined-pined beam under two concentrated forces

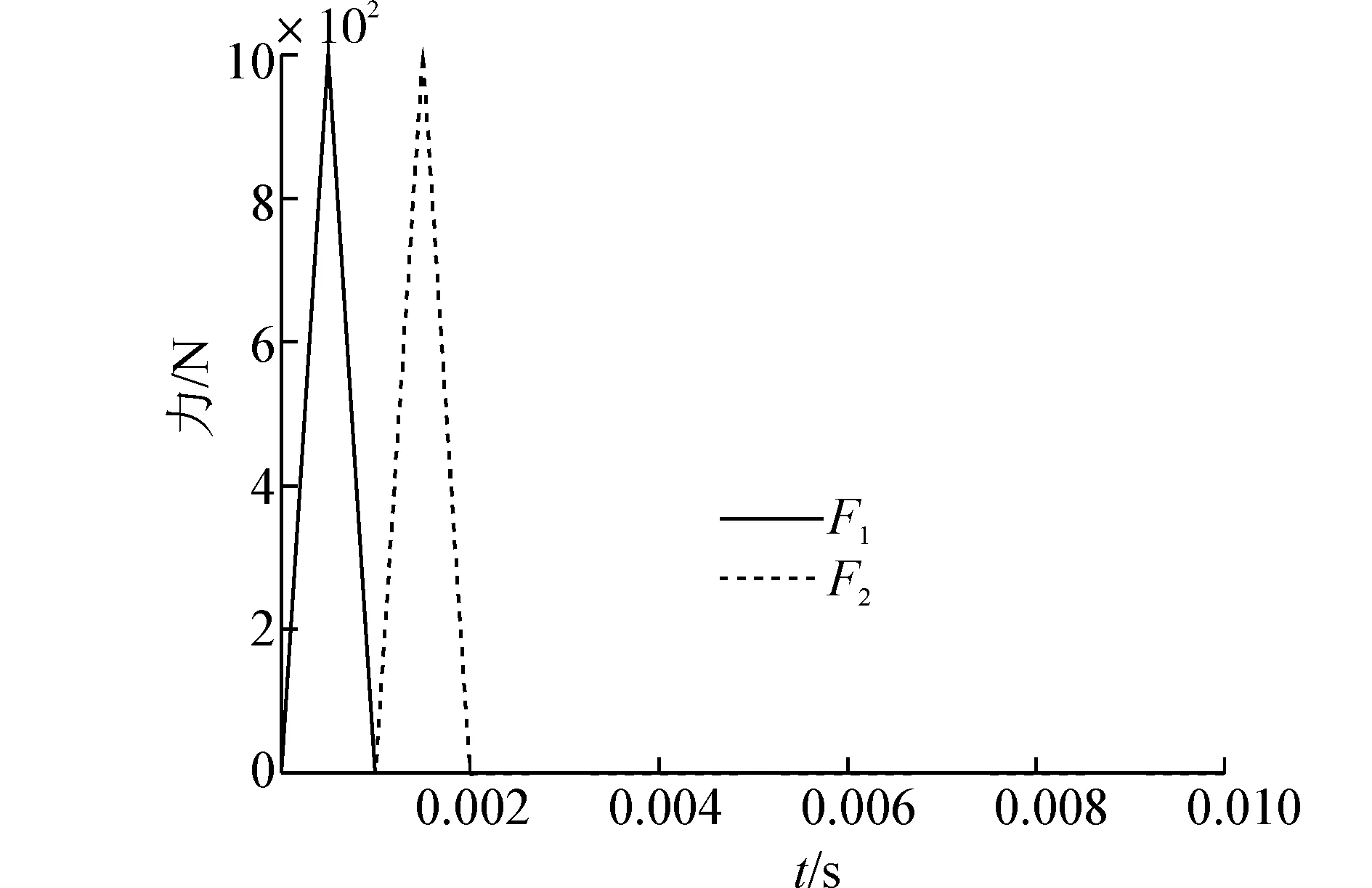
圖13 載荷-時間曲線(集中載荷)Fig. 13 Load-time curve(concentrate load)

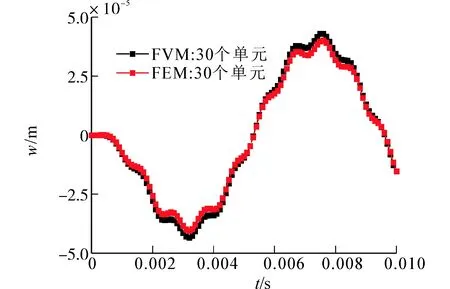
首先分別利用有限元法和有限體積法計算了梁截面高度為0.2m、寬度為0.1m即跨高比為5, 0.01s的梁中點位移響應(yīng)，結(jié)果如圖14(a)所示。然后計算了梁截面高度為0.05m、寬度為0.1m即跨高比為20, 0.01s的梁中點位移響應(yīng)，結(jié)果如圖14(b)所示。最后計算了梁截面高度為0.01m、寬度為0.1m即跨高比為100, 0.05s的梁中點位移響應(yīng)，結(jié)果如圖14(c)所示。

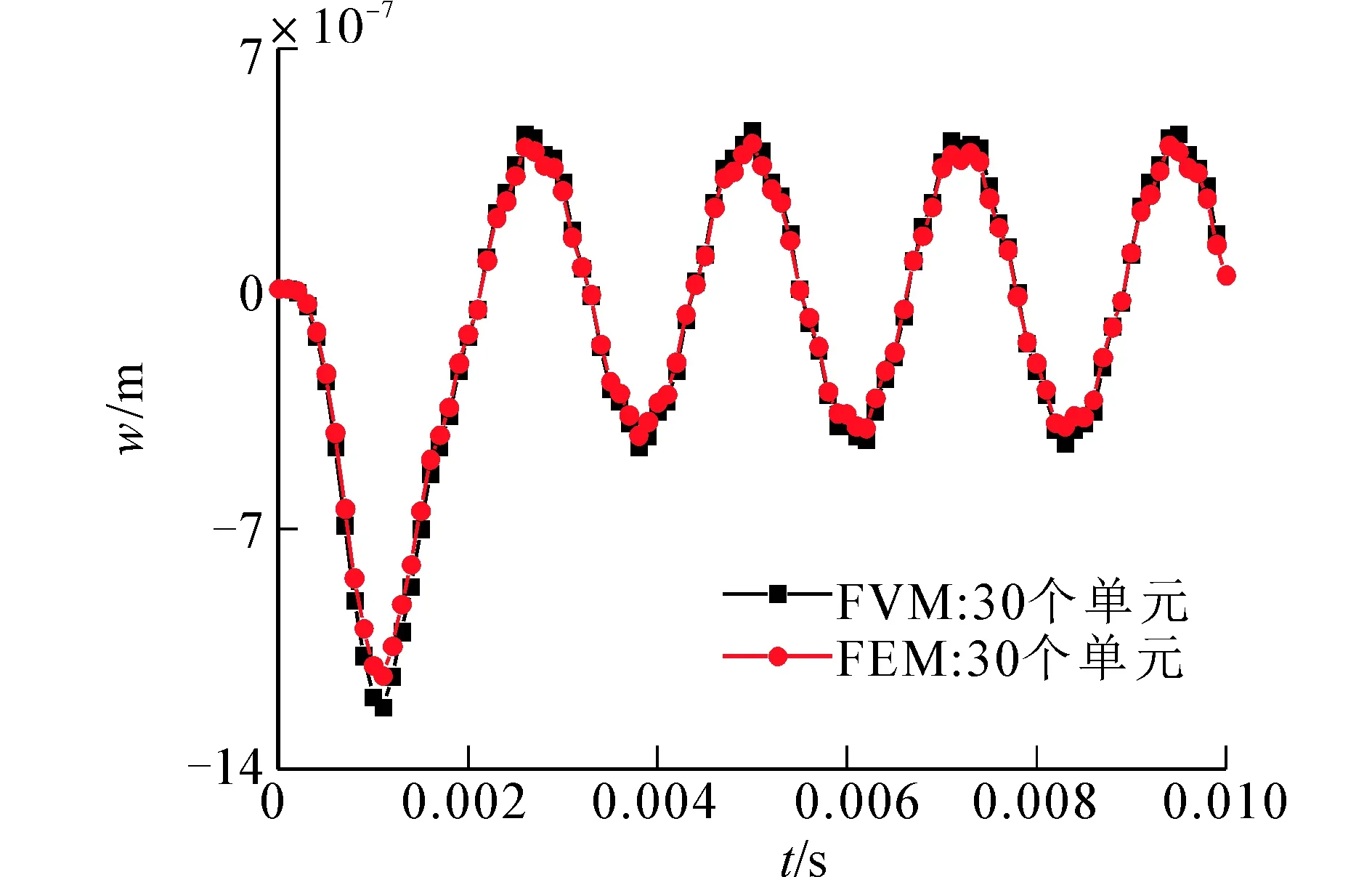
(a) L/H=5

(b) L/H=20

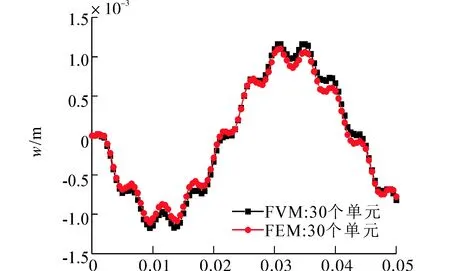
(c) L/H=100圖14 簡支梁受集中載荷位移響應(yīng)曲線Fig. 14 Displacement-time curve for simply-supported beam under concentrate load

此算例計算了3種跨高比簡支梁受不同相位多激勵的動力響應(yīng)，通過與有限元軟件計算結(jié)果比較，可以發(fā)現(xiàn)在相同離散單元下，有限體積法可以相對準確預(yù)測梁受不同相位多激勵響應(yīng)，并且同時適應(yīng)于細長梁和深梁，不存在剪切自鎖現(xiàn)象。

4 結(jié)論

通過以上4個算例可以得到如下結(jié)論:

1)有限體積法可應(yīng)用于不同跨高比的梁并且不存在有限元中Timoshenko梁模型的剪切自鎖現(xiàn)象，即可以利用有限體積法對不同跨高比的梁只用一種模型即可得到相對準確數(shù)值解。

2)驗證了有限體積法可以應(yīng)用Timoshenko梁模型對梁進行靜力分析，特征值和動力響應(yīng)分析，并且其數(shù)值結(jié)果與精確解和有限元解吻合較好。

3)利用有限體積法可以預(yù)測梁受均布載荷以及不同相位多激勵的梁的響應(yīng)。

[1]包剛強, WANG Erke, 郝清亮, 等. 對主流有限元軟件控制剪切自鎖和沙漏模式的比較和研究[C]//第八屆中國CAE工程分析技術(shù)年會暨2012全國計算機輔助工程(CAE)技術(shù)與應(yīng)用高級研討會論文集. 成都, 2012: 8.

[2]MACDONALD P W. The computation of transonic flow through two-dimensional gas turbine cascades[D]. ASME, 1971: 71-89.

[3]MACCORMACK R W, PAULLAY A J. Computational efficiency achieved by time splitting of finite difference operators[D]. San Diego:AIAA, 1972: 72-154.

[4]RIZZI A W, INOUYE M. Time-split finite-volume method for three-dimensional blunt-body flow[J]. AIAA Journal, 1973, 11(11): 1478-1485.

[5]PATANKAR S V. Numerical heat transfer and fluid flow, series in computational methods in mechanics and thermal sciences[M]. Washington, DC: CRC Press, 1980: 5-20.

[6]HIRSCH C. Numerical computation of internal and external flow, Vol. I[M]. Chichester: Wiley, 1988: 17-38.

[7]WHEEL M A. A finite volume method for analysing the bending deformation of thick and thin plates[J]. Computer Methods in Applied Mechanics and Engineering, 1997, 147(1/2): 199-208.

[8]FALLAH N, HATAMI F. A displacement formulation based on finite volume method for analysis of Timoshenko beam[C]//Proceedings of the 7th International Conference on Civil Engineering. Tehran, Iran, 2006.

[9]BATHE K J. Finite element procedures[M]. New Jersey: Prentice Hall, 1996: 770-774.

[10]鐵摩辛柯 S. 材料力學[M]. 北京: 科學出版社, 1978: 210-216.

[11]COWPER G R. The shear coefficient in Timoshenko’s beam theory[J]. Journal of Applied Mechanics, 1966, 33(2): 335-340.

[12]張義民. 機械振動[M]. 北京: 清華大學出版社, 2007: 187-198.

Static and dynamic analysis of Timoshenko beam model based on the finite volume method

JING Lilong, ZHANG Wenping, MING Pingjian, FU Lirong, LIU Xiaogang

(College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China)

In order to explore a numerical simulation method based on the Timoshenko beam model, a study was done on beam numerical simulation using the Timoshenko beam model, based on the finite volume method (FVM). In order to examine the beam's shear deformation, the beam model was discretized by FVM, and static and dynamic analyses were conducted. After first calculating some typical examples, the derived numerical results and the analytic solutions with FVM, a comparison was made with the solution by FVM. It is shown that FVM provides high precision analysis, with no shear-locking phenomenon for thin and long beams when discretizing Timoshenko beam based on FVM. This validates FVM for analyzing Timoshenko beam static bending, inherent characteristics, and dynamic response problems.

finite volume method; Timoshenko beam; static analysis; dynamic analysis; shear locking phenomenon; natural frequency; displacement response

2014-08-28.

時間：2015-07-15.

中央高校基本科研業(yè)務(wù)費專項資金資助項目(HEUCF130302).

井麗龍(1987-), 男, 博士研究生; 張文平(1956-)，男，教授，博士生導師； 明平劍(1980-), 男, 副教授.

明平劍, E-mail: pingjianming@hrbeu.edu.cn.

10.3969/jheu.201408044

TK124

A

1006-7043(2015)09-1217-07

網(wǎng)絡(luò)出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20150715.1728.008.html