改進的多端元高光譜解混算法

趙春暉, 崔士玲, 趙艮平

(哈爾濱工程大學(xué) 信息與通信工程學(xué)院，黑龍江 哈爾濱 150001)

改進的多端元高光譜解混算法

趙春暉, 崔士玲, 趙艮平

(哈爾濱工程大學(xué) 信息與通信工程學(xué)院，黑龍江 哈爾濱 150001)

針對經(jīng)典多端元光譜混合模型(MESMA)存在著計算量大，端元預(yù)選繁瑣以及過擬合等缺點，提出了一種改進的多端元解混算法。該算法根據(jù)正交子空間投影具有分離感興趣信號與不感興趣信號的特點，將像元投影到全部地物端元(每類地物選擇一條類內(nèi)光譜)構(gòu)成的正交子空間上，按照投影值確定構(gòu)成混合像元每類地物的類內(nèi)光譜，在下一步迭代求解的過程中，分離出已確定地物類內(nèi)光譜的像元，降低計算量，然后根據(jù)重構(gòu)誤差變化量確定最優(yōu)端元個數(shù)，避免過擬合。實驗結(jié)果表明，改進的算法反演豐度誤差和解混時間都比原有算法降低很多。

高光譜；多端元；光譜解混；正交子空間投影；誤差變化量；類內(nèi)光譜變化

近年來，高光譜遙感技術(shù)快速發(fā)展，已經(jīng)在農(nóng)業(yè)生產(chǎn)、環(huán)境監(jiān)測、地質(zhì)勘探、軍事對抗等多個領(lǐng)域得到成功應(yīng)用。由于地面的復(fù)雜多樣性及傳感器空間分辨率的限制，使得高光譜圖像普遍存在著混合像元的情況，混合像元的存在嚴重影響后續(xù)圖像處理的精度[1-2]。

傳統(tǒng)光譜混合模型一個類別用一個固定的光譜端元來代表，由于高光譜圖像空間幅度大導(dǎo)致每類地物內(nèi)的光譜變化一般很大，在這種條件下固定端元光譜很難準確刻畫一個類別，導(dǎo)致解混精度不高[3]。Roberts D 等提出多端元光譜混合模型(MESMA)[4]，Asner G 等應(yīng)用蒙特卡羅來估計豐度值及其信度區(qū)間來克服光譜變化(AutoMCU)[5]， B. Somers 根據(jù)類內(nèi)類間光譜變化，提出穩(wěn)定區(qū)域解混(SZU)[6]算法，解混效果較好，但是參數(shù)的變化對解混精度影響很大。歸一化光譜混合模型 (NSMA)以及基于導(dǎo)數(shù)的光譜解混算法(DSU)，這兩者物理意義不夠明確。其中 MESMA 算法是至今應(yīng)用最為廣泛的一種多端元光譜解混算法[7]，但是其計算量大，端元預(yù)選繁瑣，而且采用重構(gòu)誤差最小判斷最優(yōu)端元組合，會導(dǎo)致過擬合現(xiàn)象，解混時的采用的端元個數(shù)要比真實構(gòu)成混合像元端元個數(shù)大。針對上述問題，本文提出了一種改進的多端元解混算法，有效地解決了這一難題。

1 傳統(tǒng)線性光譜混合模型

傳統(tǒng)線性光譜混合模型[8]可以表示為：

(1)

式中：x為觀測向量，ej是端元，aj是混合系數(shù)，M是端元的數(shù)量，N代表噪聲影響。

該模型有兩個約束條件：

1)aj≥0非負約束；

由最小二乘算法反演豐度，如式(2)，每個像元由所有的端元E反演，然后重構(gòu)像元如式(3)。

(2)

(3)

在傳統(tǒng)線性光譜混合模型中，一個類別用一個固定的光譜端元E來代表。然而，高光譜圖像空間幅度大導(dǎo)致了類內(nèi)光譜變化一般很大，在這種條件下一個端元光譜很難準確刻畫一個類別，導(dǎo)致光譜解混精度不高，改進多端元光譜混合模型算法可以很好地解決這個問題。

2 正交子空間投影算法

對于傳統(tǒng)線性光譜混合模型，觀測向量x可以表示成感興趣部分與不感興趣部分的混合[9]，再疊加上噪聲，如下：

x=dαp+Uγ+N

(4)

式中：d為感興趣部分，αp為d所對應(yīng)的豐度，U為不感興趣部分，γ為U所對應(yīng)的豐度，N為噪聲。

(5)

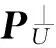
(6)

由式(6)可以看出，經(jīng)過將觀測信號投影到非感興趣正交子空間上，背景信號被消除，原始噪聲也得到了投影壓縮。

3 改進MESMA算法

傳統(tǒng)線性光譜混合模型端元矩陣E是固定不變的，然而，實際上不同像元包含的端元類別與端元個數(shù)是不同的，如果采用固定的端元解混，反演的豐度是不準確的，顯然多端元光譜解混模型更加合理。

線性多端元光譜混合模型如下：

(7)

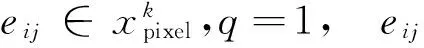
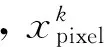
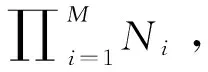
為了解決這個問題，采用均方根誤差變化量 △RMSE來判斷，如式(7)所示，如果 △RMSE小于設(shè)定的閾值，說明多出的這個端元對混合像元解混重構(gòu)誤差影響微弱，該端元不構(gòu)成該混合像元，于是選擇個數(shù)較小的端元組合解混相關(guān)的像元，反之選擇較大個數(shù)端元組合模型：

(8)

(9)

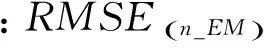
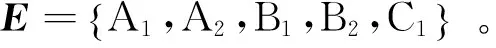
1)構(gòu)造 3-端元組合為：

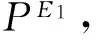
(10)

投影值為零的像元U1是由端元E1構(gòu)成的，分離出像元U1，以此類推，分別計算剩下的像元到端元E2、E3、E4的正交子空間投影得到投影值小于設(shè)定閾值的像元，得到結(jié)果表示為U2、U3、U4，這樣通過正交子空間投影逐步將像元U1、U2、U3、U4分離。

3)確定構(gòu)成像元U1、U2、U3、U4最優(yōu)端元個數(shù)。

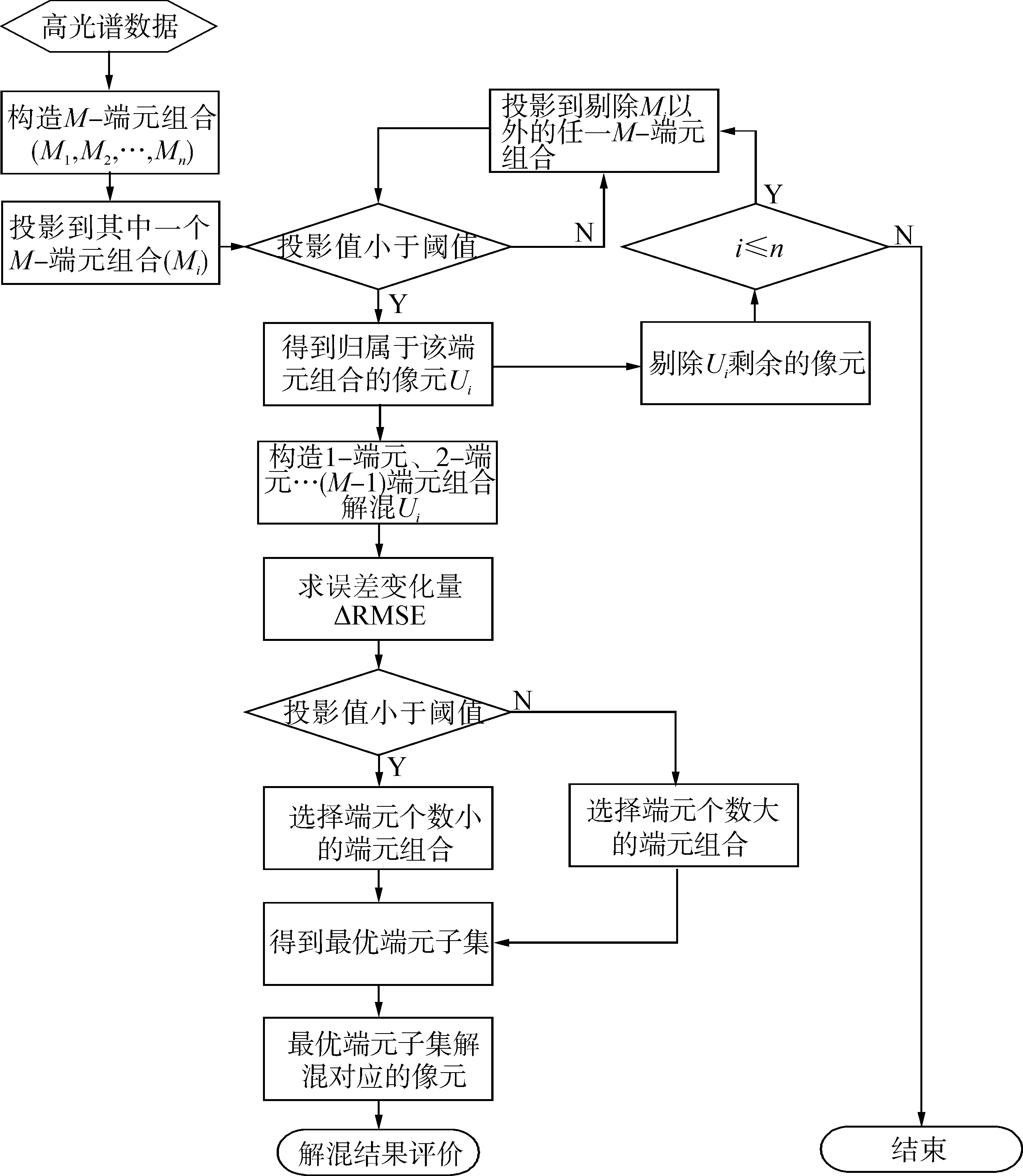
圖1 解混流程圖Fig. 1 Unmixing flow chart

4 仿真實驗

為了驗證改進算法的有效性，采用真實數(shù)據(jù)和模擬數(shù)據(jù)進行仿真實驗，并將改進的算法與另外3種算法進行對比。計算機的硬件配置為：處理器為IntelCorei3，主頻為 2.13GHz，內(nèi)存為DDR3 4GB，仿真軟件為MATLAB7.11 版本。

為了客觀地評價混合像元分解的精度，采用定性和定量兩種評價準標[10]。定性評價采用光譜解混分量圖：它是某類別成分在圖像各像元中所占比例的二維灰度顯示，每個類別對應(yīng)一幅解混分量圖。定量分析對于已知真實數(shù)據(jù)的精度評價采用反演豐度與參考值之間的均方根誤差RMSE為：

(11)

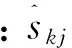
4.1 模擬數(shù)據(jù)實驗

從美國地質(zhì)調(diào)查局(USGS)礦物光譜庫選取 6 種礦物，分別為明礬石、高嶺石、蒙脫石、綠脫石、白云母和高嶺土，每類礦物選擇 5 條類內(nèi)光譜，用這 30 條光譜合成具有 5 000 個像元的具有 224 波段的高光譜數(shù)據(jù)，每個像元由 6 類礦物(每類礦物選擇一條光譜)中的若干種隨機混合而成，滿足豐度非負、和為一條件限制，為模擬真實的高光譜圖像，附加信噪比為 35dB的高斯白噪聲。

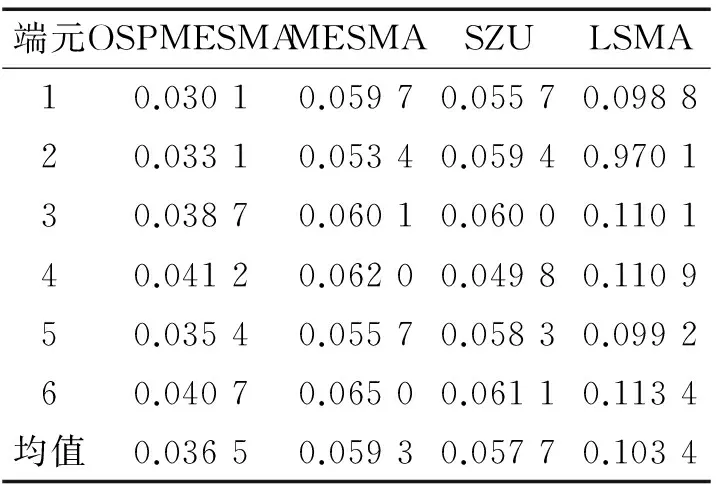
表1 解混豐度誤差對比

表1 是 6 種礦物反演豐度誤差對比，表中顯示改進算法反演豐度誤差均比其他3種算法低，并且前三者算法誤差都低于傳統(tǒng)固定端元解混算法，對于克服類內(nèi)光譜變化均起到了積極作用，同時說明改進算法的有效性。

4.2 真實高光譜數(shù)據(jù)實驗

實驗采用了美國航空可見光/紅外成像光譜儀所測美國印第安納州實驗田高光譜數(shù)據(jù)。圖像大小為 144×144，220 波段，將原始的 220 波段中受噪聲影響較大的一些波段去除后選取 200 波段作為仿真研究對象。從中選擇 3 類地物，干草，喬木，玉米，分別有 489、1294、834 樣本點，平均化后獲得3類代表光譜如圖 2 所示，其空間分布標號圖如圖 3(a) 所示。

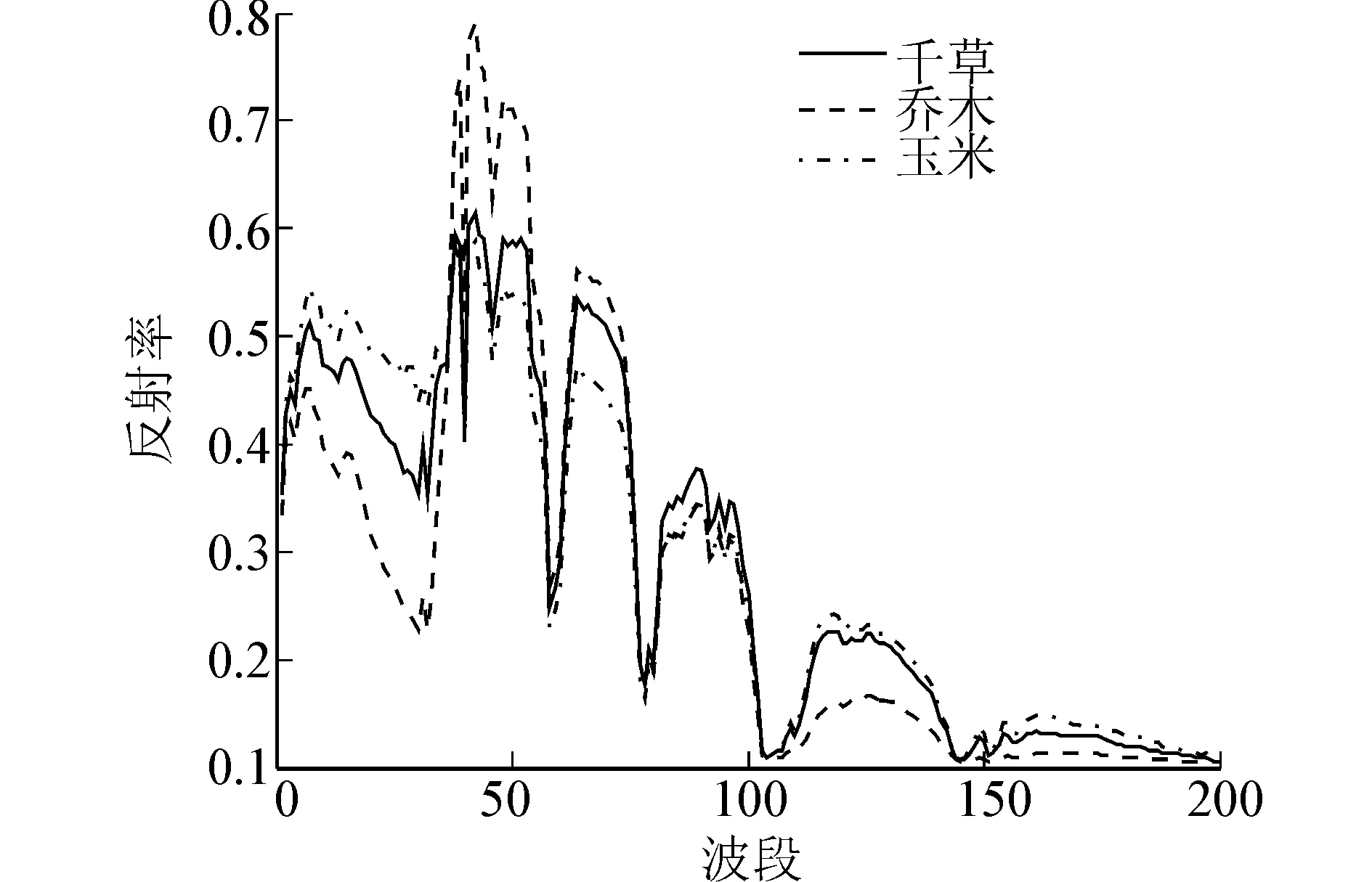
圖2 干草、喬木、玉米光譜曲線Fig. 2 Spectral curves of hong-windrowed woods and corn

(a) 真實地物分布標號圖

(b) OSPMESMA算法解混分量圖

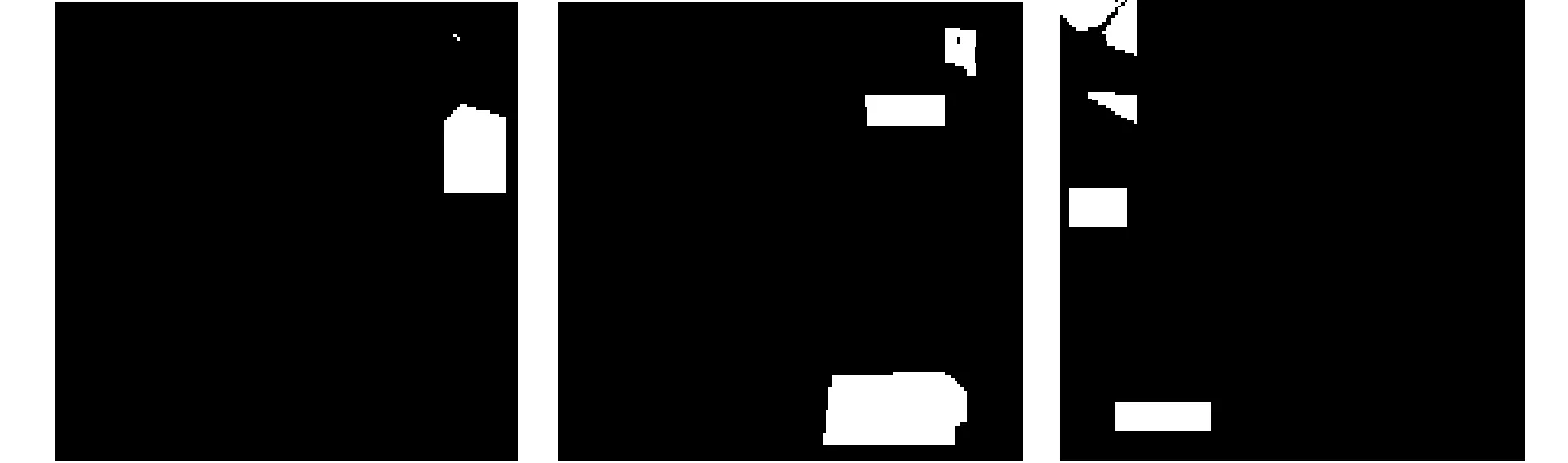
(c) MESMA算法解混分量圖

(d) SZU算法解混分量圖

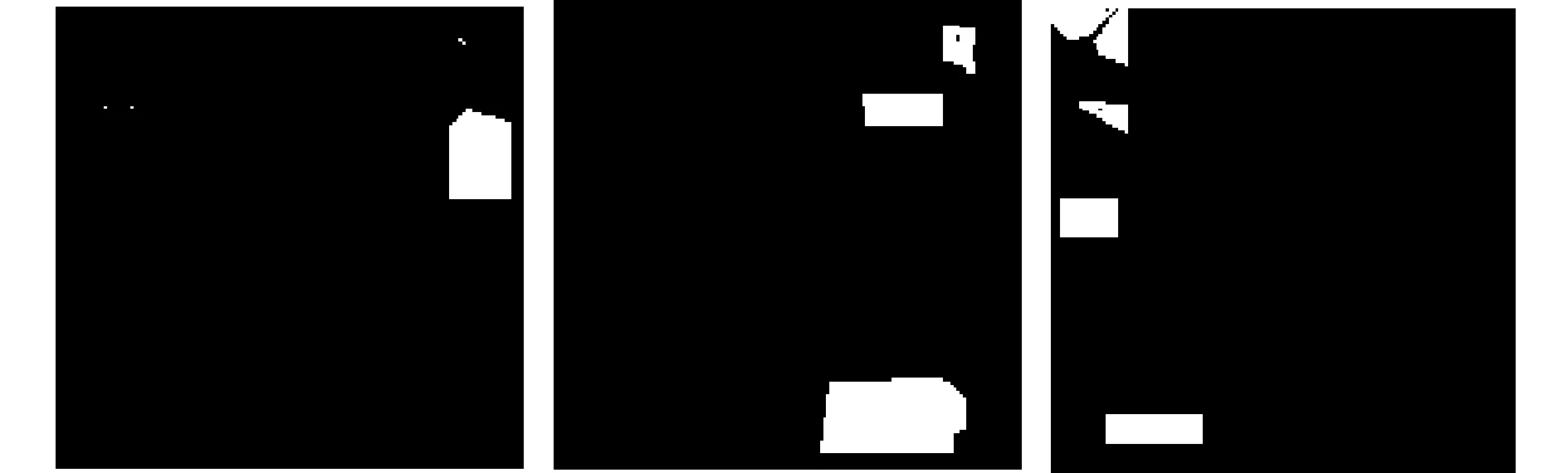
(e) LSMA算法解混分量圖圖3 3類地物解混分量圖對比Fig. 3 Unmixng component figures of three kinds of feature

表 2 是4種算法解混豐度均方根誤差對比，其中 OSPMESMA 和 MESMA 算法誤差是在 11 種端元組合條件下得到的結(jié)果。從中可以看到，OSPMESMA 算法誤差相對其他3種算法大大降低。在解混分量圖中，灰度越亮代表該類別在所對應(yīng)的混合像元中的豐度值越大，反之亦然。圖 3 是更直觀的表示，OSPMESMA 算法3類地物得到很好的體現(xiàn)，解混結(jié)果與真實地物分布十分接近，而其他3種算法解混結(jié)果較模糊，不能有效區(qū)分不同地物。其中 MESMA 和 SZU 算法不論解混誤差上，還是分量圖上，效果都比傳統(tǒng)固定端元解混效果優(yōu)良，它們在克服類內(nèi)光譜變化上均起到了積極作用，也說明多端元模型更加合理。

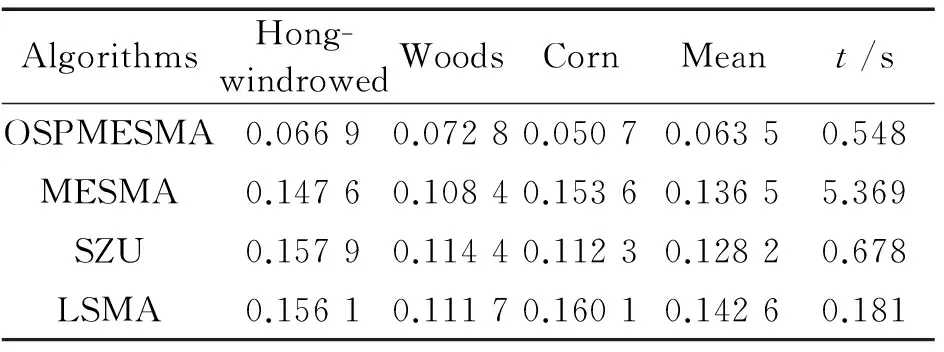
表2 解混豐度誤差對比

表 3 和表 4 是在類內(nèi)變化光譜增多的情況下，OSPMESMA 和 MESMA 算法解混豐度誤差和解混時間對比，由于 SZU 和 LSMA 算法解混用到的解混端元是固定的，解混結(jié)果和類內(nèi)變化光譜個數(shù)沒有關(guān)系，所以表中只列出了這兩者的結(jié)果。可以看到，隨著端元組合數(shù)的增大，OSPMESMA 算法解混誤差始終小于 MESMA 算法，時間也比后者短，精度和效率上都較優(yōu)良。

表3 解混豐度誤差隨端元組合數(shù)變化結(jié)果

Table 3 The change of abundance error with the number of endmember combinations

Endmembercombinations711151923OSPMESMA0.06360.06350.06320.06260.0621MESMA0.14220.13650.14140.13520.1342

表4 解混時間隨端元組合數(shù)變化結(jié)果

Table 4 The change of time with the number of endmember combinations

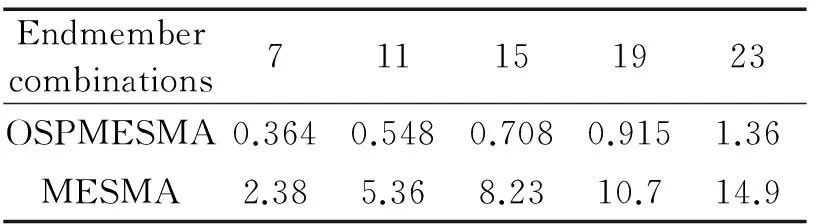
Endmembercombinations711151923OSPMESMA0.3640.5480.7080.9151.36MESMA2.385.368.2310.714.9

圖 4 和圖 5 是4種算法隨著端元組合數(shù)增大，解混豐度誤差和時間變化趨勢。SZU 和 LSMA 算法豐度誤差和時間始終保持不變，OSPMESMA 和 MESMA 算法豐度誤差呈下降趨勢，而解混時間逐次遞增，其中 OSPMESMA 算法兩者變化都比較緩慢，而 MESMA 算法解混時間相對于解混豐度誤差變化劇烈，解混時間急速上升。

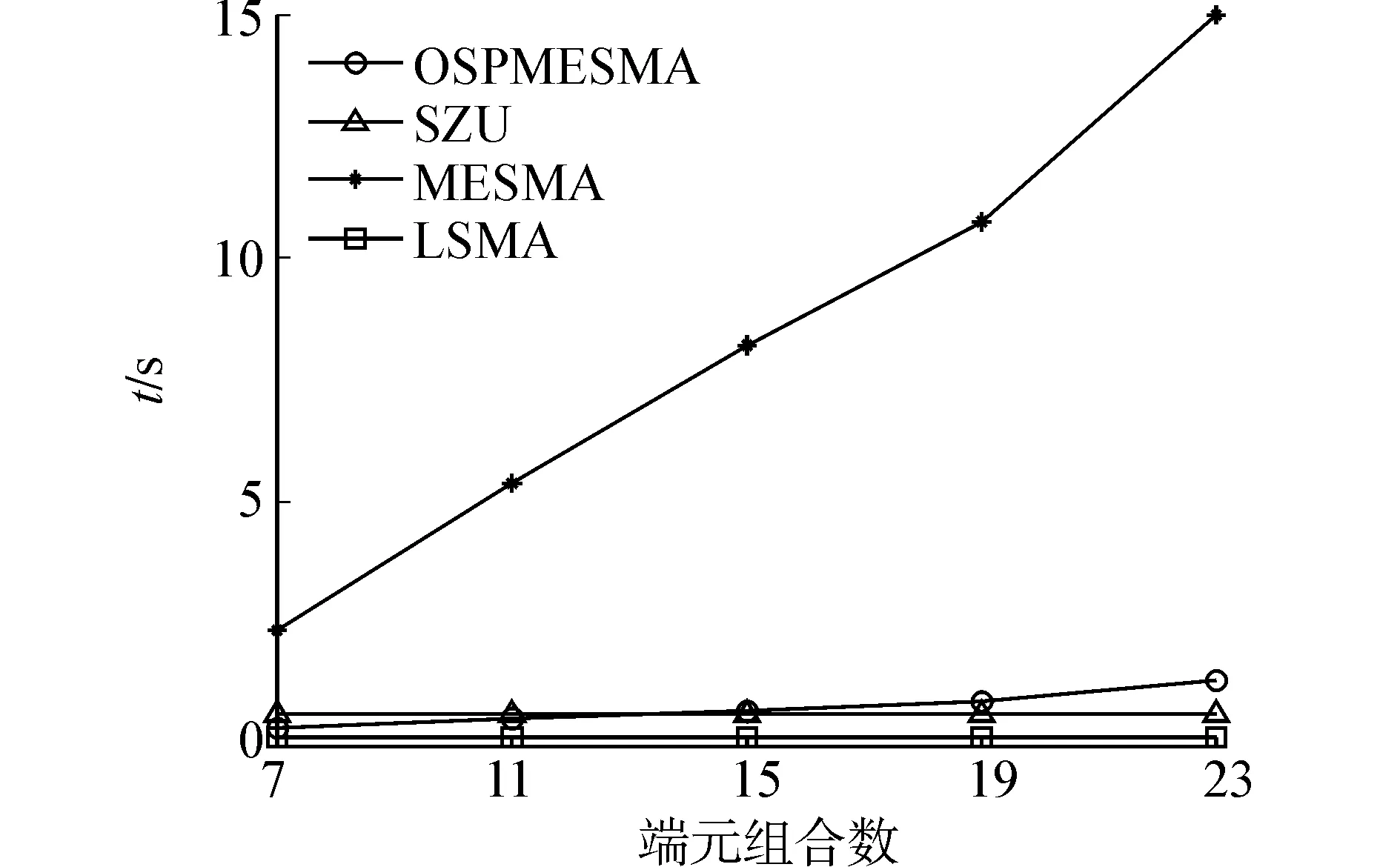
圖4 解混時間Fig. 4 Unmixing time

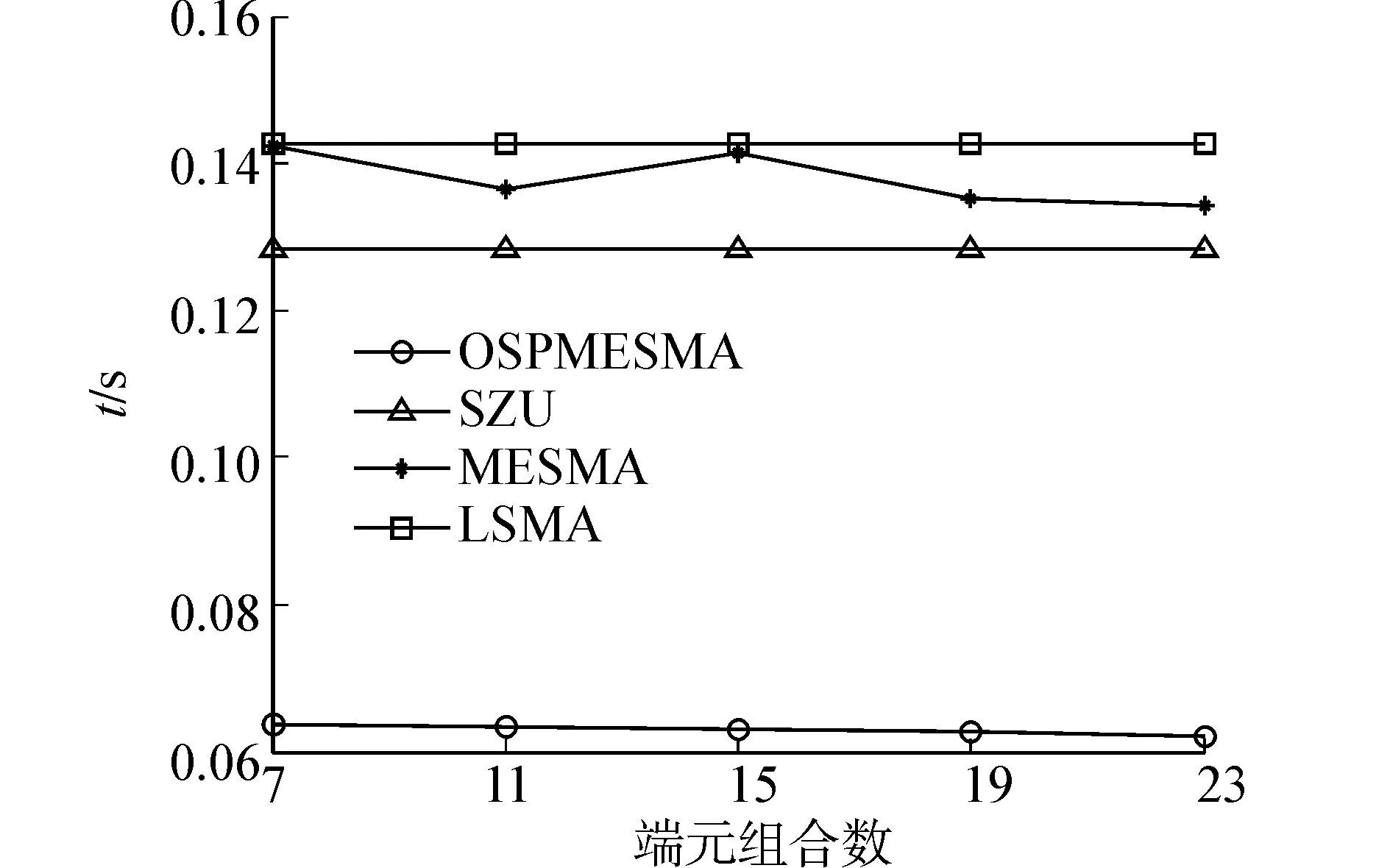
圖5 解混豐度誤差Fig. 5 Abundance error of unmxing

圖 6 是4種算法3種地物豐度誤差分布直方圖，直觀地看到，OSPMESMA 算法豐度誤差聚集在 0 值附近，誤差幾乎都落在 -0.2～0.2 之間，而其他3種算法誤差分布散落，落在 -0.2 和 0.2 以外的像元較多，可見改進的算法相對較好。

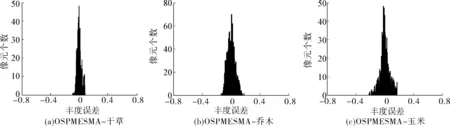
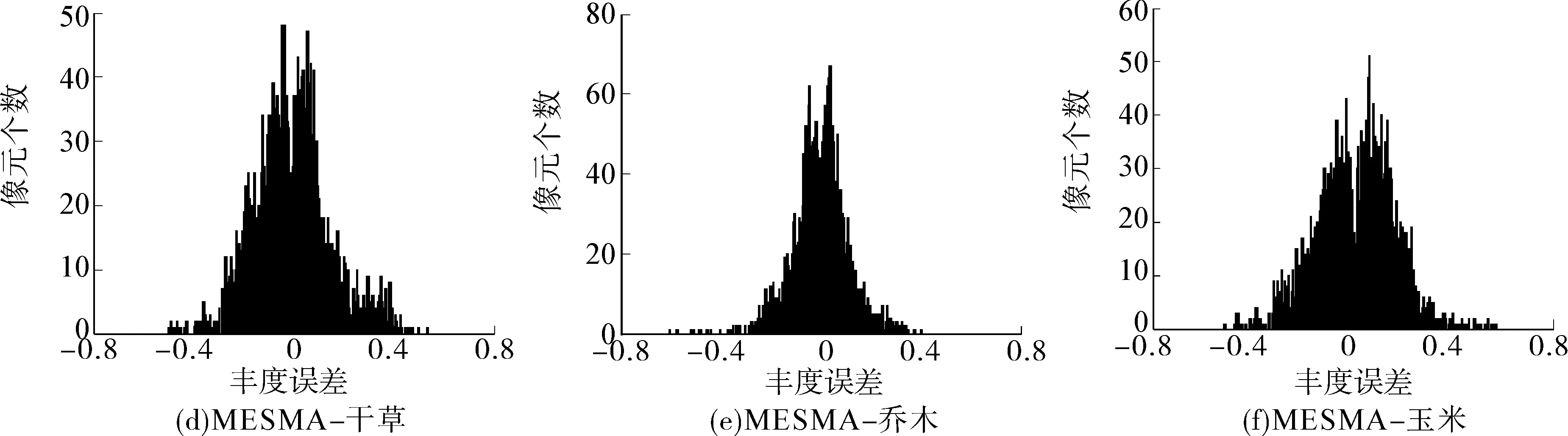
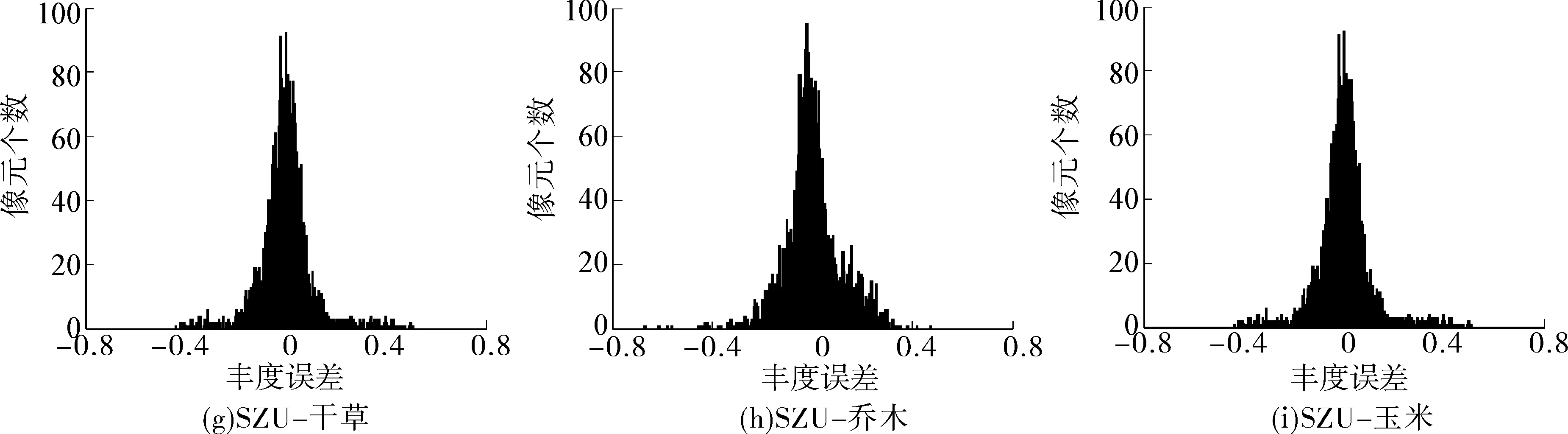
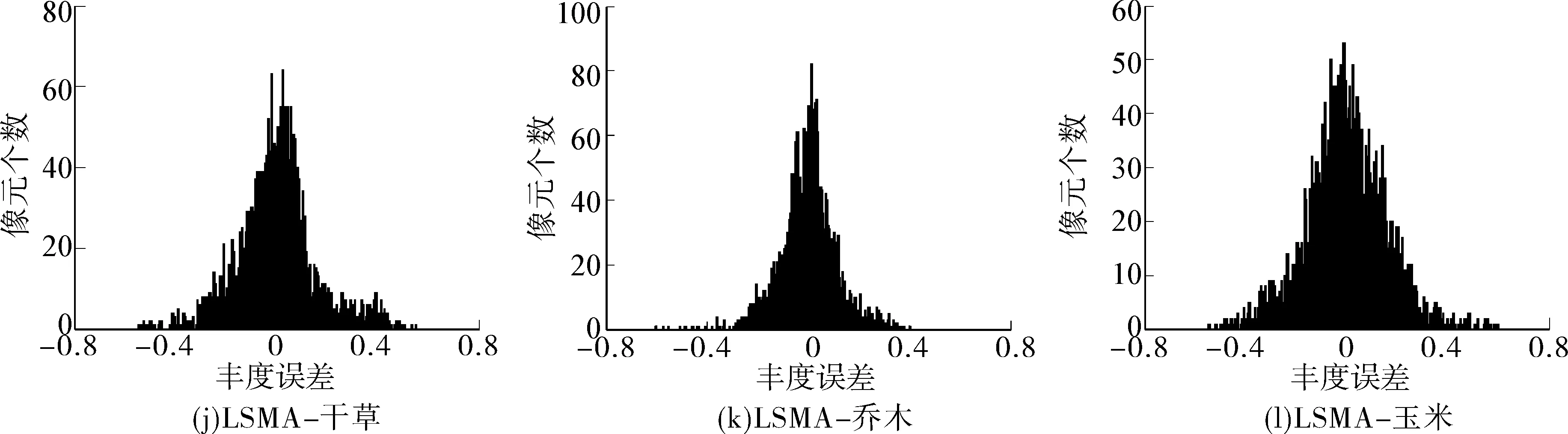
圖6 豐度誤差直方圖

4.3 解混結(jié)果分析

通過上述仿真結(jié)果的對比，可以得到OSPMESMA 算法解混豐度誤差和時間都優(yōu)于其他3種算法，采用正交子空間投影確定像元所屬M-端元組合，避免了不必要端元組合重復(fù)迭代求解，節(jié)約計算時間，同時采用誤差變化量評價標準代替最小均方根誤差，克服了過擬合現(xiàn)象。MESMA 算法需要窮盡所有端元組合，為每個像元尋找到最優(yōu)端元組合，計算時間相當長，通過上述實驗可以看到，隨著端元組合數(shù)的增大，豐度誤差降低很小，而時間卻急速上升，由于尋優(yōu)的過程中，采用最小重構(gòu)均方根誤差為評價標準，會導(dǎo)致過擬合現(xiàn)象，解混時用的端元個數(shù)要大于實際端元個數(shù)，重構(gòu)誤差雖然降低了，但是豐度誤差卻增大了。SZU 算法雖然去除了類內(nèi)光譜變化較大的波段，但是仍然采用固定端元解混，不能有效區(qū)分三類地物。LSMA 算法是傳統(tǒng)固定端元解混，效果最差。

5 結(jié)論

本文提出了一種改進的多端元高光譜解混算法，避免了隨著地物類別以及類內(nèi)光譜個數(shù)的增加，端元組合數(shù)的增大導(dǎo)致計算量的增大，降低了計算復(fù)雜度。同時采用誤差變化代替最小重構(gòu)均方根誤差作為評價標準，避免了過擬合現(xiàn)象。采用模擬數(shù)據(jù)和真實數(shù)據(jù)進行實驗，結(jié)果表明 OSPMESMA 算法解混豐度誤差和時間都優(yōu)于其他3種算法，證明提出的算法可以克服類間光譜變化，多端元解混模型更加合理。在正交子空間投影確定像元 M-端元歸屬時，根據(jù)投影值小于某個很小的閾值來確定，閾值是在多次試驗的基礎(chǔ)上選擇的，如何自適應(yīng)地選擇閾值是下一步工作的重點。

[1]趙春暉, 成寶芝, 楊偉超. 利用約束非負矩陣分解的高光譜解混算法[J]. 哈爾濱工程大學(xué)學(xué)報, 2012, 33(3): 377-382. ZHAO Chunhui, CHENG Baozhi, YANG Weichao. Algorithm for hyperspectral unmixing using constrained nonnegative matrix factorization[J]. Journal of Harbin Engineering University, 2012, 33(3): 377-382.

[2]王立國, 張晶. 基于線性光譜混合模型的光譜解混改進模型[J]. 光電子·激光, 2010, 21(8): 1222-1226. WANG Liguo, ZHANG Jing. An improved spectral unmixing modeling based on linear spectral mixing modeling[J]. Journal of Optoelectronics·Laser, 2010, 21(8): 1222-1226.

[3]王立國, 趙春暉. 高光譜圖像處理技術(shù)[M]. 北京: 國防工業(yè)出版社, 2013：1-20. WANG Liguo, ZHAO Chunhui. Processing techniques of hyperspectral imagery[M]. Beijing: National Defense Industry Press, 2013：1-20.

[4]ROBERTS D A, GARDNER M, CHURCH R, et al. Mapping chaparral in the Santa Monica Mountains using multiple endmember spectral mixture models[J]. Remote Sensing of Environment, 1998, 65(3): 267-279.

[5]ASNER G P, LOBELL D B. A biogeophysical approach for automated SWIR unmixing of soils and vegetation[J]. Remote Sensing of Environment, 2000, 74(1): 99-112.

[6]SOMERS B, DELALIEUX S, VERSTRAETEN W W, et al. An automated waveband selection technique for optimized hyperspectral mixture analysis[J]. International Journal of Remote Sensing, 2010, 31(20): 5549-5568.

[7]SOMERS B, ASNER G P, TITS L, et al. Endmember variability in spectral mixture analysis: a review[J]. Remote Sensing of Environment, 2011, 115(7): 1603-1616.

[8]宋梅萍, 張甬榮, 安居白, 等. 基于有效端元集的雙線性解混模型[J]. 光譜學(xué)與光譜分析, 2014, 34(1): 196-200. SONG Meiping, ZHANG Yongrong, AN Jubai, et al. Effective endmembers based bilinear unmixing model[J]. Spectroscopy and Spectral Analysis, 2014, 34(1): 196-200.

[9]吳波, 張良培, 李平湘. 非監(jiān)督正交子空間投影的高光譜混合像元自動分解[J]. 中國圖象圖形學(xué)報, 2004, 9(11): 1392-1396. WU Bo, ZHANG Liangpei, LI Pingxiang. Unsupervised orthogonal subspace projection approach to unmix hyperspectral imagery automatically[J]. Journal of Image and Graphics, 2004, 9(11): 1392-1396.

[10]DEMARCHI L, CANTERS F, CHAN J C, et al. Mapping sealed surfaces from CHRIS/Proba data: a multiple endmember unmixing approach[C]// Proceedings of the 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS). Reykjavik, 2010: 1-4.

An improved multi-endmember hyperspectral unmixing algorithm

ZHAO Chunhui，CUI Shiling，ZHAO Genping

(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001，China)

The classical multi-endmember spectral mixture analysis model has shortcomings in computation intensity, cumbersome endmember preselection and over-fitting. To overcome these shortcomings, an improved multi-endmember unmixing algorithm is proposed here. Using the characteristics of orthogonal subspace projection that can distinguish signals of interest, it projects pixels onto the orthogonal subspace composed of all of endmembers of the entire surface feature class. Each class selects only one intra-class spectrum. Then it determines the intra-class spectrum of every feature class to which pixels belong according to their projection values. These pixels are isolated in the next iteration in order to reduce computation. Then the optimal number of endmember combinations can be determined according to the reconstruction error variation, which avoids over-fitting. Experiment results show that the inversion abundance error and unmixing time of the improved algorithm are reduced compared to the original algorithm.

hyperspectral unmixing;multi-endmember; unmixing algorithm; orthogonal subspace projection; error variation; intra-class spectral variability

2014-05-17.

時間：2015-07-27.

國家自然科學(xué)基金資助項目(61571145,61405041)；中國博士后科學(xué)基金資助項目(2014M551221)；黑龍江省自然科學(xué)基金重點資助項目(ZD201216)；哈爾濱市優(yōu)秀學(xué)科帶頭人基金資助項目(RC2013XK009003).

趙春暉(1965-), 男, 教授, 博士生導(dǎo)師.

趙春暉，E-mail：zhaochunhui@hrbeu.edu.cn.

10.3969/jheu.201405042

TP751.1

A

1006-7043(2015)09-1281-06

網(wǎng)絡(luò)出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20150727.1254.002.html