基于自適應匹配追蹤的MIMO-OFDM窄帶干擾檢測

畢曉君，夏曉蕾

(哈爾濱工程大學 信息與通信工程學院，黑龍江 哈爾濱 150001)

基于自適應匹配追蹤的MIMO-OFDM窄帶干擾檢測

畢曉君，夏曉蕾

(哈爾濱工程大學 信息與通信工程學院，黑龍江 哈爾濱 150001)

針對基于壓縮感知的MIMO-OFDM窄帶干擾檢測存在檢測時間較長的問題，提出一種基于壓縮感知的自適應匹配追蹤窄帶干擾信號檢測算法。通過建立窄帶干擾在頻域的稀疏模型，提出將目前壓縮感知中解決稀疏信號重構效果較好的自適應匹配追蹤算法應用到窄帶干擾信號檢測中。理論分析與實驗仿真結果表明，在干擾數目增加的情況下，本文算法不僅能夠精準地重構窄帶干擾信號，完成窄帶干擾信號的精確檢測，而且在檢測時間方面具有更為明顯的優勢。

窄帶干擾檢測；自適應匹配追蹤；MIMO-OFDM；信號重構；壓縮感知

近年來MIMO-OFDM技術已成為提高頻譜資源利用率和對抗信道頻率選擇性衰落的有效方法之一，且已被證明可以廣泛應用在WLAN、WI-MAX、4G以及Wi-Fi中[1]。然而，窄帶干擾的存在使MIMO-OFDM系統的誤碼率急劇上升，系統性能受到了嚴重的影響[2]。因此在實際應用中，為了保證MIMO-OFDM系統的可靠通信，對窄帶干擾進行準確地檢測很有必要[3]。對于MIMO-OFDM系統窄帶干擾的檢測，相關文獻已經提出了一些算法，主要有時域和頻域兩種[4]。時域算法不會損害信號，并能以最接近窄帶干擾的形式對窄帶干擾進行消除[5-6]，但誤碼率較高，時間過長，不滿足通信實時性的要求。頻域算法[7-8]以文獻[8]中的陷波干擾抑制為主，但此方法也存在時間較長的問題。2011年文獻[9]提出一種基于壓縮感知的MIMO-OFDM窄帶干擾檢測技術，該方法將窄帶干擾檢測轉化為稀疏信號的重構問題，在低于奈奎斯特采樣率條件下，成功地實現了單個及多個窄帶干擾的檢測，與傳統方法相比，該方法在很大程度上提高了窄帶干擾檢測的精度，但因為其算法復雜度高，所以檢測時間較長，尤其當子載波數成倍增加，信號維數大幅增加時，不能滿足系統的實時應用性。針對文獻[9]存在的缺點，本文將目前壓縮感知中解決稀疏信號重構效果較好的自適應匹配追蹤(sparsity adaptive matching pursuit, SAMP)算法[10]運用MIMO-OFDM通信系統的窄帶干擾信號檢測中，該算法由國外學者于2008年提出，在解決實際壓縮感知問題上取得了良好的效果。但直至2012年才被引入國內，并成功應用在圖像處理領域。本文首次將SAMP算法應用于解決MIMO-OFDM系統的窄帶干擾檢測問題中，在保證檢測精度的前提下，快速地完成窄帶干擾信號的重構。

1 MIMO-OFDM系統模型

1.1 MIMO-OFDM通信系統模型

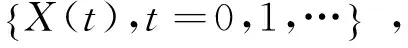
(1)

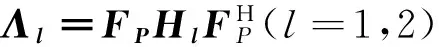
為了實現MIMO-OFDM系統的窄帶干擾檢測，文獻[9]通過分析窄帶干擾的特性，首先對窄帶干擾進行建模，其次是頻域加窗來完成對接收信號的處理，下面詳細介紹其實現過程。

1.2 基于壓縮感知的MIMO-OFDM窄帶干擾檢測

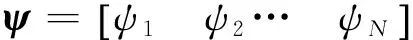
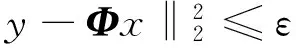
(2)

式中：ε是一個很小的常量。

根據窄帶干擾在頻域的稀疏性，文獻[9]對其在頻域進行建模:

(3)

式中：Ji是在第i個子載波上的窄帶干擾信號，di是其幅值，f和t分別為窄帶干擾影響的子載波位置。

為了增強窄帶干擾的稀疏性，即減少發送信號和窄帶干擾之間的頻偏對窄帶干擾頻域稀疏性造成的影響，文獻[9]在對接收信號進行快速傅里葉變換之前，采用海寧窗對信號進行加窗處理:

Y(0)=FPΛWy(0)=HWΛ1VX(0)+

HWΛ2VX(1)+Jeqv+Z(0)

(4)

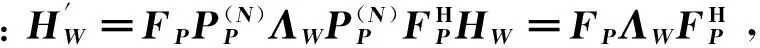
因此可以看出，Jeqv作為窄帶干擾信號J的等效形式，這一變換并不影響窄帶干擾Jeqv的稀疏性，仍是與J具有相同稀疏性的稀疏矩陣。

同理，將Y(0)和Y(1)疊加，即可得到：

(5)

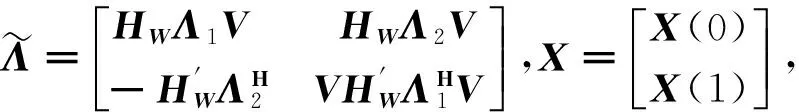
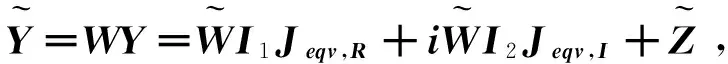
(6)

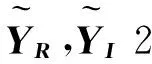
(7)

(8)

式(8)目的是要對窄帶干擾J進行檢測，而J在頻域是稀疏的。所以，對窄帶干擾J的檢測問題可轉化為如式(9)所示的壓縮感知稀疏信號的重構問題，其中ε是噪聲平均能量。

(9)

從式(9)可以看出，將MIMO-OFDM通信系統中的窄帶干擾J看做待重構的稀疏信號，可以采用壓縮感知的重構算法對窄帶干擾信號進行重構，從而完成對窄帶干擾的檢測。

2 基于SAMP算法的MIMO-OFDM系統窄帶干擾檢測算法實現

在實際應用中，信號的稀疏度大多都是未知的，特別是窄帶干擾信號，因此本文將采用信號稀疏度自適應的SAMP算法。該算法屬于貪婪追蹤算法，可以在未知稀疏度情況下準確地對窄帶干擾信號進行重構，這對于解決實際中稀疏度未知的信號重構問題是非常有效的。在對MIMO-OFDM系統的窄帶干擾進行檢測時，SAMP算法將自適應與回溯相結合，同時兼顧了重構的性能和精度，可以更好地對窄帶干擾信號進行重建，并完成窄帶干擾檢測。

文獻[9]采用基本的壓縮感知算法實現了MIMO-OFDM系統的單個和多個窄帶干擾的檢測，很大程度上提高了檢測精度，但是算法的復雜度高、運行時間較長，不能很好地滿足系統實時性要求。

結合式(9)，用于窄帶干擾檢測的SAMP算法流程如下：

1)初始化

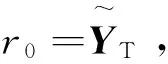
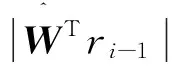
3)更新候選集：Ci=Ti-1∪Si。

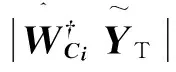
6)若‖r‖2≤ε，則跳出循環體；否則進一步判斷：若‖ri‖2≥‖ri-1‖2，則轉入下一階段，即j=j+1，k=j×s;否則，繼續在本階段里迭代，即Ti=T，i=i+1。

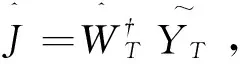
其中,(·)?表示偽逆運算。

為了便于理解，圖1給出了本文提出算法的流程圖。

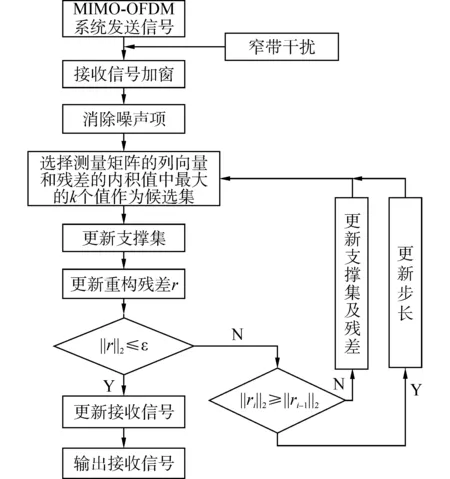
圖1 基于SAMP算法的MIMO-OFDM窄帶干擾檢測流程Fig. 1 Narrow band interference detection of MIMO-OFDM with SAMP

從上述步驟2)中可以看出，在算法運行過程中，選擇將測量矩陣與殘差向量內積最大的項保留下來，在步驟3)～6)中采用回溯的思想，將當前選出的集合與之前迭代得到的支撐集合并，這樣就使得算法能夠快速收斂。并且在步驟6)中，通過比較當前殘差與閾值的大小來判定算法是否停止，如果算法沒有停止，則根據當前代數對步長進行自適應調整，使算法能快速逼近信號的稀疏度，這不僅使SAMP算法能夠快速對稀疏度未知的窄帶干擾信號進行重構，而且能夠保證重構的精度。

3 實驗仿真與結果分析

為了驗證本文所提算法的有效性和先進性，這里將分別針對MIMO-OFDM系統中的單個窄帶干擾和多個窄帶干擾進行仿真實驗，并與文獻[9]進行對比，衡量指標采用通信系統常見的誤碼率和窄帶干擾檢測時間。

實驗環境的硬件配置為：Intel(R)Pentium(R)CPUG620@ 2.60GHz、2G內存的計算機上進行,開發環境為MATLAB2012。

3.1 實驗參數設置

為了便于對比，仿真實驗的具體參數與文獻[9]相同：發射天線NT=2，接收天線NR=1 的MIMO-OFDM通信系統，子載波數N=320,保護間隔G=N/4=80，采用16QAM調制，發射信號和窄帶干擾都經過4徑瑞利衰落的無線信道，通過海寧窗函數對接收端的信號進行加窗處理。

3.2 單個窄帶干擾檢測的仿真實驗

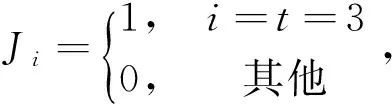
不失一般性，本文首先對MIMO-OFDM系統中的單個窄帶干擾進行實驗檢測，并與目前檢測效果最好的文獻[9]進行對比。圖2為信噪比為0～20dB時，本文算法和文獻[9]中算法的仿真實驗結果。

圖2 單個窄帶干擾檢測Fig. 2 Single narrow band interference detection

由圖中可以看出，當系統存在單個窄帶干擾時，系統誤碼率很高，且不再隨信噪比改變，系統性能受到了嚴重影響。但當采用這兩種算法對窄帶干擾進行檢測并消除后，系統誤碼率減小，性能得到了很大的提高。且信噪比在0～18dB時，本文算法和文獻[9]的算法系統誤碼率基本一致，與無窄帶干擾曲線幾乎重合；但當信噪比在18～20dB時，本文算法能夠以較高精度地檢測窄帶干擾，誤碼率略小于文獻[9]的算法，可見本文算法性能較優于文獻[9]的算法。

3.3 多個窄帶干擾檢測的仿真實驗

不失一般性，本文對MIMO-OFDM系統中的多個窄帶干擾進行實驗檢測，并與目前檢測效果最好的文獻[9]進行對比。圖3為信噪比為0～20dB、窄帶干擾個數為3時，2種算法的仿真實驗結果。

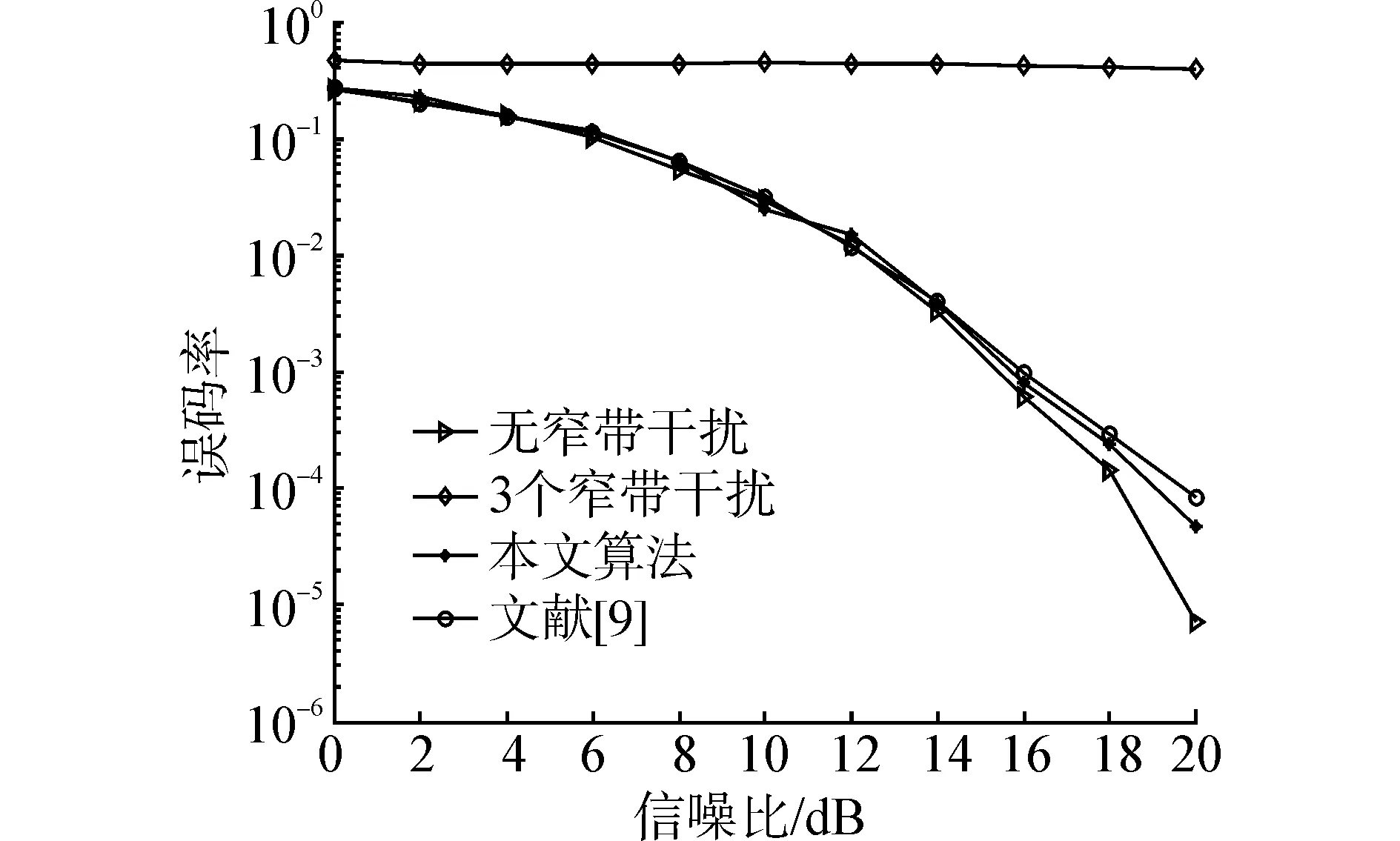
圖3 多個窄帶干擾檢測Fig. 3 Multiple narrow band interference detection

由圖3中可以看出，當信噪比在0～14dB時，與理想無窄帶干擾的誤碼率曲線相比，本文算法和文獻[9]的算法與無窄帶干擾的誤碼率曲線非常接近，可以看出兩種算法都能夠以較高精度檢測窄帶干擾；在信噪比在14～20dB時，本文算法和文獻[9]的算法均略高于無窄帶干擾時系統的誤碼率，但仍滿足系統對誤碼率的要求，且本文算法的誤碼率始終小于文獻[9]算法的誤碼率。這說明在對MIMO-OFDM系統中的多個窄帶干擾進行檢測時，本文算法較文獻[9]的算法效果較好。

為了驗證本文算法在檢測時間上的優越性，這里進行了單個和多個窄帶干擾的檢測時間測試。表1給出了窄帶干擾個數不同時，兩種算法的檢測時間對比。

表1 2種算法檢測時間對比

Table 1 Detection time of the two algorithms s

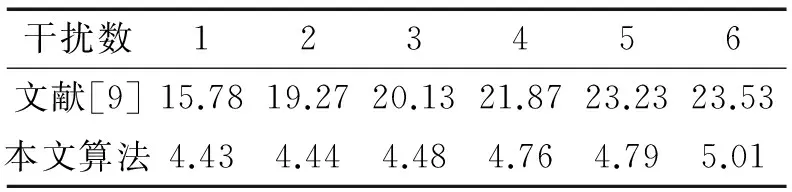
干擾數123456文獻[9]15.7819.2720.1321.8723.2323.53本文算法4.434.444.484.764.795.01

從表1中可以看出，隨著窄帶干擾數目的增加，兩種算法的檢測時間都隨之增加。但本文算法有明顯的優勢，首先，文獻[9]的檢測時間平均在20.64 s，而本文算法的檢測時間僅為4.65 s，整體上更好地滿足了系統實時性的要求，究其原因在于文獻[9]進行信號重構時約束項過多，導致其算法復雜度高；其次，隨著干擾數目的增加，文獻[9]的檢測時間大幅增加，而本文算法則增加較少，說明本文算法與文獻[9]相比在干擾數增加時優勢明顯。而對于實際MIMO-OFDM系統，通常子載波數成倍增加，信號維數大幅增加，將增加窄帶干擾數目，這個優勢將尤為重要。

4 結束語

將壓縮感知理論應用于MIMO-OFDM系統是一個比較前沿的課題，本文提出了一種基于SAMP的MIMO-OFDM窄帶干擾檢測算法，通過將自適應和回溯思想的有機結合，能夠更好地兼顧重構的性能和復雜度，大大縮短檢測時間。實驗結果表明，該方法與目前在MIMO-OFDM窄帶干擾檢測問題中效果最好的算法相比，在保證較高檢測精度的情況下，對單個窄帶干擾和多個窄帶干擾均可以實現快速準確檢測，具有更強的實時性，特別是在信號維數大幅增加、子載波數成倍增加時更具優勢，在實際應用中具有較好的推廣價值。

[1]PHAM T H, LIANG Y, ZENG Y, et al. Channel information estimation and data detection for MIMO-OFDM systems under unknown narrowband interference[C]//Wireless Communications and Networking Conference. Shanghai, China, 2013: 3958-3963.

[2]MORELLI M MORETTI M. Improved decoding of BICM-OFDM transmissions plagued by narrowband interference [J]. IEEE Transactions on Wireless Communications, 2011, 10(1): 20-26.

[3]MITHUNA D, PREMA G. Compressive sensing algorithm for narrowband interference mitigation in MIMO-OFDM[C]// 2012 IEEE International Conference on Advanced Communication Control and Computing Technologies. Ramanathapuram, India, 2012: 22-27.

[4]DARSENA D, GELLI G, VERDE F. Perfect symbol recovery and NBI suppression in MIMO-OFDM systems[J]. Electronics Letters, 2014, 50(3): 225-227.

[5]WANG J. Adaptive filter for suppressing narrow-band interference in DSSS communication[C]//Computer Science and Service System (CSSS), 2011: 162-165.

[6]KUMBHANI B, REDDY T S, SASTRY K S, et al. Narrow band interference (NBI) mitigation technique for TH-PPM UWB systems in IEEE 802.15.3a channel using wavelet packet transform[C]//Emerging Trends and Applications in Computer Science (ICETACS), 2013: 38-42.

[7]付衛紅, 宋長漢, 黃坤. 基于差分求門限的變換域窄帶干擾抑制[J]. 電子與信息學報, 2013, 35(12): 296-2965. FU Weihong, Song Changhan, HUANG Kun. Narrow-band interference suppression in transform domain based on difference-cluster-threshold algorithm[J]. Journal of Electronics & Information Technology, 2013, 35(12): 2960-2965.

[8]HAN M, YU T, KIM J, et al. OFDM channel estimation with jammed pilot detector under narrow-band jamming[J]. IEEE Transactions on Vehicular Technology, 2008, 57(3): 1934-1939.

[9]AHMAD G, AL-DHAHIR N. A sparsity-aware approach for NBI estimation in MIMO-OFDM[J]. IEEE Trans on Wireless Communications, 2011, 10(6): 1854-1862.

[10]DO T T, LU Gan, NGUYEN N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//2008 42nd Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, 2008: 581-587.

[11] DUARTE M F, ELDAR Y C. Structured compressed sensing: From theory to applications[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4053-4085.

[12]MATTINGLEY J, BOYD S. Real-time convex optimization in signal processing[J]. IEEE Signal Processing Magazine, 2010, 27(3): 50-61.

Narrow band interference detection for MIMO-OFDM systems based on sparsity adaptive matching pursuit

BI Xiaojun，XIA Xiaolei

(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)

At present, narrow band interference detection in MIMO-OFDM based on compressed sensing takes too long. To solve this problem an adaptive matching pursuit algorithm was proposed based on compressed sensing. A sparse model of narrow band interference in the frequency domain was established. This algorithm is good at solving sparse signal reconstruction, and thus it was applied to narrowband interference signal detection. The theoretical analysis and experimental simulation results show that with the increase of interference, the algorithm in this paper can not only be used to reconstruct narrow-band interference signals accurately and detect narrow band interference signals precisely, it also has a more obvious advantage in shorter detection time.

narrow band interference detection; sparsity adaptive matching pursuit; MIMO-OFDM; signal reconstruction; compressed sensing

2014-07-07.

時間：2015-07-15.

國家自然科學基金資助項目(61175126)；中央高校基本科研業務費專項資金資助項目(HEUCFZ1209)；教育部博士點基金資助項目(20112304110009).

畢曉君(1964-)，女,教授，博士生導師.

畢曉君，E-mail：bixiaojun@hrbeu.edu.cn.

10.3969/jheu.201407009

TU832

A

1006-7043(2015)09-1287-05

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20150715.1727.005.html