五冗余捷聯慣組最優配置設計①

武唯強，陳 康，閆 杰

(西北工業大學 航天學院，西安 710072)

?

五冗余捷聯慣組最優配置設計①

武唯強，陳 康，閆 杰

(西北工業大學 航天學院，西安 710072)

導航制導系統的高可靠性直接決定了固體運載火箭飛行任務完成的質量，而慣組冗余技術是目前提高系統可靠性的主要方式之一。文章以固體運載火箭導航系統中一種三正交兩斜置的五冗余捷聯慣組配置方式為對象，以導航性能指標最優為目標函數，構造了最優配置下的非線性矛盾方程組，采用最小二乘法求解得到最佳逼近解，得到五冗余捷聯慣組的最優配置，并通過仿真進行了驗證。結果表明，三正交兩斜置的五冗余捷聯慣組最優配置共有24組解，其全部解的導航性能指標均為1.424 3；當某個正交軸出現故障時，能夠從斜置軸信息中重構出正交軸信息，以保證導航信息的準確性和精度，且導航誤差在5倍陀螺器件自身誤差當量之內。

冗余系統；捷聯慣組；優化；配置

0 引言

慣性導航系統是利用陀螺儀和加速度計等慣性敏感元件在飛行器等載體內部測量載體相對慣性空間的位置、速度和姿態的自主式導航系統，在固體火箭及其他飛行器中有著廣泛的應用。導航系統的高可靠性直接決定了飛行器飛行任務完成的質量，而冗余技術就是提高導航系統可靠性的最有效辦法之一[1]。冗余技術按照工作方式可分為系統冗余與單元級冗余，由于單表冗余局部冗余可靠性提高明顯，目前在慣導系統中的應用也最為廣泛[2]。典型的冗余安裝結構包括：(1)三三結構，由3個相同的非冗余正交配置的 IMU 子系統并行構成的冗余配置結構[3]；(2)二自由度陀螺斜置配置，陀螺的自轉軸分別垂直其4個側面，相應的2個測量軸分布在側面里，并沿側面角平分線軸對稱，這種結構保證了在相同數目二自由度陀螺構成的元件冗余系統中能達到最大的可靠度[3]；(3)圓錐體結構,當傳感器的數目大于或等于4個時(通常是5個或6個)，將傳感器按其測量軸沿圓錐母線均勻安裝在一個固定圓錐角的圓錐面上[4]；(4)六傳感器正十二面體結構，將6個傳感器的測量軸與正十二面體的平行面互相垂直[4]。對于不同的冗余配置結構，主要需要研究捷聯慣導系統合理的冗余配置方法，分析不同配置情況下對系統導航性能精度的影響，保證系統在無故障和故障情況下都可穩定可靠的工作[5]。

本文主要針對一種應用在固體火箭系統中的三正交兩斜置的冗余慣組系統進行研究，通過分析該類冗余系統在無故障模式和故障模式下的導航性能指標，推導出導航精度最高的最優配置方案，并通過仿真進行了驗證。

1 五冗余捷聯慣組配置方案

捷聯慣性測量組合(捷聯慣組)是固體運載火箭控制系統的重要箭上設備之一。通過合理的對慣性器件進行配置，箭載計算機采集慣組陀螺儀和加速度計輸出，經過慣組冗余提供箭體坐標系的角速度和角加速度信息，進行姿態角、導航、制導計算。本文所研究的五冗余捷聯慣組配置形式采用三正交軸及兩斜置軸(各軸均配置1個陀螺儀和加速度計)的配置結構，具體安裝方案如圖1所示。

圖1 三正交兩斜置的配置方案Fig.1 Configuration model of the two orthogonaloblique solids

圖1中g1、g2、g3、g4、g5為各軸安裝的陀螺儀，a1、a2、a3、a4、a5為加速度計。其中，g1、g2、g3以及a1、a2、a3分別沿X、Y、Z三正交軸正向放置，g4、g5以及a4、a5沿任意方向的2個斜置軸放置。慣組坐標指向為X向前，Y向上，Z與X、Y遵從右手定則。圖1中，各參數的定義如下：L、K分別為任意斜置放置的測量組件在XOZ平面上的投影線；α1、α2分別為從Y軸順時針旋轉至第四、五測量組件所在斜置軸的角度；β1、β2分別為從Z軸逆時針旋轉至L、K的角度。

此時的配置矩陣為

(1)

2 最優配置結構設計

在冗余配置的捷聯慣性導航系統中，慣組系統的輸出方程為[6]

Z=Hω+ε

(2)

式中Z∈R3為待測量的導航信息；ω∈Rn為n個慣性器件的測量值(n≥3)；H為慣導系統的測量矩陣；ε為零均值的高斯白噪聲。

對于本文所研究的三正交兩斜置五冗余捷聯慣組系統，對其進行最優配置的目標是保證慣組系統在正常或故障情況下，均能保證導航精度最優。

2.1 無故障情況下導航性能指標分析

在對冗余配置進行優化設計時，可從3種導航性能指標進行分析。

假設量測噪聲ε=(e1，e2，…，em)T，噪聲中各分量是相互獨立的隨機常數，該種情況下，其導航性能指標為

(3)

其中

M=(HTH)-1HT

為測量噪聲對3個坐標軸方向的影響程度。在此基礎上，推廣到含有加權因子的性能指標：

(4)

假設V是均值為零、方差為σ2的隨機矢量，則性能指標為

(5)

式中ai為加權因子；G-1=HTH；G(i，i)是G的第i個對角線元素。

在慣性器件的測量精度一定的情況下，測量誤差對正交軸的影響直接取決于(HTH)-1的大小。常用的是假設V是均值為零的高斯隨機向量，可定義如下的性能指標：

(6)

當不考慮加權因子時，以上3種性能指標的優化條件是一致的[7]。如果冗余慣組的安裝矩陣H能夠使Fp的值最小，則由噪聲所產生的導航誤差最小，即慣組系統可獲得最佳的導航性能。

2.2 故障情況下導航性能指標分析

由2.1節分析可知，配置方案的3種性能優化指標具有一致性，為統一標準，在本節中全部采用性能指標Fp1進行分析。

對于本文所研究的五冗余捷聯慣組測量組件，在各軸器件均正常工作的情況下，性能指標函數為

當系統中的1組測量組件出現故障時，該指標函數不適用，需要進行改進。故當1組測量組件出現故障時，性能指標為

(7)

其中

最優配置結構不但要保證測量組件全部正常工作時的測量噪聲對正交軸的誤差影響最小，而且在出現故障的情況下，相應的性能指標也能達到最小。根據性能指標Fp1，只要指標函數式(7)達到最小，則此時的配置結構即為最優。

2.3 導航性能最優充要條件

由式(2)可知，H的每行分別是m個測量軸的方向余弦，則

tr(G-1)=tr(HTH)=m

(8)

記λ1、λ2、λ3分別是矩陣G-1的特征值，由于G-1是對稱陣，因此存在正交矩陣P，使得：

PG-1PT=diag(λ1，λ2，λ3)

(9)

tr(G-1)=λ1+λ2+λ3=m

(10)

由式(9)可知：

(11)

因此，在優化條件(10)下，可得到Fp1最優時，對特征值的要求為

λi=m/3，i=1，2，3

(12)

此時，導航性能指標Fp1的值最小：

(13)

由上式可知，導航性能指標最優的充要條件為安裝矩陣H滿足：

G-1=(m/3)I

(14)

即H各列的模都是m/3，各列之間相互正交。

當λ1=λ2=λ3=n/3時，該不等式的等號成立，此時的導航性能指標J取極小值。因此，此時的安裝矩陣H是導航性能指標最優的測量矩陣。

必要性證明：如果安裝矩陣H的配置使導航性能最優，這意味著導航性能指標J最小。

已知：

且

trace(HHT)=λ1+λ2+λ3

則可得

λ1=λ2=λ3=n/3

(15)

(16)

可得：

(17)

2.4 最優配置解算

由以上對導航性能最優條件下最優配置的充分必要條件可知，對于本文所研究的三正交兩斜置五表冗余系統，要達到最優配置，配置矩陣需滿足以下關系：

(18)

此時得方程組：

(19)

該方程組為一矛盾方程組，將方程組(9)線性化為

A=sin2α1sin2β1

B=sin2α2sin2β2

C=cos2α1

D=cos2α2

E=sinα1cosα1sinβ1

F=sinα2cosα2sinβ2

G=sin2α1sinβ1cosβ1

H=sin2α2sinβ2cosβ2

M=sinα1cosα1cosβ1

N=sinα2cosα2cosβ2

則原方程組可化簡為矩陣的形式：

aX=b

(20)

其中

分塊矩陣：

a12=O3×4，a21=O2×6

這里，因為rank(a)=5，因此線性方程組aX=b是不相容的，傳統的最小二乘法不能使用，這里采用改進方法求取不相容線性方程組的最佳逼近解[6]。

設V是歐氏空間，又x，y∈V，則x-y的長度|x-y|稱為向量x與y的距離。

定義：設線性方程組AX=b(A=(aij)m×n，m>n，b=(b1，…，bm)T，x=(x1，x2，…，xn)T，xi∈R是不相容的，則滿足AT(AX-b)=0…*的X稱為AX=b的一個近似解[6]。

定理1[7]：凡滿足(*)式的X必是不相容線性方程組AX=b的一個最佳逼近解。

定理2[7]：不相容方程AX=b必有唯一LNLS解，X=A+b(A+是A的M-P廣義逆)。

求解線性方程組(10)可為

(21)

由于α1∈[0，π]，α2∈[0，π]，β1∈[-π，π]，β2∈[-π，π]，故方程組(21)的解為

α1=54.734 7°或α1=125.264 4°

α2=54.734 7°或α2=125.264 4°

β1=±45°或β1=±135°

β2=±45°或β2=±135°

將以上計算結果再次代入到方程組(19)中，那么會有24組配置結構，各配置結構下的導航性能指標如表1所示。

3 仿真驗證

在得到五冗余捷聯慣組的最優配置后，可通過故障模式下對各冗余軸進行導航信息重構的方式考核最優配置的正確性。

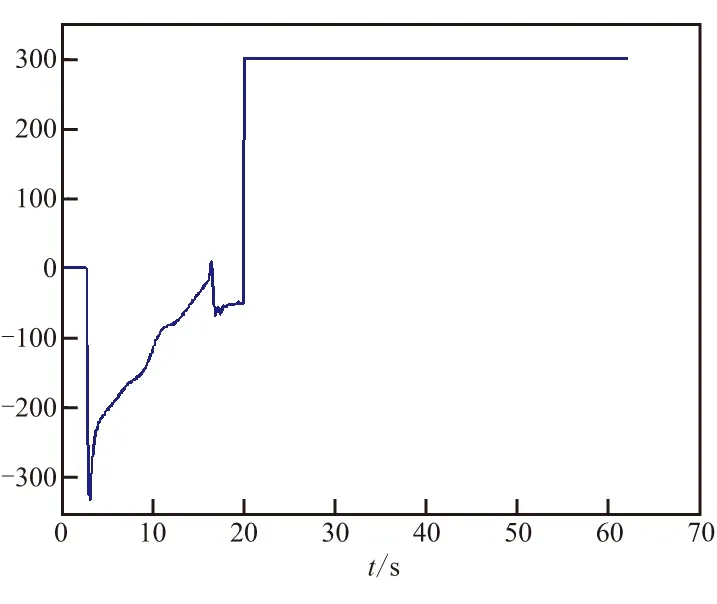
假定五冗余捷聯慣組的正交軸X陀螺器件發生輸出故障，故障類型為常值輸出，故障從第20 s開始，通過最小二乘估計的方法從斜置軸測量值進行導航信息重構，重構方法為

(22)

式中Zi為其他4個慣組器件的輸出信息。

此時，信息重構的估計均方誤差為

(23)

仿真中使用的陀螺誤差模型參數如表2所示。

表1 最優配置及性能指標Table 1 Optimal Configuration and performance index

表2 陀螺誤差模型參數Table 2 Error parameter of the gyro

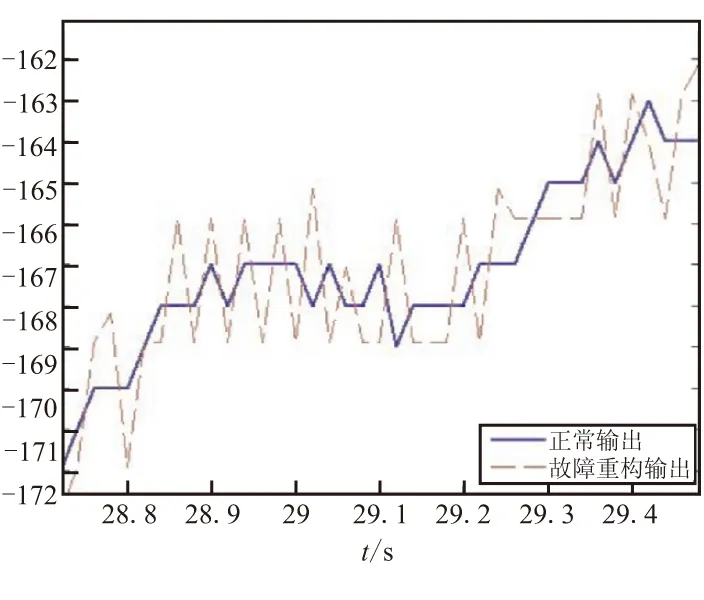
未發生故障和已經發生故障陀螺脈沖輸出時間序列如圖 2所示，經過信息重構正交軸X陀螺脈沖輸出如圖3所示。

由故障模式下重構的導航系統輸出可看到，在最優配置模式下，當五冗余捷聯慣組某個正交軸出現故障時，通過信息重構可由其他斜置軸的信息準確估計出故障軸的導航信息，且重構誤差不大于5倍陀螺器件自身誤差當量，從而保證導航系統的精度能滿足固體火箭的制導控制要求。

(a)正常工作

(b)故障模式

(a)輸出結果

(b)局部放大

4 結論

(1)三正交兩斜置冗余慣組系統存在最優逼近解，其最優配置形式有24種，均可保證在無故障和故障模式下的導航性能最優。

(2)當三正交兩斜置冗余慣組正交軸出現故障時，可通過斜置軸重構出故障軸的導航信息，在最優配置模式下，導航精度小于5倍陀螺器件自身誤差當量。

[1] 李雪蓮,孫堯,莫宏偉.一種基于MIMU的九陀螺冗余配置[J].哈爾濱工業大學學報,2009,41(5):90-94.

[2] Daly K C,Gai E and Harrison J V Generalized likelihood test for FDI in rendundant sensor configurations[J].Journal of Guidance and Control,1979,2(2):9-17.

[3] Hirokimi S.Study on strapdown inertial navigation redundant sensor system[J].NALTR-660.1981-03.

[4] Harrison J V,Gai E G.Evaluating sensor orientantions for navigation performance and failureDetection[J].IEEE Transaction on Aerospace and Electronic System,1977,AES_13(6):631-643.

[5] 潘鴻飛,袁立群,任尚云,捷聯慣導陀螺儀冗余配置研究[J].飛航導彈,2003(2):52-56.

[6] 李宏年,孫云剛,劉菁.不相容線性方程組的最小二乘解[J],青海大學學報(自然科學版),2002,20(1):49-50.

[7] Yuksel Y. Design and analysis of inertial navigation systems with skew redundant inertial sensors[D].Canada:University of Calgary,2011.

(編輯：呂耀輝)

Optimal configuration design of redundant strapdown inertial system with five axes

WU Wei-qiang，CHEN Kang，YAN Jie

(College of Astronautics,Northwestern Polytechnical University,Xi'an 710072,China)

High reliability of navigation and guidance system directly determines the quality for solid launch vehicles to accomplish flight missions,while redundant inertial measurement technology is one of the main ways to increasing the system reliability.In this paper,taking a redundant configuration of strapdown inertial system with five axes(three on the spindles and two on the oblique axis)applied in solid launch vehicles as the research object and optimization of navigation performance index as objective function,nonlinear contradiction equations under optimal configuration were derived and the optimal imminent solutions were calculated by least square method,then finally the optimal configuration for redundant strapdown inertial system was obtained,which was also verified by simulation.The results demonstrate that there are 24 solutions for the optimal configuration for redundant strapdown inertial system with five axes(three on the spindles and two on the oblique axis),all of which have a navigation performance index of 1.424 3 and when the fault happens in spindles,the configuration can reconstruct their information to ensure the accuracy and precision of navigation information with the navigation error within 5 times the error equivalence of gyro units.

redundancy system；strapdown inertial measurement unit；optimization；configuration

2014-05-21；

：2014-08-07。

中國航天科技集團公司航天支撐基金(2013-HT-XGD-15)。

武唯強(1971—)，男，博士，研究方向為飛行器總體設計。E-mail：wangyinan@nwpu.edu.cn

V448

A

1006-2793(2015)01-0018-05

10.7673/j.issn.1006-2793.2015.01.004