基于新特征優勢關系的粗糙決策分析模型

鮑忠奎，楊善林

（1.合肥工業大學 管理學院，合肥 230009；2.安徽大學 數學科學學院，合肥 230601）

0 引言

波蘭數學家Pawlak提出的粗糙集理論[1]，是一種處理含糊和不確定信息的新型數學工具，近年來引起了人們的極大關注，已在機器學習、歸納推理、模式識別、決策分析等方面取得非常成功的應用。Greco等利用序決策系統中屬性值之間遞增或遞減的序關系，用優勢關系代替經典粗糙集中的等價關系，提出基于優勢關系的粗糙集理論[2-4]]，為經濟、管理等領域中大量存在的多屬性決策問題提供了一個新的研究思路。然而，序決策系統中的很多屬性值在獲取過程中往往因為種種原因，丟失或無法獲得。因此如何在不完備序決策系統中進行優勢關系的粗糙集拓展成為研究的熱點。

目前，已有文獻[5-9]對不完備序決策系統中優勢關系的拓展主要是基于對未知屬性值的兩種不同語義解釋：（1）所有的未知屬性值僅僅是被遺漏的，但又是確實存在的，是一種遺漏型的未知屬性值；（2）所有的未知屬性值被認為是缺席的，是不允許被比較的，是一種缺席型的未知屬性值。文獻[5～8]從遺漏型未知屬性值角度出發，分別提出了基于擴展優勢關系、廣義擴展優勢關系、限制擴展優勢關系的拓展粗糙決策分析模型，對目標對象的分類更加準確，符合實際；文獻[9]從缺席型未知屬性值的角度出發，綜合相似關系與優勢關系的優點，提出了基于相似優勢關系的粗糙決策分析模型，并利用拓展的相似優勢關系解決了不完備序決策系統中的屬性約簡等問題。然而，以上文獻均假定不完備序決策系統中的未知屬性值僅有一種可能的語義解釋，即遺漏型或缺席型的，但在現實信息系統中，未知屬性值往往既有遺漏型也有缺席型的，針對同時具有缺席和遺漏型未知屬性值的廣義不完備序決策系統，如何拓展粗糙集模型進行決策分析呢。

文獻[10]在同時具有缺席和遺漏型未知屬性值的廣義不完備序決策系統中提出了特征優勢關系的概念，并給出了基于特征優勢關系的屬性約簡方法。文獻[11]在廣義不完備序決策系統中給出擴展的優勢特征關系，集中討論了屬性值粗化細化時，上下累積集的增量更新規律及其算法。但兩文在處理遺漏型未知屬性值時，為討論方便，均認為其可以等于任意值，既優于任意值又劣于任意值，顯然這對未知屬性值的要求太過寬松，容易將不屬于同一類的對象誤分到同一類中，影響粗糙集模型的應用效果。本文針對這一問題，深入分析屬性值域的偏序關系，在廣義不完備序決策系統中提出一種新特征優勢關系，并依據定義的新特征優勢關系給出累積集的近似集和邊界，從而獲取分類決策規則。同時與已有的基于特征優勢關系的粗糙決策模型進行了對比分析，理論和實例均驗證了基于新特征優勢關系的粗糙決策模型的有效性和實用性。

1 基本概念

1.1 廣義不完備序決策系統

1.2 向上累積集和向下累積集

假設決策屬性集D把論域U分成有限的決策類，CL={Clt，t∈T}，T={1，2，…，n}，每個對象屬于一個且僅屬于一個決策類Clt，并且假定這種分類是有序的，即對于所有的r，s∈T，若r＞s，則Clr中的對象優于Cls中的對象。為了處理多屬性的偏好信息，定義兩種累積集。

定義1設Clt是一決策類，定義向上累積集和向下累積集分別為：

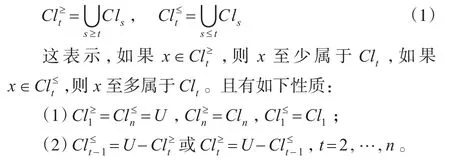
1.3 特征優勢關系

定義2給定廣義不完備序決策系統S′=＜U，AT∪D，V，f＞ ，集合 P?AT ，P 上的特征優勢關系CD(P)定義為：

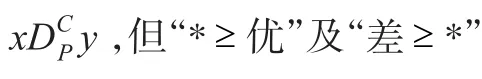
2 基于新特征優勢關系的粗糙決策分析模型

2.1 新特征優勢關系

新特征優勢關系充分利用優勢關系中屬性值域的偏好次序，既保留了缺席型未知屬性值不允許被比較的特點，又對確實存在且僅是被遺漏的遺漏型未知屬性值進行了有效的約束。當決策系統S′中的所有未知屬性值都被看作是遺漏型時，特征優勢關系則退化為限制擴展優勢關系[8]；當S′中的所有未知屬性值都被看作是缺席型時，特征優勢關系則退化為相似優勢關系[9]，所以新特征優勢關系是限制擴展優勢關系和相似優勢關系的進一步推廣，對于信息不完全樣本對象的分類更加符合實際。

由定義知，新特征優勢關系具有下列性質：

性質1新特征優勢關系滿足自反性和傳遞性，對稱性不一定滿足。

（2）證明同（1）。

定理1表明了P的特征優勢集與P的特征劣勢集之間的關系。

2.2 基于新特征優勢關系的粗糙近似

2.3 基于新特征優勢關系的決策規則

（1）根據式（6）可得以下決策規則：

3 與已有特征優勢關系下的粗糙決策模型的對比

3.1 與已有特征優勢關系的比較

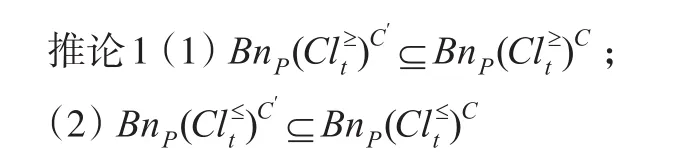
3.2 近似分類性能的對比

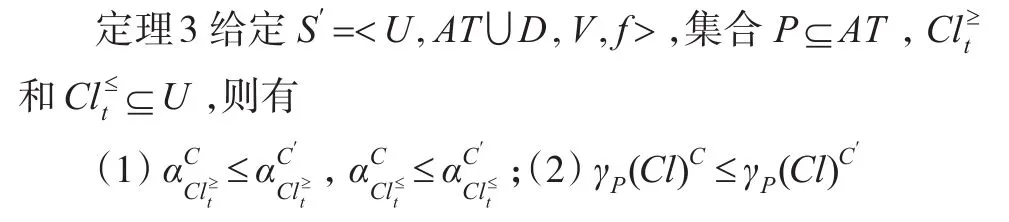
證明由定義6、7和定理2及其推論1易得。

定理3表明，基于新特征優勢關系的粗糙決策模型的近似分類精度和近似分類質量都要高于已有的特征優勢關系下的粗糙決策模型的近似分類精度和近似分類質量，即本文提出的拓展粗糙集決策分析模型要優于已有的決策分析模型。

4 應用舉例

表1為某班級教師對部分學生的一個綜合評價表（表中的“？”表示該生沒有選修相應的課程，“*”表示該生選修了相應課程，但成績弄丟了）。

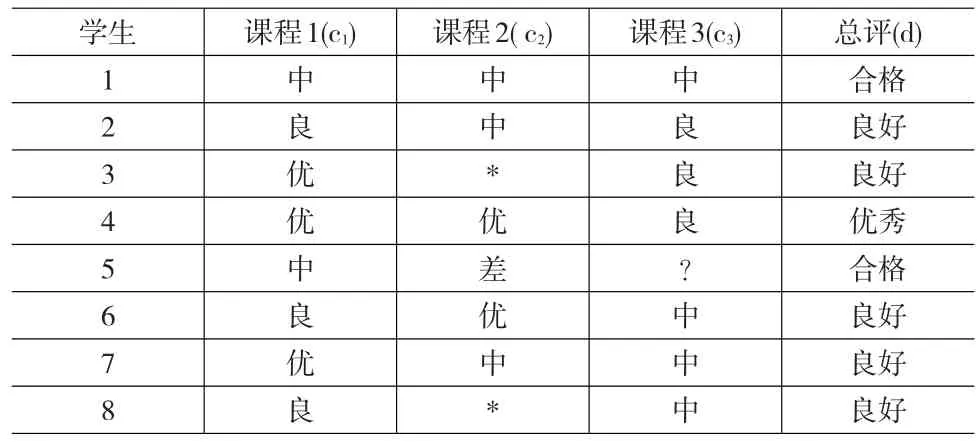
表1 某學校教學管理信息系統中的一個信息表

在表1中，對象全集U={1，2，…，8}；c1，c2和c3是條件屬性，分別表示課程1，2和3；總評d是決策屬性。令P={c1，c2，c3}，VP={優，良，中，差}，優＞良＞中＞差；Vd={優秀，良好，合格}，優秀＞良好＞合格；Cl1={x∈U|f(x，d)=合格}={1，5} ，Cl2={x∈U|f(x，d)=良好}={2，3，6，7，8}，Cl3={x∈U|f(x，d)=優秀}={4}。

利用已有特征優勢關系下的粗糙決策分析方法計算結果如下：

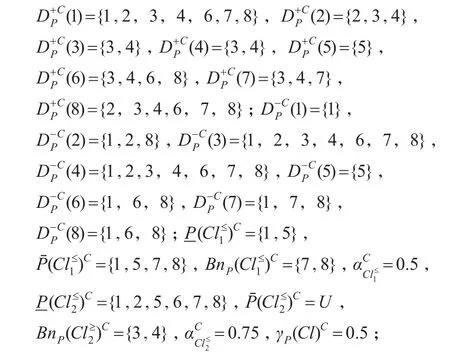
（1）c1≤中∧c2≤中∧c3≤中→d∈Cl1，即學生三門課程的成績至多為中，則學生的綜合評價為合格；

（2）c1≤中∧c2≤差∧c3=？→d∈Cl1，即學生課程1的成績之多為中，課程2的成績為差，課程3的成績為缺席型未知值，則學生的綜合評價為合格；

（5）c1=優∧c2=優∧c3≥良→d∈Cl3，即學生課程1和課程2的成績為優，課程3的成績至少為良，則學生的綜合評價為優秀。

5 結束語

應用粗糙集方法直接在不完備信息系統中獲取決策規則，避免了因完備化信息系統而造成信息丟失的影響，可以較好地解決不完備信息下的多屬性決策問題。本文在同時具有缺席和遺漏型未知屬性值的廣義不完備序決策系統中，提出一種基于新特征優勢關系的粗糙決策分析方法，克服了已有方法在粒度劃分上過于寬松的不足，是已有粗糙決策分析方法的進一步推廣。同時，本模型較好的處理了廣義不完備序決策系統的規則獲取問題，對系統的決策分析提供了一定的決策支持。

[1]Pawlak Z.Rough Sets：Theoretical Aspect s of Reasoning about Data[M].Norwell,Mass,USA：Klumer Acadimic Publishers,1991.

[2]Greco S，Matarazzo B，Slowinski R.Rough Approximation of a Preference Relation by Dominance Relation[J].European Journal of Operation Research,1999,117(1).

[3]Greco S,Matarazzo B,Slowinski R.Rough Sets Theory for Multi-criteria Decision Analysis[J].European Journal of Operational Research,2001,129(1).

[4]Greco S,Matarazzo B,Slowinski R.Generalizing Rough Set theory Through Dominance-based Rough Set Approach[C].Heidelberg：Springer-Verlag,2005.

[5]何亞群,胡壽松.不完全信息的多屬性粗糙決策分析方法[J].系統工程學報,2004,19(2).

[6]Shao M W,Zhang W X.Dominance Relation and Rules in an Incomplete Ordered Information System[J].International Journal of Intelligent Systems,2005,(20).

[7]胡明禮,劉思峰.基于廣義擴展優勢關系的粗糙決策分析方法[J].控制與決策,2007,22(12).

[8]駱公志,楊曉江,周德群.基于限制擴展優勢關系的粗糙決策分析模型[J].系統管理學報,2009,18(4).

[9]Yang X B,Yang J Y,Wu C,et al.Dominance-based Rough Set Approach and Knowledge Reductions in Incomplete Ordered Information System[J].Information Sciences,2008,178(4).

[10]楊習貝,竇慧莉,宋曉寧等.廣義不完備序值系統中的優勢關系粗糙集[J].江蘇科技大學學報(自然科學版),2011,25(3).

[11]Chen H M,Li T R,Ruan D.Maintenance of Approximations in Incomplete Ordered Decision Systems while Attribute Values Coarsening or Refining[J].Knowledge-Based Systems,2012,31.