多元離散-連續比例選擇模型的構建
王 芯,呂曉玲
(中國人民大學a.應用統計研究中心;b.統計學院,北京 100872)
0 引言
傳統的離散選擇模型是指在很多個備選方案中選擇其中的一種[1],而離散-連續選擇模型是傳統的擴展,不僅僅考慮選擇幾個備選方案,還要考慮每個選擇的取值。離散-連續選擇模型可以應用在商品消費,時間分配等問題中。“離散”指從選擇集里面選擇哪些元素(商品、活動等),“連續”是指選擇的元素取值是多少。Kim等2002年提出的KAR模型以及Bhat 2005年提出的MDCEV模型在消費者行為和時間分配的研究中有著廣泛的應用[2,3]。這兩個模型在形式上比較接近,都是基于Wales和Woodland 1983年提出的Kuhn-Tucker模型[4],只是對誤差項的假設有所不同。KAR和MDCEV模型的形式容易理解,模型滿足經濟學中對效用和邊際效用的定義,并且參數有比較直接的意義,但是這兩個模型都是以絕對時間或者數量為研究對象,如果應用在比例數據中效果會比較差。而傳統的研究比例數據的Amemyia-Tobin模型[5]在參數估計過程中需要用到高維的積分,估計起來比較困難。本文基于KAR和MDCEV模型的建立模式,提出適合比例數據的效用函數,建立新的適合比例數據的模型。模型形式比較簡單,具有經濟學上的意義,并且估計起來比較簡單。
1 模型回顧
KAR模型是在消費者行為研究背景下提出的,假設有M個商品,則購買商品的總效用是:

其中xj對商品的購買數量,并且滿足預算限制p′x=E,p 是商品的價格,E 是總預算。 ψj,αj,γj是參數。γj使得模型可以存在角解,也就是通過無差異曲線和預算線得到的最優解中某些商品的取值可以為0。ψj>0稱為基準效用參數,該值越大,表明消費者越傾向于購買這個商品。0<αj<1稱作飽和度參數,當αj比較小的時候,該商品的邊際效用就會減小的比較快,那么消費者就會傾向于較少的購買該商品。相反,如果αj接近于1,那么邊際效用就會減小的比較慢,消費這就會傾向于較多的購買該商品。
在KAR模型中,為了保證邊際效用為正,在邊際效用中引入了對數正態分布作為誤差項,如下所示:

為了考慮消費者的異質性,可在基準效用參數中引入協變量x,即假定ψj(x)=exp(β′x)。
MDCEV是在時間分配的背景下提出來的,這時條件限制中的權重都是相等的,即p1=…=pM。該模型的效用函數與KAR模型類似,只是假定誤差項的分布是標準極值分布,則似然函數為:
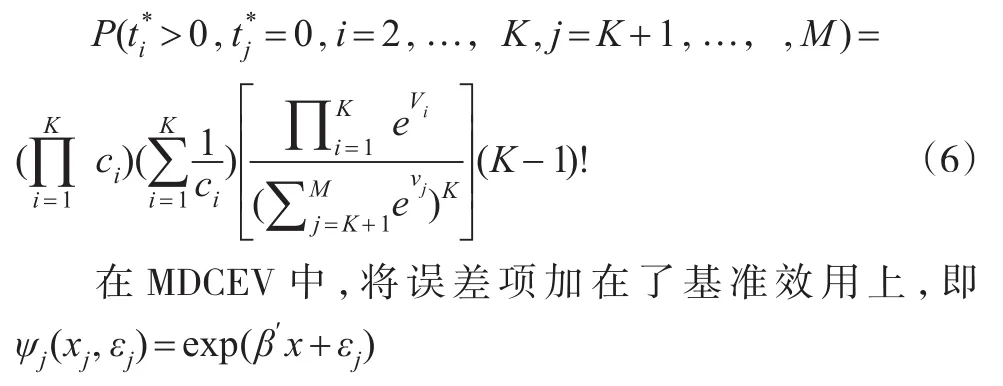
其中xj表示的是第 j個活動的屬性。
2 比例模型
2.1 效用函數形式
在消費者行為研究中,比例數據Pk(k=1,…K)是每個商品消費金額占總金額的比例;在時間分配問題中,是指每個活動的時間占總時間的比例,這時可以簡單的考慮總效用是各個比例的函數。簡單的使用KAR模型或者MDCEV模型去分析這個問題是存在問題的,所以在這里提出了新的比例模型。本文在時間分配的背景下去討論模型的相關問題,模型很容易可以拓展到商品消費的情況。新的效用函數如下:

第k活動的邊際效用是ψk(1-pk)αk,ψk表示的基準邊際效用。當 pk等于0時,邊際效用是ψk,是邊際效用最大的時候。對于兩個活動i和 j,如果活動i所對應的參數ψi大于活動 j所對應的參數ψj,那么活動i的角點解會比活動 j的少。參數αk的作用是隨著第k個活動的增加減少邊際效用,使得邊際效用滿足邊際遞減的規律。如果活動i所對應的參數αi大于活動 j所對應的參數αj,那么活動i的平均時間比例會小于活動 j的平均時間比例。
2.2 帶誤差項的效用函數
在式(7)的基礎上可以在效用模型上加上隨機誤差項,則總效用函數為:
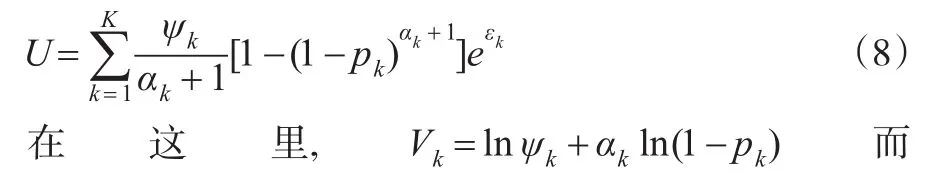

其中 hj=V1-Vj,vj=εj-ε1,j=2,…,,M,φ(·)是多元正態分布的密度函數,Ω是協方差矩陣。J是雅克比行列式。
對于誤差項分布的假設,可以首先嘗試兩種誤差項分布的假設,然后選擇似然函數值比較大的做為參數估計的結果。
在實際數據分析中,該模型有一個局限,就是只能分析至少選擇了兩個活動的數據。
2.3 異質性
在參數中加入社會人口學變量,將參數再參數化,進而分析不同變量對時間分配的影響。基準邊際效用參數和飽和參數的再參數化如下所示:
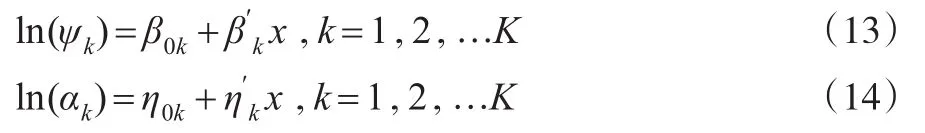
其中 x 是個體的社會人口學變量,β0k,βk,η0k,ηk是對活動k的參數。在實際的估計中,會有參數可識別的問題(Train,2009),所以需要在參數估計時做出假定。本文在不考慮異質性時假設ψ1=1,在考慮異質性時假設β01=β′k=0。
3 實際數據分析
實際數據是在北京和香港地區進行的關于筆記本購買情況的調查數據。通過電話調查的方式對北京和香港的居民進行調查,調查的對象是曾經購買過筆記本的人群。主要了解被調查者在購買筆記本的過程中,信息搜索的時間分配情況,調查的信息搜索渠道包括:網絡、實體店、廣告和親友。考慮的協變量包括性別、年齡、教育程度、每天平均上網時間、是否為第一次購買筆記本這些變量、居住地。由于模型的局限,此處只考慮至少選擇了兩個途徑的那部分受訪者,有效樣本量為233,用MAD[6]方法剔除異常值,樣本量為214,其中北京為109個,香港為105個。四個途徑的基本描述分析如表1所示。
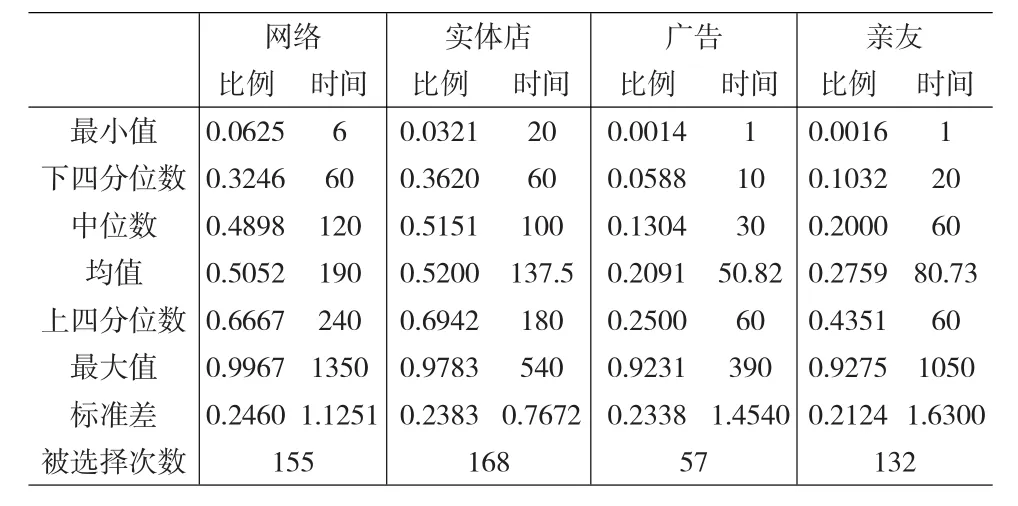
表1 北京和香港地區消費者購買筆記本信息搜索各渠道時間分配數據的描述分析
從表1可以看出實體店、網絡和親友被選擇的次數較多。絕對時間和比例時間呈現出不同的特點,網絡的絕對時間是最大的,而實體店的時間比例是最大的。親友的絕對時間離散程度比較大,但是時間比例的離散程度不是很大。
本文對比例數據和絕對時間數據同時進行了分析。分別嘗試了誤差項為標準正態分布和標準極值分布的形式,此處僅給出擬合效果較好的標準極值分布的結果。分別將基準邊際效用參數和飽和參數加入協變量,使用向后選擇變量的方法,剔除不顯著的變量,具體參數估計結果如表2所示。
從表2可以看出,比例數據的參數估計結果和絕對時間很相似,這是因為兩個模型中對基準邊際效用都是反應每個途徑被選擇的次數大小的。在協變量相同的條件下,實體店(ψ2)被選擇的次數會比網絡的多,而廣告(ψ3)被選擇的次數比較小。年齡比較大的人會更加傾向于不選擇網絡。教育程度比較高的人會相對比較少的選擇親友。平均上網時間比較長的人會較少的選擇實體店和親友(ψ4),較多的選擇網絡。第一次購買的人會比不是第一次購買的人更傾向于選擇親友獲取信息。而居住地在香港的人會比居住地在北京人較少的使用實體店這個渠道進行信息搜索。從飽和參數的估計結果來看,網絡(α1)和實體店(α2)的平均時間比例比廣告(α3)和親友(α4)大。
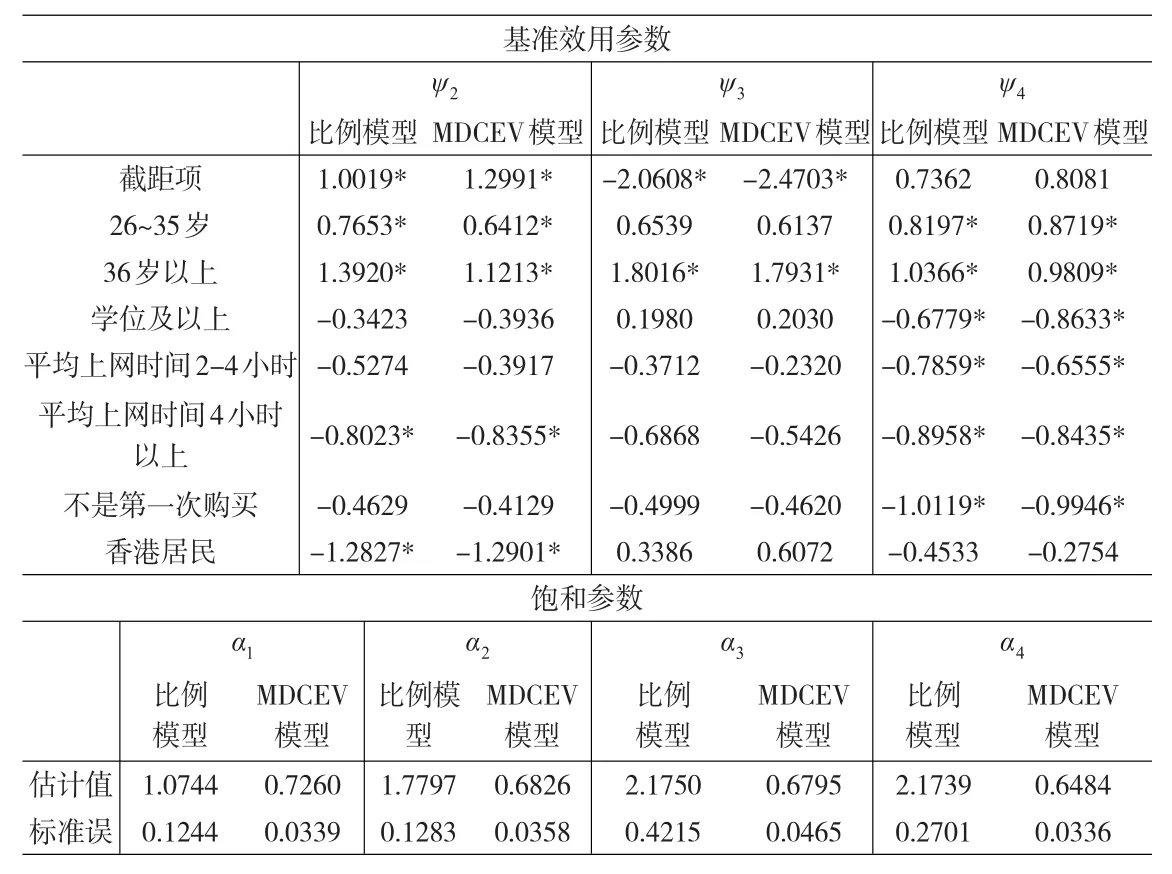
表2 假定基準效用參數具有異質性的模型估計結果
在飽和參數中加入協變量,基準邊際效用參數中不加入協變量,結果如表3所示。可以看出年齡和是否為第一次購買會對比例數據的飽和參數有影響。在選擇途徑數大于1個的人群中,年齡在36歲及以上的人使用網絡的時間比例會比36歲以下的人少,而使用實體店的時間比例則比其他年齡段的人群大。對于廣告來說,年齡越大的人,使用的時間比例會越大。而咨詢親友的時間比例在各個年齡段沒有顯著的差別。除此之外,第一次購買的人會分配相對來說更多的時間比例咨詢親友。而對絕對數據的飽和參數有顯著影響的變量包括年齡和居住地,這和比例模型中的結果有所不同。年齡在36歲以上的人花費在網絡上的絕對時間比36歲以下的人要少,而年齡越大的人會傾向于花費較多的時間在廣告上面,這與比例模型中的估計結果是一致的。但是在比例模型中36歲以上的人在獲取信息的過程中,實體店的時間比例會比其他年齡段的人大,而在絕對時間里面沒有體現這一特點。除此之外,是否第一次購買對時間比例的分配有影響,但是對絕對時間的分配沒有影響,也就是說無論是否為第一次購買,如果咨詢親友的意見,他們花費的絕對時間是類似的,但是第一次購買的人咨詢親友的時間占全部時間的比例會更大一些。還有居住地對時間比例沒有影響,但是對絕對時間有所影響,香港居民會傾向于花費較少的時間通過實體店進行信息搜索。
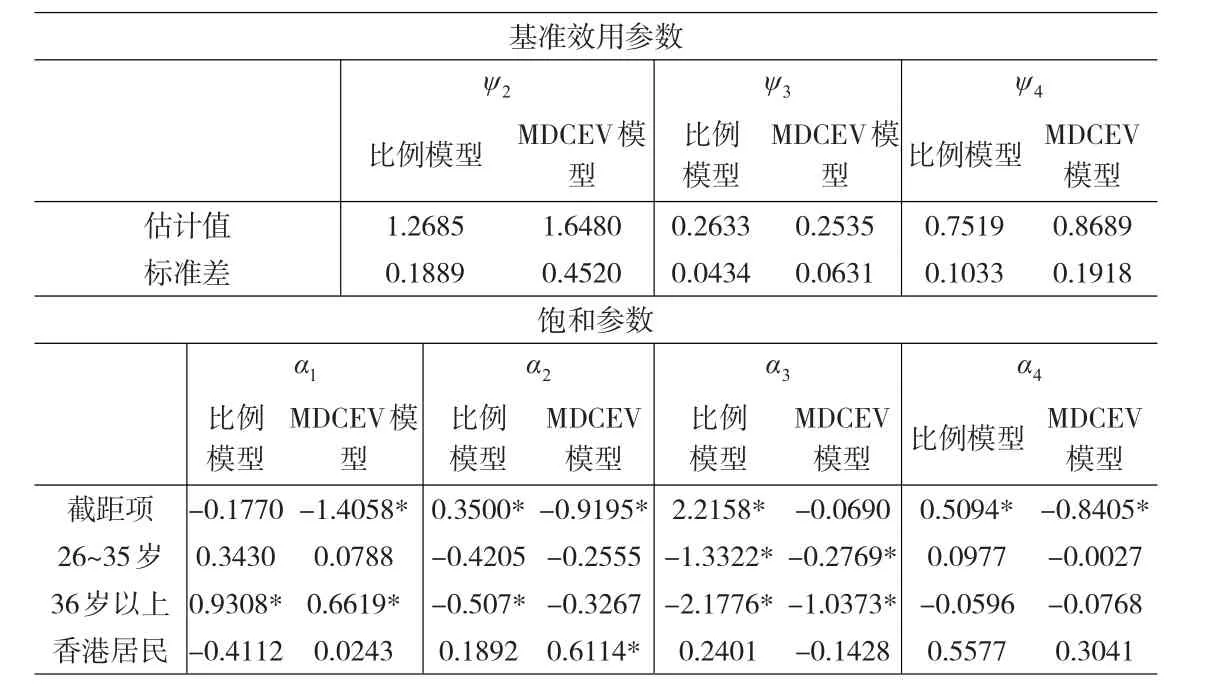
表3 假定飽和度參數具有異質性的模型估計結果
4 結論
本文提出了適合比例數據的離散-連續選擇模型。模型的構建過程參考了KAR模型和MDCEV模型的效用函數形式,新的效用函數是仍然是非線性、可加的形式,可以保證邊際效用為正。在所有活動的比例和為1的限制條件下,利用K-T條件得到似然函數,進而進行參數估計。本文同時使用比例模型以及MDCEV模型分析了北京和香港兩的消費者購買筆記本時在各渠道信息搜索的時間分配數據,從兩個不同的角度看出人群的不同特點。
該比例模型有一個局限就是只能應用于至少選擇了兩個活動或者商品的數據中。在今后的研究中,會基于現有的比例模型的思想,構建可以包含只進行一個活動這種數據的效用函數形式。或者考慮混合模型,用新的效用函數表示未包含進去的這部分數據,進而可以分析全部人的行為特點。
[1]Train K E.Discrete Choice Methods with Simulation(2ndEdition).[M].New York:Cambridge University Press,2009.
[2]Kim J,Allenby G M,Rossi P E.Modeling Consumer Demand for Variety[J].Marketing Science,2002,21(3).
[3]Bhat C R.A Multiple Discrete-continuous Extreme Value Model:Formulation and Application to Discretionary Time-use Decisions[J].Transportation Research Part B,2005,39(8).
[4]Wales T J,Woodland A D.Estimation of Consumer Demand Systems with Binding Non-negativity Constraints[J].Journal of Econometrics,1983,21(3).
[5]Yen S T,Lin B H,Smallwood D M.Quasi-and Simulated-Likelihood Approaches to Censored Demand Systems:Food Consumption by Food Stamp Recipients in the United States[J].American Journal of Agricultural Economics,2003,85(2).
[6]Hampel F R.The Breakdown Points of the Mean Combined with Some Rejection Rules[J].Technometrics,1985,27(2).

