基于測量系統量值特性的不確定度評定研究

陳育蕾

(1.中國計量學院，杭州310034；2.浙江省哲學社會科學重點研究基地、浙江省標準化與知識產權管理人文社科重點研究基地，杭州 310034)

在不同測量過程中，根據研究目的、側重點及測量系統組成因素的不同，每個測量系統不確定度來源會有所差異，但測量系統也具有共性的方面。因此，美國三大汽車公司通用、福特和克萊斯勒等聯合推行測量系統分析，提出了測量系統評定的5個量值指標即偏移、重復性、復現性、穩定性和線性等。這5個量值特性不僅反映了不確定度的基本特征，也可以作為測量系統的不確定度主要來源。按照JJF1059.1-2012技術規范，選擇5個量值指標的測量不確定評定的適合方法，分別計算不確定度分量，按照不確定度合成方法獲得測量系統的總不確定度，并完成不確定度報告。這樣做使不確定評定結果更準確，不確定度來源分析更全面，且比以往的方法更簡單直觀[1～3]。

1 測量系統量值特性分析方法的測量模型[4,5]

被測量的某個特性的測得的量值記為Y，零件的約定量值為x，真實值在實際測量中無法得到，誤差記為ε。那么：

假設被測量和測量者之間不存在交互作用或交互作用接近0，這意味著測量者對所有被測量是相同的，該模型稱為可疊加模型。實際上疊加性假定不總是都成立，但是實際應用中交互作用引起的不確定度較小，可以將其忽略[6]。

因此，將5個量值特性指標表示的誤差方法改換為測量系統不確定度評定，也就是把式（3）改成：

其中U是總不確定度，u是合成標準不確定度，k是包含因子。

2 測量系統不確定度評定[2,7]

2.1 偏移引起的不確定度評定

偏移是系統測量誤差的估算值。對于測量次數是n，此樣本的約定量值x0，測得值為xi，其中i從1到n。觀測平均值：

由上可知：偏移b引起的不確定度u1包括，樣本平均值xˉ所引起的不確定度u11，另一個是約定量值x0引起的不確定度u12。測量平均值引起的不確定度為u11，屬于A類評定。其計算公式如下：

2.2 重復性和復現性引起的測量不確定度評定

重復性測量條件是指相同操作者、測量程序、測量系統、操作條件和地點，并在短時間內對同一或相類似被測對象重復測量的條件下進行。復現性測量條件是指在不同測量系統、不同地點、不同操作者、對同一或相類似對象重復測量的一組測量條件。

2.2.1 測量系統重復性與復現性研究采用均值—極差法[1,8]

均值-極差分析法用于正態分布的前提下，估計單次測量結果試驗標準偏差s的一種方法，屬于不確定度的A類評定。在重復條件下，對觀察對象進行測量（重復測量次數少于10次為一組），分別測量了m組，每組的重復次數相同，都為n次，測量結果xij（i從1到n，j從1到m），則通過每一組的極差Rj=maxxij-minxij的平均值：

其中，C為極差系數可以查表獲得。

我們結合檢測實驗室的相關數據來了解均值極差法的步驟。數據來源于參考文獻[8]，該測試過程是以二等環規標準作基準，對內徑式樣進行測試。數據情況見表1。

表1 數據情況

第一步在利用均值—極差法來分析測量系統時，首先要修正可預見方式變化的測量誤差分量即系統誤差，該測量系統假定系統誤差已被修正。第二步要判斷被測者和測量者之間是否有交互作用。即每位測量者對每個被測者各重復測量2次，計算均值，三個測量者得到30個均值，將每個測量者的10個均值點連成一條線。這3條線幾乎平行，認為零件和測量者之間無交互作用。無交互作用才可以進行第三步計算，如測量結果又交互作用，先進行數據轉換和處理。第三求重復性產生的變差，可以求得：

2.2.2 貝塞爾公式法求重復性和復現性所引起的不確定度

重復性引起的不確定度分量，可用貝塞爾（Bessel）公式法來計算。當以單次數據作為測得值時，測量重復性單次測量的標準差。以多次測量平均值作為測量結果時，重復性則為平均值的標準差。

xi為第i次測量的測得值，xˉ為n次測量所得一組測得值的算術平均值，n為測量次數。

一般設測量儀器的工作范圍為：0～1，選擇能夠覆蓋整個量程的零件m個，通過高精度測量設備測量每個零件的約定量值為：x0j（j從1到m）

對m個零件進行n次測量，測量結果為 xij（i從1到n），計算每個零件的平均值為：

其中d2為極差法求標準差的系數，是個測量次數有關的常數，可查表獲得。

2.3 穩定性引起的不確定度評定

穩定性是指儀器保持其計量特性隨時間恒定的能力。通常穩定性是指測量儀器的計量特性隨時間不變化的能力。但隨著時間的變化，由于這些影響因素都未發生改變，它們對穩定性的影響因此也基本未改變。對于系統穩定性導致的不確定度采用B類評定，假設某測量系統進行定時監控，獲得其穩定度的范圍是：±a，是均勻分布，一般情況下，穩定性的影響不會超過a。即穩定性導致的不確定度分量是：

自由度為：∞。

2.4 線性引起的不確定度評定[7]

在測量周期內，測量儀器的量程內選擇零件，最佳擬合偏移與約定量值，所得直線的斜率乘以零件的過程變差的指數[7]。即指量與量之間按比例、成直線的關系。

一般設測量儀器的工作范圍為：0～1，選擇能夠覆蓋整個量程的零件m個，通過高精度測量設備測量每個零件的約定量值為：x0j（j從1到m）

對m個零件進行n次測量，測量結果為 xij（i從1到n），計算每個零件的平均值為：

2.5 測量系統合成標準不確定度

根據JJF1059.1-2012中測量不確定度合成可知：線性與偏移雖是測量系統2個不同的量值特性指標，但對于測量結果的影響卻是相同的。假設在全量程范圍內各點的偏移均被修正，實際上也就不存在線性引起的不確定度（可參考線性的定義）。因此，進行測量不確定評定時，這2個分量可以看為一個分量，一般由最大偏移來確定。根據不確定度原理及以上的分析，測量系統合成標準不確定度[7]：

3 實例

某車間要對某零件進行不確定度評定。選定一個零件，甲乙丙三個測量者，對每個零件測量20次，所得數據如表2所示，遵照線性分析方法，選定5個零件，一個測量者，對每個零件測量10次，所得數據如表3所示。

表2 測量者甲、乙、丙進行等精度測量的數據

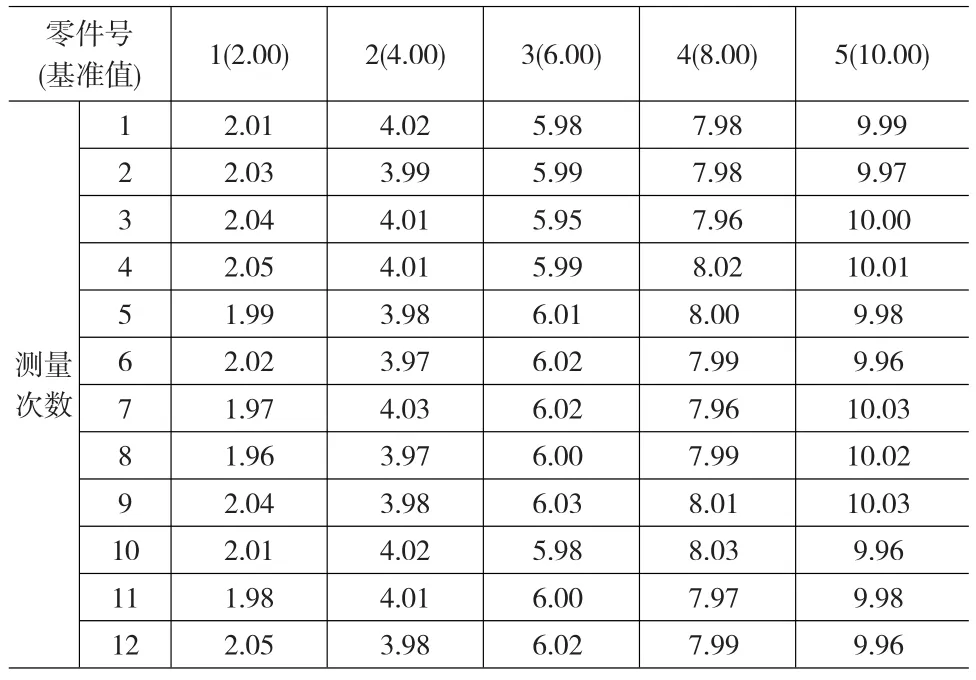
表3 線性度測量數據表

第一步：偏移和線性引起的不確定度分量u1（由2.5可知）

每個測量點的偏移值分別為：-0.0125、0.0025、0.0008、0.01、0.0092，那么：

第二步：重復性引起的不確定度分量u2

由重復性引起的不確定度分量用貝塞爾公式法，應由測量者甲的測量次數來確定：

第四步：穩定性引起的不確定度分量u4

對測量系統進行為期12個小時的觀測，結果發現其偏移機會為0。由于分辨力的原因，對于更細微的變化系統無法測出，因此存在舍入誤差。根據誤差舍入原則，穩定性的范圍±a為±0.0005v。根據均勻分布得穩定性引起的不確定度分量為：

第八步：不確定度報告

環境溫度等環境條件符合各項規程，系統誤差被認為基本被修正。則不確定度為：

U95=0.04947V(包含概率為：95%，包含因子：k=1.96，自由度：veff=362.14196)

[1]JJF1001-2011、JJF1059.1-2012、JJG124-2005技術規范.

[2]薛慶文，孫中泉，張華鋒.基于量值特性的ATS動態測量不確定度評定[J].國外電子測量技術，2010,7(29).

[3]謝少鋒，陳曉懷.測量系統不確定度分析及其動態性研究[J].計量學報，2002,7（23）.

[4]Wendle T.Measurement uncertainty[J].Quality Today,2004,6.

[5]Grabe M.Estimation of measurement uncertainty-an alternative to the ISO Guide[J].Metrologia,2001,38(2).

[6]宋明順,陳意華等.測量不確定度評定中忽略相關項所帶來的風險評估[J].A計量學報，2005，26(1).

[7]唐燕杰，陳曉環等.測量系統不確定度研究[J].儀器儀表用戶，2003，10(3).

[8]鄭曉云，張娟娟，李平.均值極差法在質量控制中的應用[J].機械工業標準化與質量，2003，4(8).