從一道哈佛試題淺談因數(shù)構形*

☉福建省廈門第一中學 王淼生

從一道哈佛試題淺談因數(shù)構形*

☉福建省廈門第一中學 王淼生

一、著名學府入學試題

世界上最著名的哈佛大學曾有這樣一道入學試題，原題如下：

請在下列一組圖形符號中找出它們所蘊含的內(nèi)在規(guī)律，然后在圖形空白處填上恰當?shù)膱D形.

剖析：先觀察上述所給六個圖形，第一個與第四個圖形好像都是大寫英文字母“M”，只是橫線的位置不同而已；第二個圖形酷似“心”形；第三個圖形似乎“8”字形；第五個圖形恰為橫桿下面掛一個鋼圈；最后一個即第七個圖形是倒置的等腰三角形.僅僅從單個圖形看很難有所突破，必須將這些圖形綜合在一起全面考慮，因此需要進一步深入研究圖形.

所謂尋找規(guī)律，就是尋求共同屬性，也就是從上述六個具體的圖形中抽象出本質(zhì)的特征.抽象就是從眾多事物中提取共同、本質(zhì)特征，舍棄個別、非本質(zhì)特征.要抽象就必須進行比較，沒有比較就無法找到本質(zhì)上共同的部分.共同特征是指那些能把一類事物與他類事物區(qū)分開來的特征，這些具有區(qū)分作用的特征即為本質(zhì)屬性，因此抽取事物的共同特征就是提煉事物的本質(zhì)屬性，舍棄非本質(zhì)的特征，就是去粗取精、去偽存真、由表及里的過程.

盡管上述六個圖形各不相同，似乎毫無關聯(lián)，但是有一個共同特征：都是軸對稱圖形！既然都是軸對稱圖形，從數(shù)學視角只要關注每一個圖形右邊的一半，因此我們用不透明的紙板把上述每個圖形對稱軸左邊的圖形遮住，此時再來觀察這些圖形，就容易發(fā)現(xiàn)這些圖形蘊含的規(guī)律是阿拉伯數(shù)字1、2、3、4、5、7，中間缺少一個數(shù)字6，因此只要在第六個位置的橫線上方的空白處畫出圖形是數(shù)字“6”的特征圖形，然后運用軸對稱的性質(zhì)畫出左邊對應的圖形并組合于一體即可（詳見文1）.

傲視全球的哈佛大學居然把看似如此簡單的問題作為入學考題，簡直讓人不可思議！從一個側(cè)面反映了美國等發(fā)達國家的數(shù)學教育何等重視數(shù)形結(jié)合思想的滲透與考查.遺憾的是我國數(shù)學教育在數(shù)學思想方面顯得較為薄弱，時至今日，盡管我國新一輪課改實施十余年，盡管新課標教材明顯提高了對數(shù)學思想方法的要求，但是不少教師依然抱著“冷戰(zhàn)思維：題海戰(zhàn)術”，依然還是老一套：一個概念、三個注意，外加無休止的所謂強化訓練，依然還是帶著極端功利的思想：重數(shù)量、重知識、重方法、重結(jié)果而輕質(zhì)量、輕能力、輕過程、輕思想.

二、數(shù)形結(jié)合思想

恩格斯指出：“數(shù)學是研究現(xiàn)實世界的量的關系與空間形式的科學.”數(shù)學的研究對象是數(shù)量關系和空間形式，“數(shù)”與“形”有著十分密切的聯(lián)系，可以說宇宙間萬物幾乎都融入“數(shù)”與“形”的矛盾統(tǒng)一體之中.正因為如此，數(shù)形結(jié)合思想幾乎無處不在、無時不在.

正是基于對數(shù)與形的深入研究才產(chǎn)生數(shù)學這門學科，從而讓人們從不同的側(cè)面來認識事物，進而把對數(shù)量關系的研究轉(zhuǎn)化為對圖形性質(zhì)的研究，或者把對圖形性質(zhì)的研究轉(zhuǎn)化為對數(shù)量關系的研究.這種解決問題過程中的“數(shù)”與“形”不斷地相互轉(zhuǎn)化的研究策略，就是數(shù)形結(jié)合思想的具體體現(xiàn).數(shù)形結(jié)合思想是一種極其重要的數(shù)學思想，數(shù)形結(jié)合使得抽象的數(shù)學語言與直觀的幾何圖形有機結(jié)合起來，使得抽象思維與形象思維融為一體.

數(shù)形結(jié)合就是根據(jù)數(shù)學問題的條件和結(jié)論之間的內(nèi)在聯(lián)系，既要分析其代數(shù)意義，又要揭示其幾何直觀背景，充分利用數(shù)與形的關系，尋找解題思路，使問題化難為易、化繁為簡，從而達到解決問題的目的.數(shù)形結(jié)合既是一種重要的數(shù)學思想又是一種重要的數(shù)學方法，包含“以形助數(shù)”和“以數(shù)構形”兩個方面.借助形的直觀性來闡明數(shù)量之間的關系，即以形為手段，以數(shù)為目的；或者借助于數(shù)的精確性和嚴密性來闡明形的某些屬性，即以數(shù)為手段，以形為目的.運用數(shù)形結(jié)合，由“形”到“數(shù)”轉(zhuǎn)化往往明顯，而由“數(shù)”構“形”則需要強烈的轉(zhuǎn)換意識及敏銳的構造能力，因此，數(shù)形結(jié)合思想關鍵在于側(cè)重從“數(shù)”到“形”的轉(zhuǎn)化，通俗地說就是依據(jù)數(shù)的特征來構造幾何圖形.

值得注意的是：絕大多數(shù)人認為這個“數(shù)”就是狹義的數(shù)，其實這個數(shù)是一個廣義的數(shù)，即可以是純粹的數(shù)字，還可以是式子（包括方程、不等式等），甚至可以是數(shù)學問題（包括生活問題），本文擬從幾個實例來闡述由數(shù)如何構造最簡單、最熟悉的平面幾何圖形（線、三角形等）、立體幾何圖形（三棱錐、長方體等）、平面解析幾何圖形（圓、橢圓等）及空間解析幾何圖形（平面、球等）.

三、由數(shù)構形的策略

1.由數(shù)（數(shù)字、代數(shù)式）構造平面幾何圖形模型

平面幾何中最簡單的圖形就是直線（包括射線、線段）、三角形.有些數(shù)學問題看似是純代數(shù)問題，若從代數(shù)方面入手則十分復雜，如果注意觀察數(shù)量關系、觀察外形結(jié)構、觀察所求結(jié)論，然后對已知條件及所求結(jié)論深入剖析會發(fā)現(xiàn)：這些表面上的代數(shù)問題其實與幾何圖形密不可分，于是構造幾何圖形，往往會得到意想不到的收獲.

剖析：上述求和代數(shù)式中的分式分別表示1的一半、一半的一半、…，這不正是“一尺之棰，日取其半，萬世不竭”的再現(xiàn)嗎？據(jù)此構造AB=1的一條線段（即一尺之棰），取AB的中點A1，再取線段A1B的中點A2，再取線段A2B的中點A3（日取其半），如此不斷反復取下去（萬世不所有這些線段長度之和為1，即：

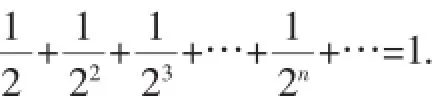
評注：案例1是2008年廣東省高考試題，所求和的代數(shù)式表明是一個無窮級數(shù)求和，而且是無窮等比遞減數(shù)列，因此利用極限思想構造線段，讓人賞心悅目，這正是數(shù)形結(jié)合的魅力所在！當然，本題還可以構造面積為1的正方形，然后將這個正方形不斷反復對折下去即可.

2.因數(shù)（不等式、實際問題）構造立體幾何圖形模型

立體幾何中最簡單的幾何圖形就是長方體及三棱錐等，妥善構造這些幾何體，并利用這些幾何體本身具有的代數(shù)性質(zhì)（尤其是長方體的幾何與代數(shù)性質(zhì)！），達到四兩撥千斤的奇效.

案例2：世界上任何6個人中，總可以找到3個相互認識的人或者3個互相不認識的人.

剖析：我們把6個人看作6個頂點，互相認識的2個人對應的頂點連成紅線，否則連成藍線，那么本問題就等價于在6個頂點中的每2個點之間用紅線或者藍線相連，則至少存在一個同色三角形.

我們?nèi)稳∫粋€頂點為A，則A與其余5個頂點的連線共有5條線，由于只有紅與藍兩色，依據(jù)抽屜原理可得至少存在3條線是同色，不妨設AB、AC、AD同是紅色，此時構造三棱錐A－BCD，下面我們來考察△BCD，若BC、CD、DB三線中至少有一條紅色線，不妨設BC，則含有一個紅色三角形，即△ABC是紅色三角形，即存在一個同色三角形，否則△BCD就是藍色三角形，至此本問題得以解決.也就是說：世界上任何6個人中，必有3個人或者相互認識或者互不認識！多么不可思議的命題，卻是千真萬確的真理！

案例3：若α、β、γ均為銳角，且sin2α+sin2β+sin2γ=1，證明：

剖析：注意到已知條件：三銳角正弦的平方和等于1，這不正是長方體一個重要的代數(shù)性質(zhì)嗎？即長方體的體對角線與共點的三個面所成的角α、β、γ的正弦的平方和等于1，因此構造長、寬、高分別為a、b、c的長方體，將復雜的三角問題順利轉(zhuǎn)化為不等式問題，因此所求證的原不等式等價于：

利用基本不等式：a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ca，則只要證明：

不妨令abc=1，則上式等價于：

上式正是調(diào)和平均數(shù)與算術平均數(shù)之間的關系.

評注：匈牙利數(shù)學家羅莎指出：“解決數(shù)學問題時往往不是對問題實行正面攻擊，而是不斷地將它構造、變形，直至把它轉(zhuǎn)化成能夠得到解決的問題.”上述由數(shù)構形，再由形輔數(shù)的策略，正是羅莎名言的最佳詮釋與踐行.

案例2是1947年匈牙利數(shù)學奧林匹克競賽試題，它僅僅是著名的拉姆賽定理的一個特例.拉姆賽定理：設空間6個點中任意4點不共面，若將其中兩點間的連線染成紅色或者藍色之一，則必然存在一個三邊顏色相同的三角形.

案例3為2005年咸陽市教師技能大賽壓軸題，因求證結(jié)論極其復雜，原解答直接從三角化簡、變形入手，顯得特別復雜、冗長，通過構造長方體可獲得妙不可言的解答.

3.因數(shù)（代數(shù)式）構造平面解析幾何圖形模型

解析幾何本身就是數(shù)形結(jié)合的產(chǎn)物，這正是解析幾何的精髓所在.解析幾何中最簡單的幾何圖形就是圓、橢圓、雙曲線及拋物線等，由圓錐曲線（包括圓）的定義可知圓錐曲線具有鮮明的特征，抓住其本質(zhì)特征，往往可找到構造圓錐曲線的入口，并妥善利用圓錐曲線的定義、性質(zhì)迅速解決問題.

案例4：已知α、β為銳角，且sin（α+β）=2sinα.證明β＞α.

剖析：構造直徑AB=1的圓，在AB的上方、下方的圓弧上分別取點C、D，使∠CAB=α，∠DAB=β，則BC=sinα，BD=sinβ，由正弦定理得CD=sin（α+β）.

在△BCD中，顯然BD＞CD-CB，則有sinβ＞sin（α+β）-sinα?sinβ＞2sinα-sinα=sinα?β＞α.

評注：一般來說，代數(shù)問題較為抽象，若能通過構造恰當?shù)膸缀螆D形，將數(shù)量關系轉(zhuǎn)化為幾何關系，利用熟悉的數(shù)形結(jié)合這一重要的數(shù)學思想方法，往往可以增加問題的直觀性，使得解答過程事半功倍、解答流程獨具匠心.倘若純粹從三角的放縮來解決案例4顯得非常復雜，而構造圓則迅速獲解.由此不難看出：要想構造解析幾何圖形，必須熟悉數(shù)或代數(shù)式所代表的幾何意義，同時還要掌握幾何圖形的代數(shù)結(jié)構，將兩者有機結(jié)合，才是由數(shù)構形的關鍵所在.

4.因數(shù)（方程、方程組等）構造空間解析幾何圖形模型

顯然，d＞r?平面與球相離?方程組無實數(shù)解；d＜r?平面與球相交?方程組有無數(shù)多組實數(shù)解，這無數(shù)多組實數(shù)解正是平面截球面所得到的圓上的所有點；d=r?平面與球相切?方程組有唯一一組實數(shù)解.

案例5：試求下列三個方程所組成的方程組所有實數(shù)解：

x+y+z=3，x2+y2+z2=3，x3+y3+z3=3.

剖析：將前面兩個方程分別看作平面與球面，依據(jù)點到平面的距離公式易得d=r，即平面與球面相切，即有唯一一組實數(shù)解，易得x=y=z=1，顯然滿足第三個方程，故該方程組所有的實數(shù)解只有一組，即x=y=z=1.

評注：華羅庚指出：“數(shù)形本是兩相依，焉能分作兩邊飛.數(shù)缺形時少直觀，形缺數(shù)時難入微.切莫忘，幾何代數(shù)統(tǒng)一體，永遠聯(lián)系莫分離.”案例5是第2屆美國數(shù)學奧林匹克競賽試題，若直接解方程，撇開計算復雜不說，縱使解出也是索然無味.將它們看作平面與球，借助球心到平面的距離公式獲得心曠神怡的解答！

（說明：因本文涉及圖形較簡單，限于篇幅，略去圖形）

四、一點感悟

筆者在高中數(shù)學教學的同時一直從事奧林匹克競賽輔導，也許因為工作需要，筆者從1990年左右開始關注數(shù)形結(jié)合，尤其對因數(shù)構形問題感興趣.構造法是數(shù)學解題中一種富有創(chuàng)造性的思維方法，體現(xiàn)了數(shù)學思維的創(chuàng)造性.構造法對優(yōu)化思維品質(zhì)、激發(fā)創(chuàng)造力大有裨益，它是數(shù)學思想方法的一朵奇葩，充滿著創(chuàng)造的智慧與優(yōu)美，讓人享受到數(shù)學之美.

由數(shù)構形往往獲得新穎、獨特、簡捷的思維與解法，常常讓人豁然開朗、茅塞頓開，身心得到一種極度的快感與滿足.通過情感態(tài)度與價值有機結(jié)合，優(yōu)化思維品質(zhì)，發(fā)展智力，激發(fā)創(chuàng)新意識、創(chuàng)新精神，提高學生的創(chuàng)新能力，培養(yǎng)創(chuàng)造型人才.

由數(shù)思形、依數(shù)構形需要扎實的基礎知識、厚實的數(shù)學功底、敏銳的觀察能力、豐富的聯(lián)想能力、較強的數(shù)據(jù)處理能力、較高的代數(shù)變形技巧、靈活的遷移能力、強烈的構造意識.誠然，由數(shù)構形、依數(shù)構形絕非一朝一夕，需要長期磨煉，日積月累，做用心之人（多留意）、用眼之人（多閱讀）、用腦之人（多思考），功到自然成.

1.于志洪.一道哈佛入學試題趣賞［J］.數(shù)學通訊（下），2013（12）.

2.沈文選，楊清桃.數(shù)學思想領悟［M］.哈爾濱：哈爾濱工業(yè)大學出版社，2008.

3.王連笑.數(shù)學解題靠數(shù)學思想給力［M］.哈爾濱：哈爾濱工業(yè)大學出版社，2011.

4.王淼生.構造長方體巧證不等式［J］.數(shù)學通訊（下），2012（5）.

5.王淼生.妙用三角形基本性質(zhì)巧解競賽試題［J］.中學數(shù)學（上），2013（3）.A

*本文系全國教育科學規(guī)劃教育部重點課題（立項批準號GOA107017）“小學生數(shù)感的發(fā)展與特征研究及課程設計”；福建省“十二五”規(guī)劃2013年度課題（立項批準號：FJJKXB13—083）“優(yōu)化學生思維品質(zhì)的魅力數(shù)學課堂模式研究”及廈門市2013年第三批課改課題（立項批準號：Z3042）“數(shù)學構造思想方法優(yōu)化學生思維品質(zhì)的實踐研究”的階段性成果.