一道試題的分析與思考
☉江蘇省海門中學 曹亞東
一道試題的分析與思考
☉江蘇省海門中學 曹亞東
一、考題
(本題滿分16分)如圖1所示,公路AM、AN圍成的是一塊頂角為α的角形耕地,其中tanα=-2.在該塊土地中P處有一小型建筑,經測量,它到公路AM、AN的距離分別為3km、km.現要過點P修建一條直線公路BC,將三條公路圍成的區域ABC建成一個工業園.為盡量減少耕地占用,問:如何確定B點的位置,使得該工業園區的面積最小?并求最小面積.
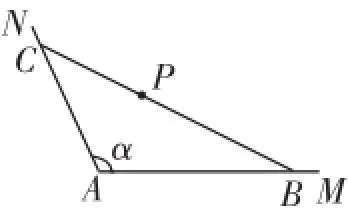
圖1
二、命題意圖
學生在學習直線與圓時,曾經做過這樣的題目:“在直角坐標系xOy中,已知點P(1,3),過點P作一直線l交x軸于點B,交y軸于點C,求△OBC的面積的最小值.”當初學生有三種解法,法1是設斜率k,求出B、C兩點的坐標,然后利用直角三角形的面積建立k為變量的函數;法2是設截距式,然后用基本不等式求解;法3是連接OP,把三角形的面積分割成△OBP、△OCP的面積和來求解.為了給高二出一道月考的應用題,決定把上面的原題改編成應用題,另外學生剛剛學習了橢圓,為了考查學生用解析法解題的首要任務就是建立恰當的直角坐標系,所以將y軸繞原點旋轉變成y=-2x,為了增加建系的難度,特意將O點改為A點,看看學生是否會選A點為坐標原點.
三、參考答案
解:如圖2,以A為原點,AB為x軸,建立平面直角坐標系.…2分
因為tanα=-2,故直線AN的方程是y=-2x.
設點P(x0,y0).因為點P到AM的距離為3,故y0=3.
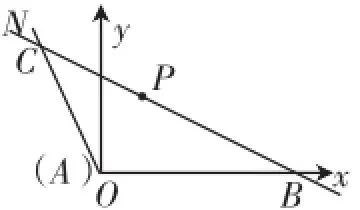
圖2
所以點P(1,3).…4分
顯然直線BC的斜率存在.設直線BC的方程為y-3= k(x-1),k∈(-2,0).
從而S有最小值15.
答:當AB=5km時,該工業園區的面積最小,最小面積為15km2.…16分
四、考試結果
全校900多人參加考試,從閱卷的情況來看,平均分為5.15分,12%的學生能完全做對,25%的學生建系不對,30%的學生不會求分式函數的最值,大大出乎筆者的意料.究其原因,主要存在以下幾個問題.
1.不會建模
受推導橢圓標準方程建系的影響,有15%的學生以AB所在直線為x軸,其中垂線為y軸來建系,因為AB的長度在變化,這樣建系的同學就全軍覆沒了.還有10%的學生以CB所在直線為x軸,點P為坐標原點來建系,同樣是CB的長度在改變,不容易求解.
2.忽視直線BC的斜率的取值范圍
因為要使直線BC與AM的交點在第二象限,斜率k必須滿足k∈(-2,0),若定義域都忽視了,方法哪怕正確結果也會出錯.
3.不會解模
讓人眼睛一亮的地方是學生有好幾種解法.法1:(求導)目標函數建立如同參考答案.
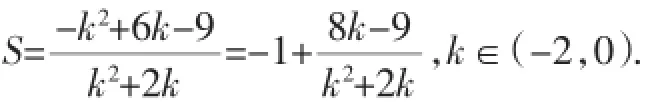
以下同參考答案.
法2:(二次函數)目標函數建立如同參考答案.時,S取得最小值15.
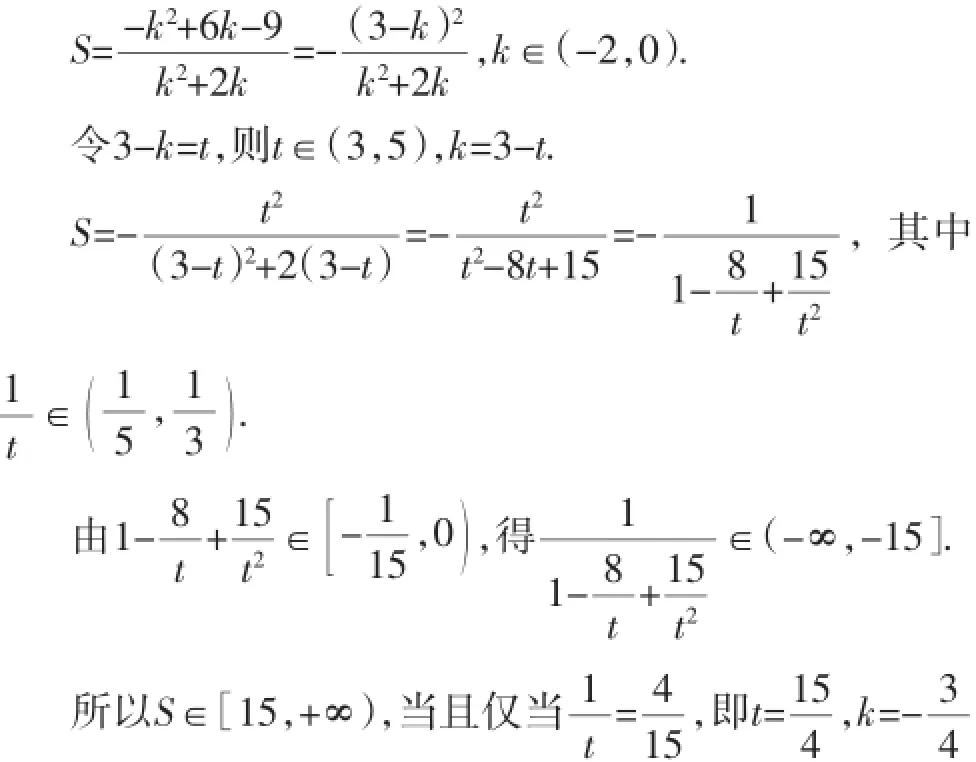
以下同參考答案.
法3:(方程有解)目標函數建立如同參考答案.
(1)在(-2,0)上有一解.
由f(0)=9>0,得f(-2)<0,但f(-2)=25>0,應舍去.
(2)在(-2,0)上有兩解.
以下同參考答案.
法4:(基本不等式).
如圖3,過點P作PE⊥AM,PF⊥AN,垂足分別為E、F,連接PA.設AB=x,AC=y(x>0,y>0).因為P到AM、AN的距離分別為3、,所以PE=3,PF=
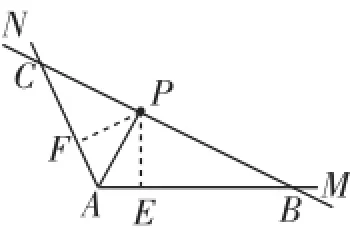
圖3
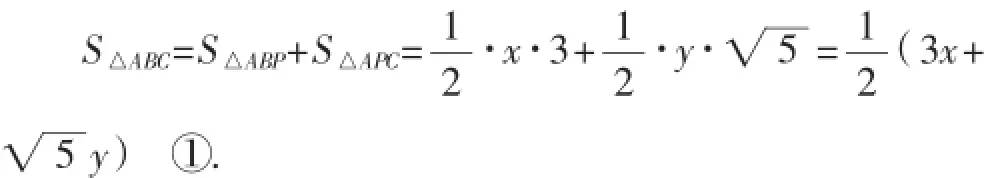

下同法4.
法6:(幾何法尋求約束條件).
如圖2,以A為原點,AB為x軸,建立平面直角坐標系.設AB=m,AC=n(m>0,n>0).用參考答案的方法求得P(1,3).
下同法4.
盡管解法很多,但本質只有兩種.一是用解析法求面積的目標函數,轉化為求二次比二次型的分式函數最值,法1和法2是通法,法3不具有一般性,法4、法5較難想到.二是利用等面積法轉化為求多變量的最值.法6恰好采用解析法建模,然后轉化為求兩個變量的最值,可以消元來解,也可以利用基本不等式或柯西不等式來求解.
五、幾點思考
1.本題的難點之一在于建系
實際上用解析法解題的基礎就是如何建立適當的直角坐標系,適當兩字看似簡單,運用起來還是有講究的.很多學生受推導橢圓標準方程建系的影響,關鍵是沒理解橢圓的兩個焦點是定點,而這里的A、B兩點中B是運動變化的,因此在教學時如果我們能適時地強調兩者的區別,那么學生犯這樣的錯誤的機率就小了.
2.本題的難點之二在于解模
3.本題的易錯點在于忽視k的取值范圍
范圍問題是老大難的問題,為此我們要讓學生明白檢驗的重要性,既要檢驗所得結果是否適合數學模型,又要評判所得結果是否符合實際問題的要求.
總之,將實際問題抽象為數學問題時,要讀懂題目,建立數學模型,選擇合適的方法,設計合理、簡捷的運算途徑,這樣求出數學問題的解就不難啦!A

