《解后思，思什么？》的再思考

☉吉林省延邊第二中學 張孝梅

《解后思，思什么？》的再思考

☉吉林省延邊第二中學 張孝梅

文1從審題過程、解題過程、解題方法、一題多解四個方面系統(tǒng)地闡述了解題后進行反思，可以收到事半功倍的效果.拜讀文章以后，還有一種余興未盡的感覺.由長期的教學實踐感覺到：解題后如果能從問題的本質、規(guī)律的探究、數(shù)學思想的整合等方面進一步反思、探索，學生的思維可以在解題后繼續(xù)飛翔，更是一件錦上添花的事.本文結合教學實踐中的解題案例，續(xù)談對《解后思，思什么？》的再思考.

一、反思問題的本質——挖掘思維潛能

解題后，在了解知識結構的基礎上，能否對其中所蘊含的問題的本質進行深入的探究？能否把問題所蘊含的孤立的知識“點”，擴展到系統(tǒng)的知識“面”？通過進一步地探索，學生可以在系統(tǒng)化的知識結構中發(fā)現(xiàn)解決問題的本質特征，進一步挖掘出學生思維的潛能.

解析：由①知函數(shù)（fx）的圖像關于直線x=1對稱，由②知函數(shù)f（x）的周期為4，由③知函數(shù)f（x）在［1，3］上單調遞減，所以容易得到f（2014）=f（2），f（2015）=f（3），f（2016）=f（4）=f（0）=f（2），由圖像選出正確答案C.

反思：圖像是幫助解決問題的有力工具，而對于此題在畫圖像時學生感到最大的障礙就是面對①和②兩個等式，如何區(qū)別周期和對稱性，若能夠迅速辨析等式的本質特征，問題可迎刃而解.解題后進一步引導學生思考、探究：在常見的抽象函數(shù)等式中，你能發(fā)現(xiàn)關于周期和對稱性問題的本質特征嗎？學生的思維潛能是無限的，只要善于挖掘，就一定有收獲.

二、反思解題規(guī)律——實現(xiàn)思維遷移

對于某一具體問題的解答往往不是困難的事，感覺困難的是能否對一類問題進行尋根問底，探索其一般性的結果，能否嘗試、發(fā)現(xiàn)其規(guī)律性的東西.如果能夠形成自己獨到的見解，盡管是點滴的小發(fā)現(xiàn)，都能喚起學生的成就感.長期積累成自然，更有利于促進學生良好的學習習慣，實現(xiàn)學生有效思維的遷移.

例2數(shù)列｛an｝滿足a1=2，an+1=2an+2，求數(shù)列｛an｝的通項公式.

解析：觀察遞推公式的結構特征，并進行變形：an+1+ 2=2（an+2），由此，將問題化歸為：數(shù)列｛an+2｝是一個以4為首項、以2為公比的等比數(shù)列，易得an=2n+1-2.

變式1：數(shù)列｛an｝滿足a1=1.

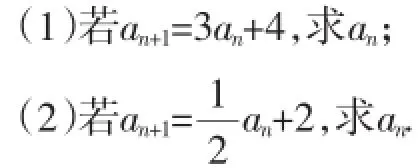
變式2：數(shù)列｛an｝滿足an+1=pan+q（p≠1），求數(shù)列｛an｝的通項公式.

反思：以上問題的結構有什么共同特征？如何將數(shù)列化歸為等比數(shù)列？能夠發(fā)現(xiàn)一般性的規(guī)律嗎？學生借鑒前面成功的經(jīng)驗，分析式子的特點，將原式變形為an+1+數(shù)列｛an+t｝是以a1+t為首項、p為公比的等比數(shù)列，進而得到數(shù)列｛an｝的通項公式an.學生在自我探索的過程中，明白了用待定系數(shù)法構造新的等比數(shù)列的一般性規(guī)律，其中t的值自然也就不用死記硬背了.

三、反思數(shù)學思想——提煉思維精髓

數(shù)學思想是數(shù)學的靈魂，可以說，“知識”是基礎，“方法”是手段，“思想”是精髓，提高數(shù)學素質的核心就是提高學生對數(shù)學思想方法的認識和運用.因此，解題后如果能夠在深入探討知識間的聯(lián)系，反思一類問題通用解法的基礎上，有意識地引導學生挖掘數(shù)學知識本身所蘊含的數(shù)學思想，更有利于提煉學生思維的精髓.

例3如圖1，正三棱柱ABC-A1B1C1的底面邊長為a，側棱長為a，D1為A1C1的中點.

（1）求證：BC1∥平面AB1D1；

（2）求證：平面AB1D1⊥平面AA1C1C.

解析：（1）方法1：依據(jù)線面平行的判定定理，證出D1E∥BC1（E為AB1的中點），從而得出結論；

方法2：依據(jù)面面平行的性質，構造平面BC1D∥平面AB1D1，得出結論.

（2）依據(jù)面面垂直的判定定理，由正三棱柱證得B1D1⊥平面AA1C1C，進而證得平面AB1D1⊥平面AA1C1C.

反思：此題為直線與平面關系中關于平行與垂直的論證問題，突出體現(xiàn)了化歸與轉化的數(shù)學思想（圖2為直線與直線、直線與平面、平面與平面垂直轉化的結構框架），但學生愿意以題解題，而不習慣對其數(shù)學思想進行提煉，事實上學生在解題的同時，注重規(guī)律方法的總結和數(shù)學思想的滲透，是訓練學生學會解題的有效途徑，更是提煉思維精髓的體現(xiàn).

圖1

圖2

著名數(shù)學教育家波利亞說過：“數(shù)學問題的解決僅僅只是一半，更重要的是解題之后的回顧”.所謂回顧，即我們現(xiàn)在說的反思.總之，解題后注重反思、善于反思，既可促進“雙基”的掌握，又能加強知識的有效遷移，有利于培養(yǎng)學生良好的思維品質，是提高解題能力、學好數(shù)學、用好數(shù)學的重要途徑.

1.成雪蘭.解后思，思什么？［J］.中學數(shù)學（上），2010（12）.A