讓學生擔當課堂的主角

☉內蒙古赤峰市赤峰二中 郭桂玲

讓學生擔當課堂的主角

☉內蒙古赤峰市赤峰二中 郭桂玲

新課程倡導教師積極轉變教與學的方式，把主動權還給學生，教師應是學生發展的促進者，是學生學習的組織者、引導者、參與者和欣賞者.教師在充分放手讓學生思考的基礎上，又能準確啟發指導.本文以“點到直線的距離”的教學為例說明.

一、教學設計思路

“點到直線的距離”是“坐標平面上的直線”一章的最后一節內容.我們希望找到一種教學方案，既滲透解析法的方程思想，又體會向量方法的便捷性，我們決定將問題交給學生，放手讓學生去探究“如何求點到直線間的距離”這個問題.我們希望通過教學，幫助學生學會推導點到直線的距離公式，并掌握點到直線的距離公式；通過對點到直線間距離公式推導方法的分析、比較與體驗，引導學生領悟公式推導過程中的數學思想和思維方法，培養學生分析問題和解決問題的能力.在教學過程中，點到直線的距離公式及其推導過程是教學重點；如何引導學生學習和領悟對問題的思維過程及所蘊含的教學思想方法，這應該是教學的難點.

二、教學設計過程

1.引入

通過師生對話問答回顧知識，將知識結構化，形成以下知識結構.

圖1

說明：引入中，從學生原有的知識基礎出發，通過知識的邏輯結構說明為什么學習點到直線的距離，激發學生學習的興趣，強調理性思維.

圖2

2.點到直線的距離公式的推導

（1）明確并提出問題.

如圖2，已知直線l∶Ax+By+C=0，直線外一點P（x0，y0），其中A、B、C、x0、y0為常數，如何表示點P到直線l的距離d？

在解決該問題前可以作如下鋪墊.

師：什么是點到直線的距離？P到l的距離是一個確定的值嗎？如何求點P（x0，y0）到直線l：Ax+By+C=0的距離？

師：作PQ⊥l于Q，如何計算線段PQ的長度？你能想到哪些方法？（同學們思考討論）

說明：這里先回顧“什么是點到直線的距離？”從幾何角度作出距離|PQ|，并指出點到直線的距離其實是點到直線上任意一點的距離的最小值.再指出點P到直線的距離是一個確定的值，它可以用常數x0、y0、A、B、C表示.最后引導學生思考問題的解決途徑，進入討論.

（2）推導點到直線的距離公式.

通過對問題的初步分析，我們將”求點到直線之間的距離”歸結為“如何計算線段PQ的長度？”因為求線段長的方法有許多種，所以可以先由學生充分探索，再通過合理有效的組織，引導學生掌握方法的本源，尋找問題的解決方法.

①充分引導學生自主探索，展現問題解決的思維過程.

生1：計算Q點的坐標.

師：為什么想到求Q點的坐標？如何計算Q點的坐標？生1：有下列兩種方法.

（1）解聯立方程組，寫出直線PQ的方程，聯立PQ與l的方程，求解Q點的坐標（x1，y1）.

（2）利用數量積計算Q點的坐標，設Q（x1，y1）

師：這種方法是一定可以做到底的，就是不知道解方程會不會給我們帶來麻煩.先放一下，其他同學還有其他方法嗎？

生2：為避免求Q點的坐標，可用面積相等.（示意想到黑板上作圖說明）

生2：利用三角形面積公式可知|PQ|·|RS|=|PR|·|PS|，從而可求|PQ|.

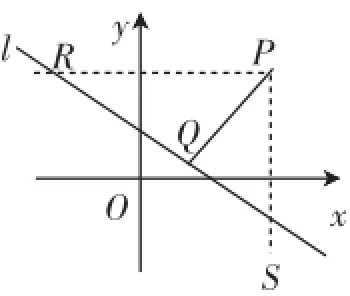
圖3

生3：用向量的數量積.

師：為什么會想到數量積？

師：這個方法值得一試，設想一下它后續的一些步驟，可能會遇到什么問題？M點的坐標需要代換，如何代換？注意點M在直線上，能否得出結果，我們待會可以嘗試一下.

師：還有其他方法嗎？

學生又提出了利用三角比、勾股定理等平面幾何知識，利用函數思想求距離的最小值等方法.

②合理選擇解題方法，突出方程思想與向量方法.

師：所有這些都可以試一試，現在，我們選擇兩種典型的、有代表性的，也是有一般意義的方法：（1）用生2的方法解聯立方程組，看看能否算出|PQ|的長度；（2）向量方法是一個重要的解決問題的方法，試一試能否用向量的數量積將|PQ|的長度算出來？

（學生分組討論，派代表到黑板上板演）

生4：由P（x0，y0），可設R（x1，y0），S（x0，y2）.又R、S在直

師：這個方法的關鍵是什么？

生4：利用了方程思想和整體代換思想.

師：好，我們再看用向量方法計算出|PQ|.

師；在這個方法中，你們認為關鍵是什么？

生：數量積及在直線上的點的坐標滿足直線方程.

③回顧反思兩種方法，體驗其中的數學思想.

師：剛才我們用解析幾何中兩種典型的方法計算出：點P（x0，y0）到直線l：Ax+By+C=0的距離d.雖然方法有許多種，但是因為解析幾何的核心思想是利用方程研究曲線，所以解聯立方程組是基本方法，又因為向量在解析幾何中是一個重要的知識和方法，計算簡潔，體現了向量方法的優勢，值得我們細細體會.

三、公式的應用

師：現在你們能推導兩條平行線之間的距離公式嗎？

問題：若直線l1：Ax+By+C1=0，l2：Ax+By+C2=0，其中A、B、C1、C2為常數，且C1≠C2，如何求l1與l2的距離？

這個問題由學生獨立解決，教師主要是引導并介紹方法.

生6：利用點到直線的距離（轉化為求點到直線間的距離）.

在直線l1上取點P（x0，y0），則

由Ax0+By0+C1=0，得Ax0+By0=-C1，所

師：還有沒有其他方法？

生7：也可以用向量的數量積（直接利用向量方法求距離）.

師：這個式子可作為公式使用，但要注意A、B的一致性.

在新課標的要求下，我們要充分發揮學生的主觀能動性，在突出學生自主學習的基礎上，教師作適當引導.教師要善于捕捉來自于學生的智慧和火花，敢于采納學生的點子和方案，這樣有利于充分調動學生的積極性、主動性，有利于增強學生的自信心.給學生一個寬廣的舞臺吧，讓學生擔當課堂的主角，讓他們的思維激情燃燒.

1.普通高中數學課程標準（實驗）解讀［M］.南京：江蘇教育出版社，2004.

2.方國才.新課程怎樣教得精彩［M］.北京：中國科學技術出版社，2006.A